Lezione 1

Il metodo degli elementi finiti, in generale, fornisce una soluzione approssimata derivante dalla discretizzazione del sistema di equazioni differenziali che descrive il comportamento del componente in esame. Un’applicazione di questo metodo è quello di verifica strutturale. Il caso qui presentato è l’analisi di un dente di una ruota dentata che viene considerato isolato dal resto della ruota stessa. Analizziamo i fenomeni che avvengono localmente nel raccordo con il corpo della ruota, nel caso in cui il dente sia sottoposto a un carico P come in Figura 1.

Il dente è schematizzato in 2D e P rappresenta la risultante delle pressioni di contatto con il dente reciproco dell’altra ruota. L’intento è quello di studiare lo stato tensionale di questa porzione locale di struttura. Viene dunque definito un dominio elastico (al più elasto-plastico) continuo, cioè quella porzione di spazio occupata dal materiale costituente il dente che si comporta secondo leggi elastiche nella deformazione. È possibile studiare il fenomeno tramite equazioni differenziali “completate” con le opportune condizioni al contorno (cioè le condizioni che devono essere rispettate sul bordo del dente (dominio) considerato). Esistono anche forze che agiscono dall’interno del dominio (ad esempio: forza di gravità, inerzia, ecc..), ai fini della risoluzione dell’equazione differenziale consideriamo anch’esse condizioni a contorno. I carichi entrano nella struttura e in prossimità dello strappo. In questo caso per avere equilibrio agli spostamenti della struttura si considera un incastro (in questo modo al dente viene come assegnata una posizione nello spazio). I punti appartenenti allo strappo dunque hanno spostamento e rotazione nulli. Possiamo quindi ricavare le equazioni differenziali, ma la loro soluzione non é facilmente determinabile a causa della complessità geometrica del problema. Una soluzione è quella di discretizzare il problema, ad esempio immaginandolo composto da aste (figura1.b), ma questo sottostimerebbe la rigidezza dell’elemento.

Per la trattazione di un corpo continuo si procede analizzando una porzione infinitesima di materiale considerata per semplicità di forma cubica. Il cubo sarà caratterizzato da un suo stato tensionale che dipende ovviamente da quello globale dell’elemento considerato (in questo caso il dente). Lo stato tensionale è rappresentabile, una volta definito il sistema di assi cartesiani xyz, tramite le componenti (normali e tangenziali) di tensione che agiscono sulle facce del cubetto infinitesimo.

TODO: inserire immagine cubetto con tutte e 6 (o 9) le componenti di tensione

sorgente ipe

Consideriamo il punto P di coordinate (x,y,z), e da questo costruiamo un cubo di dimensioni dx,dy,dz. Consideriamo la faccia che si sviluppa parallela al piano yz, con normale x (il procedimento sarà uguale per le altre facce). Si osserva che l’equilibrio alla rotazione intorno ai tre assi implica la simmetria delle tensioni tangenziali $\tau$ .

$$ \begin{cases} & \tau_{xy} = \tau_{yx}\\ &\tau_ {xz}=\tau_ {zx}\\ &\tau_ {yz}=\tau_ {zy} \end{cases} $$

Sulla faccia parallela al piano yz contenente P agisce $\sigma{x}$, se ci spostiamo di dx ,sulla faccia opposta agisce $\sigma{(x+dx)}$ , che calcoleremo approssimando tramite la serie di Taylor troncata al primo ordine. Imponendo dunque l'equilibrio in direzione x otteniamo:

$$ \frac{ \partial \sigma_x }{ \partial x } + \frac{ \partial \tau_{xy} }{ \partial y } + \frac{ \partial \tau_{zx} }{ \partial z } + q_x =0 $$

ove $q_{x}$ è un carico distribuito per unità di volume orientato in direzione $x$.

Analogamente, facendo lo stesso ragionamento lungo le direzioni y e z, otteniamo la seconda e la terza equazione di equilibrio:

$$ \frac{ \partial \tau_{xy} }{ \partial x } + \frac{ \partial \sigma_y }{ \partial y } + \frac{ \partial \tau_{yz} }{ \partial z } + q_y =0 $$

$$ \frac{ \partial \tau_{zx} }{ \partial x } + \frac{ \partial \tau_{yz} }{ \partial y } + \frac{ \partial \sigma_z }{ \partial z } + q_z =0 $$

Consideriamo adesso le equazioni di compatibilità cinematica che imporranno l’assenza di “strappi” nel materiale. Queste devono essere scritte in funzione degli spostamenti, in modo da rispettare le equazioni di continuità. Posto u lo spostamento lungo x e v, w rispettivamente gli spostamenti lungo y e z ottengo:

$$ \begin{cases} \epsilon_{x}=\frac{\partial u}{\partial x},\\ \epsilon_{y}=\frac{\partial v}{\partial y},\\ \epsilon_{z}=\frac{\partial w}{\partial z},\\ \gamma_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x},\\ \gamma_{zy}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z},\\\gamma_{xy}=\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x},\\\end{cases} $$

u, v, w sono funzioni continue sul dominio elastico. Scrivendo la relazione tra le deformazioni e gli spostamenti, si limitano i possibili stati deformativi a quelli che rispettano la compatibilità. Dobbiamo infine trovare un legame tra σ ed ε che, per un materiale isotropo (come tutti quelli che, sotto ipotesi semplificativa, prenderemo in considerazione) risulta di tipo lineare. Il legame tensione-deformazione segue la legge di Hooke : il vettore delle tensioni agenti sono uguali al vettore degli spostamenti premoltiplicato per la matrice di legame elastico $$ \def\X{\frac{E\left(1-\nu\right)}{\left(1-2\nu\right)\left(1+\nu\right)}} \def\Y{\frac{E\nu }{\left(1-2\nu\right)\left(1+\nu\right)}} \begin{bmatrix} \sigma_{x}\\ \sigma_{y}\\ \sigma_{z}\\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{bmatrix} = \begin{bmatrix} \X&\Y&\Y&0&0&0 \\ \Y&\X&\Y&0&0&0 \\ \Y&\Y&\X&0&0&0 \\ 0 &0 &0 &G&0&0 \\ 0 &0 &0 &0&G&0 \\ 0 &0 &0 &0&0&G \end{bmatrix} \begin{bmatrix} \epsilon_{x}\\ \epsilon_{y}\\ \epsilon_{z}\\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{bmatrix} $$

È possibile scrivere anche l’operazione inversa, premoltiplicando il vettore delle tensioni per l’inversa della matrice di legame elastico. Gli zeri presenti in entrambe le matrici evidenziano l’assenza di legami tra le σ e le ε e tra le τ e le .

$$ \def\X{\frac{1} {E}} \def\Y{\frac{-\nu}{E}} \def\Z{\frac{1} {G}} \begin{bmatrix} \epsilon_{x}\\ \epsilon_{y}\\ \epsilon_{z}\\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{bmatrix} = \begin{bmatrix} \X&\Y&\Y&0&0&0 \\ \Y&\X&\Y&0&0&0 \\ \Y&\Y&\X&0&0&0 \\ 0 &0 &0 &\Z&0&0 \\ 0 &0 &0 &0&\Z&0 \\ 0 &0 &0 &0&0&\Z \end{bmatrix} \begin{bmatrix} \sigma_{x}\\ \sigma_{y}\\ \sigma_{z}\\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{bmatrix} $$

Le equazioni di legame, insieme con le condizioni al contorno, permettono di risolvere, in via teorica, qualsiasi problema di tipo strutturale, ma per geometrie e carichi non elementari, le equazioni non sono di facile risoluzione, si adotta perciò il metodo degli elementi finiti, che opera una discretizzazione del continuo.

Riconsiderando il dente della ruota dentata, ad esempio, possiamo adottare una discretizzazione del tipo (caso 2D) In cui il dominio viene suddiviso in sottodomini come in figura. Assunta quindi l’ipotesi di comportamento cinematicamente semplice (supponendo quindi un campo di spostamenti lineare dei punti). 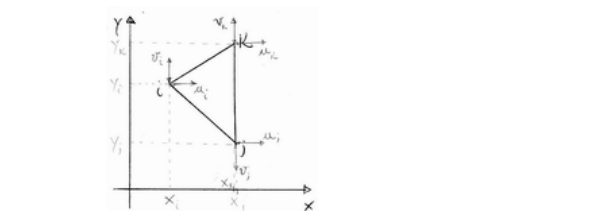Imponiamo che la relazione valga con continuità fino ai vertici, per cui deve essere che:

$$ \begin{cases} & u_{i} = \alpha_{1}+\alpha_{2}x+\alpha_{3}y\\ & v_{i} = \alpha_{4}+\alpha_{5}x+\alpha_{6}y\\ &u_{j} = \alpha_{1}+\alpha_{2}x+\alpha_{3}y\\ & v_{j} = \alpha_{4}+\alpha_{5}x+\alpha_{6}y\\ &u_{k} = \alpha_{1}+\alpha_{2}x+\alpha_{3}y\\ & v_{k} = \alpha_{4}+\alpha_{5}x+\alpha_{6}y\\ &\end{cases} $$ Essendo le equazioni degli spostamenti u e v disaccoppiate, possiamo anche analizzare separatamente gli spostamenti lungo le due direzioni (x e y), ottenendo due sistemi distinti. Considerato ad esempio il sistema descrittivo degli spostamenti lungo x, ottengo $$ \begin{cases} & u_{i} = \alpha_{1}+\alpha_{2}x+\alpha_{3}y\\ &u_{j} = \alpha_{1}+\alpha_{2}x+\alpha_{3}y\\ &u_{k} = \alpha_{1}+\alpha_{2}x+\alpha_{3}y\\ &\end{cases} $$ Un sistema di tre equazioni nelle tre incognite a1,a2 e a3 risolvibile col metodo di Cramer

Possiamo quindi ricavare α1 , α2 , α3 in funzione dei tre spostamenti nodali dell'elemento triangolare. Considerato un punto generico P interno all’elemento finito, il suo spostamento sarà uguale ad una media pesata degli spostamenti dei tre nodi, dove i pesi saranno le aree racchiuse dalle congiungenti i vertici col punto P. 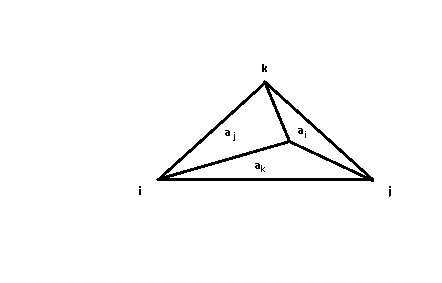L’area totale del triangolo sarà: $ a=a_i+a_j+a_k $
dunque per il P considerato, lo spostamento sarà pari a: $$ u(x,y)=u_{i}\frac{a_{i}}{a}+u_{j}\frac{a_{j}}{a}+u_{k}\frac{a_{k}}{a} $$ $$ v(x,y)=v_{i}\frac{a_{i}}{a}+v_{j}\frac{a_{j}}{a}+v_{k}\frac{a_{k}}{a} $$ Dove a, area del triangolo, sarà facilmente determinabile con la formula: $$ a=\begin{vmatrix} 1 &1 &1 \\ x_{i} & x_{j} &x_{k} \\ y_{i} & y _{j} &y _{k} \end{vmatrix}\frac{1}{2!} $$ dove “2” indica il numero di dimensioni nello spazio.

Per trovare il volume del tetraedro nelle 3 dimensioni spaziali si procede con: $$ V=\begin{vmatrix} 1 & 1 &1 &1 \\ x_{i }& x_{j} & x_{k} &x_{h} \\ y_{i} & y_{j} & y_{k} &y_{h} \\ z_{i} & z_{j} &z_{k} & z_{h} \end{vmatrix}\frac{1}{3!} $$

Si riassumono i seguenti punti chiave che descrivono la teoria degli elementi finiti:

1. Discretizzazione della struttura inizialmente continua, operazione comunemente definita meshatura o discretizzazione;
2. In funzione degli spostamenti nodali, che sono considerati come incognite primarie, si calcolano tutte le grandezze di interesse (ad. es. le forze);
3. Per valutare tali forze occorre calcolare le deformazioni (che si ottengono differenziando gli spostamenti), poi le tensioni (impiegando la legge di Hooke ad un materiale elastico lineare isotropo) ed infine, tramite un approccio energetico, calcolare dalle tensioni le forze che il singolo elemento esercita ai vertici