Lezione 5: wxMaxima: Integrazione definita, ossia Quadratura gaussiana

In questa lezione abbiamo analizzato, con l'ausilio di alcuni esercizi, l'approssimazione di integrali definiti di funzioni generiche attraverso la Quadratura di Gauss ad uno e due punti, l’approssimazione di funzioni semplici con Taylor ed altri costrutti per iniziare ad approfondire l'utilizzo del wxMaxima.

Sono stati introdotti nuovi comandi per un utilizzo più efficace del manipolatore algebrico.

Con questo comando è possibile definire una funzione. La funzione richiede di esplicitare dei parametri, ad esempio:

f(x) : x è semplicemente un segnaposto, dove il primo parametro passato alla funzione verrà sostituito ovunque trovi x dentro l’espressione.

Nel caso si avessero più parametri, questi vengono separati da delle virgole.

define 

Questo comando permette di definire le funzioni con la valutazione all’atto della definizione e non all’atto della chiamata.
Perciò, se scrivo

a0:0
f(x):= a0 + a1*x

il programma mi fornisce come output a0 + a1x.
Ma se invece digito

define (f(x), a0 + a1*x)

allora il manipolatore scrive a1x, poichè compie subito la valutazione.

expand

Permette di espandere la funzione in somma di monomi e ne effettua la semplificazione.

[…. , ….] 

Si tratta del comando lista. Se si vuole avere un sistema di equazioni all’interno del manipolatore si crea una lista di equazioni, dove ogni equazione è separata da una virgola.
In generale una lista può contenere qualunque entità, anche altre liste.

 (…)

Le parentesi tonde, a differenza delle quadre, denotano un blocco.

Per creare un ciclo di lista invece si deve creare un costrutto do

Il ciclo for permette di ripetere una data operazione più volte.

 length

Estrae la lunghezza della lista in esame, e il ciclo for costruisce un polinomio in cui la x è elevata a ciascuno dei termini della lista creata in precedenza. La lunghezza della lista è il numero degli elementi.

wxplot2d 

Permette di plottare la funzione, ovvero graficarla. Con wx si indica che la figura è di tipo statico, ovvero che viene rappresentata sulla stessa interfaccia.
Viene scritta in questo modo:

wxplot2d ([funzione 1, funzione 2] [variabile, inizio intervallo, fine intervallo])

ATTENZIONE: non posso plottare una funzione che contiene parametri senza averli prima definiti

 plot2d 

Permette di plottare la funzione in una nuova finestra, fuori dal foglio di lavoro.

 plot3d 

Permette di plottare la funzione lungo le 3 dimensioni.

  limit 

Svolge l’operazione di limite.

es) limit (f(x), x, inf)

 inf 

Rappresenta un infinito reale positivo.

  append

Questo è il comando che permette di accodare una funzione ad un’altra funzione.

  makelist 

Si tratta del comando per la costruzione automatica di funzioni di lista. Crea una lista scorrendo un indice i.

Un esempio è:

questo codice può essere copiaincollato da/a wxmaxima o fortran

 taylor  

Permette di effettuare l’espansione in serie di Taylor.

Un classico esempio generico sarebbe:

 legend 

È la parola chiave che permette di creare una legenda. Può ritornare utile impostare manualmente la legenda, creando una lista sul manipolatore algebrico.

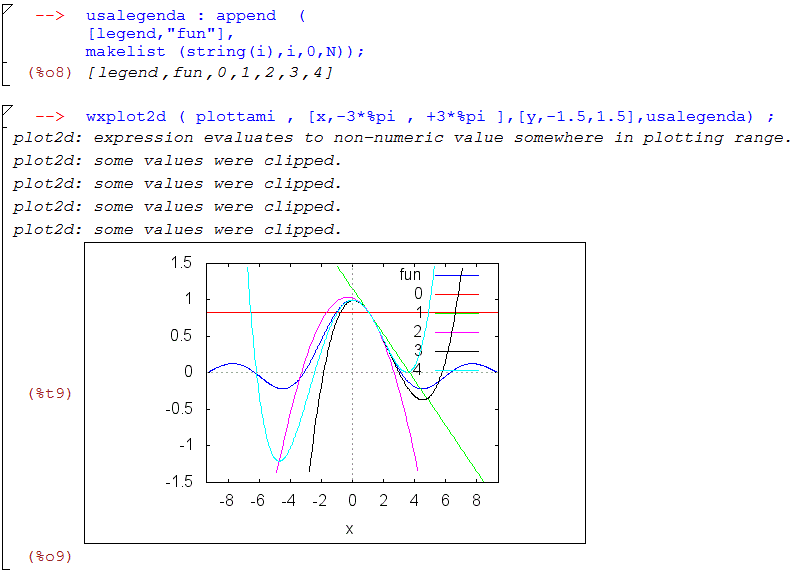
Per convertire in una legenda un numero (ad esempio 1) in una stringa utile per la legenda si usa il comando di conversione in stringa denominato string.

 quad-qag 

È una funzione di libreria che permette di effettuare l’integrale in forma numerica con il metodo dei trapezi.

Col termine quadratura si intende un'integrazione numerica di integrali, impiegata quando non li si riesce a calcolare in forma analitica. Si tratta di una forma numerica approssimata per calcolare rapidamente gli integrali di funzione.

La quadratura gaussiana è una stima; non è una delle soluzioni più precise, salvo aumentando i punti di campionamento, ma è molto rapida ed è sempre usata nei codici agli elementi finiti.

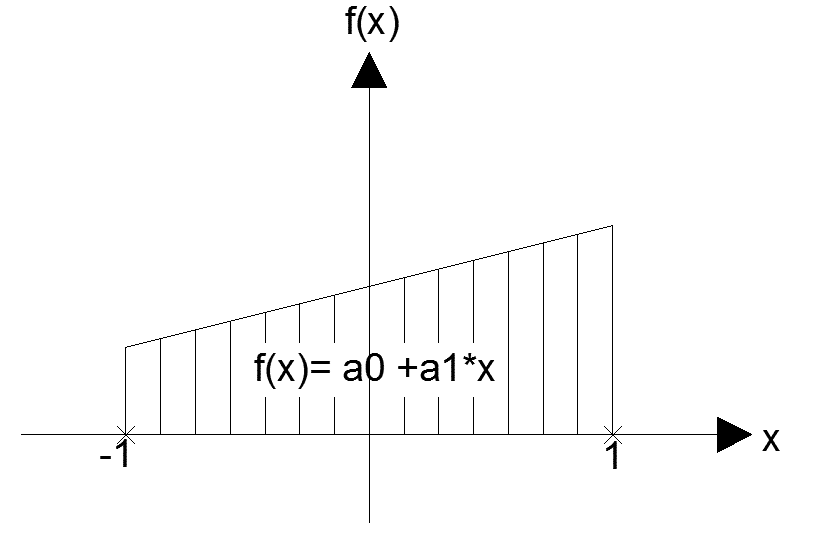
Si supponga di voler risolvere l’integrale normalizzato su un intervallo [-1,1] (dunque simmetrico rispetto all'origine) di una funzione generica f(x) mediante il metodo della quadratura gaussiana (ovvero il campionamento della funzione). Occorre definire innanzitutto un numero n di punti di campionamento xi, lungo l'asse x, ai quali vanno associati biunivocamente i pesi wi. La somma dei pesi è sempre 2.
L’integrale sarà risolto come somma pesata dei contributi f(xi):

$$ G = \sum_{i=1}^n w_i f(x_i) $$

La scelta dei punti è totalmente arbitraria, ma se vengono usati i punti di Gauss si ottiene la stima migliore, ovvero l'errore minimo nel calcolo dell'integrale. Il seguente esercizio serve a mostrare ciò.

Si pensi alla funzione campione:

f(x)=a0+a1*x con a0 e a1 costanti qualsiasi

e si immagini di volerla integrare fissato un punto x1 sull’ asse delle ascisse e un relativo peso w1.

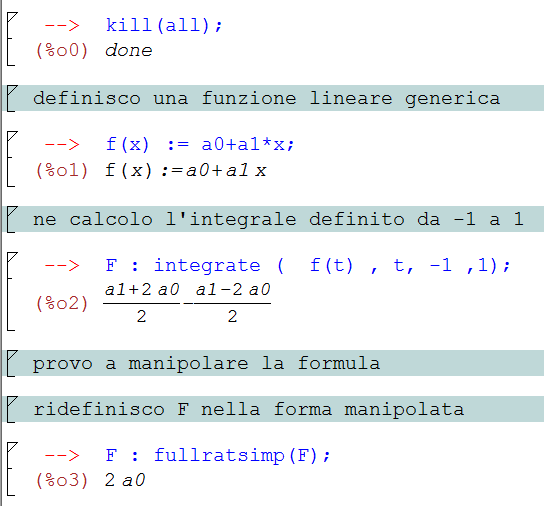
L’ implementazione attraverso il programma MAXIMA avverrà nel seguente modo:

proseguendo con l’ algoritmo risolutivo non resta che calcolare G (cioè il risultato della nostra sommatoria), assegnare un errore al campionamento sotto forma di residuo e trovare due soluzioni costanti in a0 e a1 che rendano costante il residuo senza annullarlo. In altri termini, si vuole che il residuo dipenda solo da x1 (e w1) e non da a0 e a1.
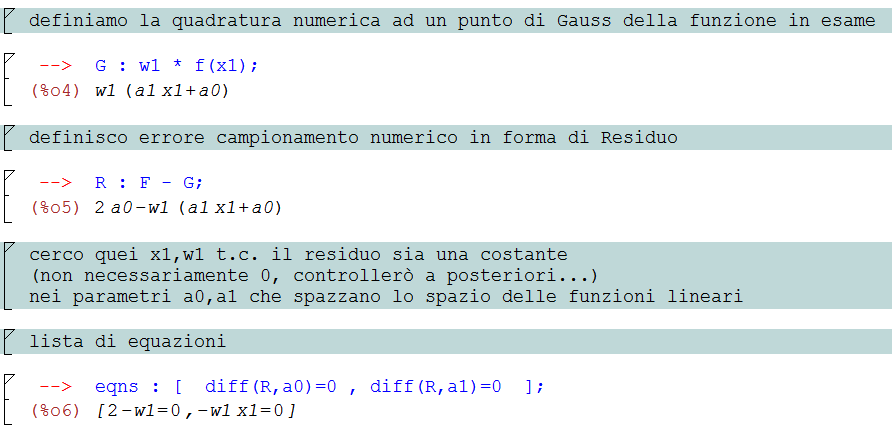
Implementando:

si noti che nel residuo sono presenti le variabili x1 w1 a0 a1 contemporaneamente. Sarà necessario inserire una lista di equazioni da risolvere in una apposita lista di incognite:

le equazioni sono state risolte attraverso la funzione ‘solve’ (e non ‘globalsolve’) a causa della non linearità del sistema (dovuta al termine –w1*x1) ; a posteriori è stato effettuato un controllo della soluzione al fine di non annullare il residuo.

È possibile scrivere allo stesso modo un’integrazione a due punti. Così si avranno due pesi per i due punti: x1, w1, x2, w2, ovvero si hanno 4 incognite in 4 equazioni.

Si parte da una funzione polinomiale che abbia 4 coefficienti su cui fare le derivate del residuo, perciò nel caso specifico sarà una funzione cubica.

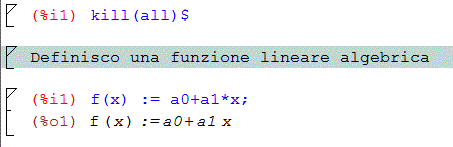
Relegando il calcolo ai manipolatori algebrici si ha:

Il polinomio parallelo, secondo Gauss vale:

Si indaga nel seguito per quali scelte dei punti xi e dei pesi wi l’eguaglianza precedente valga esattamente, e si impone che il residuo R si annulli.
Siccome la precedente eguaglianza deve valere per valori generici dei coefficienti “ai” del polinomio f, tale eguaglianza deve rimanere valida anche per variazioni di tali coefficienti, il che si esprime annullando la derivata del residuo rispetto ai coefficienti “ai”:

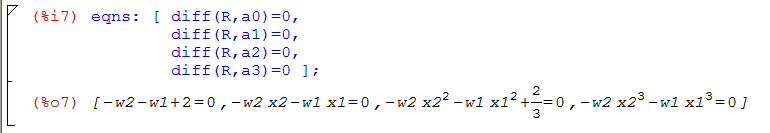
dove tali equazioni devono essere associate all’equazione iniziale.

Definite le incognite che risolvono le equazioni e combinando le equazioni stesse si ottengono i valori delle incognite.

Si verifica con facilità che l’equazione iniziale R=0 viene soddisfatta dalla scelta dei due pesi w1 e w2 e dei due punti di Gauss x1 e x2.

In generale, la quadratura gaussiana prevede lo stesso approccio per n punti, e integra esattamente un polinomio di grado 2n-1.
I polinomi di gradi diversi da questi valori possono essere considerati casi particolari di quelli di grado superiore, per cui vengono integrati con il tipo di quadratura adatto a questi ultimi.
es) 2 punti: polinomio di grado 3; quello di secondo grado è un caso particolare di quello di terzo, per cui uso comunque la quadratura a due punti.

Si osserva che, se l’integrale si estende tra valori generici a e b e non tra [-1,1], con opportuni cambi di variabile si può riportare l’intervallo di integrazione tra [-1,1], come richiesto dall’integrazione Gaussiana.

Infine l’integrale doppio può essere risolto tramite integrazione gaussiana poiché è definito come due integrali singoli concatenati. La soluzione è derivata dall’integrazione a due punti sull’intervallo monodimensionale: questo vuol dire che per l’integrale doppio basta campionare 4 punti con la regola di integrazione gaussiana.
Inoltre nell’integrale doppio tutti i pesi sono unitari, dato che la loro somma deve essere uguale a 4.

Per inizializzare una funzione del tipo f(x)=a0+a1*x su MAXIMA è possibile applicare vari metodi.

(n.b. con questa procedura rimane inalterato il carattere di espressione).

Oppure è possibile mantenerne il carattere di funzione:

-A. Strozzi, Progettazione Assistita di Strutture Meccaniche

-Minimal Maxima