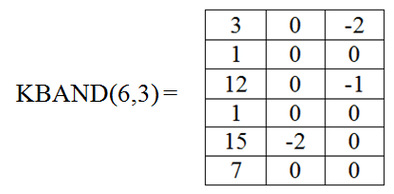Risultati Tubo in Pressione Mark/Mentat
Modello MSC.Marc verifica convergenza tubo prova_convergenza_v1.mud
Foglio di calcolo convergenza_errore_fem_v2.ods
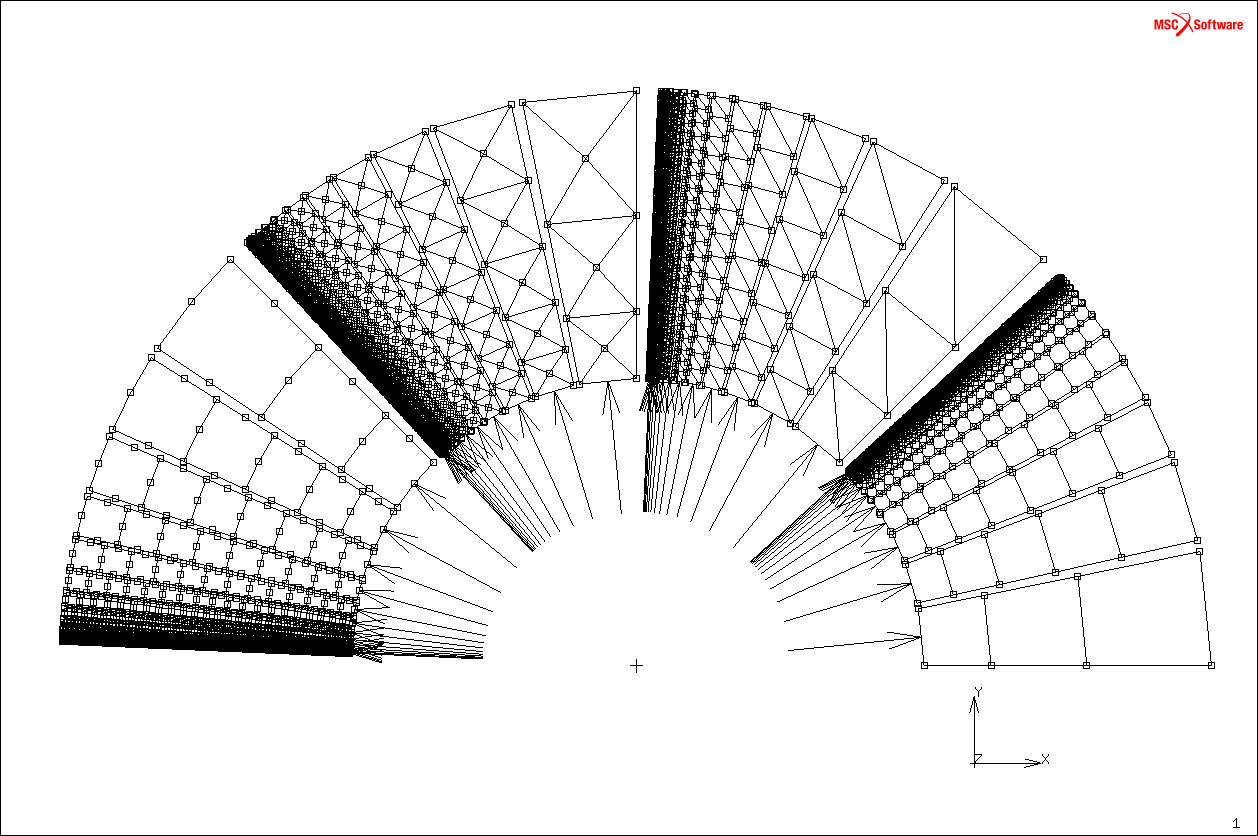
Nell'immagine riportata in alto è stata proposta una mappatura generale delle varie tipologie di mesh applicate al tubo in pressione al fine di poter fare un'analisi di convergenza e degli errori al variare del tipo di mesh e del suo infittimento. Le mesh risultano essere 4 rispettivamente [Isoparametrici 4 Nodi], [Isoparametrico 4 nodi suddiviso in Triangolari 3 nodi], [Isoparametrico 4 nodi suddiviso in Triangolari 3 nodi con nodo centrale], [Isoparametrico 8 nodi]. Abbiamo quindi per ogni mesh 13 livelli di raffinamento, in particolare tra un livello e l'altro c'è un fattore $\sqrt{2}$ e quindi ogni due livelli la dimensione degli elementi si dimezza.
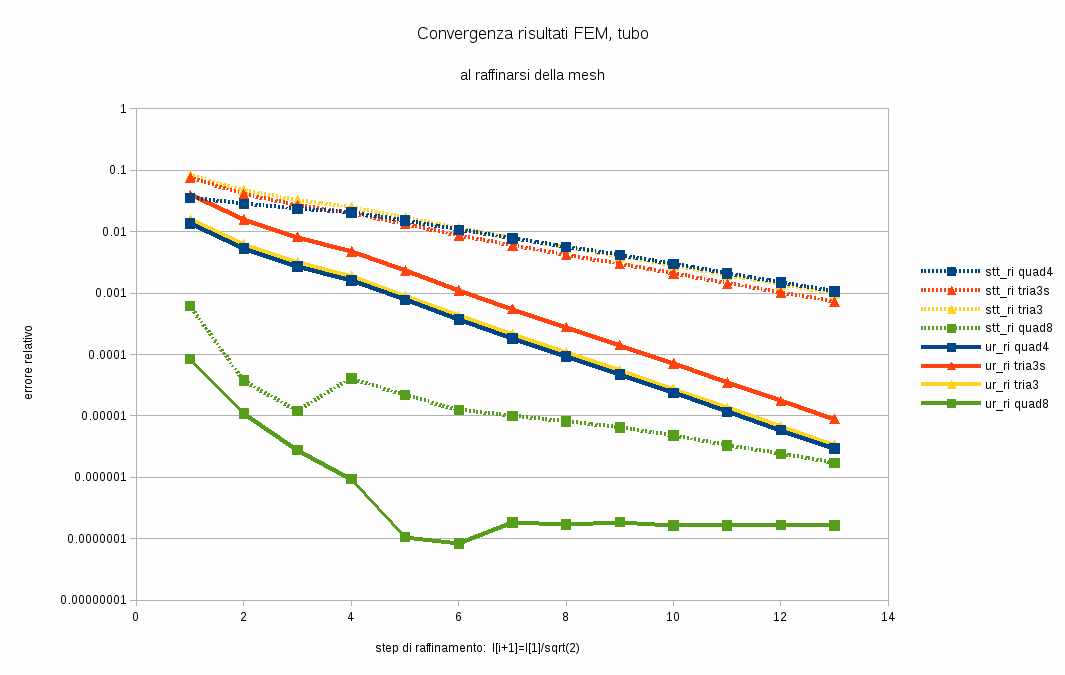
Nella seconda immagine sono stati campionati lo Spostamento Radiale(linee continue) del bordo interno del tubo e lo stato tensionale in termini di Tensione Circonferenziale(linee tratteggiate) per i 4 tipi di mesh al variare del raffinamento. Sull'asse delle ordinate sono riportati i valori degli errori su scala logaritmica (gli errori possono essere valutati rispetto ad un valore della soluzione esatta quando possibile oppure rispetto al valore della soluzione più precisa ottenuta). Come è possibile osservare all'aumentare dell'infittimento della mesh gli errori diventano sempre più piccoli secondo una legge abbastanza lineare (in un grafico bilogaritmico) per quanto riguarda i primi 3 tipi di mesh. Si osserva inoltre che l'Isoparametrico 8 nodi è troppo preciso: l'errore di spostamento radiale (tratteggio verde) minore è dell'ordine di $10^-7$ dopodichè non si riduce più, poichè l'errore di discretizzazione viene coperto dall'errore numerico; questo significa che infittire la mesh oltre una scala 6 non ha più utilità. Si può notare inoltre che globalmente gli errori di spostamento sono sempre minori rispetto a quelli delle tensioni, quindi nella FEM gli spostamenti sono più precisi.
Metodo di analisi dell'errore di un raccordo caricato a fatica
Consideriamo una struttura macroscopicamente grande con un raccordo piccolo. Questo raggio di raccordo crea problemi solo se caricato a fatica. Infatti se caricato staticamente, al massimo si può assistere ad un leggero snervamento del materiale, mentre se caricato a fatica potrebbero insorgere delle cricche. La regola empirica per fare un'analisi FEM di un raccordo di 90° è utilizzare una mesh di almeno 4 elementi per avere un errore ingegneristicamente accettabile. Se volessimo però condurre lo studio di un raccordo di 120° non abbiamo regole empiriche sulla mesh e quindi è necessario fare delle prove sull'errore al variare della mesh. Immaginiamo ora che la struttura sia assialsimmetrica e molto lunga; gli stati di caricamento (modi di frattura) possibili sono stati schematizzati in figura: TRAZIONE (Modo 1), TAGLIO ENTRO PIANO (Modo 2), TAGLIO FUORI PIANO (Modo 3). Quindi al variare dell'angolo del raccordo, tipo di mesh, infittimento della mesh e dello stato di caricamento è possibile eseguire diverse prove per verificare in quali casi si ottengono errori più bassi.
Punti di Singolarità in cui la FEM risulta inefficace
Immaginiamo di avere due blocchi soprapposti in maniera tale che si venga a creare uno spigolo vivo (convesso). Il blocco superiore viene caricato con una pressione distribuita sulla superficie superiore oppure semplicemente agisce la sua forza peso. Vogliamo quindi trovare la mesh ottimale per ottenere errore minimo in corrispondenza dello spigolo vivo e quindi calcolarne lo stato tensionale. Eseguendo varie prove con lo stesso tipo di mesh si scopre che all'aumentare dell'infittimento della mesh la tensione aumenta sempre. Quindi localmente i calcoli non giungono mai a convergenza o meglio convergono all'infinito. Infatti la teoria dell'elasticità ci dice che in questo tipo di condizioni lo stato tensionale nello spigolo è infinito. (Esempio: se consideriamo una lama di coltello infinitamente affilata lo stato tensionale che genererebbe su una struttura è infinito; infatti la forza che dovremmo applicare alla lama per tagliare qualsiasi materiale sarebbe 0) Per risolvere questo problema basterebbe ipotizzare di raccordare lo spigolo con un raggio di raccordo piccolissimo. Questo però renderebbe la costruzione della mesh molto più complessa. In questi casi quindi la FEM risulta inefficace a livello ingegneristico. Quando ci si presenta questo problema è sufficiente non curarsi dei risultati della FEM in prossimità dello spigolo vivo, poichè sappiamo dalla teoria dell'elesticità che quei risultati tensionali locali sono completamente sbagliati. N.B.: il resto della struttura comunque viene risolta in maniera corretta.
Altri due casi in cui la mesh risulta non utile sono:
1) L'incollaggio di due pezzi
2) Un carico concentrato su una superficie piana
In generale quindi si può dire che i punti di singolarità si hanno ogni qualvolta la struttura presenta degli angoli convessi e per individuarli è spesso utile ricorrere all'ANALOGIA FLUIDODINAMICA, che consiste nell'immaginare un fluido che scorre in prossimità di una superficie; gli angoli che virtualmente toccano il fluido sono convessi. Di conseguenza se si volesse fare un'analisi approfondita di questi punti di singolarità è necessario mettere da parte il calcolo computazionale, eseguire delle prove empiriche in laboratorio ed utilizzare dei misuratori di tensione. Questo metodo è sopratutto usato nel calcolo delle tensioni residue dei cordoni di saldatura (si usano gli estensimetri), poichè l'area del cordone sezione per sezione è quasi impossibile da modellare. Ovviamente esistono già delle normative che sono state ricavate da test sperimentali.
Matrice di rigidezza Bandata
Consideriamo la seguente matrice di rigidezza
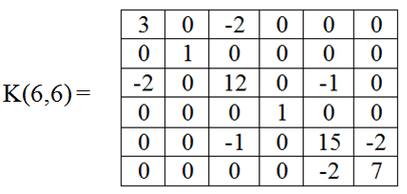 Analizzando la matrice di rigidezza piena della struttura, si può facilmente osservare che è simmetrica, ma molti elementi (più di metà) sono nulli e quindi la matrice risulta sparsa: un elemento è nullo se non esiste un ponte elastico che colleghi un certo gdl (indice di riga) di un nodo e un altro gdl (indice di colonna) di un altro nodo. Osservando il caso della figura, si può dire che, ad esempio, non essendoci un ponte elastico che leghi il nodo 1 al nodo 3, allora l'elemento alla riga 2 e colonna 5 è nullo.
Il costo computazionale aumenta all'aumentare degli elementi della matrice. Avere tanti elementi nulli significa dover stoccare più elementi inutilmente ed avere un costo computazionale maggiore, conviene quindi velocizzare il calcolo con lo stoccaggio dei soli termini non nulli.
Come si nota dalla matrice i termini non nulli si raggruppano lungo la diagonale principale della matrice. Posso, perciò, memorizzare i termini sopradiagonali (diagonale inclusa), inclusi in una banda di lunghezza tale da comprendere tutti i termini non nulli. La matrice che ricaviamo prende il nome di MATRICE BANDATA.
In particolare la diagonale principale della matrice piena diventa la prima colonna di quella bandata, la prima sopradiagonale della matrice iniziale diventa la seconda colonna della matrice bandata, la seconda sopradiagonale della matrice iniziale diventa la terza colonna della matrice bandata (facendo attenzione che gli ultimi due elementi sono nulli), e così via fino al completo riempimento della matrice bandata).La matrice bandata di questa matrice di rigidezza risulta quindi essere la seguente:
Analizzando la matrice di rigidezza piena della struttura, si può facilmente osservare che è simmetrica, ma molti elementi (più di metà) sono nulli e quindi la matrice risulta sparsa: un elemento è nullo se non esiste un ponte elastico che colleghi un certo gdl (indice di riga) di un nodo e un altro gdl (indice di colonna) di un altro nodo. Osservando il caso della figura, si può dire che, ad esempio, non essendoci un ponte elastico che leghi il nodo 1 al nodo 3, allora l'elemento alla riga 2 e colonna 5 è nullo.
Il costo computazionale aumenta all'aumentare degli elementi della matrice. Avere tanti elementi nulli significa dover stoccare più elementi inutilmente ed avere un costo computazionale maggiore, conviene quindi velocizzare il calcolo con lo stoccaggio dei soli termini non nulli.
Come si nota dalla matrice i termini non nulli si raggruppano lungo la diagonale principale della matrice. Posso, perciò, memorizzare i termini sopradiagonali (diagonale inclusa), inclusi in una banda di lunghezza tale da comprendere tutti i termini non nulli. La matrice che ricaviamo prende il nome di MATRICE BANDATA.
In particolare la diagonale principale della matrice piena diventa la prima colonna di quella bandata, la prima sopradiagonale della matrice iniziale diventa la seconda colonna della matrice bandata, la seconda sopradiagonale della matrice iniziale diventa la terza colonna della matrice bandata (facendo attenzione che gli ultimi due elementi sono nulli), e così via fino al completo riempimento della matrice bandata).La matrice bandata di questa matrice di rigidezza risulta quindi essere la seguente:
Per maggiore chiarezza si propone un esempio pratico di una trave incastrata.
Per ottenere una matrice bandata corretta è necessario che la numerazione dei nodi che costituiscono la mesh seguano un ordine ben preciso. Per descrivere questo ordine si propone l'esempio di una trave incastrata meshata. La numerazione seguirà il seguente ordine:
Se considero, ad esempio, il nodo 11 allora i nodi che contribuiscono a definirne l'equilibrio nella matrice di rigidezza sono 6,7,8,10,11,12,14,15,16. Quindi la numerazione va dal 6 al 16 e quindi tutti i nodi, in particolare tutti i gradi di libertà associati ai nodi numerati sotto il 6 e sopra il 16 non rientrano nell'equazione di equilibrio del nodo 11. In questo caso per come sono stoccati i gradi di libertà (a coppie di x,y) il nodo 6 è associato al g.d.l. 11,12 e il nodo 16 è associato al g.d.l. 31,32. Quindi se vogliamo considerare la traslazione lungo x del nodo 11, nella matrice di rigidezza andremo a leggere la riga 21 in cui troveremo che tutti gli elementi sotto l'elemento 11 e sopra l'elemento 32 sono nulli. Se quindi la numerazione viene fatta in questa maniera corretta accade che gli elementi non nulli vengono tutti condensati nell'intorno della diagonale della matrice. Questo facilita enormemente la creazione della Matrice Bandata, perchè si viene a generare una banda di stoccaggio. In più essendo la matrice simmetrica l'intorno superiore e inferiore rispetto la diagonale principale hanno elementi simmetrici e quindi è sufficiente memorizzare solo quella superiore riducendo della metà il costo computazionale della matrice bandata. Di seguito è riportato un esempio schematico degli elementi diagonali che vengono stoccati:
Per calcolare la larghezza di banda h di una matrice bandata è possibile utilizzare la seguente espressione:
$ h = n \left(I_{max} - I_{min} + 1\right)$
Dove:
1)Imax e Imin sono rispettivamente le numerazioni massima e minima del nodo considerato (nel nostro esempio erano 16 e 6);
2) n sono i gradi libertà nodali (nel nostro caso 2);
3) il +1 viene inserito per tener conto di elementi unitari (ovvero un nodo collegato con se stesso).
Quindi al massimo la larghezza di banda h sarà pari a n gradi di libertà (ovvero se Imax=Imin). Questo si verifica ad esempio quando consideriamo anelli chiusi:
In questo caso purtroppo anche se si utilizza la matrice bandata non si risparmia nulla a livello di costo computazionale.
Effetto computazionale della coincidenza di due nodi diversi della mesh
Può talvolta capitare di modellare un corpo che a riposo abbia elementi non congiunti, ma durante la deformazione due punti vengano a coincidere. Se capita un caso simile accade che il costo computazionale sale vertiginosamente e il calcolatore invece di terminare in 2 ore termina in 3 giorni. Questi casi possibilmente andrebbero evitati facendo in modo che il carico non sia tale da generare una deformazione che faccia coincidere alcuni nodi della mesh. Un esempio di tale caso è mostrato in figura:
Mappatura
Immaginiamo di avere una matrice di rigidezza qualsiasi piena o non piena. Ne abbiamo costruito correttamente la matrice bandata. Adesso voglio considerare un elemento qualsiasi entro banda della matrice di rigidezza e mapparla, ovvero trovare la sua posizione corrispondente nella matrice bandata. Consideriamo quindi l'elemento che abbia posizione nella matrice di rigidezza pari a (irow,icol).
Nella forma bandata l'elemento si troverà in:
$ ibandata_{row} = i_{row} $
$ ibandata_{col} = i_{col} - i_{row} + 1$