L'importanza di questo studio è improntata sulla potenzialità di riuscire ad applicare delle semplificazioni e conseguentemente una riduzione delle risorse di calcolo necessarie alla risoluzione di sistemi complessi. Un corpo si dice in tensione piana quando gli elementi

$\sigma_z=\tau_{xz}=\tau_{yz}=0$

Tralasciando la definizione matematica si vuole cercare un significato fisico a questo particolare stato tensionale.

Condizione necessaria affinché un corpo si trovi in stato tensionale piano è che presenti un piccolo spessore rispetto alle altre dimensioni, un corpo con queste caratteristiche è detto lastra quando è caricato lungo il suo piano. Uno stesso corpo può essere definito infatti come lastra o come piastra la differenza risiederebbe solo nel modo in cui esso è caricato;

• LASTRA : Corpo di piccolo spessore (lungo z) caricato sul piano xy a trazione/compressione
• PIASTRA: Corpo di piccolo spessore (lungo z) caricato sul piano xz a flessione

Nel primo caso si ha una lastra che rispetta le condizioni di tensione piana essendo caricata solo lungo l'asse y, sulle facce laterali è presente solo la pressione atmosferica che essendo presa come riferimento si considera nulla. Quindi essendo la lastra molto sottile si può considerare che pure al suo interno la $\sigma_z$ rimanga praticamente nulla.

Si noti dalla figura come la presenza di un foro (fig. b) o di spigoli (fig. c) possano dar luogo a dei gradienti significativi che influenzano anche le componenti $\sigma_z$ che nella (fig. a) erano nulli.

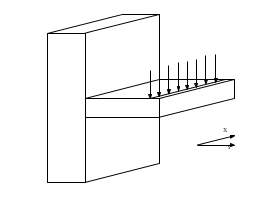
Un altro caso di particolare interesse, è quello mostrato in (fig. d) in cui la lastra è rigidamente connessa ad un basamento, si può immaginare come fosse saldata, in queste condizioni il carico trattivo applicato alla lastra tenderebbe a far diminuire la sezione della faccia attaccata al basamento per Effetto Poisson. Nella circostanza in cui ci sia un vincolamento rigido della lastra al basamento il restringimento della sezione non può avvenire; ciò porta a concludere che si innescano delle tensioni $\sigma_z$ che si oppongono alla contrazione della sezione lasciandola in configurazione indeformata. Quindi in prossimità del basamento la lastra non si trova in condizioni di tensione piana.

Supponiamo di avere un cilindro in gomma posto tra due piani infinitamente rigidi (fig. a). Le condizioni di deformazione piana possono essere espresse in termini matematici imponendo nulle le deformazioni con componente z;

$\epsilon_z=\gamma_{xz}=\gamma_{yz}=0$

Come nel caso di tensione piana la condizione necessaria prevedeva uno spessore molto piccolo, in condizioni di deformazione piana il corpo deve essere molto lungo; inoltre deve essere caricato solo sul piano xy e le sezioni perpendicolari all'asse z devono essere tutte simili tra loro ed ugualmente caricate.

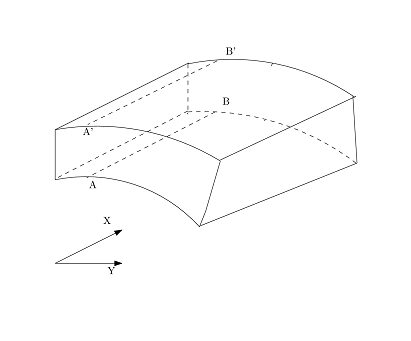
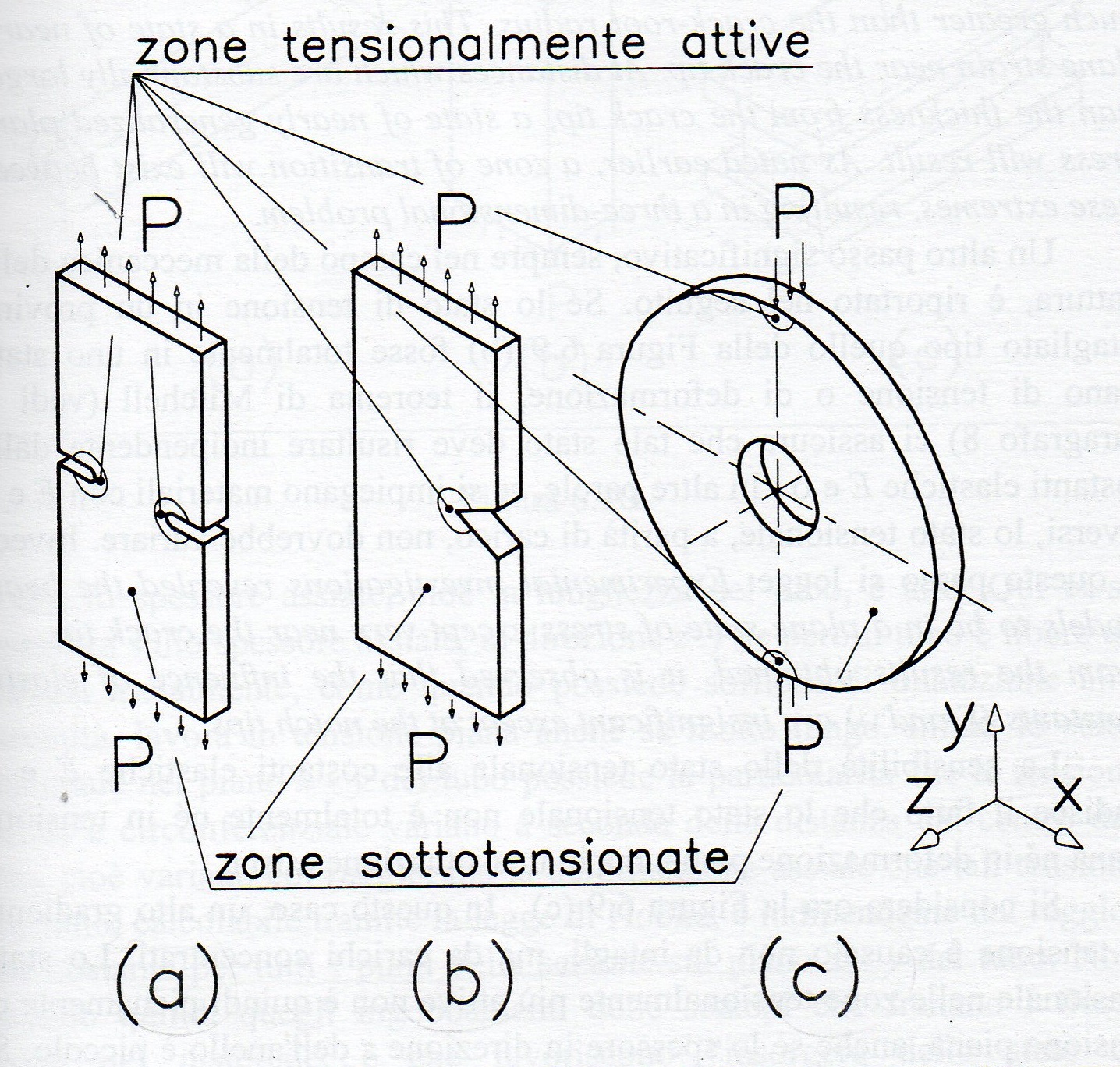
Riprendendo il caso in (fig. a) supponiamo che non ci sia attrito tra il cilindro e i piani, saremo inizialmente in configurazione indeformata (fig. b e c), appena viene applicata una forza esterna P il cilindro subisce una leggera deformazione, supposto che il carico rientri nel campo elastico, tale deformazione da origine ad un contatto di tipo Hertziano. La zona di contatto è molto piccola rispetto alle dimensioni del diametro, in una vista frontale è possibile distinguere due zone rispettivamente una sotto caricata ed una zona tensionalmente attiva che possono essere viste come il cuore della sezione circolare ed una sorta di boundary layer. Per zona sottocaricata si intende una zona in cui le deformazioni sono estremamente piccole ragione per cui può essere considerata come rigida, la zona tensionalmente attiva interessa solo i primi strati di materiali adiacenti alla zona di contatto. Effettuando uno zoom sulla sezione frontale (fig. f) è possibile mettere in risalto un flusso laterale di materiale che non interessa ai fini dello studio della deformazione piana, particolare importanza ricopre invece il flusso assiale essendo un effetto diretto della deformazione lungo z $\epsilon_z$. Considerando solo metà cilindro e immaginando di suddividere la sezione trasversale in tanti piccoli rettangoli, si avrà che ogni rettangolo subirà un allungamento lungo z che si sommerà nelle varie sezioni successive (fig. g). In base a questa valutazione puramente fisica, si capisce come per un cilindro infinitamente lungo verrà a crearsi un baffo molto lungo. Ma a rigor di logica ci aspettiamo che nella realtà il baffo abbia dimensioni molto contenute. Allora giungiamo alla conclusione che le zone con comportamento rigido tendono a bloccare il flusso assiale per gran parte del corpo, per quanto detto allora possono essere considerate in deformazione piana, e le uniche sezioni che presentano un flusso assiale sono quelle più vicine alle estremità (fig. i).

Vediamo il seguente altro esempio di Deformazione piana

Nello schema sopra riportato sono presenti due rulli molto lunghi formati da materiale metallico ricoperti da uno strato elastomerico che supponiamo di schiacciare.

La parte centrale è in metallo di conseguenza possiamo considerarla infinitamente più rigida della gomma e pertanto indeformabile; la gomma, di conseguenza, non può fluire assialmente perché è trattenuta dalla parte centrale ovvero dal metallo stesso. Quindi è possibile considerare il sistema in deformazione piana $\epsilon_z$=0

In realtà il materiale non è completamente in deformazioni piana perché essendo le facce estremali a contatto con aria, esse hanno una $\sigma_z$=0 pertanto in tensione piana; quindi avremo una piccola porzione di materiale vicino alle facce che si troverà in una zona di transizione di cui non ne conosciamo esattamente l'estensione ma sappiamo essere né in tensione piana né in deformazione piana. Possiamo però concludere che essendo il materiale molto lungo, esso sarà per la quasi totalità della sua lunghezza in deformazione piana quindi in tal caso si dice che la deformazione piana prevale sulla tensione piana.

Nucleo del dente di una ruota dentata

sorgente ipe

Finora abbiamo analizzato casi Hertziani, ora invece studieremo un caso in cui non valgono le ipotesi del contatto Hertziano. Questo modello didattico rappresenta il nucleo del dente di una ruota dentata. Ha un punto di grande complessità, ha due effetti che contrastano.

sorgente ipe

Caricando il nostro dente notiamo che le fibre tese si trovano nella parte superiore mentre le fibre compresse si trovano nella parte inferiore. La parte complessa dello studio della deformazione di questo modello sta nel fatto che si generano delle tensioni secondarie dovute all'effetto Poisson. Il mio modello non è in deformazione piana poichè noto che dove sono presenti le fibre tese ho un accorciamento del dente in direzione x , dove invece sono presenti le fibre compresse noto un allungamento del modello in direzione x. Se il dente è abbastanza lungo ho un cilindro centrale e due baffi laterali che vanno verso l'alto. Infatti ho una zona centrale in stato di deformazione piana(circa il 95%) mentre le zone laterali sono in stato di tensione piana.

Guarnizione elastomerica

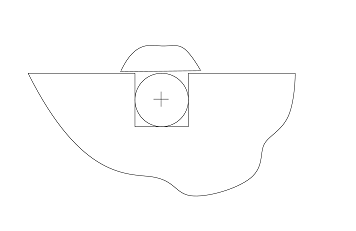
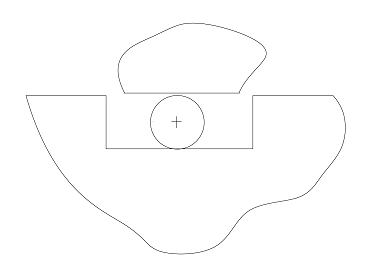
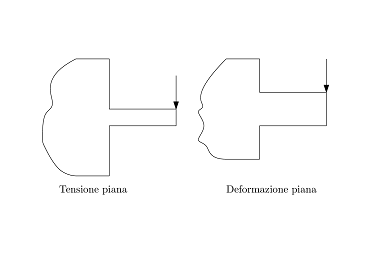
Un altro campo d'interesse è quello delle guarnizioni elastomeriche. Nelle figure sono rappresentati due montaggi differenti: *GIOCO NULLO : cava di sigillo tangente alla guarnizione *GIOCO NON NULLO: cava di sigillo più larga

sorgente ipe

Nel primo caso la guarnizione è vincolata lateralmente e non può deformarsi lungo la direzone z, nascono così delle tensioni lungo la suddetta direzione. Questo è uno stato di deformazione piana. Con questo montaggio riesco ad avere delle reazioni più alte da parte della guarnizione.

sorgente ipe

Nell'altro caso ho una deformazione lungo la direzione z tuttavia e tensioni lungo questa direzione non ci sono o sono trascurabili. Questo infatti è uno sato di tensione piana. Per studiare le guarnizioni non esamino i carichi ma studio princiamente le deformazioni. A parità di schiacciamento nei due montaggi (ad esempio il 20%) ho una pressione più alta nel primo montaggio, dunque raggiungo pressioni di contatto più elevate. Nella figura qui sotto sono rappresentati due oggetti, il primo in tensione piana ed il secondo in deformazione piana. Per averlo in deformazione piane devo avere uno spessore maggiore. Noto che il caso in tensione piana ha una freccia maggiore rispetto al modello in deformazione piana. Se ho meno vincoli aumenta la deformazione.

sorgente ipe

Cabina dell'ascensore

sorgente ipe

Un altro esempio è quello della cabina del'ascensore. Ho un carico P con direzione verticale. La traversa è sostenuta da due tiranti A e B uguali tra loro salvo per la lunghezza. Inoltre grazie ai carrelli la traversa non può ruotare. Quando agisce il carico P verso il basso esso non verrà ripartito in maniera equa ma il tirante che si deformerà di meno prenderà la parte maggiore del carico, in questo caso sarà il tirante B. Le zone laterali di un dente dal momento che risultano essere in tensione piana, quindi maggiormente deformabili, prendono meno carico.

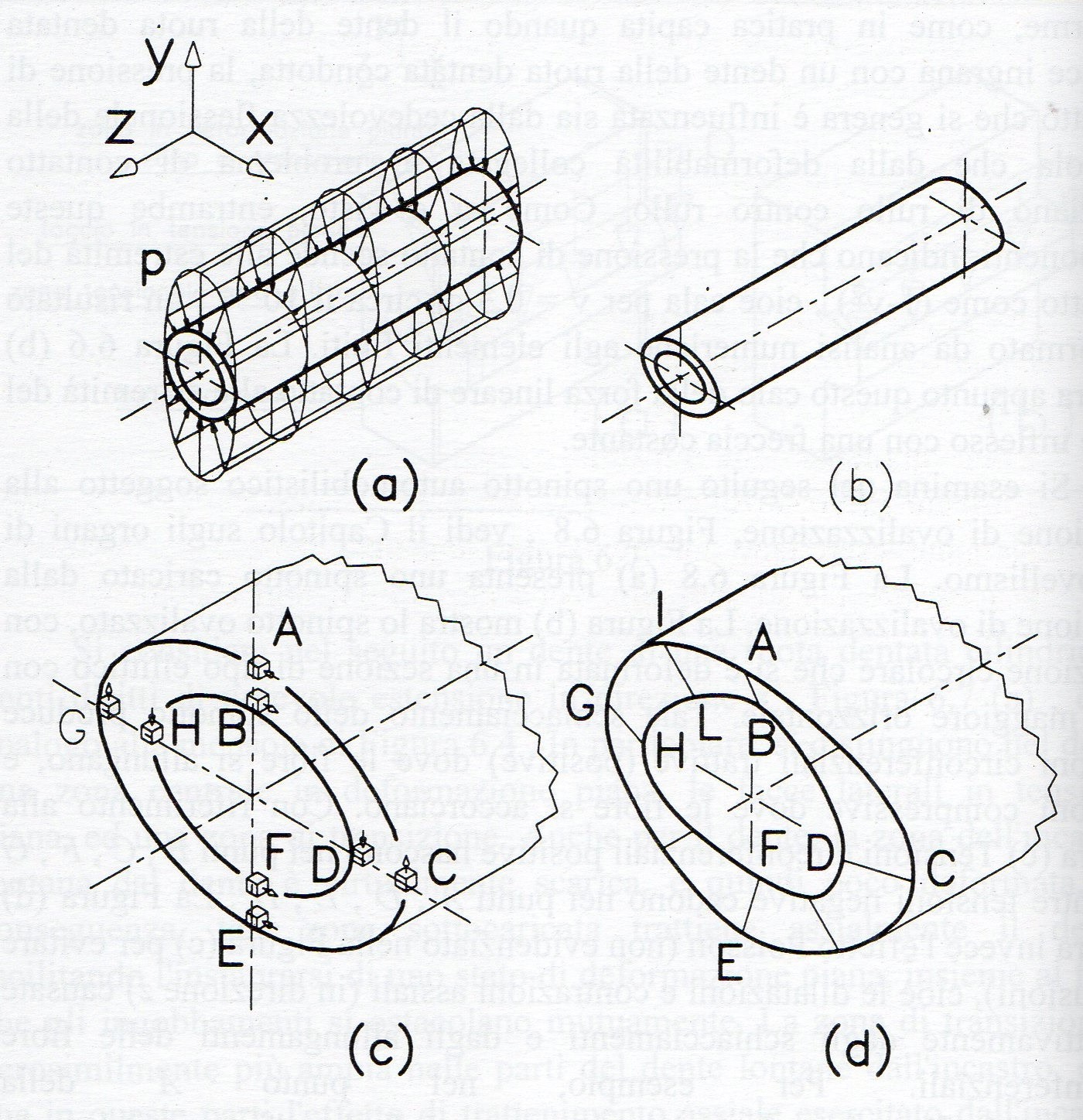
Un caso più complicato è lo spinotto automobilistico soggetto a carico flessione e di ovalizzazione. Lo spinotto è schiacciato assialmente dalle portate del pistone e lateralmente dal supporto della biella. In (b) lo spinotto si schiaccia, la parte superiore dell'elemento è compressa e la parte inferiore è tirata. La deformata risulta quasi piatta. Per l'effetto Poisson, se in (a) comprimo un cilindro di gomma, le fibre assiali si allungano. Quindi in A, D, E, H lo spinotto si allunga assialmente, mentre in B, C, F, G si accorciano. Ci sono quattro zone di transizione che che non si allungano e non si accorciano. Ne segue che le varie sezioni dello spinotto, tranne la sezione in mezzeria, tendono ad ingobbarsi, ma questi ingobbamenti, diventando sempre maggiori allontanandosi dalla mezzeria dello spinotto, si ostacolano a vicenda, favorendo l'instaurarsi della deformazione piana nello spinotto.

Controesempi

Generalmente le zone in cui i gradienti di tensione sono enormi, sono vicine a zone sottocaricate o sottotensionate considerate rigide. Il tondino in figura avrebbe la tendenza a restringersi, ma in realtà è contornato da materiale scarico che lo trattiene ed è un caso a metà fra la tensione e la deformazione piana.

Caso ©: a differenza dei casi a e b sopra riportati in cui le lastre non sono in tensione piana a causa di gradienti indotti da intagli, ora il disco è schiacciato con una forza concentrata linearmente, che provoca comunque gradienti elevati. Il segmento schiacciato tenderebbe ad allargarsi, ma è vicino a zone sotto caricate che impediscono la deformazione. Quindi per i casi di tensione piana, non è sufficiente specificare che la lastra è in parete sottile, ma bisogna specificare che non ha grandi gradienti tensionali, altrimenti avrei zone che tendono ad ostacolarsi.

In egual modo, esistono corpi infinitamente lunghi che non sono in deformazione piana. caso ©: un quadrato di gomma schiacciato fra due piani rigidi senza attrito. Nel momento in cui il corpo è compresso, tende ad allungarsi all'infinito, ma essendo composto da tante sezioni uguali, pur essendo un corpo lungo è in TENSIONE PIANA.

caso (a): Tubo soggetto a pressione interna libero di dilatarsi assialmente come nel caso in cui avesse i soffietti. Il tubo tende ad allungarsi e quindi a deformasi assialemente, ma le facce e stremali restano piane. Quindi un tubo, anche molto lungo, può essere come in questo caso in TENSIONE PIANA.

caso b: trave in grosso spessore sia in direzione x sia in direzione z. Si genera nel corpo uno stato tensionale uniforme monodimensione in direzione y e quindi non avvengono ingobbamenti delle sezioni. Il corpo risulta in tensione piana sia in direzione x sia in direzione z. Siccome i piani perpendicolari alla direzione z traslano senza ingobbarsi, per tutti i punti del corpo si ha epsilonz=cost, situazione chiamata deformazione piana generalizzata.

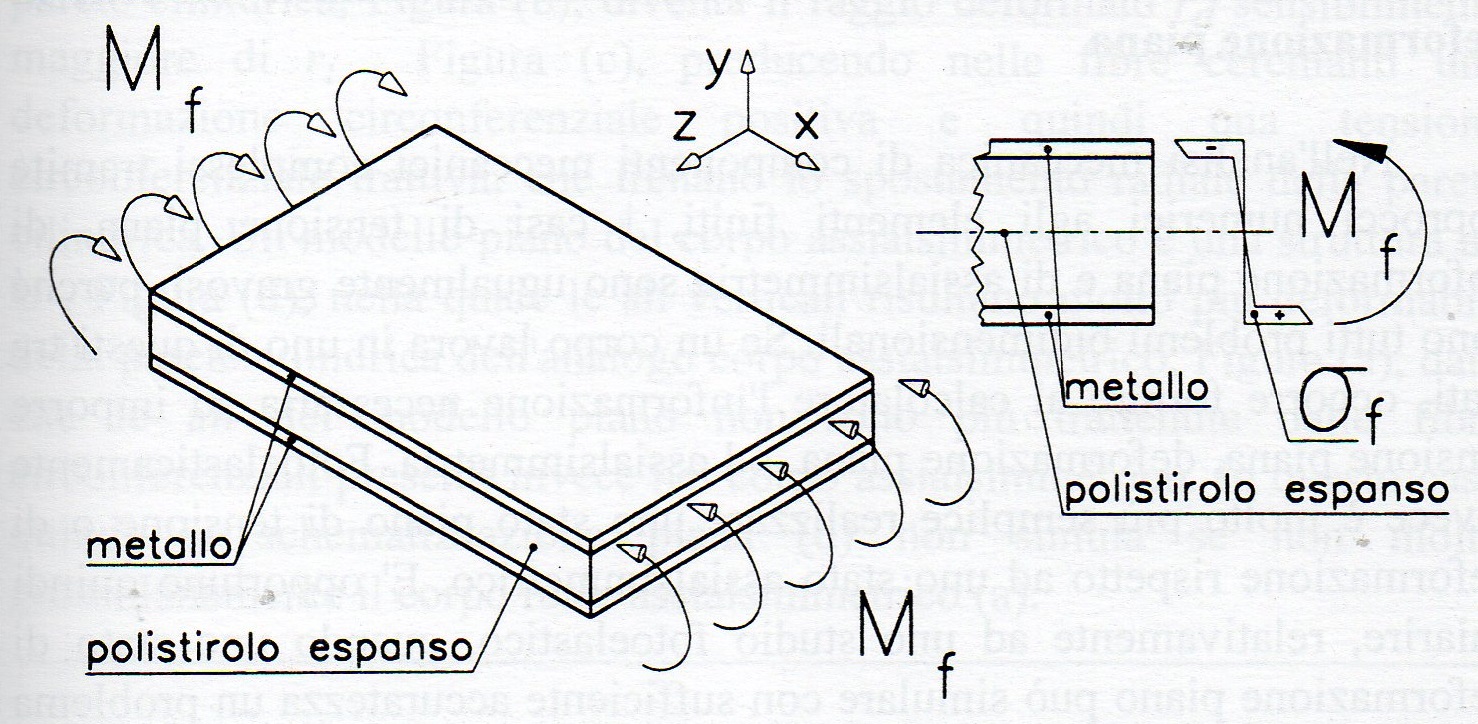
Caso di due lastre metalliche con distanziale isolante di polistirolo espanso soggetto a flessione. Le tensioni nell'anima di polistirolo sono molto minori delle tensioni nella lamine metalliche, dato che queste ultime sono più rigide e assorbono una aliquota maggiore di carico. Perciò il polistirolo non è in grado di precludere le contrazioni in direzione z delle due lamine metalliche, quindi queste ultime lavorano in condizione di tensione piana. Un esempio del genere è associabile al caso della mensola o al dente della ruota dentata. Una modellazione di questo tipo non è in deformazione piana.

Il teorema di Michell permette di capire in quali casi piani le tensioni sono indipendenti da E e $\nu$

a) Corpo senza fori:

Le uniche condizioni al contorno presenti sono sulle $\sigma$ perciò non avendo fori ne condizioni al contorno sugli spostamenti ricade perfettamente nel teorema di Michell cioè le tensioni sono indipendenti da E e $\nu$. Ciò vuole dire che se dovessi studiare il caso con la FEM ed imporre E=10 Mpa oppure E=10000 Mpa il risultato ottenuto sarebbe lo stesso.

b) Corpo con foro autoequilibrato:

Condizioni al contorno sulle tensioni ma non sigli spostamenti. Pur avendo fori ma con carico autoequilibrato vale il teorema di Michell. Infatti possiamo prendere come esempio i tubi pressurizzati, nelle cui formule delle tensioni non compaiono E e $\nu$.

c) Albero-mozzo:

Condizioni al contorno sugli spostamenti perché ho un accoppiamento con interferenza cioè albero compresso e mozzo in trazione. Perciò il teorema di Michell NON vale in questo caso dato che ho condizioni sugli spostamenti.

d) Dente di ingranaggio incastrato:

In questo caso parte delle condizioni al contorno sono sugli spostamenti perciò Michell NON vale. In realtà se volessi calcolare le tensioni nella zona raccordata usando Michell, questo sarà comunque in grado di darmi risultati molto buoni e simili alla realtà perché sono lontano dalla zona vincolata dove sono state imposte le condizioni sugli spostamenti.

e) Piede di biella:

Carico non autoequilibrato con foro. Michele NON vale. Ciò vuol dire che se dovessi cambiare E oppure $\nu$ cambierebbero le $\sigma\

f) Mola rotante:

Michell NON vale per carichi inerziali come in questo caso.

g) Contatto brugola-maschio/femmina:

Condizioni al contorno solo sulle tensioni e non sugli spostamenti. Possiamo notare la presenza di una pressione triangolare su ogni lato che si estingue a metà lato. Il foro non è autoequilibrato però in base al teorema di Michell se la risultante del foro è una coppia pura, allora il teorema vale; perciò in questo caso è confermata la validità del teorema di Michell.

Concludendo possiamo affermare che il teorema di Michell è applicabile se la struttura non ha fori, oppure se li ha, il carico deve essere bilanciato o deve essere una coppia pura; inoltre le condizioni al contorno devono essere sulle tensioni e non sugli spostamenti. In questi casi il calcolo delle tensioni e indipendente dai valori assunti da E e $\nu$.