Indice
Equazione integrale nei problemi di contatto
•Semipiano elastico con un carico concentrato $P$
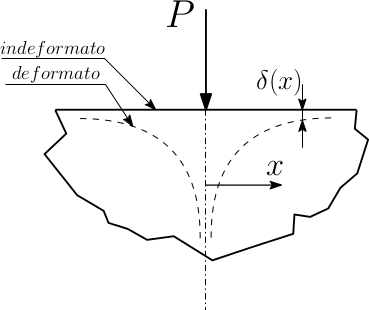
Si parte dal problema di un semipiano elastico con un carico concentrato $P$. Poiché il carico è concentrato, l'abbassamento del bordo superiore del semipiano va come in figura (matematicamente va a $-∞$).
Se si prende l'asse $x$ a partire dalla forza $P$, l'abbassamento $\delta(x)$ sarà dato da:
$\delta(x)=\frac{P}{E}log|x|$
Questa soluzione è chiamata soluzione di Boussinesq. E' formalmente esatta, però presenta degli aspetti criticabili: mentre è accettabile che $\delta(0) = ∞$, non va bene che $\delta(∞) = ∞$, cioè non va bene che $\delta(x)$ sia infinito quando ci si trova lontano del carico $P$.
•Semipiano elastico con due carichi concentrati $P_{1}$ e $P_{2}$
Quando abbiamo un solo carico è naturale prendere l'asse $x$ a partire dal carico e definire $\delta$ come $\delta(x)$. Il problema sorge quando ho più di un carico.
Se si hanno due carichi $P_{1}$ e $P_{2}$, non mi basta più una variabile $x$ per definire l'abbassamento, ma me ne servono due: la variabile $x$ definirà la posizione dei carichi $P_{1}$ e $P_{2}$ rispetto ad un punto arbitrario, mentre la variabile $y$ indicherà la posizione in cui calcolare l'abbassamento.
Non va bene usare solo $x$ altrimenti troverei sempre lo spostamento sotto il carico in questione, mentre lo spostamento lo si vuole in un punto qualunque.
$\delta(y)=\frac{P_{1}}{E}log|x_{1}-y| + \frac{P_{2}}{E}log|x_{2}-y|$
•Semipiano elastico con un carico distribuito $p(x)$
L'esempio con la pressione distribuita è una generalizzazione dei carichi concentrati, infatti si può dire che la pressione di contatto è costituita da infinite forze infinitesime $dP = p(x)dx$ adiacenti.
La relazione tra abbassamento e carico distribuito ha una forma del genere:
$\delta(y)=\frac{1}{E}\int_{x_1}^{x_2} \underbrace{p(x)\, dx}_{forza\ infinitesima} \log|x-y|$ , $ \quad $ anche se in realtà il $dx$ andrebbe alla fine: $ \quad $ $\delta(y)=\frac{1}{E}\int_{x_1}^{x_2}\,p(x)\,log|x-y|\,dx$ $ \quad $ $(*)$
Tale equazione presenta:
• una variabile esterna $y$
• una variabile interna $x$
Se sapessi risolvere l'integrale (per esempio, se $p(x) = cost$ lo so risolvere), $x$ va via e rimarrebbe solo $y$, quindi $x$ è la variabile d'integrazione detta variabile interna o dummy variable.
L'equazione integrale $(*)$ può essere vista in due modi distinti:
1) si conosce $p(x)$, per esempio se $p(x) = cost$ $ \ $ l'integrale del logaritmo lo si conosce e si può ricavare $\delta(y)$;
2) $p(x)$ è un'incognita e si conosce $\delta(y)$ $\longrightarrow$ questa è la vera problematica interessante dell'equazioni integrali!
•Indentatore rigido rettangolare a spigoli vivi
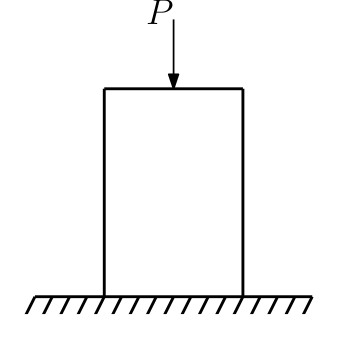
Il più semplice esempio di equazione integrale è quella relativa all'indentatore rigido. Si ha un indentatore rigido a spigoli vivi che viene schiacciato contro un semipiano elastico.
Questo problema può essere trattato con l'equazione integrale: infatti nel tratto a contatto col semipiano il $\delta(y)$ rimane costante poiché l'indentatore si abbassa senza ruotare e rimane quindi da trovare l'espressione di $p(x)$. L'equazione integrale per questo problema è stata risolta.
Per ragioni matematiche non conviene riferirsi all'equazione nella forma $(*)$, ma conviene derivarla rispetto alla variabile esterna:
$\frac{d\delta(y)}{dy}=\frac{1}{E}\int_{x_1}^{x_2}\,\frac{p(x)}{y-x}\,dx$ $\longrightarrow$ questa è la forma standard dell'equazione integrale dei problemi di contatto.
Gli integrali del tipo $\int_{x_1}^{x_2}\,\frac{p(x)}{y-x}\,dx$ sono detti integrali di Chebyshev o di Chauchy. Per capire le problematiche di quest'integrale supponiamo $p(x) = cost$ e guardiamo la figura sottostante:
Si nota che quando $x$ è prossima a $y$ il denominatore va a zero e la funzione va a $+∞$ o a $-∞$. Siccome il denominatore passa per zero, la funzione nel suo complesso ha una discontinuità saltando da $+∞$ a $-∞$. Si riesce a dimostrare in molti casi che le due punte che vanno a $∞$ si compensano e l'integrale non è più divergente.
Nel caso di indentatore rigido con superficie piana che schiaccia un semipiano elastico, la quantità $\frac{d\delta(y)}{dy}=0$ (perché $\delta(y)=cost$), quindi rimane da risolver l'integrale.
Tale integrale si riesce a risolvere e la pressione di contatto avrà il seguente andamento:
In corrispondenza degli spigoli vivi, $p(x)$ va a $∞$ come $\frac{1}{x}$.
La soluzione di questo caso particolare è presa come soluzione di riferimento.
•Indentatore rigido rettangolare con spigoli arrotondati
La soluzione interessante però è quella di indentatore rigido con spigoli arrotondati su semipiano elastico (se l'indentatore fosse anch'esso elastico non si arriva alla soluzione).
Questa soluzione ci dà l'effetto intaglio in funzione del raggio di raccordo.
Si noti che questo è un contatto progressivo, cioè più si schiaccia più l'area di contatto aumenta, ma l'aumento dell'area di contatto aumenta poco (solo del 2÷3%), quindi il problema è quasi lineare.
Non c'è una formula di validità generale che ci dice quanto vale esattamente la pressione in corrispondenza di uno spigolo arrotondato: sappiamo che è finita, ma per stimarla si fa un'analisi FEM.
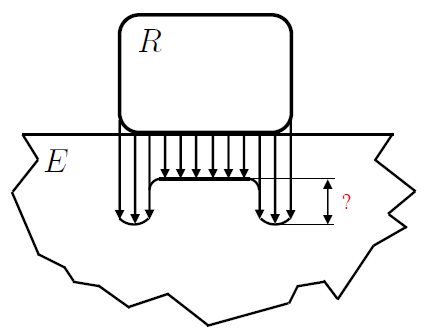
Si osservi che se l'indentatore rigido diventa sempre più largo avremo che:
• in prossimità dei raggi di raccordo la pressione va in su (effetto hertziano);
• al centro mi aspetterei che la pressione si appiattisca e arrivi ad un valore costante, ma la matematica mi dice che la pressione tende a zero.
Quest'ultima osservazione è spiegabile matematicamente in questo modo: la soluzione di un'equazione integrale ha la particolarità di essere essa stessa integrabile, però si è notato che se la pressione di contatto su una zona di lunghezza $∞$ non è zero allora il suo integrale è $∞$.
In sostanza l'unica conoscenza del ruolo del raggio di raccordo sull'effetto intaglio viene dall'equazione integrale, poi si effettua un'analisi FEM per confrontare i risultati.
Uno spigolo arrotondato si sposa con dolcezza col semipiano elastico, come mostrato in figura:
La pressione di contatto tra indentatore con spigoli arrotondati e semipiano elastico ha un andamento a schiena di cammello. E sapere quanto la pressione di picco sia più alta di quella centrale è un $\alpha_{k}$, quindi c'è un interesse tecnico.
Esempi di contatti con spigoli arrotondati sono i seguenti:
• il contatto tra la testina delle protesi d'anca e la cavità femorale in cui viene infilata;
• contatti con guarnizioni elastomeriche rettangolari a spigoli arrotondati (ingegneria aeronautica).
Nella realtà però l'interesse più forte viene dal forzamento albero-mozzo (caso assialsimmetrico): si noti che la formula di Boussinesq è piana e non ne esiste una analoga per l'assialsimmetria.
Non ancora si riesce a capire dove si spacca il mozzo:
• se appena fuori la zona di contatto: se si spacca fuori, la causa è che l'albero è schiacciato dal mozzo, diventa conico come deformata, la deformata fa crescere delle $\sigma_{assiali}$ positive che dovrebbero essere la causa del crac;
• se appena dentro la zona di contatto: se si spacca dentro possiamo interpretarlo come fretting fatigue (dovuta allo sfregamento delle due superfici interessate).
I portali
•Portale caricato da una forza concentrata verticale
Si vuole calcolare l'andamento del momento flettente $M_{f}$ in tale struttura: questa è una struttura ad anello chiuso, in se iperstatica, e non è facile andare a determinare a prima vista le reazioni vincolari.
Per aver un'idea di come sia l'$M_{f}$ si cerca di intuire la deformata della struttura (procedimento più facile del calcolo delle reazioni). Poi naturalmente so che l'$M_{f}$ è lineare a tratti e so che va disegnato dalla parte delle fibre tese.
Ci sono due regole per capire la deformata del portale:
1) la conservazione dell'angolo retto
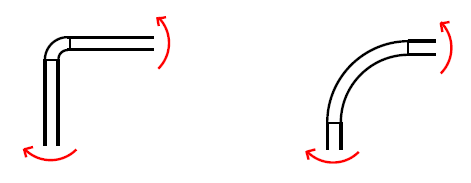
Guardo la deformata nell'intorno dello spigolo:
• se la zona curva è molto corta, cioè non c'è un raggio di raccordo ampio, si deformerà poco e potrò dire che vale appunto la conservazione dell'angolo retto (si parla di angolo retto perché angoli diversi dal retto sono poco comuni): l'asse curvo compreso tra le due sezioni che definiscono le zone rettilinee è così corto che le sezioni non potranno ruotare l'una rispetto all'altra;
• se la zona curva è lunga, cioè presenta raggio di raccordo ampio, ci sarà qualche rotazione tra le due sezioni.
2) la conservazione della curvatura
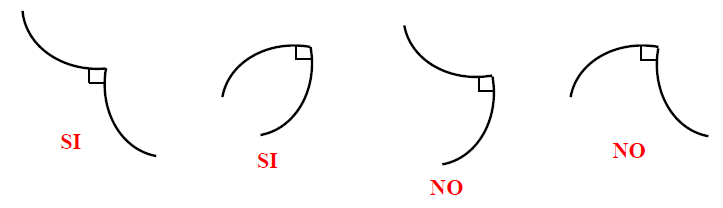
Il momento flettente in una zona di trave non caricata è lineare, inoltre se si prendono due punti vicini $A$ e $B$ è facile che in tali punti l'$M_{f}$ abbia lo stesso segno (questo non è un teorema, ma è improbabile che in due punti vicini l'$M_{f}$ cambi di segno). Da questa considerazione segue il seguente schema riguardante le curvature:
Il NO vuol dire “assolutamente improbabile” ed in questi due casi l'$M_{f}$ si è annullato sullo spigolo (c'è infatti un cambio di curvatura).
Ora vado alla ricerca dell'$M_{f}$ operando una soluzione per gradi.
Indebolisco il telaio inserendo due cerniere. La deformata della traversa sarà quella in verde perché le colonne si comporteranno come due appoggi.
Tolgo le cerniere e ripristino la continuità della struttura. Poi applico la prima regola, cioè la conservazione dell'angolo retto.
Si noti però che non c'è la conservazione della curvatura, quindi la deformata non va bene.
Per ricondurmi ad uno dei due casi corretti (quelli indicati col SI), vado a vedere quanti flessi possono esserci sulle traverse e nelle colonne. Si noti innanzitutto che un punto di flesso si ha dove l'$M_{f}$ taglia l'asse della struttura, cioè dove $M_{f}=0$. Si noti inoltre che stiamo studiando un caso simmetrico.
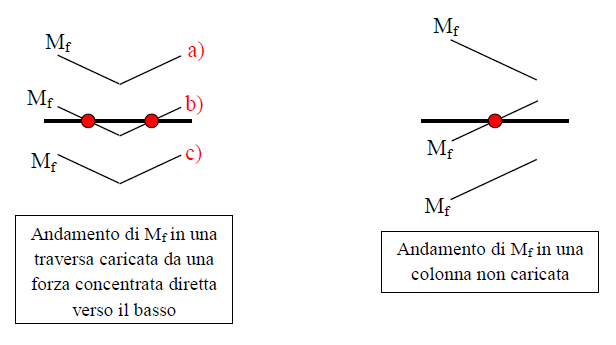
• traversa (tratto caricato): in $a)$ e $c)$ non c'è nessun flesso, in $b)$ ci sono due flessi, quindi nella traversa ci sono o 0 flessi o 2 flessi.
• colonne: sono zone non cariche e l'andamento di $M_{f}$ è rettilineo, cioè lineare (e non bilineare come nella traversa), essendo il tratto di trave in questione non caricato da forze esterne. Quindi le colonne hanno 0 flessi o 1 flesso.
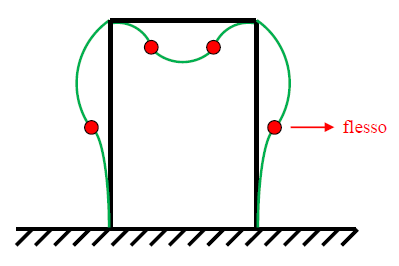
Le colonne hanno già un flesso, quindi affinché abbia la conservazione della curvatura dovrò aggiungere due flessi sulla traversa. La deformata qualitativamente corretta è la seguente:
Per tracciare il diagramma dell'$M_{f}$ ritorno sull'indeformata e individuo qualitativamente i flessi. Poi traccio $M_{f}$ dalla parte delle fibre tese:
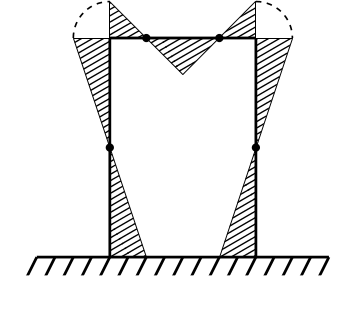
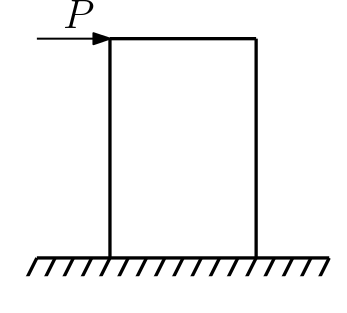
•Portale caricato da una forza concentrata orizzontale
In questo secondo esempio abbiamo una struttura geometricamente simmetrica (e con vincoli simmetrici) caricata in modo antisimmetrico: mi aspetto una deformata antisimmetrica.
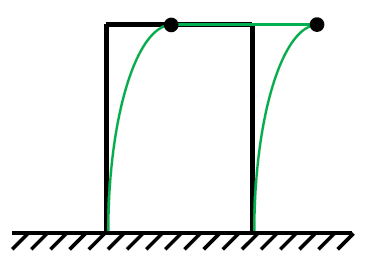
Aggiungo due cerniere per indebolire la struttura e questa è la prima deformata (lavorano le colonne e non la traversa, che rimane rettilinea perché non prende $M_{f}$):
Questa prima deformata non conserva l'angolo retto, quindi eliminiamo le cerniere e applichiamo la regola della conservazione dell'angolo retto:
Qui però non c'è conservazione della curvatura, quindi si dovrà cambiare la curvatura della deformata in zone abbastanza vicine ai punti di spigolo aggiungendo dei flessi.
• La traversa non ha carichi, essendo il carico presente un carico d'estremità (dal punto di vista matematico dovremo parlare, invece che di “traversa”, dell'aperto della traversa). Quindi nell'aperto della traversa l'$M_{f}$ è lineare e quindi la traversa o ha 0 flessi o 1 flesso.
• Stesso discorso per le colonne perché anche qui il caricamento è su un punto estremale (se parlo di “aperto” il punto estremale va fuori).
Noto che nella traversa c'è già un punto di flesso, quindi non può averne altri: si noti infatti che se aggiungessi un altro punto di flesso sulla traversa, in realtà ne dovrei aggiungere due in modo da avere un numero dispari di flessi, essendo il caricamento antisimmetrico.
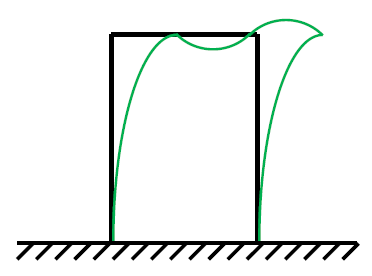
Di conseguenza se applico la conservazione della curvatura aggiungendo punti di flesso, lo dovrò fare sulle colonne, come mostrato in figura:
Ora ho sia la conservazione dell'angolo retto che della curvatura. Passo all'indeformata, riporto i tre flessi e disegno l'$M_{f}$ dalla parte delle fibre tese:
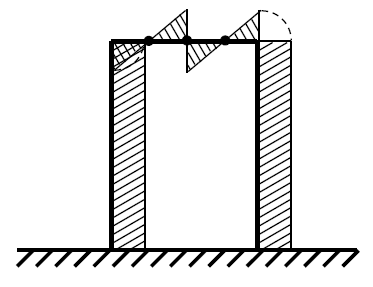
•Portale caricato da una coppia
In quest'ultimo esempio si ha una struttura simmetrica caricata da una coppia:
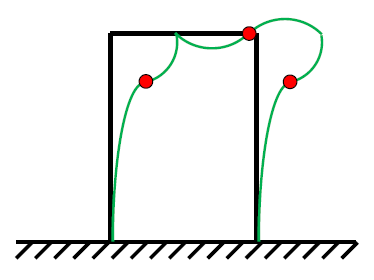
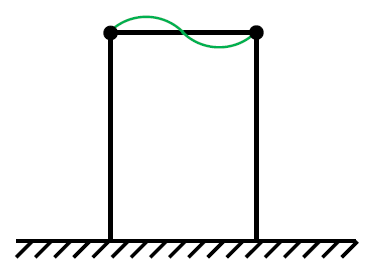
Si indebolisce la struttura introducendo due cerniere e si avrà la cosiddetta deformata ad S:
•Ora andiamo a vedere quanti flessi può avere una traversa caricata da una coppia. Sono in condizioni di antisimmetria perché la traversa è caricata in modo antisimmetrico.
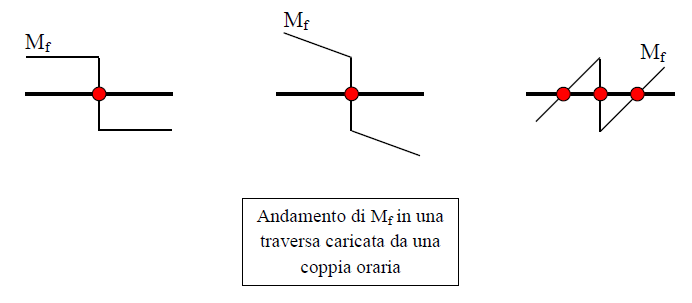
Per la regola del filo avrò le seguenti situazioni:
La traversa può avere o 1 flesso o 3 flessi (ed un flesso c'è già).
• La colonna, che non è caricata, può avere o 0 flessi o 1 flesso.
Si noti che ho la possibilità di inserire un flesso su entrambe le colonne oppure due flessi sulla traversa.
Ora c'è da capire se le colonne si inflettano andando un po' a destra o un po' a sinistra.
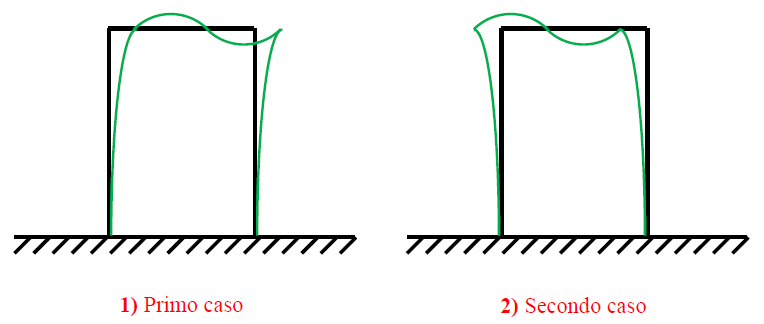
1) Primo caso: in questo caso c'è la conservazione della curvatura, ma dell'angolo retto sembrerebbe di no.
2) Secondo caso: in questa situazione c'è la conservazione dell'angolo retto, ma non della curvatura, quindi non va bene.
Ora mi chiedo com'è la deformata delle colonne e se ha qualche proprietà. Per scoprirlo introduco le reazioni vincolari sulla struttura: siccome la struttura è simmetrica, ma è caricata in modo antisimmetrico, mi aspetto che le reazioni vincolari siano di tipo antisimmetrico.
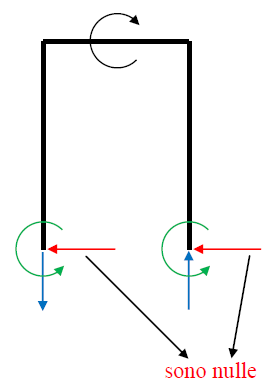
• Le reazioni di taglio sono uguali ed equiverse (altrimenti sarebbero simmetriche): poiché non equilibrate da nessun carico, dovranno essere nulle.
• Lo sforzo normale è come in figura dovendo essere antisimmetrico.
• Le coppie sono come in figura.
Ora andiamo a vedere com'è fatto l'$M_{f}$ sulle colonne: lo sforzo normale non dà $M_{f}$ perché agisce lungo l'indeformata.
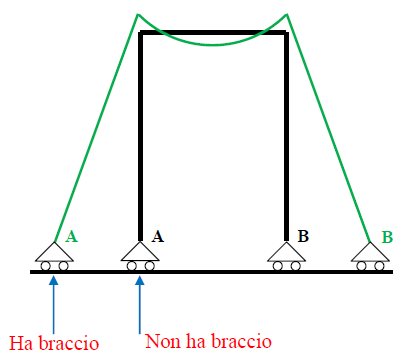
Infatti, se consideriamo una struttura labile orizzontalmente, essa si deformerà come in figura:
Dopo che i punti $A$ e $B$ si saranno aperti, in essi la reazione vincolare dà $M_{f}$ perché ha braccio. Se invece mi trovo sull'indeformata, le reazioni in $A$ e $B$ non daranno $M_{f}$ non avendo braccio.
Con l'esempio di struttura labile si vuole sottolineare che l'ipotesi di piccole deformazioni è importante: in sostanza l'equilibrio delle reazioni viene fatto sull'indeformata.
Le coppie danno $M_{f}$ sulle colonne, ma lo daranno uniforme. Quindi le colonne deformano ad arco di cerchio e non possono avere flessi. Ciò significa che non posso aggiungere un flesso sulla colonna.
Dall'analisi sulle reazioni vincolari si capisce che le colonne si dovranno inflettere verso sinistra.
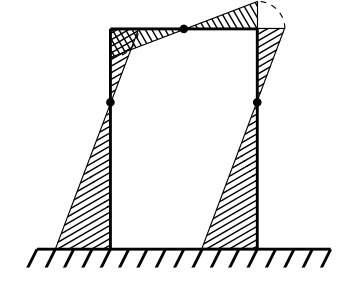
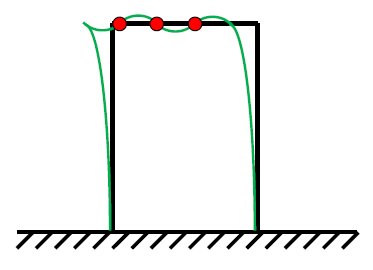
La deformata giusta presenterà quindi tre flessi sulla traversa:
Riportando l'$M_{f}$ dalla parte delle fibre tese otterrò il seguente diagramma: