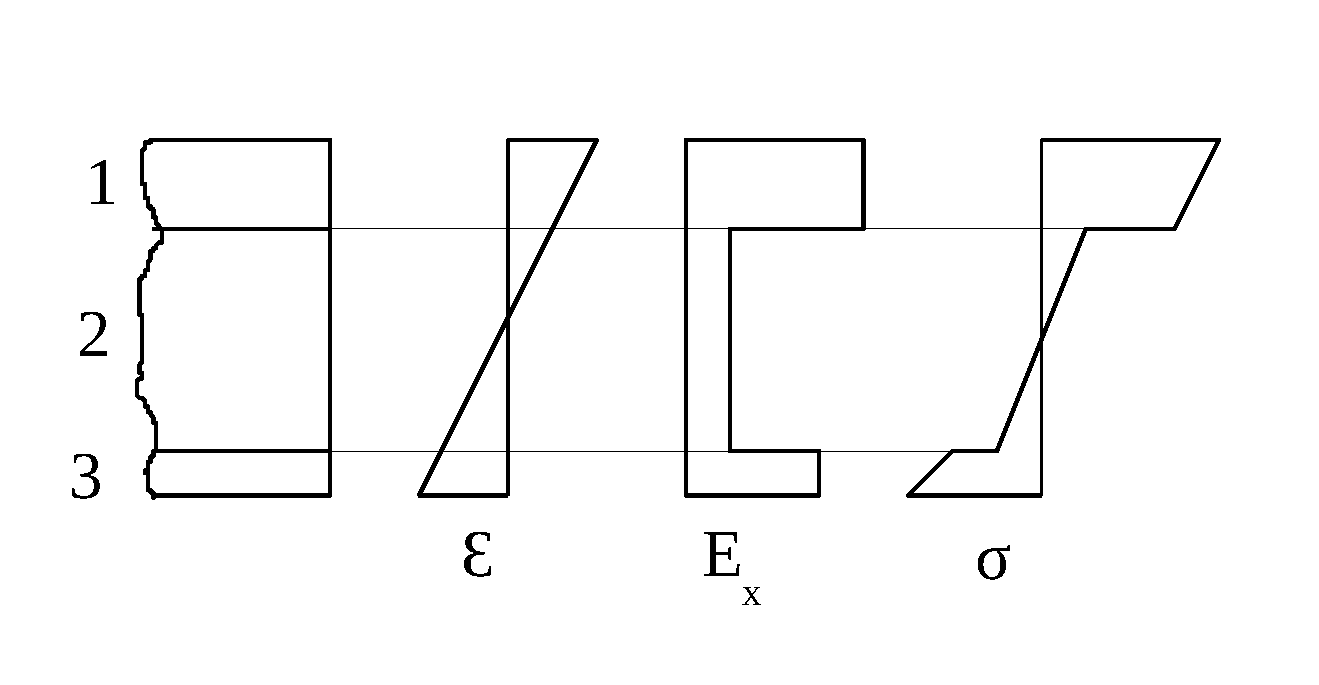Indice
Lezione 23: Teoria delle piastre
Introduzione e definizioni
- PIASTRA: corpo avente due dimensioni geometriche paragonabili, tra le quali può comunque essere scelta una lunghezza caratteristica, e una terza dimensione nettamente più piccola rispetto alle prime (spessore).
Per oggetti di questo tipo la teoria delle travi non è in grado di dare soluzioni accettabili al problema elastico: in altri termini, si otterrebbero errori macroscopici nel calcolo delle tensioni e delle deformazioni.
Occorre perciò utilizzare la teoria delle piastre, elaborata per studiare il comportamento di elementi elastici che hanno un piccolo spessore h, rispetto a una lunghezza caratteristica l.
Il rapporto h/l, sotto al quale è lecito usare tale approccio, è un numero puramente arbitrario: chi esegue l’analisi decide se accettare un errore più o meno grande, quindi se porre un rapporto h/l più o meno piccolo; più un corpo è tozzo (h/l tendente a 1) maggiori saranno gli errori forniti dalla teoria delle piastre.
Esempio:
\(\frac{h}{l}\ < \frac{1}{20}\ ; \hspace{2cm} \frac{h}{l}\ < \frac{1}{10}\ ; \hspace{2cm} \frac{h}{l}\ < \frac{1}{5}\)
- PIANO MEDIO: luogo dei punti medi dei segmenti paralleli allo spessore
- SUPERFICIE MEDIA: una qualunque superficie parallela al piano medio, dunque non necessariamente posta a metà dello spessore
Alle piastre viene assegnata una nomenclatura specifica:
- LASTRA: corpo di piccolo spessore caricato con azioni appartenenti al piano medio
- PIASTRA: corpo di piccolo spessore soggetto ad azioni anche non appartenenti al piano medio (es. momenti flettenti)
- GUSCIO: lastra/piastra di geometria non piana
In inglese non viene fatta distinzione tra piastra e lastra sulla base del tipo di caricamento, ma si usa il termine plate per entrambi i casi, mentre il guscio è denominato shell.
Convenzionalmente si costruisce un sistema di riferimento X,Y,Z dove gli assi X,Y individuano il piano medio, mentre l’asse Z indica la direzione dello spessore. Con tale sistema si definiscono:
- CARICHI PIANI: forze lungo X,Y (Fx, Fy)
- CARICHI FUORI DAL PIANO: forze lungo Z e momenti flettenti (Fz, Mx, Mx)
Inoltre
- u = spostamento in direzione X
- v = spostamento in direzione Y
- w = spostamento in direzione Z
Per convenzione le rotazioni sono considerate positive se di verso antiorario
Nella realtà le piastre possono avere spessori molto diversi e ciò può portare a comportamenti elastici differenti. Perciò sono state elaborate teorie apposite per casi specifici, seppur ideali.
La teoria che tratta gli elementi shell è estremamente complicata e non verrà affrontata. Tuttavia se la mesh di un guscio è sufficientemente fitta, la curvatura dei suoi elementi risulta trascurabile e pertanto possono essere assimilati a elementi di tipo piastra/lastra piana.
Teoria di Kirchhoff per le piastre Sottili
Ipotesi
- h < < < l, dove l è una dimensione caratteristica dell'intera piastra, non del solo concio elementare
- geometria piana
- carichi normali al piano medio
- i segmenti normali al piano medio nella configurazione indeformata, rimangono rettilinei e normali alla superficie elastica in configurazione deformata; come conseguenza, lo spessore non varia per ogni punto della piastra
- sollecitazioni a flessione prevalenti sul taglio, ovvero deformazione a taglio trascurabile; in virtù di ciò e della precedente ipotesi la piastra viene definita puramente flessionale o flesso-membranale
- nell'applicazione dei carichi flettenti si compiono piccole rotazioni, per cui si può assumere $ tg\theta = \theta$
- gli spostamenti in direzione Z sono sufficientemente piccoli per farli coincidere con lo spostamento della superficie media; da tale approssimazione deriva l’assunzione che questi spostamenti w sono costanti per ogni punto della struttura, ovvero sono indipendenti dalle deformazioni.
Secondo la teoria di Kirchhoff, gli spostamenti e le rotazioni di un punto della piastra possono essere calcolati tramite il moto della sua proiezione sul piano medio. In altri termini, lo spostamento complessivo (u,v) di un punto qualunque di una sezione di un concio di piastra è uguale allo spostamento del baricentro di questa sezione sommato allo spostamento dato dalle rotazioni della stessa.
Queste quantità sono definite come segue:
$w=w(x,y)$
$u=u_0+z \cdot \tan (\varphi_x) \approx u_0+z \cdot \varphi_x = u_0 - z \cdot \frac{\partial w}{\partial x} $
$v=v_0+z \cdot \tan (\varphi_y) \approx v_0+z \cdot \varphi_y = v_0 - z \cdot \frac{\partial w}{\partial y}$
$\varphi_x=-\frac{\partial w}{\partial x}$ = curvature flessionali
$\varphi_y=-\frac{\partial w}{\partial y}$ = curvature torsionali
Tuttavia è bene, come al solito, adimensionalizzare il problema ragionando sulle deformazioni, che otterremo grazie ai legami dati da un carico agente normalmente al piano medio.
Dalla quarta ipotesi discende che $\varepsilon_z =\gamma_{xz}=\gamma_{yz}=0$
Deformazioni
Risulta immediato calcolare le deformazioni:
$\varepsilon_x =-\frac{\partial u}{\partial x} = \frac{\partial u_0}{\partial x} - z \cdot \frac{{\partial}^{2} w}{{\partial x}^{2}}$
$\varepsilon_y =-\frac{\partial v}{\partial y} = \frac{\partial v_0}{\partial y} - z \cdot \frac{{\partial}^{2} w}{{\partial y}^{2}}$
$\gamma_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} = \frac{\partial u_0}{\partial y} + \frac{\partial v_0}{\partial x} - 2 z \cdot \frac{{\partial}^{2} w}{\partial x \partial y}$
Possiamo anche definire un vettore K delle curvature Ki
$K_x= -\frac{{\partial}^{2} w}{{\partial x}^{2}} ;\hspace{2cm} K_y= -\frac{{\partial}^{2} w}{{\partial y}^{2}} ;\hspace{2cm} K_{xy}= -\frac{{\partial}^{2} w}{\partial x \partial y} $
$$\underline{K}= \begin{bmatrix} K_x \\ K_y \\ K_{xy} \\ \end{bmatrix}$$
Il ridotto spessore della piastra le garantisce una forte rigidezza flessionale in quella direzione (asse Z), tanto da ritenere il problema sotto esame in tensione piana: le tensioni $\sigma_z$ perpendicolari al piano medio sono pertanto nulle.
Viene così spiegata l’ipotesi 5: le componenti deformative taglianti sono trascurabili.
Apparente contraddizione di ipotesi
Per l’ipotesi di tensione piana possiamo avere una libera deformazione in direzione Z, poiché non esistono tensioni che la ostacolino.
Tuttavia tra le ipotesi della teoria di Kirchhoff viene postulato che le sezioni perpendicolari al piano medio rimangono indeformate, dunque che non vi siano ad esempio strizioni in direzione Z.
Per far coesistere queste condizioni, in modo da usare la semplice matrice di tensione piana per esprimere il legame tensioni-deformazioni, si immagina di suddividere la piastra elementare in sezioni parallele al piano medio, di spessore infinitesimo e perciò in tensione piana, eliminando la continuità tra di esse. Successivamente si applicano i carichi, suddividendoli tra gli strati, e si calcolano le distribuzioni di tensioni e deformazioni: questi contributi verranno sommati in seguito, quando le sezioni saranno ricongiunte ripristinando la continuità materiale e degli spostamenti.
Siccome gli strati hanno spessore infinitesimo allora sono infinitamente rigidi in quella direzione, per cui si assume deformazione nulla normalmente al piano medio. Ricomponendo la piastra si otterrà pertando una deformazione $\varepsilon_z$ nulla, confermando l'ipotesi di Kirchhoff. Ma dato che le sezioni erano in tensione piana e la piastra non ha comunque un grande spessore, è ragionevole pensare che le tensioni rimangano nulle pure lungo tutto lo spessore di quest'ultima.
Tensioni
Assumiamo ora l’ulteriore ipotesi di ISOTROPIA DEL MATERIALE: stesso comportamento elasto-plastico in ogni direzione. In virtù di ciò possiamo legare le deformazioni alle tensioni attraverso un’unica matrice rigidezza, che chiameremo D.
$\underline{\sigma} = \underline{\underline{D}} \cdot \underline {\varepsilon} = \underline{\underline{D}} \cdot \underline {\varepsilon_0} + \underline {z} \cdot \underline{\underline{D}} \cdot \underline {k}$
$$\begin{bmatrix} \sigma_x \\ \sigma_y \\ \tau_{xy}\\ \end{bmatrix} = \frac {E}{1-{\nu}^{2}} \cdot \begin{bmatrix} \ 1 && \nu && 0 \\ \ \nu && 1 && 0 \\ \ 0 && 0 && \frac {1- \nu}{2} \\ \end{bmatrix} \begin{bmatrix} \ \varepsilon_x \\ \ \varepsilon_y \\ \ \gamma_{xy} \\ \end{bmatrix}$$
$$ \underline{\underline {D}} = \frac {E}{1-{\nu}^{2}} \cdot \begin{bmatrix} \ 1 && \nu && 0 \\ \ \nu && 1 && 0 \\ \ 0 && 0 && \frac {1- \nu}{2} \\ \end{bmatrix} $$
Flussi di sforzi e momenti
Dalle tensioni vogliamo ora passare ai carichi applicati, poiché lavorare con gli sforzi può portare ad ambiguità.
Si pensi ad esempio alla definizione di tensione normale:
$\sigma = \frac{F}{A}$
Quando si vuole ricavare la curva ingegneristica di un materiale, si considera $A = A_0$ che è l'area della sezione iniziale del provino, quindi costante. Tuttavia possono essere prodotte curve “tensione vera-deformazione vera”, in cui l’area è calcolata istante per istante.
A causa della strizione per effetto Poisson, la sezione reale sarà in ogni istante del caricamento più piccola di quella iniziale, dunque $\sigma$ sarà più grande.
Si deduce che uno stesso carico può fornire due valori diversi di tensione, a seconda della definizione usata, perciò per evitare ambiguità è meglio operare le analisi delle strutture usando direttamente le sollecitazioni applicate.
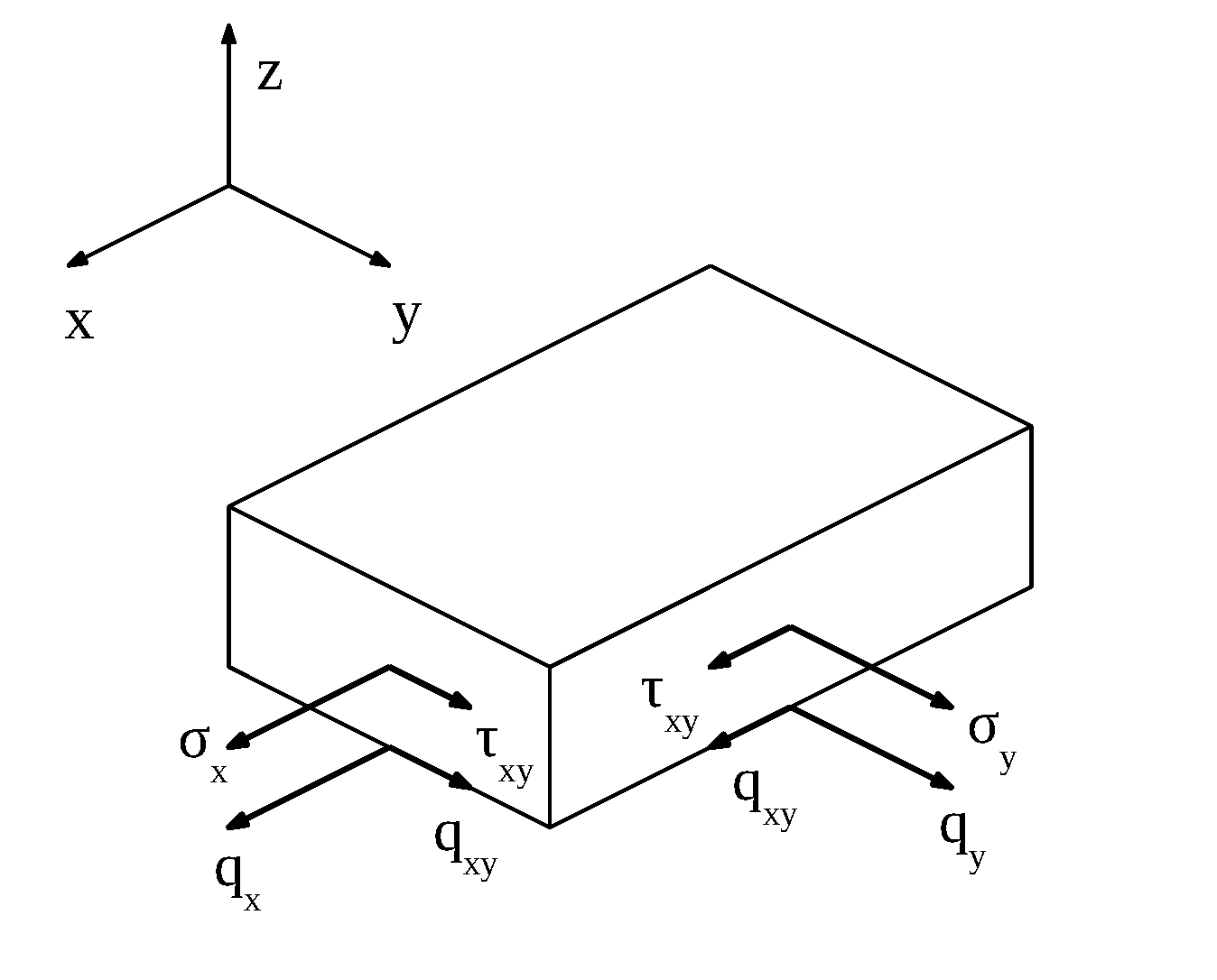
Per passare ai carichi (forze e momenti) prendiamo le distribuzioni di tensione sulle sezioni della piastra, assumendo una profondità unitaria, e le integriamo lungo lo spessore h.
Otteniamo così dei carichi per unità di lunghezza, chiamati FLUSSI DI SFORZI (q) e FLUSSI DI MOMENTI (m). In altri termini, vogliamo studiare come un elemento di piastra trasmette le sollecitazioni agenti su di esso agli elementi adiacenti, attraverso le interfacce comuni: le superfici. Uno studio analogo era già stato compiuto nella teoria delle travi, in riferimento ai conci elementari.
SFORZI
MOMENTI
$$\underline {q} = \begin{bmatrix} \ q_x\\ \ q_y \\ \ q_{xy}\\ \end {bmatrix} = \begin{bmatrix} \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_x \mathrm{d}z \\ \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_y \mathrm{d}z \\ \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \tau_{xy} \mathrm{d}z \\ \end{bmatrix} \begin{bmatrix} \ \frac{N}{mm} \\ \end{bmatrix}$$
$$\underline {m} = \begin{bmatrix} \ m_x\\ \ m_y \\ \ m_{xy}\\ \end {bmatrix} = \begin{bmatrix} \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_x \cdot z \mathrm{d}z \\ \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_y \cdot z \mathrm{d}z \\ \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \tau_{xy} \cdot z \mathrm{d}z \\ \end{bmatrix} \begin{bmatrix} \ \frac{N mm}{mm} \\ \end{bmatrix}$$
dove
- qi è prodotto da $\sigma_i$, mentre qij da $\tau_{ij}$
- mi è il momento agente sulla faccia perpendicolare all’asse i
- mij è generato da $\tau_{ij}$
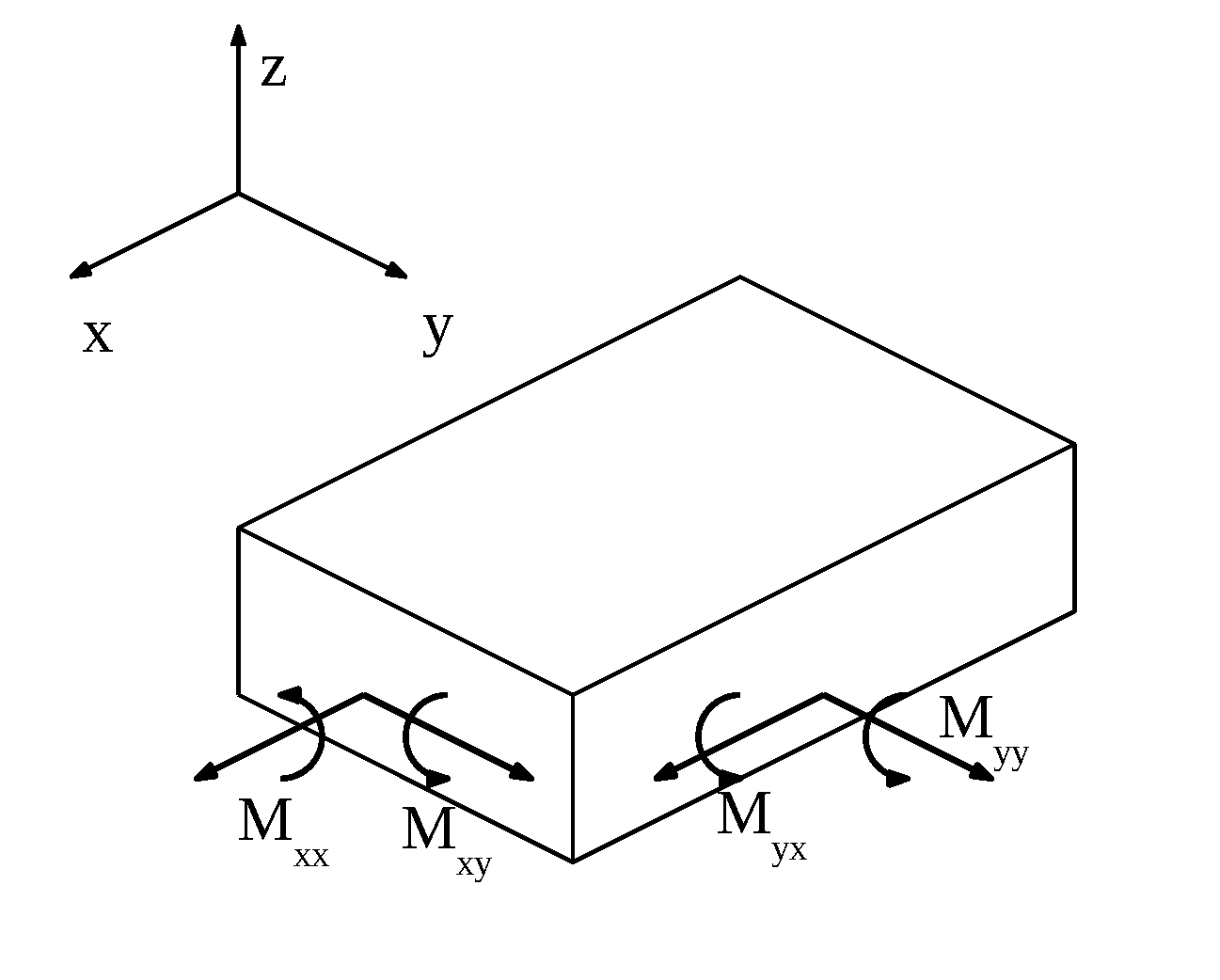
Ora ricaviamo da queste quantità i momenti agenti sulle facce degli elementi della piastra, orientati secondo gli assi del sistema di riferimento.
$m_x=M_{xy}$
$-m_{xy}=M_{xx}$
$-m_y=M_{yx}$
$m_{xy}=M_{yy}$
Dove con Mij si indica il momento applicato alla faccia ortogonale all’asse i, diretto secondo la direzione j.
Si nota dalle figure che i contributi Mxy e Myx sono FLESSIONALI, mentre Mxx e Myy esprimono contributi TORSIONALI.
In modo immediato si trovano le forze normali e taglianti:
$q_x= N_x$
$q_y= N_y$
$q_{xy}= T_{xy}$
Riassumendo in forma matriciale la relazione tra deformazioni e carichi:
$\underline{q} = \underline{\underline{A}} \underline{\varepsilon_0} + \underline{\underline{B}} \underline{k}$
$\underline{m} = \underline{\underline{B}} \underline{\varepsilon_0} + \underline{\underline{C}} \underline{k}$
$\underline{\underline{A}} = \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \underline{\underline{D}} \mathrm{d}z$
$\underline{\underline{B}} = \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \underline{\underline{D}} \cdot z \mathrm{d}z$
$\underline{\underline{B}} = \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \underline{\underline{D}} \cdot z^{2} \mathrm{d}z$
$$\begin{bmatrix} \ \underline{q} \\ \ \underline{m} \\ \end{bmatrix} = \begin{bmatrix} \ \underline{\underline{A}} && \underline{\underline{B}} \\ \ \underline{\underline{B}} && \underline{\underline{C}} \\ \end{bmatrix} \begin{bmatrix} \ \underline{\varepsilon_0} \\ \ \underline{k} \\ \end{bmatrix} $$
Le tre matrici A,B,C sono ottenute da D, matrice simmetrica; quindi sono anch’esse simmetriche.
- A: risultante delle forze legate alle deformazioni; esprime dunque il legame tra q ed $\varepsilon_0$
- C: risultante dei momenti legati alle curvature; esprime dunque il legame tra m e k
- B: matrice spuria, che accoppia la componente FLESSIONALE (legata a deformazioni ortogonali al piano medio) a quella MEMBRANALE (legata al piano medio)
Dato che il materiale è isotropo, D è funzione del modulo di Young (E) e del coefficiente di Poisson ($\nu$), non dello spessore h; ragion per cui può essere portata fuori dagli integrali, ottenendo
$\underline{\underline{A}} = h \cdot \underline{\underline{D}} $
$\underline{\underline{B}} = 0$
$\underline{\underline{C}} = \frac{h^{3}}{12} \cdot \underline{\underline{D}} $
$$\begin{bmatrix} \ \underline{q} \\ \ \underline{m} \\ \end{bmatrix} = \begin{bmatrix} \ h \cdot \underline{\underline{D}} && 0 \\ \ 0 && \frac{h^{3}}{12} \cdot \underline{\underline{D}} \\ \end{bmatrix} \begin{bmatrix} \ \underline{\varepsilon_0} \\ \ \underline{k} \\ \end{bmatrix} $$
Grazie alla simmetria dell’integrale la matrice B risulta nulla, per cui non esistono accoppiamenti flesso-membranali nella teoria di Kirchhoff. Si nota invece un legame lineare tra deformazioni e forze membranali, mentre la relazione tra momenti e deformazioni flessionali è cubica.
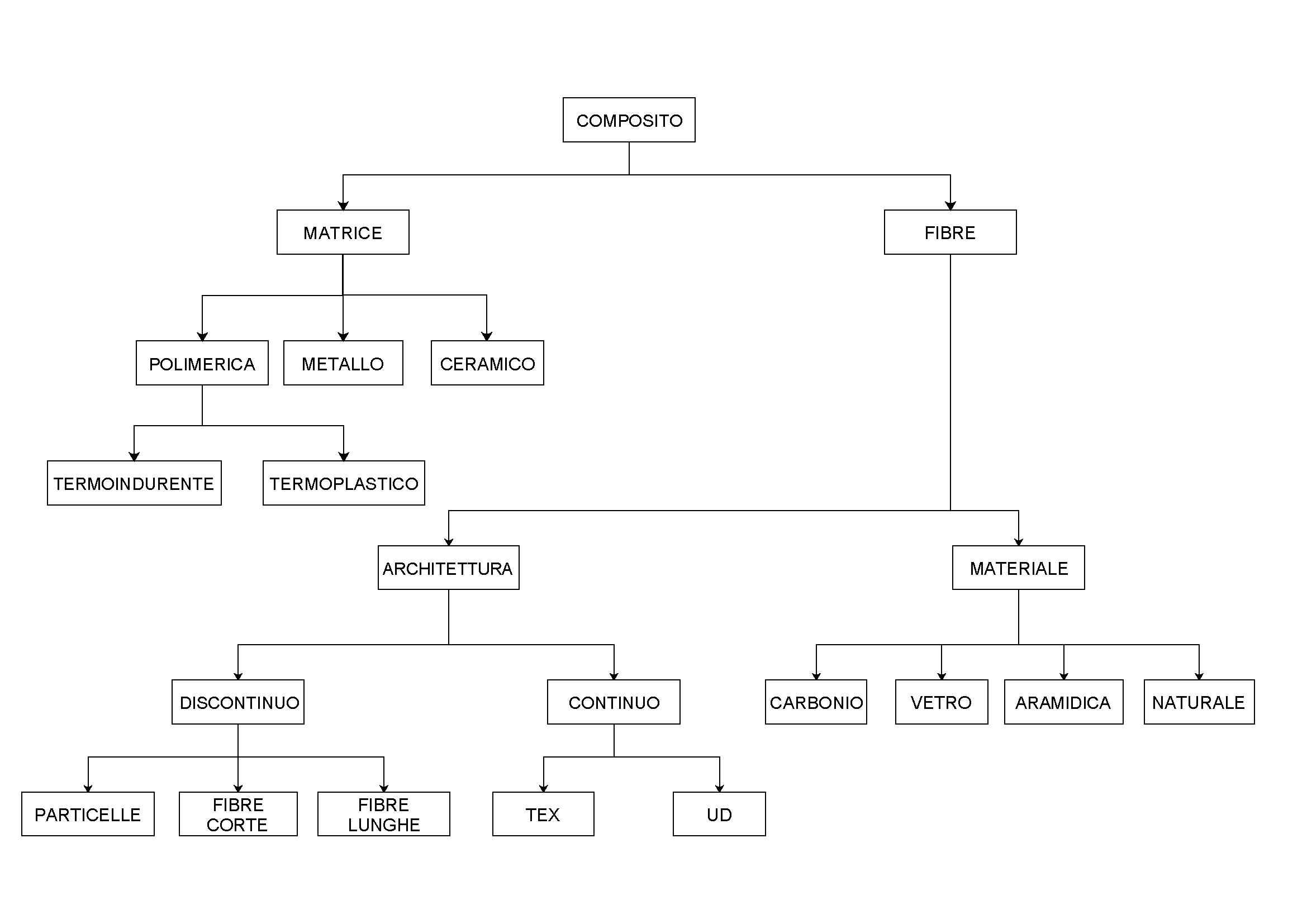
Esempio di ANISOTROPIA: materiali compositi
Materiale composito:
- sono presenti due o più fasi
- è possibile distinguerle, ovvero è presente una superficie di interfaccia tra esse
- sono chimicamente distinte (proprietà chimiche diverse)
- caratteristiche fisico-meccaniche differenti
I componenti di un materiale composito si distinguono principalmente in:
- RINFORZO: più resistente, in fase discontinua (fibre)
- MATRICE: minore resistenza meccanica, in fase continua
Nella matrice sono immersi i rinforzi e la sua continuità garantisce il passaggio del carico da una fibra isolata all’altra; in tal modo le tensioni non presentano discontinuità pericolose.
Le fibre possiedono una cosiddetta lunghezza efficace: la lunghezza oltre la quale le proprietà meccaniche non presentano miglioramenti signifcativi. Di solito si aggira attorno ai 5 cm.
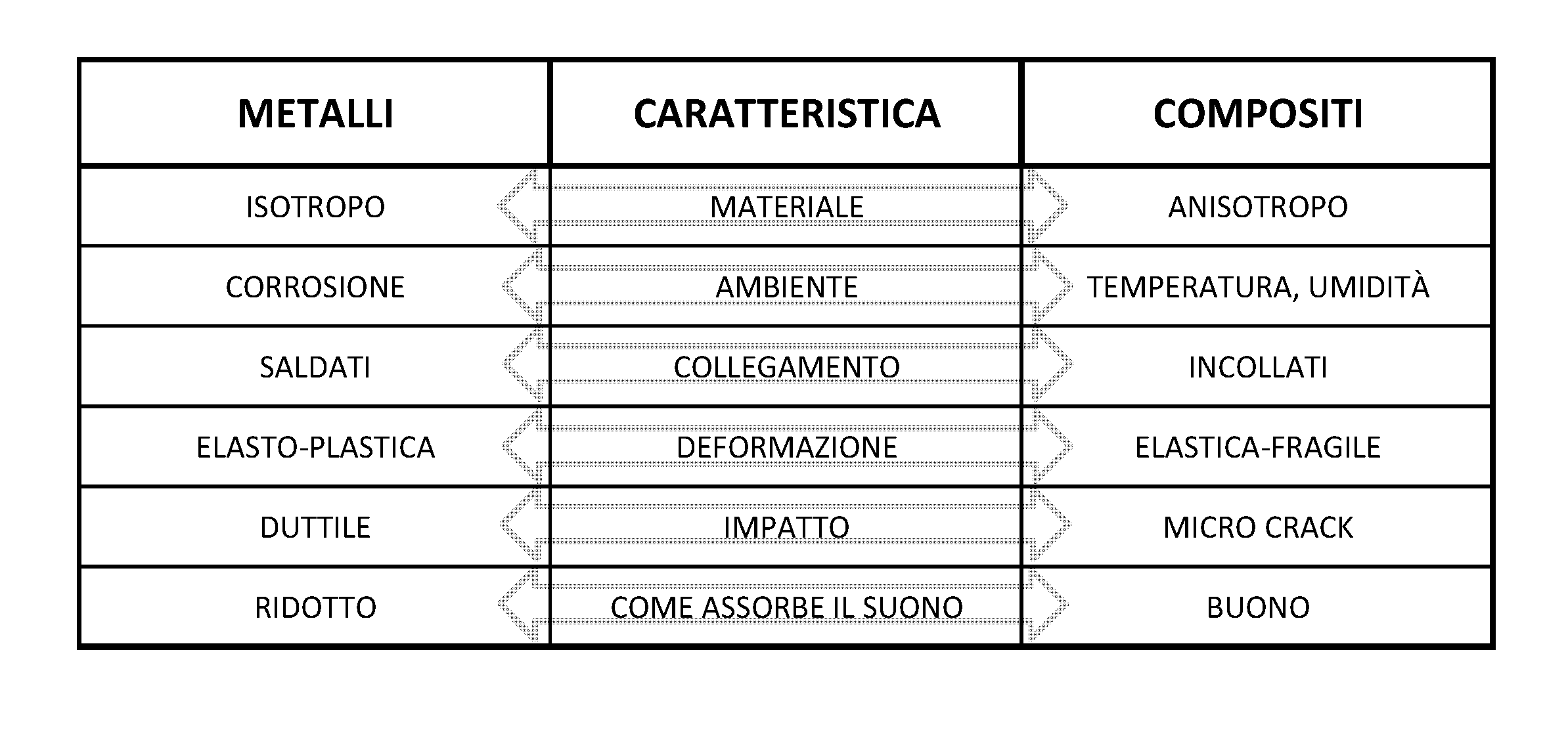
Si riporta di seguito una classificazione dei materiali compositi, seguita da una tabella comparativa delle loro proprietà con quelle dei metalli.
Si rimanda al pdf allegato “slide ing. Mantovani” per dettagli sui metodi/processi di produzione dei materiali compositi.
Tipi di anisotropia
- LAMINA ORTOTROPA: presenza di tre piani di simmetria ortogonali, che riduce a 9 le costanti elastiche caratteristiche.
- ISOTROPIA TRASVERSALE: le costanti elastiche scendono a 5.
Laminati
- LAMINATO: invece di avere una singola lastra ho un pacchetto di lamine (dette anche pelli), parallele al piano medio, di spessore hk e poste a distanza zk da esso.
Ipotesi della teoria classica dei laminati
- perfetto incollaggio delle lamine, ovvero continuità di spostamenti e deformazioni alle interfacce
- ipotesi della teoria di Kirchhoff per le lamine
Per calcolare la distribuzione delle tensioni, da integrare per trovare i carichi, bisogna considerare i contributi delle rigidezze di ogni pelle (Ex) e moltiplicarli per le deformazioni a cui ognuna è sottoposta. A causa infatti della continuità fisica delle lamine, che porta alla continuità degli spostamenti, le deformazioni sono continue lungo tutto lo spessore del laminato; tuttavia le singole lastrine possono essere fatte di materiali diversi, con diverse costanti elastiche.
Da tutto ciò si ottiene una discontinuità nel diagramma delle tensioni sulle sezioni del laminato.
Le tensioni hanno andamento lineare all’interno di ogni lamina, per cui possiamo ancora calcolare i flussi degli sforzi per ognuna di loro. I flussi totali agenti sul laminato saranno ottenuti dalla somma di questi appena trovati.
$N_i= \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_i \mathrm{d}z ; \hspace{2cm} M_i= \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_i \cdot z \mathrm{d}z ; \hspace{2cm} i=x,y,xy$
$$\begin{bmatrix} \ \varepsilon_x \\ \ \varepsilon_y \\ \ \gamma_{xy} \\ \ k_x \\ \ k_y \\ \ k_{xy} \\ \end{bmatrix} = \begin{bmatrix} \ A_{11} && A_{12} && A_{13} && B_{11} && B_{12} && B_{13}\\ \ A_{21} && A_{22} && A_{23} && B_{21} && B_{22} && B_{23}\\ \ A_{31} && A_{32} && A_{33} && B_{31} && B_{32} && B_{33}\\ \ B_{11} && B_{12} && B_{13} && C_{11} && C_{12} && C_{13}\\ \ B_{21} && B_{22} && B_{23} && C_{21} && C_{22} && C_{23}\\ \ B_{31} && B_{32} && B_{33} && C_{31} && C_{32} && C_{33}\\ \end{bmatrix} \begin{bmatrix} \ N_x\\ \ N_y\\ \ N_{xy} \\ \ M_x \\ \ M_y \\ \ M_{xy} \\ \end{bmatrix} $$
- A: matrice di rigidezza estensionale; lega le deformazioni nel piano con le tensioni nel piano.
- B: matrice di accoppiamento; lega le deformazioni nel piano ai momenti fuori dal piano e le rotazioni fuori dal piano alle tensioni nel piano
- C: matrice di rigidezza flessionale; lega le rotazioni fuori dal piano ai momenti fuori dal piano
Tipi di laminati
1) Laminati SIMMETRICI: B=0
Per questa classe di laminati l'accoppiamento tra flessione e sforzo normale è assente.
Le lamine sono disposte simmetricamente rispetto al piano medio; tale simmetria è di carattere sia geometrico che elastico, ovvero due lamine a distanze opposte dal piano medio hanno le stesse proprietà elastiche.
Da ciò discende che nella matrice B ci saranno contributi opposti, che rendono nulli i suoi elementi.
Ciò risulta molto vantaggioso durante la cura della resina: quando raffreddo si generano delle tensioni interne nel piano del laminato, ma se B non è nulla esse producono deformazioni fuori piano (svergolamenti, ingobbamenti). Per questa ragione i laminati simmetrici sono molto usati.
Convenzionalmente si identifica un laminato indicando una successione di angoli, che esprimono l’orientamento delle fibre delle singole lamine (o pelli) rispetto a quelle esterne.
Un esempio di questa nomenclatura:
0°\0°\+45°\-45°\-45°\+45°\0°\0°
o in forma semplificata
$\begin{bmatrix}
\ 0_2 / \pm 45°
\end {bmatrix}_S$
Come si può notare, un laminato simmetrico deve avere per ogni lamina sopra (o sotto) al piano medio un'altra lamina di uguale geometria, con identico orientamento.
2) Laminati ORTOTROPI o BILANCIATI: $A_{13}=A_{23}=0$
La caratteristica primaria di questi laminati è il disaccoppiamento tra sforzo normale e scorrimenti, ovvero tra taglio e deformazioni normali. Ciò si realizza se i termini $A_{13}=A_{23}=0$, che risultano dalla sommatoria estesa alle lamine degli omologhi termini della matrice del legame costitutivo; siccome questi ultimi sono funzioni dispari dell'angolo di orientazione $\alpha$, si potranno annullare solo se per ogni pelle disposta con angolo $\alpha$, ne esiste una di angolo $–\alpha$ indipendentemente dalla sequenza.
E' possibile costruire laminati sia simmetrici che bilanciati disponendo le lamine di ciascuna metà in modo che si bilancino, mantenendo poi la simmetria tra le metà. Un esempio di laminati di questo tipo è
$\begin{bmatrix}
\ 0_2 / \pm 45°
\end {bmatrix}_S$
3) Laminati con $D_{13}=D_{23}=0$
Essi realizzano il disaccoppiamento tra momenti flettenti e curvatura torsionale, ovvero tra momenti torcenti e curvature flessionali.
Tale condizione si realizza solo se $D_{13}=D_{23}=0$, ma con alcuni passaggi algebrici è possibile dimostrare che i laminati simmetrici non posso soddisfarla, dato che gli omologhi termini della matrice del legame costitutivo saranno uguali e non nulli. Per annullarli bisognerebbe disporre sopra e sotto il piano medio lamine con orientamento opposto, compromettendo la simmetria.
La soluzione al problema consiste nel disporre le lamine successive con orientamento opposto: in questo modo si può rispettare la simmetria (una condizione sempre desiderata) e si otterranno $D_{13}$ e $D_{23}$ quasi nulli, dunque un disaccoppiamento tra flessione e torsione pressoché totale.
Il laminato
$\begin{bmatrix}
\ 0_2 / \pm 45°
\end {bmatrix}_S$
realizza anche questa condizione.
4) Laminati QUASI ISOTROPI: non sono isotropi ma la matrice A è isotropa
In altri termini, la loro rigidezza estensionale è indipendente dal particolare orientamento considerato.
Ciò si verifica se accade che:
- il numero di lamine $n\geq 3$
- le lamine devono essere uguali per lo spessore e il materiale
- le lamine sono equispaziate angolarmente: $\Delta \theta = \frac{2\pi}{n}$
NOTA: La denominazione di laminato quasi isotropo è legata al fatto che essi hanno comportamento isotropo solo rispetto alla trazione-compressione e non rispetto a flessione e torsione, essendo in generale le matrici B e D non isotrope.
Esempio: 12 pelli:
$\begin{bmatrix}
\pm 30°/ \pm 90°/ \pm 30°
\end {bmatrix}_S$
Nella pratica costruttiva i laminati quasi isotropi sono poco impiegati, poiché non soddisfano lo scopo principale dell'uso dei laminati: sfruttare la loro anisotropia attraverso l'opportuna orientazione delle lamine, per avere la massima resistenza nella direzione delle sollecitazioni massime.
Classificazione strutturale
- PIASTRE SOTTILI (Kirchhoff): spessore piccolo, garantisce rigidezza flessionale
- PIASTRE SPESSE (Mindlin): non posso trascurare le deformazioni di taglio
Un esempio di questa distinzione si riscontra nelle travi: se in sede di una prova flessionale gli appoggi sono abbastanza vicini al carico centrale, allora le componenti di taglio non sono più trascurabili.
Si ricordi comunque che la teoria di Mindlin è applicabile a piastre di medio spessore, per le quali il rapporto h/l è ancora abbondantemente minore dell'unità. Le piastre di grosso spessore forniscono problemi anche con questo approccio.
- GUSCI/MEMBRANE: piastre curve, spessore piccolo; gli sforzi membranali sono rilevanti
- PIASTRE CURVE DI GRANDE SPESSORE: non si può trascurare alcun tipo di sollecitazione
Appendice: Collasso nodale
Un caso particolare è rappresentato dalla saldatura di testa di due piastre: se andiamo a modellarle usando i piani medi, ai quali assegniamo i rispettivi spessori oltre a tutte le condizioni al contorno, ci accorgiamo che nel punto della giunzione i piani non entrano in contatto, a causa degli spessori. In altre parole, i nodi terminali dei piani medi restano separati e lasciano un vuoto inaccettabile per il calcolo FEM.
Il problema si risolve in due modi:
- Link rigido tra i nodi attraverso un RBE2
- Faccio collassare i due nodi in uno unico
Bibliografia
- B.Zuccarello - Progettazione meccanica con materiali non convenzionali - Capitolo 5: Laminati compositi; http://imechanica.org/files/Cap5.pdf