DINAMICA DI SISTEMI AD n GDL (FEM)
(vedi anche https://cdm.ing.unimo.it/files/progettazione_assistita/materiale_didattico/mia_dispensa_dinamica_bozzabozzabozza.pdf)
Forma di equilibrio dinamico:
$\underline{\underline{M}} \ddot{\underline{x}} + \underline{\underline{C}} \dot{\underline{x}} + \underline{\underline{K}} \underline{x} = \underline{F}(t)$
- $\underline{\underline{M}} = \text{matrice massa}$
- $\underline{\underline{C}} = \text{matrice smorzamento}$
- $\underline{\underline{K}} = \text{matrice rigidezza}$
Con ipotesi di comportamento lineare del sistema con soluzioni periodiche scomposte in serie di Fourier (per trovarne la forma armonica) siamo giunti alla forma algebrica dell'equazione differenziale sopra citata ponendo:
$ \underline{x} (t)= Re(\overline{\underline{x}}e^{j\omega t}) \Rightarrow \dot{x}=j \omega \overline{x} e^{j\omega t} \Rightarrow{\ddot{x}=-\omega^2 \overline{x} e^{jwt}}$
$F(t)=\underline{\overline{f}}e^{j\omega t}$
$(-\omega^2 \underline{\underline{M}} + j \omega \underline{\underline{C}} + \underline{\underline{K}}) \underline{\overline{x}} = \underline{\bar{f}}$
Dove:
- $\underline{x}$ = numero complesso che contiene componente reale ed immaginaria delle armoniche di risposta
- $\underline{f}$ = forzante esterna in forma complessa
Tramite questa equazione ricavo $\underline{\overline{x}}$; dopodiché so che ogni elemento del vettore è:
$x(t) = Re(\, \overline{x} \, e^{j \omega t} \,) \quad \text{con} \quad \omega = 2\, \pi \, \mathsf{f} \quad \: \text{ove} \quad \mathsf{f}=\text{frequenza}$
Considero ora alcune soluzioni particolari cioè mi chiedo se esistano modi di oscillare che siano soluzioni armoniche non banali associate a forzante esterna nulla ; perciò mi chiedo se il sistema stia fermo in assenza di forzante oppure no
$\underline{\overline{f}} = \underline{0}$
Affinché possa pensare di avere soluzioni non banali (diverse dalla stasi) devo eliminare ogni elemento dissipativo del sistema altrimenti il moto non può proseguire in eterno, perciò:
$\underline{\underline{C}} = \underline{\underline{0}} \quad \text{matrice nulla}$
Quindi il problema algebrico si riduce nella forma:
(-$\omega^2 \underline{\underline{M}} + \underline{\underline{K}}) \underline{\overline{x}} = \underline{0}$
dove il termine moltiplicativo di $\underline{\overline{x}}$ viene chiamato MATRICE DI SISTEMA.
Nel caso in cui la matrice di sistema abbia rango pieno ho un'unica soluzione ovvero $\underline{\overline{x}}=\underline{0}$ quindi solo la soluzione banale che non si vuole considerare; perciò considero forme singolari della matrice di sistema del tipo:
$ \mathsf{det}(- \omega^2 \underline{\underline{M}} + \underline{\underline{K}}) = 0$
Sapendo che La matrice massa $\underline{\underline{M}}$ è costante così come la matrice K (per l'ipotesi di linearità assunta), l'annullamento del determinante è legato al termine $\omega^2$
- $\underline{\underline{K}}$è una matrice semi-definita positiva (definita positiva nel caso in cui sistema vincolato)
- $\underline{\underline{M}}$ è una matrice sempre definita positiva (di conseguenza -M è definita negativa)
Perciò nella formula precedente una matrice definita negativa è aggiunta ad una matrice definita positiva in quote crescenti dovute alla pulsazione della eccitante cioè $\omega$ (in questo caso non avendo eccitante esterna, la pulsazione è quella della risposta, viene quindi definita pulsazione naturale del sistema).
Quindi si ha un'equazione nell'incognita $\omega^2$ e tipicamente il determinante è un polinomio di grado n dove n è l'ordine della matrice di sistema (nella maggior parte dei casi il polinomio è di grado elevato perciò non è possibile trovarne una soluzione analitica ma si procederà con processi iterativi).
Nel caso in cui si riuscisse a trovare delle soluzioni $\omega_i^2$ con det=0 allora insieme alla soluzione banale si avranno anche delle oscillazioni con pulsazioni $\omega_i$ che possono esistere senza la presenza di forzanti esterne al sistema.
Sostituendo gli $\omega_i$ trovati nell'equazione:
(-$\omega^2 \underline{\underline{M}} + \underline{\underline{K}}) \underline{\overline{x}} = \underline{0}$
è possibile calcolare una componente del vettore $\underline{\overline{x}}_i$ per ogni $\omega_i$ che è soluzione che si aggiunge a quella banale.
Perciò si hanno coppie $\omega_i$,$\underline{x}_i$ che rappresentano moti propri del sistema senza eccitante esterna dove gli $\omega_i$ sono definiti come pulsazioni proprie del sistema.
In realtà il sistema è singolare perché per trovare le pulsazioni proprie del sistema è stato imposto che il determinante della matrice di sistema abbia determinante nullo perciò per trovare le soluzioni volute $\omega_i$ occorre moltiplicare l'equazione per l'inversa della matrice $\underline{\underline{M}}$ ottenendo:
$(-\omega^2 \underline{\underline{I}} + \underline{\underline{M}}^{-1} \underline{\underline{K}}) \underline{\overline{x}}= \underline{0}$
che è ha la forma di un problema agli autovalori:
$(\underline{\underline{A}} - \lambda \underline{\underline{I}})\underline{v}=0$
Ricorda un problema di ricerca di coppie di autovalori-autovettori dove la generica soluzione $\lambda_i$ è autovalore (detto anche eigenvalue) e $\underline{v}_i$ è l'autovettore (detto anche eigenvector) associato.
i generici $\lambda_i$ sono soluzioni della forma:
$ \mathsf{det}(\underline{\underline{A}} - \lambda \underline{\underline{I}})=0$
Che è un polinomio di grado n dove n è l'ordine della matrice $\underline{\underline{A}}$ o $\underline{\underline{I}}$
- Se $\lambda_i$ ha molteplicità = 1 –> ha un solo autovettore associato
- Se $\lambda_i$ ha molteplicità > 1 –> avrà numero di autovettori associati pari al valore della sua molteplicità
Il problema di come si trovino le varie coppie $\lambda_i$ , $\underline{v}_i$ non lo poniamo perché lasciamo ad un codice apposito il calcolo; perciò si suppone di avere la soluzione già a disposizione.
Nel nostro caso $\lambda_i$ coincide con $\omega^2_i$.
In realtà si cerca di non invertire la matrice M perché è molto grande perciò richiederebbe un'elevata complessità di calcolo perciò alcuni algoritmi risolvono automaticamente:
$\mathsf{det} (\underline{\underline{A}} - \lambda \underline{\underline{I}})=0$
Tornando all'equazione:
(-$\omega^2 \underline{\underline{M}} + \underline{\underline{K}}) \underline{\overline{x}} = \underline{0}$
Le coppie $\lambda_i$ , $\underline{v}_i$, che nel nostro caso particolare sono $\omega^2_i$ e $\underline{\overline{x}}_i$, permettono di trovare la legge di moto del sistema cioè lo spostamento in funzione del tempo in assenza di sollecitazioni esterne:
$\underline{x}(t)=Re(\underline{\overline{x}}_i e^{j \omega_i t}) $
Nella realtà ogni sistema è sempre composto da dissipazioni seppur piccole perciò questi fenomeni non sono mai visibili.
La singolarità della matrice di sistema ammette la presenza di almeno $\infty^1$ soluzioni (se la matrice ha rango n-1) ciò vuol dire che se $\underline{\overline{x}}_i$ è un autovettore allora anche un generico $\lambda \underline{\overline{x}}_i$ è soluzione dove $\lambda$ è uno scalare arbitrario perciò ho moti con ampiezza indefinita.
Nel caso in cui siano presenti più autovalori di pari valore (cioè $\omega_i^2$ con molteplicità>1) per esempio:
$\omega_i^2$ con molteplicità 3 a cui sono associati $\underline{\overline{x}}_{i1}$ , $\underline{\overline{x}}_{i2}$ , $\underline{\overline{x}}_{i3}$
allora è soluzione del problema anche una qualunque combinazione lineare dei 3:
$\lambda_1 \underline{\overline{x}}_{i1} +\lambda_2 \underline{\overline{x}}_{i2} + \lambda_3 \underline{\overline{x}}_{i3}$
Che rappresenta un altro moto che esiste in assenza di forzante, si ha la possibilità di operare su tre parametri indipendenti rimanendo nel campo delle soluzioni di $\mathsf{det}(\underline{\underline{A}} - \lambda \underline{\underline{I}})=0$
[Se $\omega_i^2$ ha molteplicità 3 allora -$\omega^2 \underline{\underline{M}} + \underline{\underline{K}}$ è una matrice di rango n-3 quindi $\infty^3$ soluzioni].
Consideriamo ora un caso specifico:
Barra flettente incastrata ad un estremo
3 GDL per nodo (cioè spostamenti e rotazioni)
Nella struttura discretizzata a FEM ho 6 nodi non vincolati ciò vuol dire che ho 18 GDL totali quindi le matrici massa $\underline{\underline{M}}$ e rigidezza $\underline{\underline{K}}$ sono 18×18.
La struttura avrà tanti modi propri di vibrare quanti sono i GDL della struttura, dopo un certo valore però le frequenze raggiunte sono talmente elevate da poter non essere più considerate; perciò prendo in considerazione solo i primi modi propri cioè quelli confinati ai valori di frequenza più bassi (cioè $\omega_i$ minori) che sono i più importanti perché condizionano maggiormente il moto della struttura.
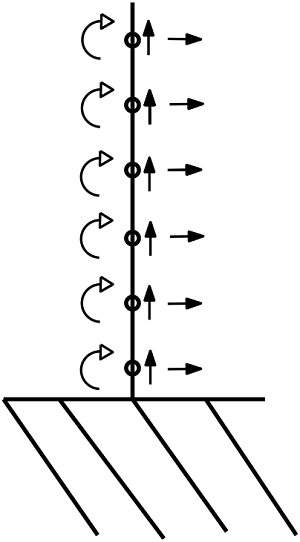
I° modo proprio di vibrare della struttura cioè quello a pulsazione $\omega_i$ più bassa
Il generico nodo ha rotazione diversa da zero, spostamento nullo lungo y ma diverso da zero lungo x perciò un generico autovettore associato a questo modo proprio di vibrare è:
$$ \newcommand{\vec}[1]{\smash{\underline{#1}}} \newcommand{\mat}[1]{\smash{\underline{\underline{#1}}}} $$ $$ \underline{\overline{x}}_i = \begin{bmatrix} ...\\ ...\\ \delta\\ 0\\ \theta\\ ...\\ ...\\ \end{bmatrix} $$
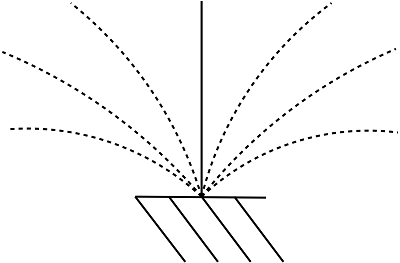
Dove i valori di $\delta$ e $\theta$ sono quelli attribuiti al generico nodo ma cambieranno da nodo a nodo pur mantenendo lo spostamento y sempre nullo. Il vettore $\underline{\overline{x}}_i$ indica l'ampiezza dello spostamento dovuto a quel generico modo di vibrare della struttura. Ovviamente saranno possibili tutte le possibili ampiezza definite da $\lambda \underline{x}_i$ con $\lambda$ scalare qualsiasi. Cioè posso trovare, per scalatura, tutte le deformate del tipo:
In realtà vorrei trovare una soluzione sola per ogni modo di vibrare della struttura cioè un unico vettore $\underline{x}_i$, perciò devo trovare un $\lambda$ che soddisfi la relazione:
$\lambda \underline{\overline{x}}_i^T \underline{\underline{M}} \lambda \underline{\overline{x}}_i=1$
dove indico:
$\lambda \underline{\overline{x}}_i = \underline{\hat{x}}_i$ Scalatura a massa unitaria di $\lambda$
Perciò vengono restituiti $\lambda \underline{\overline{x}}_i$ che rispettano quella scalatura e vengono accettati come soluzione unica in $\underline{\hat{x}}_i$.
Ora riprendo il caso originario considerando anche la smorzamento
(-$\omega^2_i \underline{\underline{M}} + j \omega_i \underline{\underline{C}} + \underline{\underline{K}}) a \underline{\hat{x}}_i = \underline{\bar{f}}$
Suppongo di eccitare il sistema con una pulsazione pari ad una delle pulsazioni naturali $\omega_i$ del mio sistema e verifico se esiste una forma del tipo a$\underline{\hat{x}}_i$ (scalatura arbitraria del modo proprio) che può essere soluzione per un qualche valore di “a”.
(-$\omega^2_i \underline{\underline{M}} + j \omega_i \underline{\underline{C}} + \underline{\underline{K}}) a \underline{\hat{x}}_i = \underline{\bar{f}}$
Posso scriverla come:
(-$\omega^2_i \underline{\underline{M}} + \underline{\underline{K}}) a\underline{\hat{x}}_i + j \underline{\omega_i} \underline{\underline{C}} a \underline{\hat{x}}_i = \underline{\bar{f}}$
Dove (-$\omega^2_i \underline{\underline{M}} + \underline{\underline{K}}) a\underline{\hat{x}}_i =0$ per definizione, perché la frequenza considerata è pari ad una pulsazione naturale del sistema.
$j \underline{\omega_i} \underline{\underline{C}} a \underline{\hat{x}}_i = \underline{\bar{f}}$
La forzante esterna è equilibrata dal termine smorzante con pulsazione $\omega=\omega_i$ cioè pulsazione naturale del sistema.
Quindi abbiamo ottenuto un'equazione vettoriale in un'incognita cioè “a”.
Premoltiplico per $\underline{\hat{x}}_i^T$ per ottenere un'equazione scalare:
$j\omega_i\underline{\hat{x}}_i^T\underline{\underline{C}}\underline{\hat{x}}_ia=\underline{\hat{x}}_i^T\underline{\bar{f}}$
Da questa equazione scalare posso calcolare “a”:
$a=\underline{\hat{x}}_i^T\underline{\bar{f}}/j\omega_i\underline{\hat{x}}_i^T\underline{\underline{C}}\underline{\hat{x}}_i$
“a” rappresenta l'ampiezza con cui il modo proprio di vibrare può sussistere nella struttura con forzante esterna e smorzamento.
Si può notare che il modulo di “a” è definito dal rapporto di due entità:
- Numeratore –> $\underline{\hat{x}}_i^T\underline{\bar{f}}$
- Denominatore –> $\underline{\hat{x}}_i^T\underline{\underline{C}}\underline{\hat{x}}_i$
Quindi se $\underline{\hat{x}}_i^T\underline{\bar{f}}=0$ –> a=0 Perciò è sufficiente che $\underline{\hat{x}}_i^T$ sia perpendicolare ad $\underline{\bar{f}}$ per far annullare “a”.
Diapason
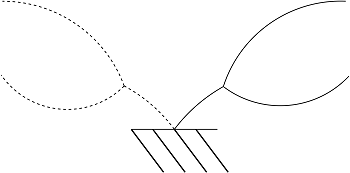
Un diapason nello spazio ha una varietà di modi propri pari al numero di nodi in cui è discretizzato per 6 gradi di libertà, ogni nodo considerato con traslazioni e rotazioni nulle. Se il diapason non fosse discretizzato, ma venisse considerato un materiale continuo, i suoi modi propri sarebbero infiniti. Considero il caso in cui il diapason ha solo due modi propri di vibrare. Il primo modo proprio è la vibrazione in apertura e chiusura delle aste in direzione simmetrica, di solito con una frequenza di 440Hz. Il punto inferiore che congiunge i due rami e la barra incastrata sono fermi.
Il secondo modo proprio del diapason incastrato alla base è un moto di oscillazione.
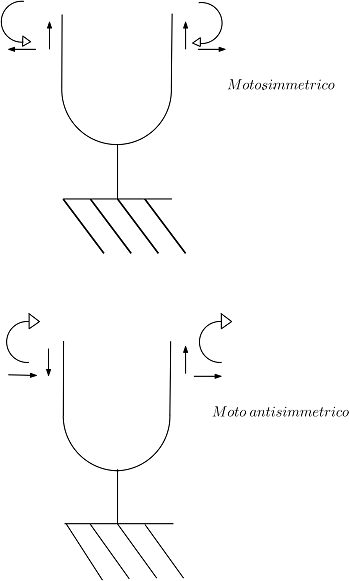
Se la struttura è simmetrica, come nel caso del diapason, i modi propri possono essere di tipo simmetrico o antisimmetrico. Nei modi simmetrici gli spostamenti normali al piano di simmetria sono uguali e contrari, gli spostamenti paralleli al piano sono uguali e le rotazioni con asse parallelo all'asse di simmetria sono uguali e opposti. Nel caso opposto il modo è di tipo antisimmetrico.
Applichiamo una forza simmetrica sui due bracci del diapason di entità Fcosωt con pulsazione propria. Nel caso in esame interessano soltanto le prime 6 componenti dei vettori.
INSERIRE VETTORI
Il prodotto scalare al numeratore fra i vettori xi cappuccio e F è nullo perché i vettori sono ortogonali. Il vettore velocità è proporzionale al vettore spostamento e la potenza istantanea è il prodotto istantaneo fra forza e velocità. Se i due vettori sono ortogonali, il loro prodotto scalare è nullo. Se il numeratore è nullo, l'identità di a tende ad un valore infinito, ciò si ha nel caso di smorzamento prossimo a zero. In generale tutti i sistemi di forza antisimmetrici non possono compiere lavoro sui modi simmetrici e tutti i sistemi di forze simmetrici non possono compiere lavoro sui modi antisimmetrici.
Nel caso di lievi deformazioni della simmetria, per esempio nel caso di diapason storto, il prodotto scalare xi cappuccio F sarebbe diverso da zero, con un'entità tanto grande quanto maggiore è la deformazione. Il sistema in questo caso particolare ha una soluzione periodica di ampiezza infinita, cioè ciclo dopo ciclo la forza eccitante introduce nel sistema un lavoro che si accumula e il sistema inizia a vibrare con energia sempre maggiore.
Il denominatore si annulla quando le forze viscose sono ortogonali al modo di vibrare, nell'esempio del diapason questo caso si verifica quando lo si sorregge con le mani, perché non è un incastro perfetto, ma fungono da smorzatore. La matrice smorzamento non è più nulla e la soluzione a lungo termine non ha più ampiezza infinita.
Proprietà dei modi propri
1) due modi propri, xi cappuccio e xj cappuccio, sono ortogonali rispetto alla matrice massa quando
xj cappuccio matrice M xi cappuccio = delta ij di Kronecker con delta ij = 0 se i diverso da j e 1 se i=j
2) due modi propri sono ortogonali rispetto alla matrice rigidezza quando
xj cappuccio matrice K xi cappuccio = 0 se i diverso da j e ω^2 se i=j
se sono soddisfatte entrambe le condizioni allora i due modi propri sono linearmente indipendenti.
Considero un pendolo vibrante nel piano ad una certa frequenza, a seconda del piano considerato ho dei modi propri diversi e indipendenti, ma con la stessa frequenza.
IMMAGINE PENDOLO
Siano ω1xicappuccio1 e ω1xicappuccio2 i due modi propri del pendolo, è possibile tracciare i modi propri del sistema all'interno di un piano xz. Componendo i modi propri di ciascun piano si può ottenere degli ulteriori modi piani e a seconda del parametro di composizione, è possibile variare anche la fase ed ottenere, per esempio, un modo ellittico o circolare.
IMMAGINE.