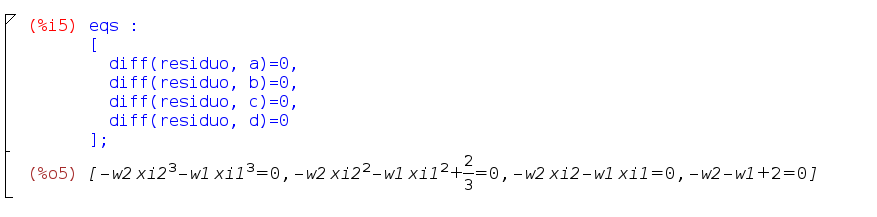Sono stati introdotti nuovi comandi che consentono un utilizzo più efficace e completo del manipolatore algebrico:

ratsubst(a,b,c)

Sostituisce a al posto di b nella formulazione c e mostra l'espressione risultante.

assume 
forget

assume memorizza delle istruzioni che, a meno che non siano inconsistenti o ridondanti, sono mantenute in considerazione nel corso delle formulazioni successive. In tal modo è possibile, ad esempio, far sapere al software che una data variabile è positiva e quindi non necessita l'applicazione del modulo. Con forget invece maxima dimentica l'istruzione data.

makelist(espres,x,x_0,x_max,passo)

Genera una lista di elementi secondo la funzione specificata come primo argomento nella variabile indipendente indicata al secondo. Il terzo e quarto argomento individuano gli estremi dell'intervallo in cui varia la variabile e il quinto si riferisce al passo.

length([x_1,...,x_n])

Fornisce il numero di elementi di una lista. Se applicato ad una matrice ne indica invece il numero di righe.

wxplot2d([discrete,x,y])

Questo comando consente la graficazione discreta, ovvero di tracciare un grafico punto per punto anziché tramite una lista di funzioni. Il comando discrete è seguito da una lista con le coordinate x e una con le coordinate y.

trigsimp

Per considerare le proprietà di base delle funzioni trigonometriche nella valutazione dell'espressione e quindi semplificarla.

expand
trigexpand

Il comando expand e trigexpand riducono rispettivamente un'espressione a somma di monomi e semplificano espressioni trigonometriche come sin(2x), ecc. Il comando trigexpandtimes controlla la regola del prodotto di trigexpand, ovvero quando è impostato su true l'espansione dei prodotti avverrà fino al raggiungimento dei minimi termini scomponibili.

realpart(y)
imagpart(y)

Sia y un numero complesso, tali comandi forniscono la sua parte reale ed immaginaria.

exponentialize(y)

Per passare dalla forma trigonometrica a quella esponenziale del numero complesso.

demoivre(y)

Per passare dalla forma esponenziale complessa a quella trigonometrica.

block([v_1,...,v_m],espres_1,...,espres_n)

Garantisce la non modifica di variabili utilizzate in precedenza racchiudendo il codice che le impiega in un blocco, in questo modo variabili omonime ma con differente contenuto non interferiscono. Il parametro tra parentesi quadra viene utilizzato solo all'interno di questa riga di codice e alla sua fine torna ad assumere il valore precedentemente assegnato. Per scambiare il contenuto di due variabili può risulare utile la definizione di una variabile temporanea tmp.

quad_qag(f(x),x,a,b,metodo)

Consente l'integrazione di una generica funzione su un intervallo finito. In particolare esegue quadrature numeriche con criterio adattivo, raffinando l'intervallo finché non viene raggiunto un certo livello di stima dell'errore. Come input deve essere fornita la funzione da integrare, la variabile di integrazione, gli estremi di integrazione e il metodo di integrazione (la designazione del metodo consiste in un numero intero compreso tra 1 e 6). Come output il comando fornisce: il risultato, l'errore assoluto commesso, il numero di step effettuati e un codice di errore.

Per generare una matrice su Maxima si può procedere in diversi modi:

1. Si inizializza una matrice nulla e poi si sostituiscono i valori nulli con quelli desiderati
2. Si definisce la matrice tramite liste, che ne rappresentano le righe
3. Per definire una matrice i cui elementi sono funzione degli indici di riga e di colonna si impiega il comando genmatrix. Per passare la funzione a genmatrix occorre utilizzare la funzione senza nome lamba, i cui argomenti sono: la lista degli argomenti della funzione e la funzione stessa.

Alcuni esempi:

transpose(A)

Fornisce la trasposta della matrice A.

determinant(A)

Calcola il determinante della matrice A.

augcoefmatrix([eqn_1,...,eqn_m],[x_1,...,x_n])

Fornendo come input un sistema lineare di equazioni e le sue variabili indipendenti, restituisce la matrice dei coefficienti e il termine noto. Altrimenti per ottenere solamente la matrice dei coefficienti si utilizza coefmatrix.

submatrix

Per estrarre la sottomatrice di B

Il metodo di Quadratura Gaussiana permette la risoluzione numerica di integrali di funzioni non risolvibili analiticamente.
Data una generica funzione f(x) si considera un certo numero di punti x _i in cui la funzione viene campionata. A tali valori della funzione f(x _i) viene attribuito un peso w _i. La somma dei pesi è sempre 2. Il risultato dell'integrazione si ottiene come sommatoria negli n punti di campionamento del prodotto fra w _i e f(x _i).
$$ G = \sum_{i=1}^n w_i f(x_i) $$
I punti di campionamento x _i e i pesi w _i vengono calcolati in modo tale che il residuo R, definito come la differenza fra il valore esatto dell'integrale della funzione e il valore calcolato mediante integrazione Gaussiana, risulti funzione dei soli parametri x _i e w _i.

Prendiamo in esame un generico polinomio di terzo grado e procediamo con un metodo di quadratura per due punti.

Indico con x _i1 e x _i2 i punti di campionamento e con w ₁ e w ₂ i rispettivi pesi

Per ricavare le incognite x ₁, x ₂, w ₁, w ₂ devo impostare un sistema di equazioni NON lineari con le quali impongo che il residuo non dipenda dai coefficienti a,b,c,d del polinomio. In altri termini pongo nulle le derivate del residuo fatte rispetto a ciascuno dei coefficienti del polinomio.

In questo modo ottengo un sistema di quattro equazioni in quattro incognite che vado a risolvere utilizzando il comando “solve”

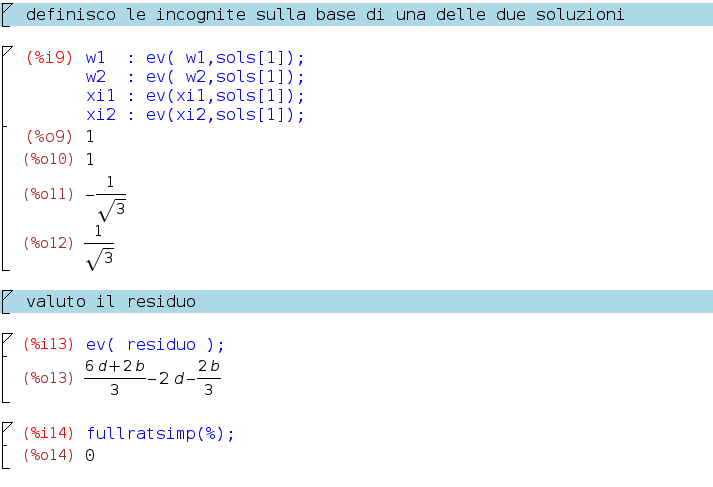
Il sistema ammette due soluzioni, sols[1] e sols[2]. Definisco le incognite sulla base di una delle due soluzioni per mezzo del comando “ev” quindi controllo che tali coefficienti rendano il residuo costante in a,b,c,d. Lo stesso risultato si ottiene valutando il residuo sotto le ipotesi date dalla seconda soluzione del sistema.

Il residuo non dipende dai coefficienti a,b,c,d del polinomio e, in particolare, risulta nullo quindi è stato ottenuto il grado massimo di precisione.
Il metodo di quadratura Gaussiana per un numero n di punti di campionamento, infatti, consente l'integrazione esatta di un polinomio fino al grado 2n+1.

Vediamo il metodo di Gauss utilizzando una funzione diversa dal polinomio, per esempio $\sin(x)$ e la integriamo tra 0 e $\pi$ : $$\int_{0}^{\pi }\sin (x)$$ Occorre effettuare un cambio di variabili: $x(\xi )$ tale che $$\begin{cases} & \text{ } x(-1)=0 \\ & \text{ } x(1)=\pi \end{cases}$$, quindi utilizziamo il polinomio $x(\xi)=a\xi+b$

Il differenziale dx diventa $dx=\frac{d(x(\xi ))}{d\xi }$

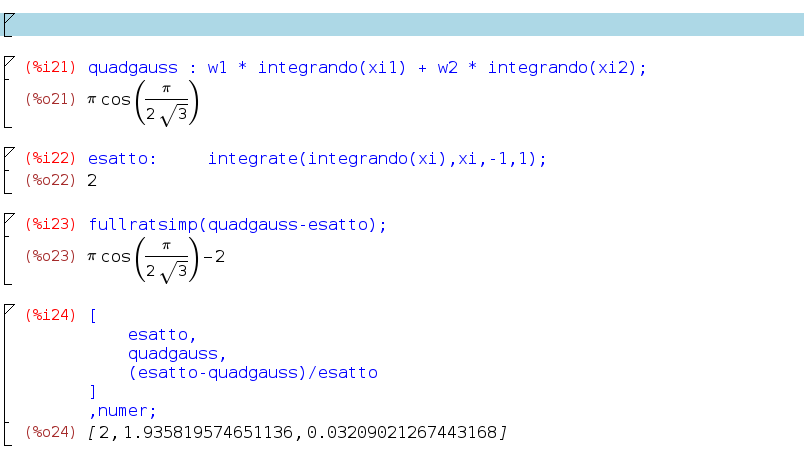
Si ottiene $$\int_{-1}^{1}\sin (x(\xi ))\frac{dx(\xi )}{d\xi }d\xi$$ al quale si applica il metodo di Gauss

Il primo numero tra le parentesi quadre rappresenta il valore esatto, il secondo il residuo e il terzo l'errore relativo.

comandi sparsi maxima

comandi sparsi maxima, a fine lezione

quadratura gaussiana