gdl. nodali: spostamento assiale $w$, spostamento radiale $u$, spostamento circonferenziale $v$ identicamente nullo. coordinate: assiale $a$ e radiale $r$, in MSC.Marc coincidenti con $x$ e $y$ ($x$ è l'asse di assialsimmetria supposto del sistema)

base elemento isoparametrico 4 nodi, def. piana; deformazioni

$$\epsilon_r = \frac{\partial u}{\partial r}$$

$$\epsilon_a = \frac{\partial w}{\partial a}$$

$$\gamma_{ra} = \frac{\partial u}{\partial a}+\frac{\partial w}{\partial r}$$

entro piano radiale-assiale come da elemento in deformazione piana.

Deformazione circonferenziale

$$ \epsilon_{\theta} = \frac{u}{r} $$

Matrice B di legame deformazione

$$ \begin{bmatrix} \epsilon_z\\ \epsilon_r\\ \gamma_{zr}\\ \epsilon_{\theta} \end{bmatrix} = \underbrace{ \begin{bmatrix} \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ \frac{N_1\left(\xi,\eta \right )}{r\left(\xi,\eta \right )}& 0 & \frac{N_2\left(\xi,\eta \right )}{r\left(\xi,\eta \right )}& 0 & \frac{N_3\left(\xi,\eta \right )}{r\left(\xi,\eta \right )}& 0 & \frac{N_4\left(\xi,\eta \right )}{r\left(\xi,\eta \right )}& 0 & \end{bmatrix} }_{\underline{\underline{B}}} \begin{bmatrix} w_1\\ u_1\\ w_2\\ u_2\\ w_3\\ u_3\\ w_4\\ u_4 \end{bmatrix} $$

i termini $\cdot$ sono presi dalla matrice B dell'elemento in deformazione piana, mentre $r(\xi,\eta )=N_1(\xi,\eta ) r_1 +N_2(\xi,\eta ) r_2 + N_3(\xi,\eta ) r_3 +N_4(\xi,\eta ) r_4$

Matrice di legame elastico

$$ \begin{bmatrix} \sigma_z\\ \sigma_r\\ \tau_{zr}\\ \sigma_{\theta} \end{bmatrix} = \frac{E}{(1+\nu)(1-2 \nu)} \begin{bmatrix} 1-\nu & \nu & 0 & \nu\\ \nu & 1-\nu & 0 & \nu\\ 0 & 0 & (1-2\nu)/2 & 0\\ \nu &\nu & 0 & 1-\nu \end{bmatrix} \begin{bmatrix} \epsilon_z\\ \epsilon_r\\ \gamma_{zr}\\ \epsilon_{\theta} \end{bmatrix} $$

Continuiamo la lezione precedente al Marc sul tubo elastoplastico partendo dal file: tubo_ep_v000_06_05_2016.mud Eravamo arrivati a definire una mesh,una proprietà geometrica e una proprietà del materiale; il materiale era elastoplatico. Andiamo a MATERIAL PROPERTIES –> MATERIAL PROPERTIES –> STRUCTURAL in Data Categories –> PLASTICITY PROPERTIES e andiamo a controllare che il Yield Stress sia 400

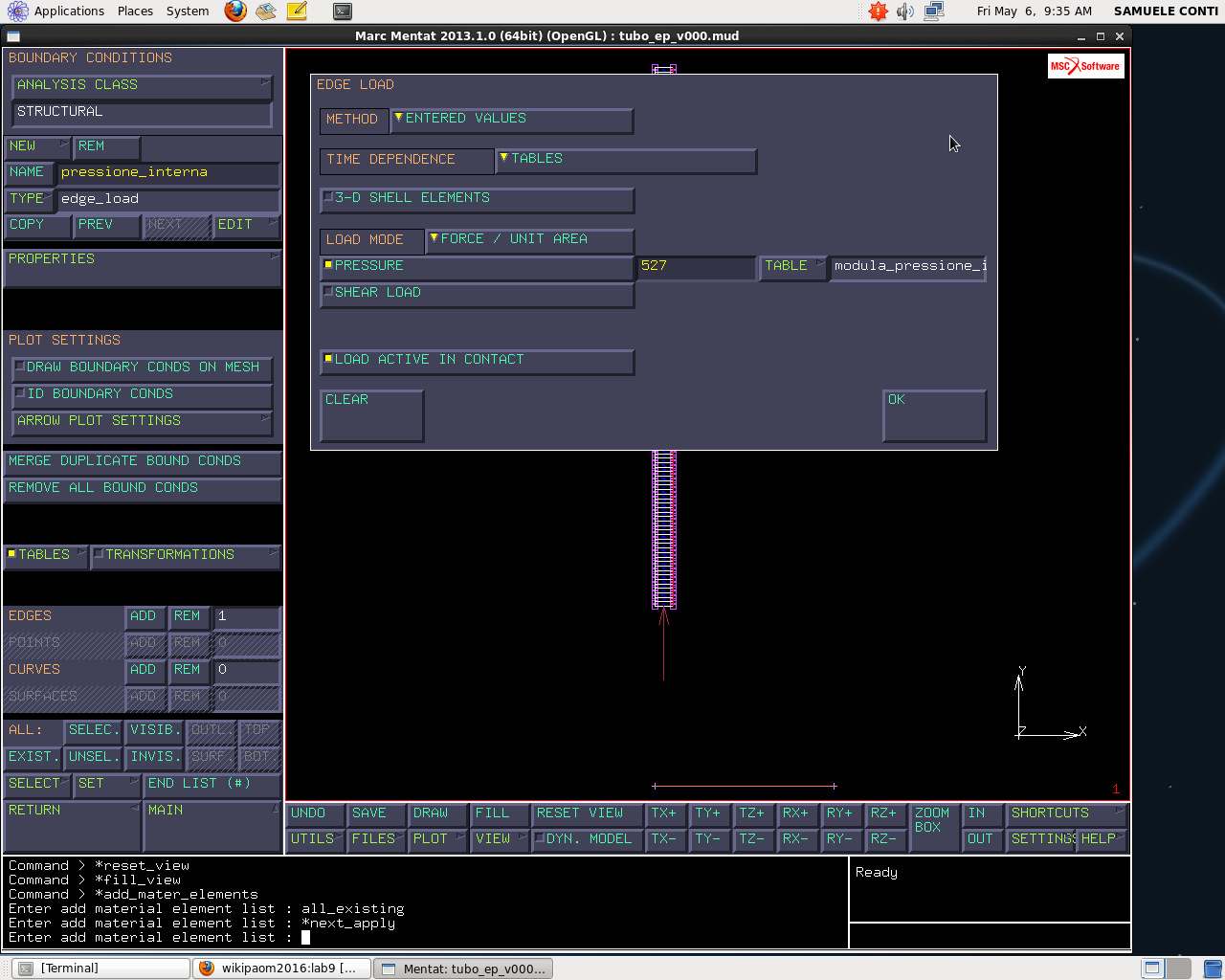
Associamo questa proprietà a tutti gli elementi del materiale tramite ELEMENTS ADD –> SELECT –>ALL. Andiamo a verificare i servolink che abbiamo creato la scorsa volta e la pressione interna:

Abbiamo imposto una pressione interna che ha un valore non fisso massimo di 527 MPa, ossia modula secondo questa tabella modulo a flessione. Andiamo a MATERIAL PROPERTIES –> MATERIAL PROPERTIES –> TABLES –>FIT :

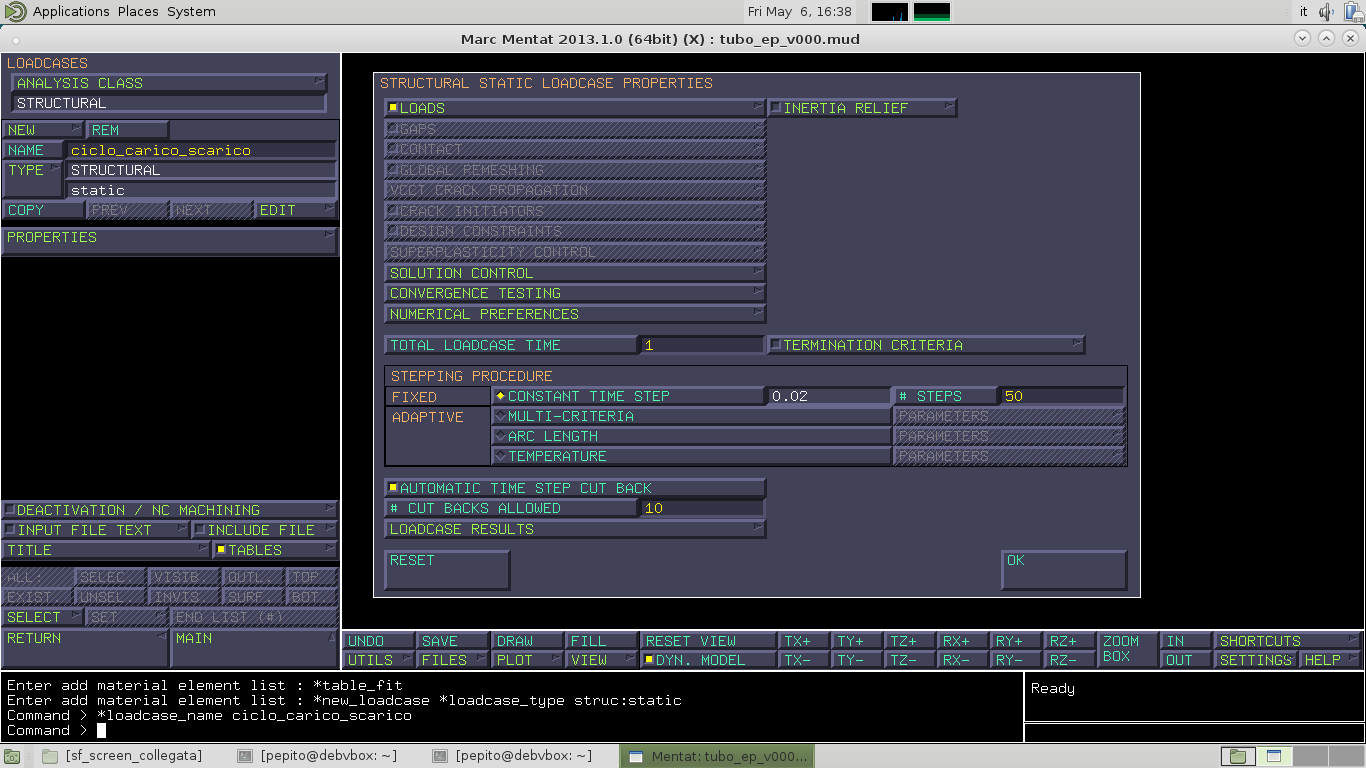
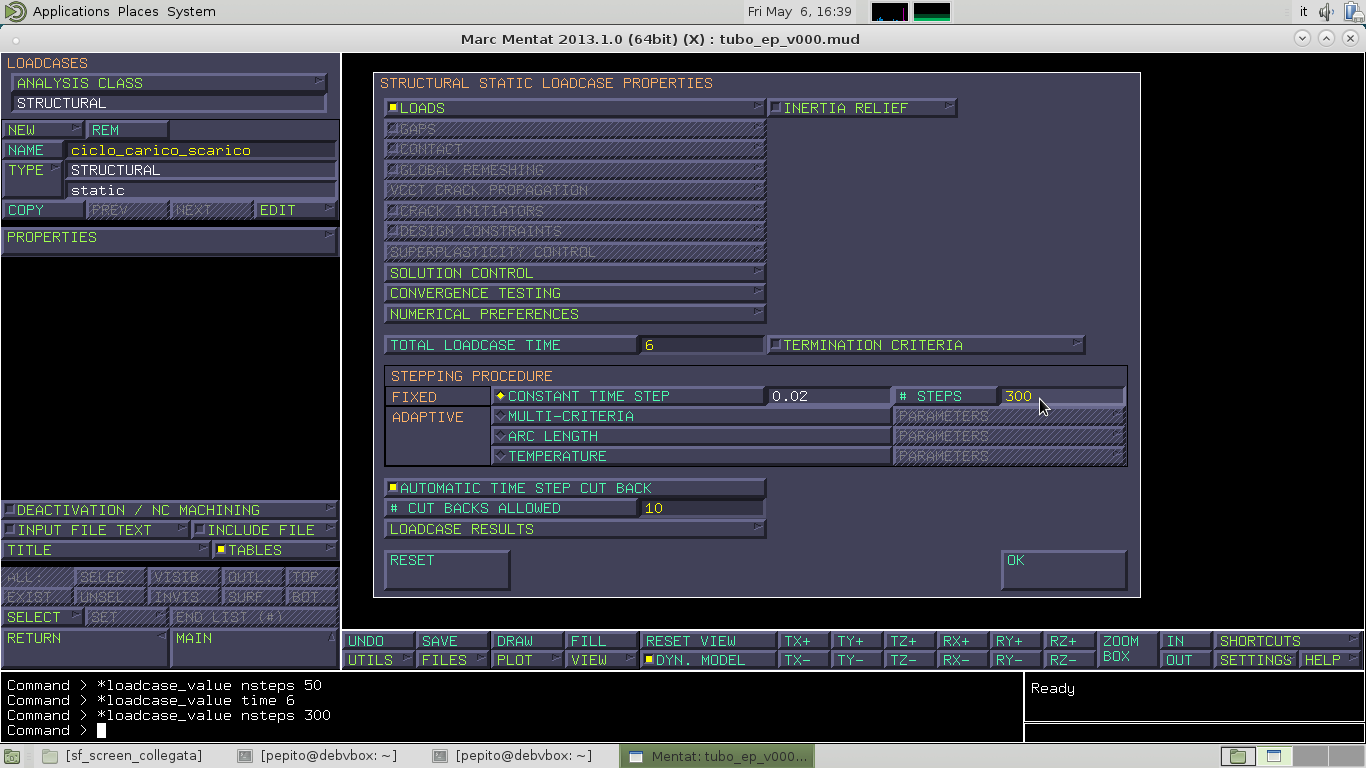
Andiamo a definire un pezzo della storia di carico dal MAIN–>LOADCASES. Creiamo un nuovo LoadCases e lo chiamo ciclo_carico_scarico –>NEW–>STATIC–>PROPERTIES.

TOTAL LOADCASE TIME rappresenta la durata della storia di carico e scarico. Nella figura precedente era impostato un TOTAL LOADCASE TIME unitario che corrispondeva alla prima fase di carico diviso in 50 step. Andiamo ora a considerare 3 cicli di carico e scarico impostando in TOTAL LOADCASE TIME il valore 6 e sostituendo in # STEPS il valore di 300.

Entrando in LOADS troviamo le boundary condition attive nella storia di carico, lasciandole entrambe attive:

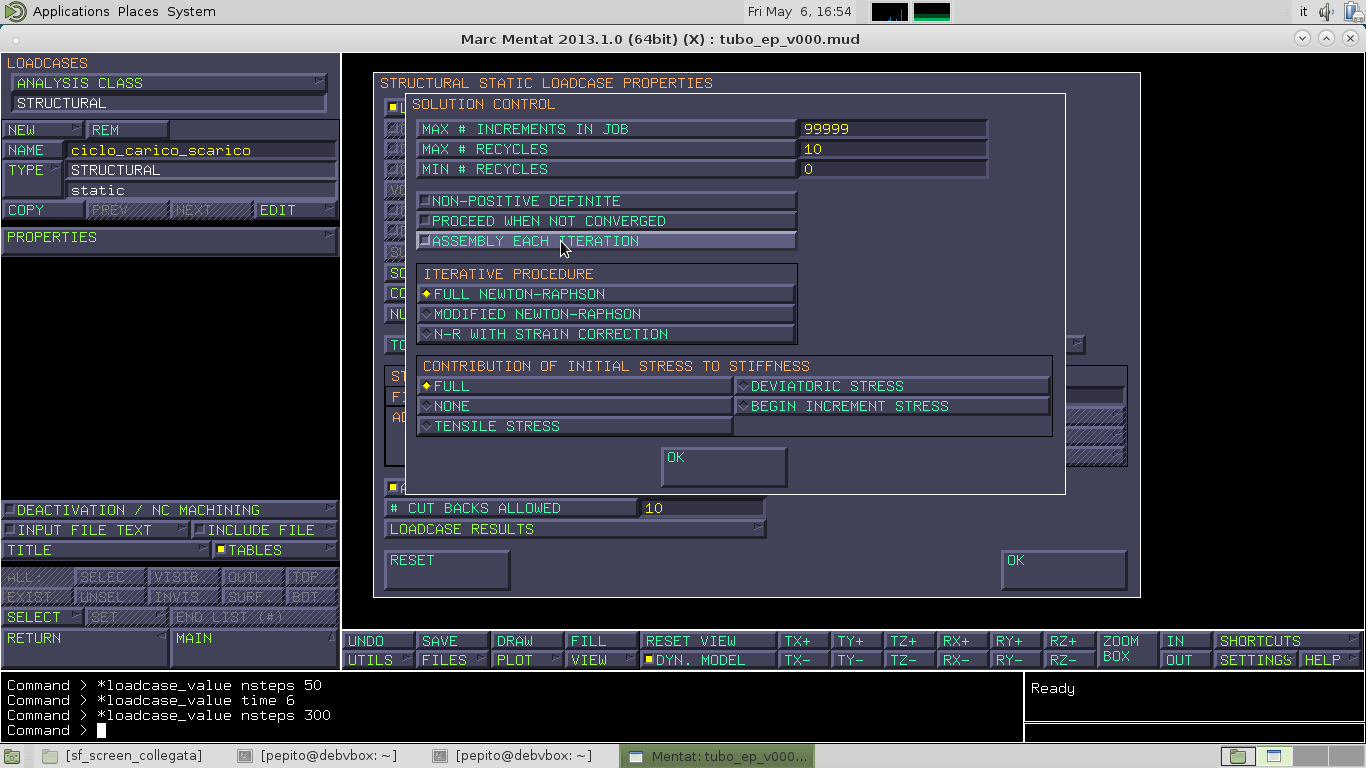
Entrando in SOLUTION CONTROL imponiamo che il metodo Newton-Raphson possa fare massimo 10 iterazioni.

Andiamo in CONVERGENCE TESTING dove RELATIVE FORCE TOLERANCE posta a 0.1 ci dice che la tolleranza è un decimo di un valore di un valore di riferimento, ossia la più alta reazione vincolare nel modello

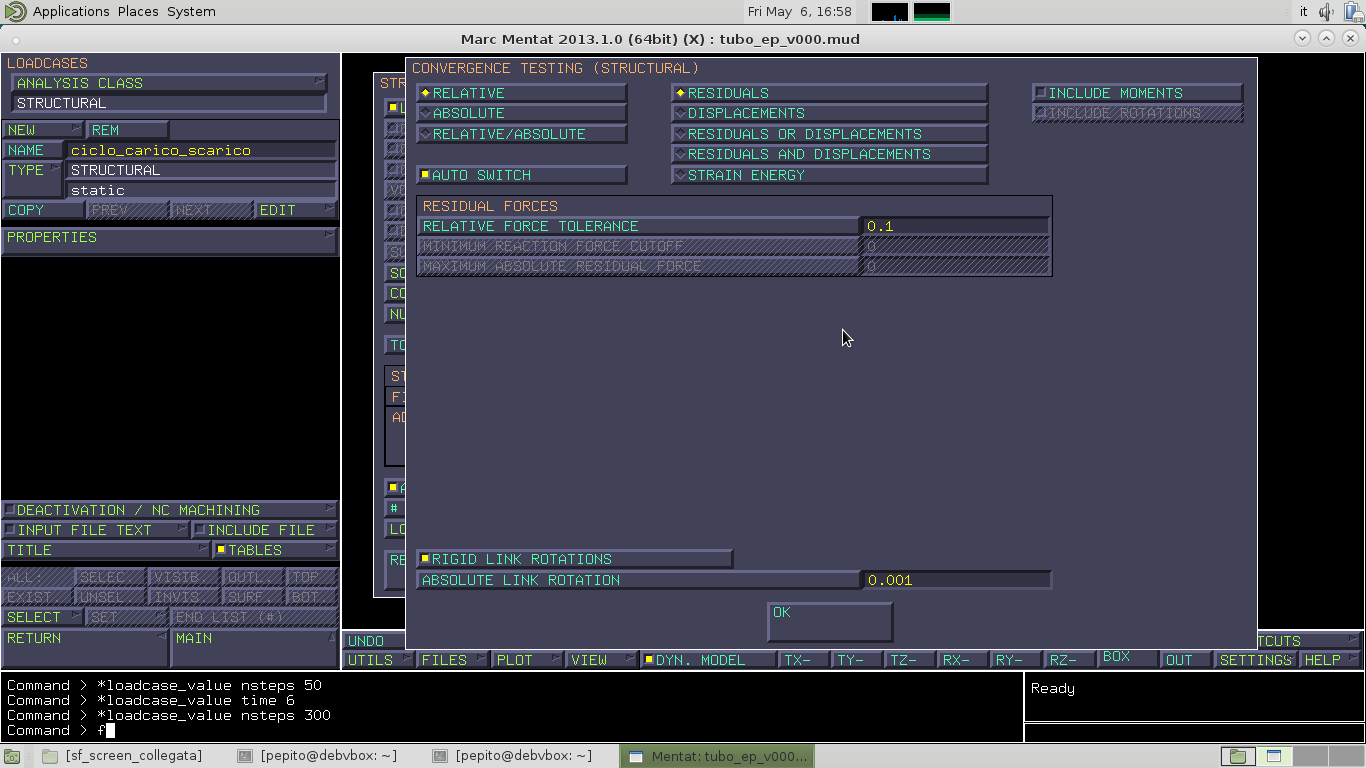
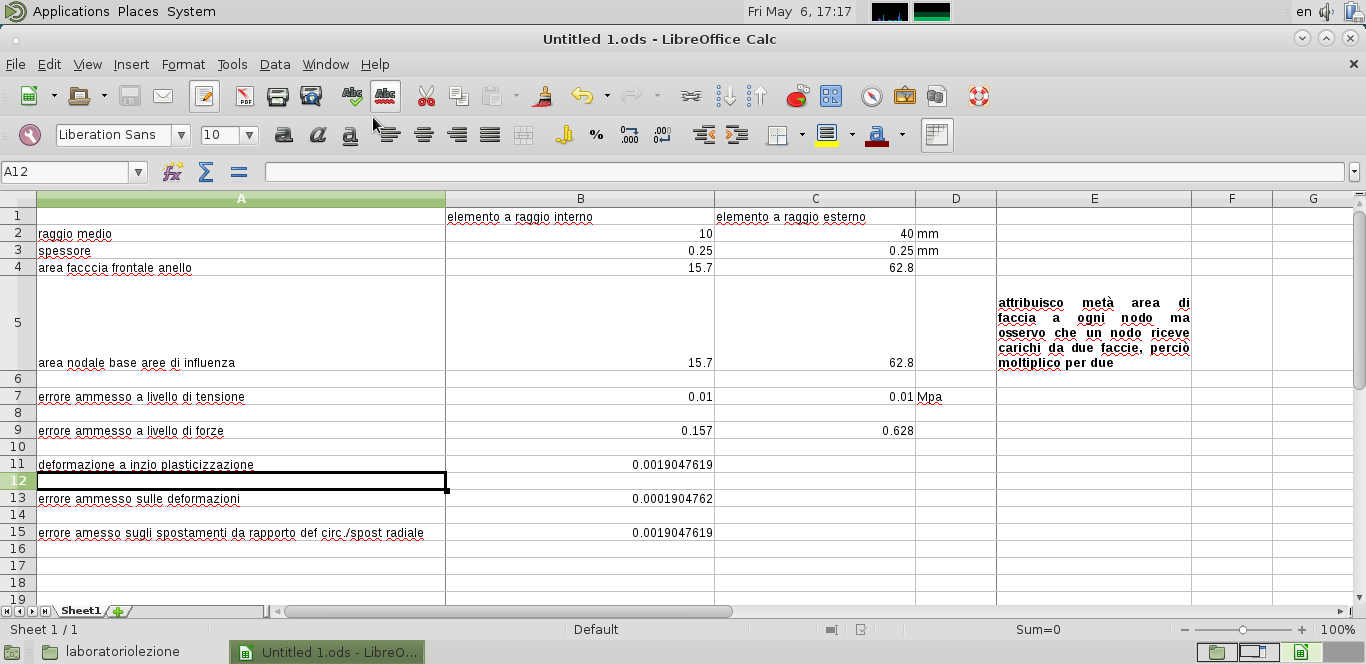
Facendo riferimento al seguente foglio di calcolo andiamo a vedere, imposto l'errore ammesso a livello di tensione, l'errore ammesso a livello di forze e l'errore ammesso sugli spostamenti, dato dal rapporto tra deformazione circonferenziale e spostamento radiale.

Andiamo a impostarlo al Marc e sempre in CONVERGENCE TESTING selezioniamo ABSOLUTE e RESIDUAL AND DISPLACEMENT. In RESIDUAL FORCE –>MAXIMUM ABSOLUTE RESIDUAL FORCE impostiamo il valore 0.15(presente nel foglio excel in valore 0.157) e in DISPLACEMENTS–> MAXIMUM ABSOLUTE DISPLACEMENT il valore di 0.002(presente nel foglio excel in valore 0.0019047619)

Aumentiamo il numero di iterazione per essere sicuri di arrivare a convergenza, andiamo in LOADCASES–>PROPERTIES–>SOLUTION CONTROLS–>MAX # RECYCLES e impostiamo 40.

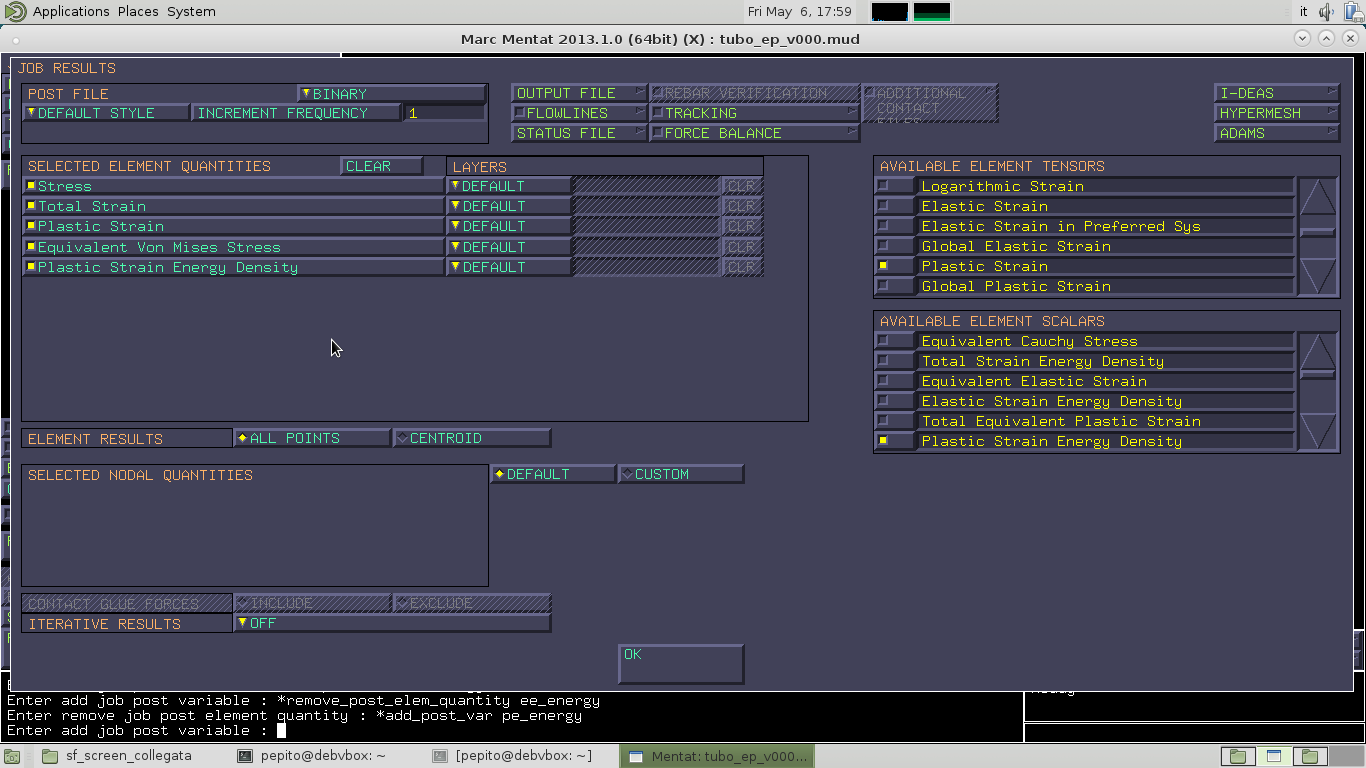
Andiamo ora a fare i calcoli, quindi torniamo al menù principale JOBS –> NEW–>STRUCTURAL–>PROPERTIES–>INITIAL LOAD e deselezioniamo pressione_interna. Sempre in PROPERTIES andiamo in JOB RESULT e selezioniamo da AVAILABLE ELEMENT TENSORS le voci Total Strain,Plastic Strain e Stress, invece da AVAILABLE ELEMENT SCALARS le voci Equivalent Von Mises Stress e Plastic Strain Energy Density.

Ritornando in PROPERTIES attiviamo la storia di carico selezionando ciclo_carico_scarico.

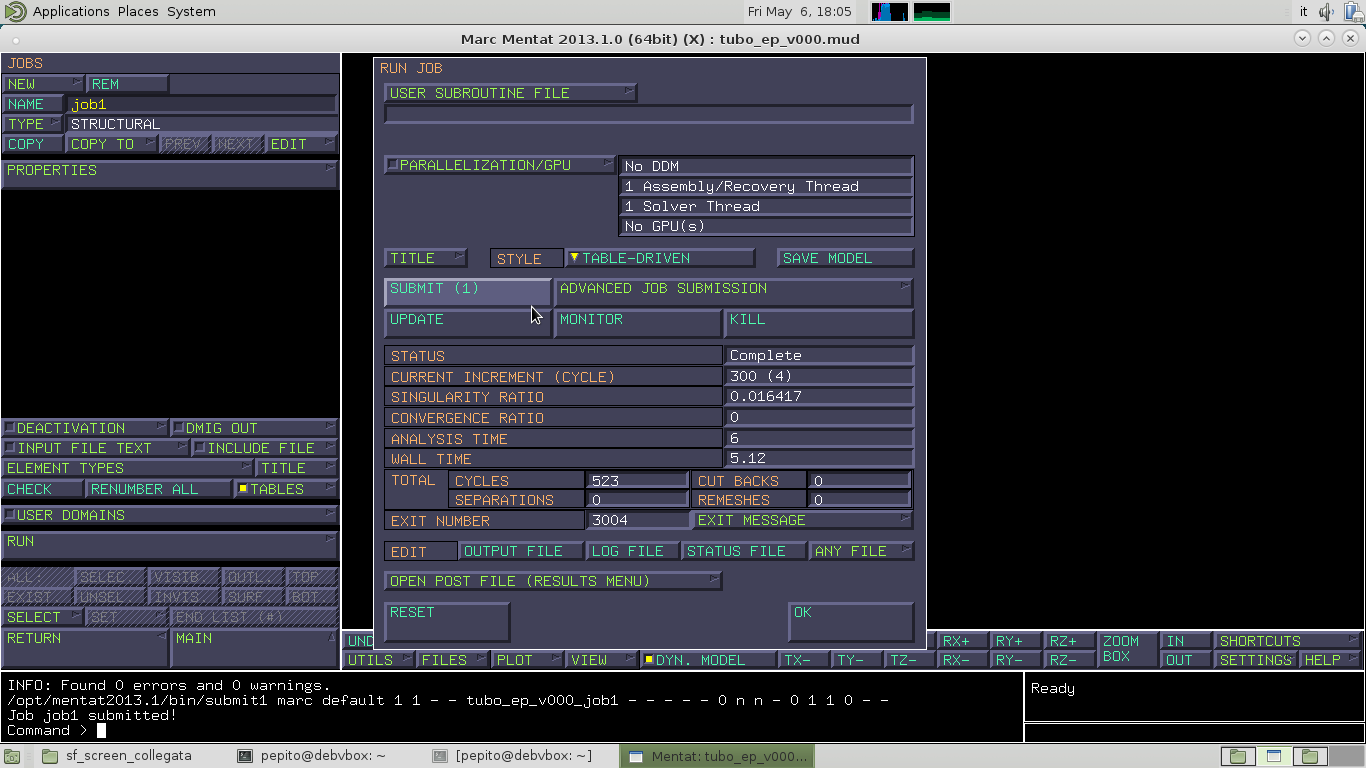
Facciamo partire il calcolo in JOB –>RUN–>SUBMIT(1)

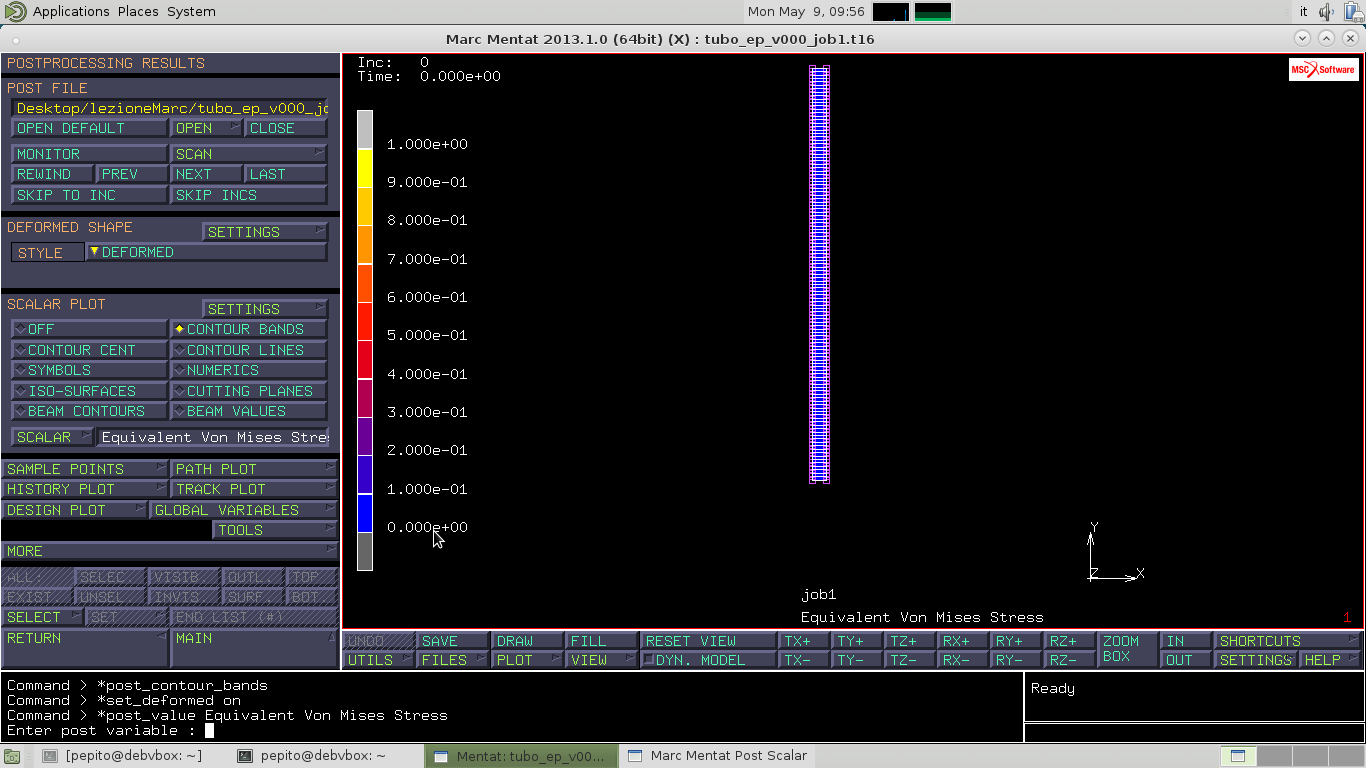
Una volta risolti i calcoli apriamo i risultati OPEN POST FILE. Nel menù SCALAR PLOT apro SCALAR e vado a selezionare Equivalent Von Mises Stress. Seleziono CONTOUR BANDS. Dai risultati abbiamo notato che sono state effettuate in 300 incrementi, visualizzatili in ordine attraverso il tasto NEXT

In SCALAR PLOTS seleziono SETTINGS–>EXTRAPOLATION e selezioniamo in METHOD–>TRANSLATE e in NODAL AVERAGING–>OFF

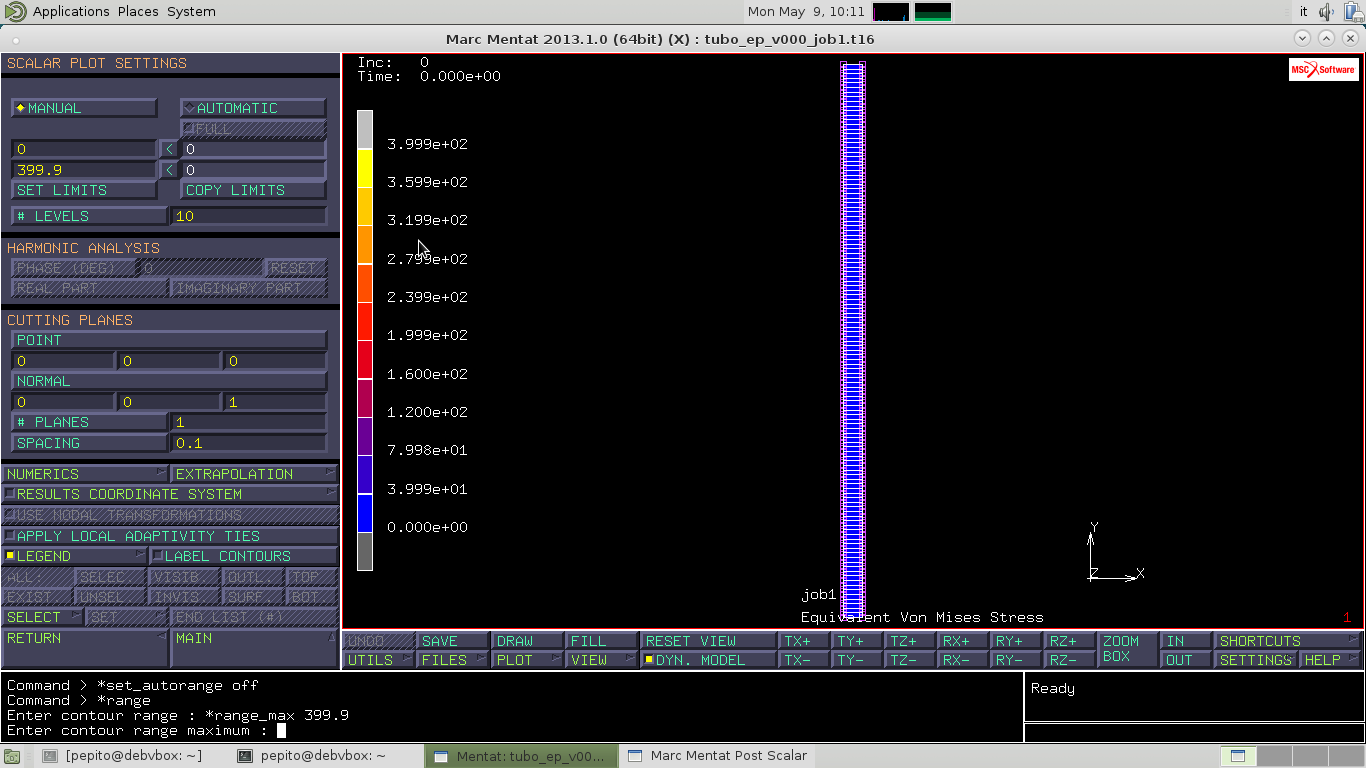
Sempre in SCALAR PLOT SETTINGS selezioniamo MANUAL e impostiamo i valori 0 e 399.9, in maniera tale da far comparire in color grigio i tratti snervati essendo 400 il valore limite.

Facendo in POST PROCESSING RESULT cliccando NEXT e arrivando allo step 50 equivalente all'istante 1s (in quest'istante abbiamo una pressione interna di 527 MPa), si può osservare lo stato tensionale della struttura, la parte grigia indica la parte snervata del materiale.

Possiamo vedere lo snervamento in funzione della deformazione plastica selezionando in SCALAR PLOTS–>SCALAR –>Plastic Strain Energy Density, impostando al SETTING–>MANUAL i valori di 0.0001 e 3.58141.

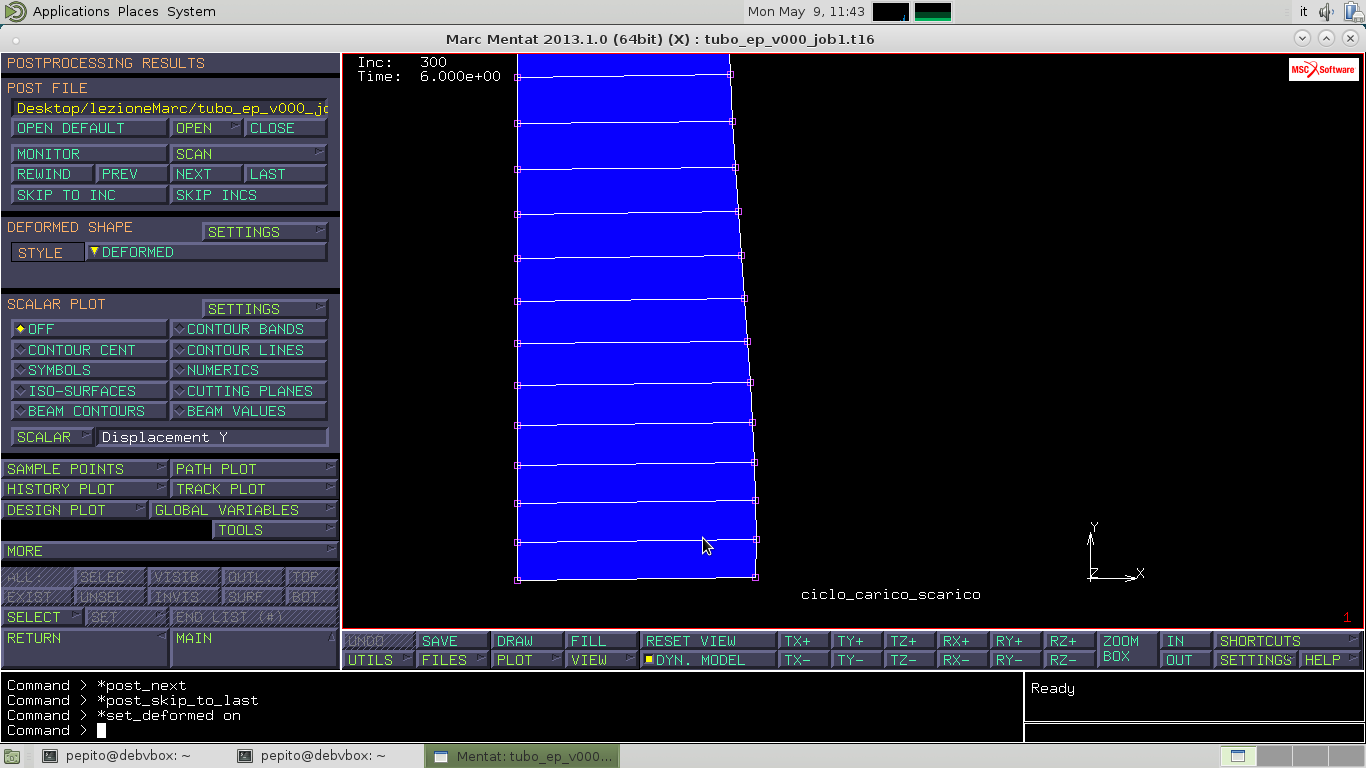
Torniamo adesso a Equivalent Von Mises Stress e andando allo step 51, si nota che non ci sono più tratti grigi; non si osserva più lo snervamento perchè è iniziata la fase di scarico.

Sempre tramite NEXT arriviamo a 100 che corrisponde a 2 secondi. Qui si nota come la figura non sia tutta blu come all'istante zero dato che c'è stato snervamento a compressione.

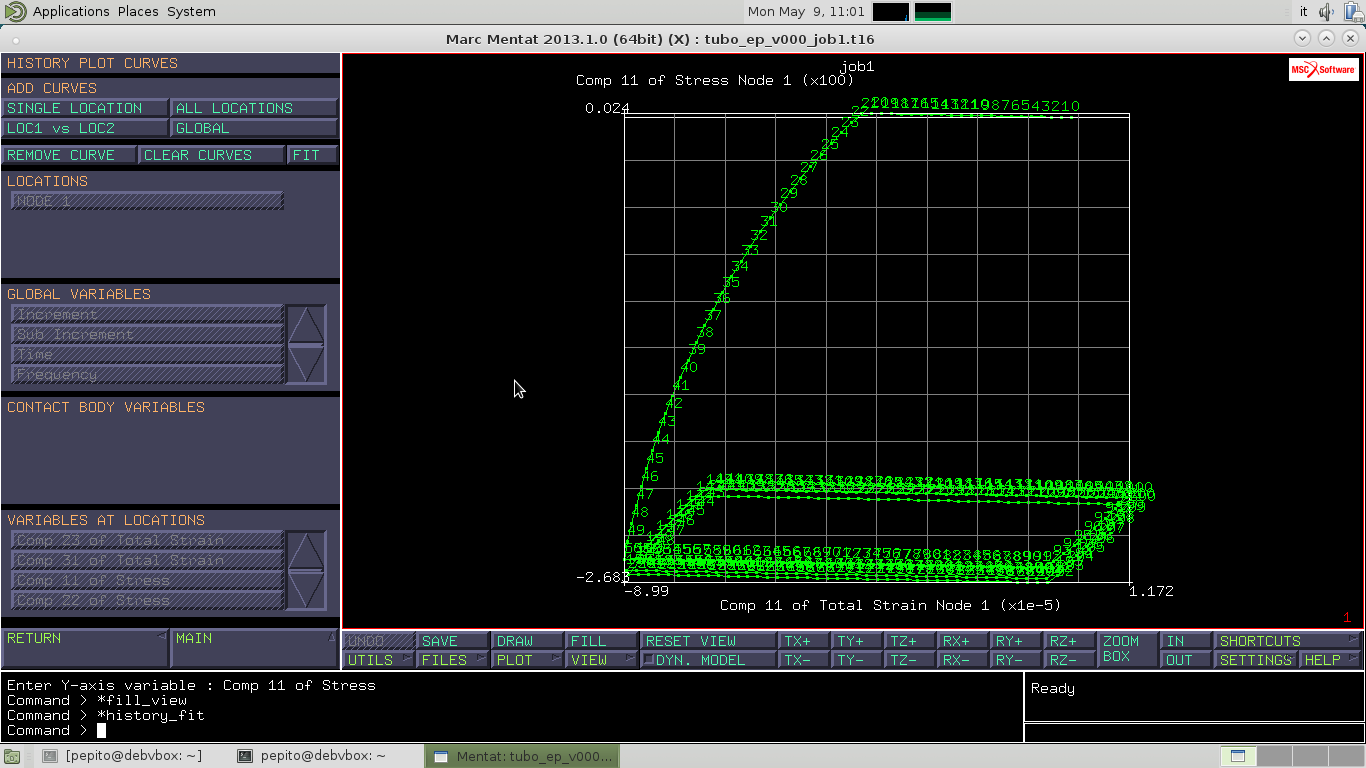
Passiamo alla rappresentazione dei cicli di isteresi tramite i seguenti passaggi. Andiamo in HISTORY PLOT e selezioni SET LOCATION e seleziono il nodo in basso a sinistra. Inoltre seleziono ALL INCS ossia vale per tutti gli step

Seleziono ADD CURVES–>ALL LOCATIONS e vado in VARIABLES AT LOCATIONS e selezioniamo per l'asse x Comp 11 Of Total Strain e per l'asse y Comp 11 Of Stress. Selezione FIT e osservo il grafico.

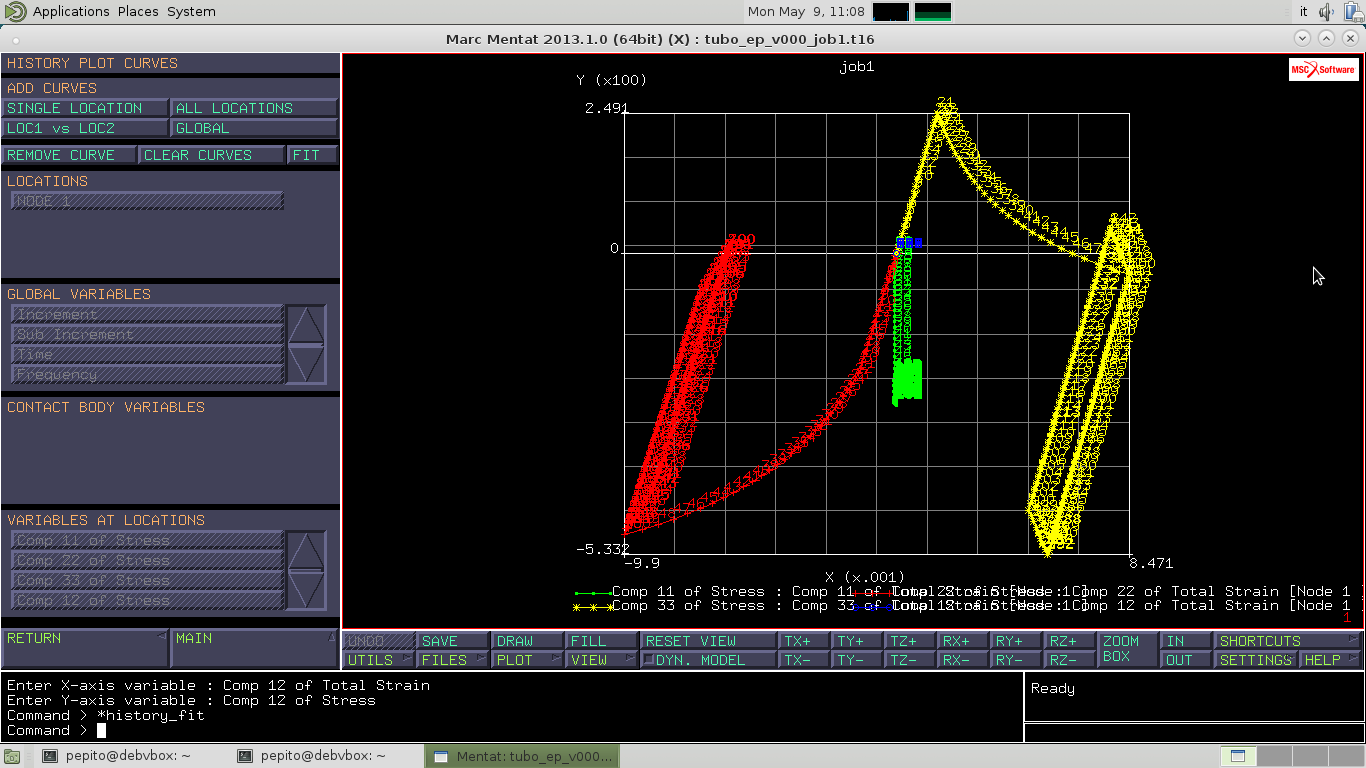
Ripeto gli stessi passaggi per la componente 22 e 33 e 12 e ottengo per ogni componente così un ciclo di isteresi.

In HISTORY PLOTS inserisco in SHOW IDS il valore 10 diminuendo il numero di punti visibili per rendere il grafico più leggibile.

La componente 11 of Stress rappresenta la componente assiale, quella 22 rappresenta quella radiale, la componente 33 quella circonferenziale e quella 12 un taglio in direzione assiale radiale. Nel grafico si può osservare che i tratti lineari rappresentano il caricamento elastico, quelli discendenti lo scaricamento.

In POSTPROCESSING RESULT seleziono CLOSE e seleziono DEFORMED E ORIGINAL. Se non siamo sicuri del valore dell'errore ammesso possiamo procedere così: dal MAIN –>LOADCASES–>PROPERTIES–>CONVERGENCE TESTING e in RESIDUAL FORCES –>MAXIMUM ABSOLUTE RESIDUAL FORCE inserisco il valore di 0.015.

e faccio ripartire il calcolo da JOBS–>RUN–>SUBMIT(1). Si possono rifare i cicli di isteresi e confrontarli con quelli del caso precedente.

Se togliamo i link vediamo come la struttura si deforma; per fare ciò vado in LINKS–>NODAL TIES–>REM. ALL TIES. Faccio ripartire il calcolo da JOBS–>RUN–>SUBMIT(1). Apro i risultati mediante OPEN POST FILE e osservo la deformazione al'ultimo step

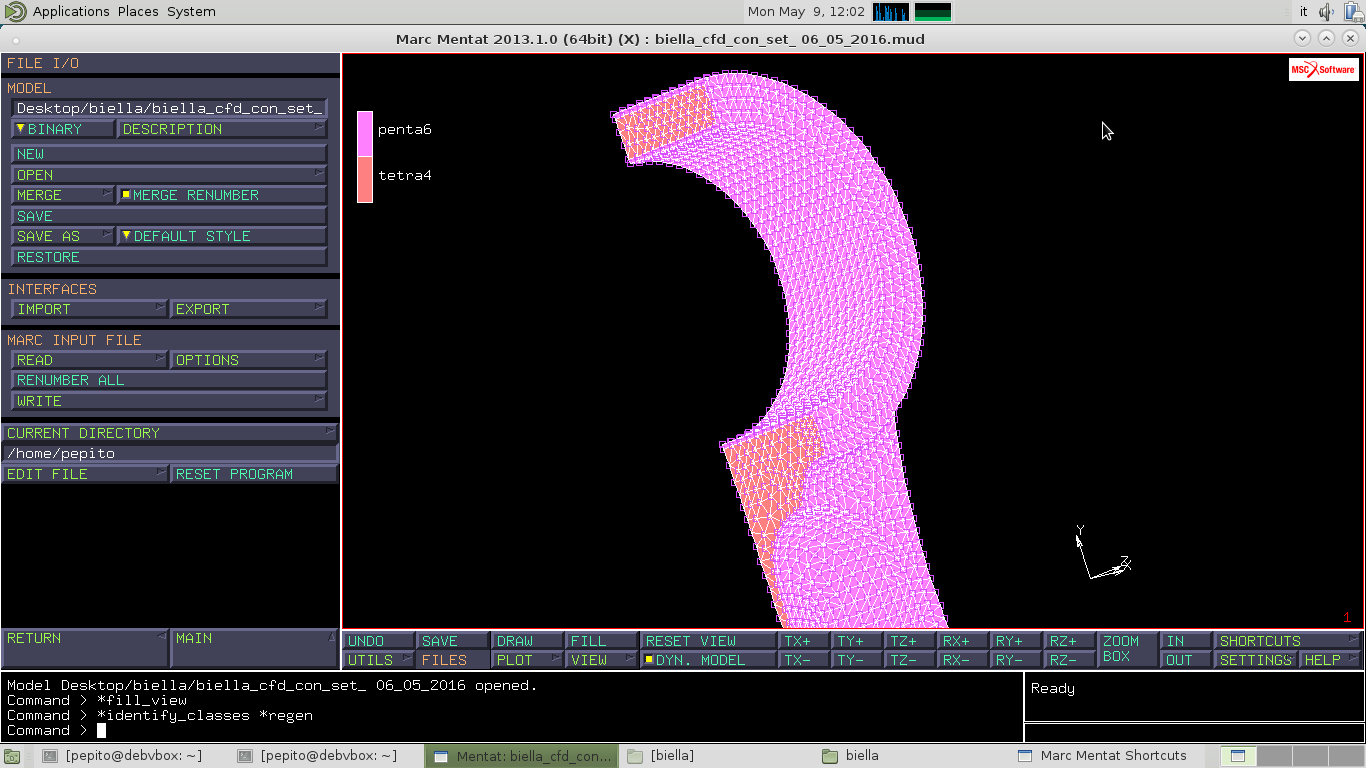
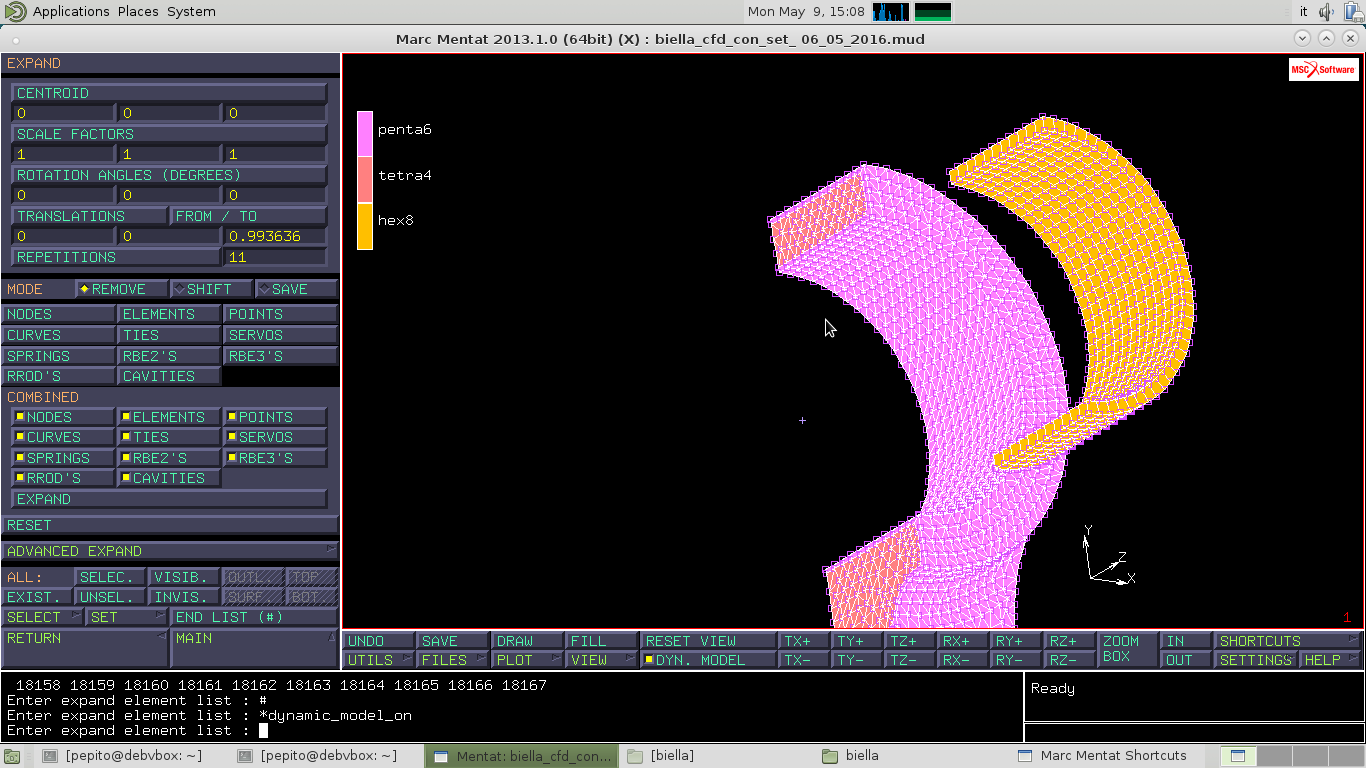
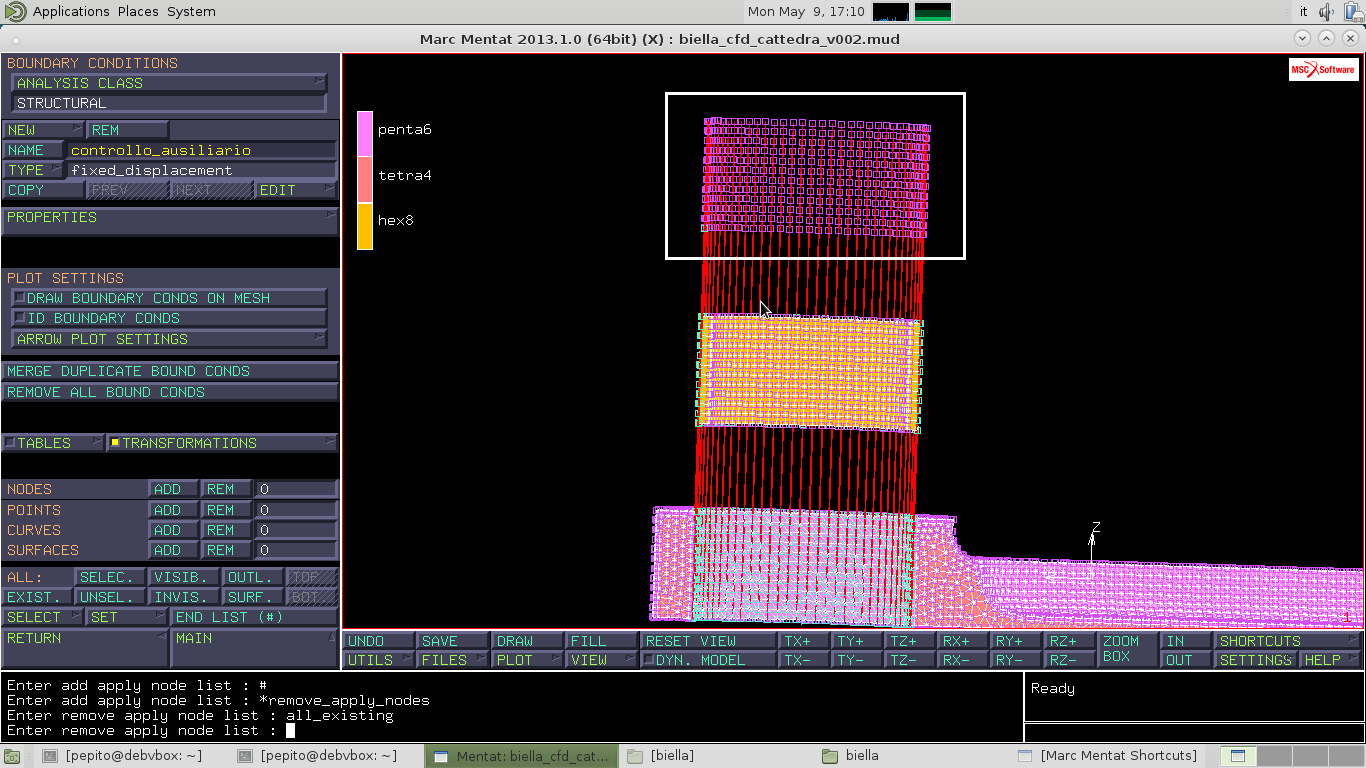
Prendo il file biella_cfd_con_set_06_05_2016.mud Abbiamo 1/4 di piede di biella ed è formato da due diverse tipi di mesh che possiamo vedere tramite SHORTCUTS e seleziono ELEMENTS CLASS con cui riesco a osservare i due differenti tipi di elementi utilizzati per la mesh, per il nucleo elementi tetraedrici TETRA4 e per la parte esterna PENTA6

Faccio in modo che il centro del sistema di riferimento si trovi nel centro della circonferenza della biella, quindi devo fare un cambio di coordinate. Per fare ciò vado in MESH GENERATION–>BETWEEN POINT e selezioni i due punti in figura

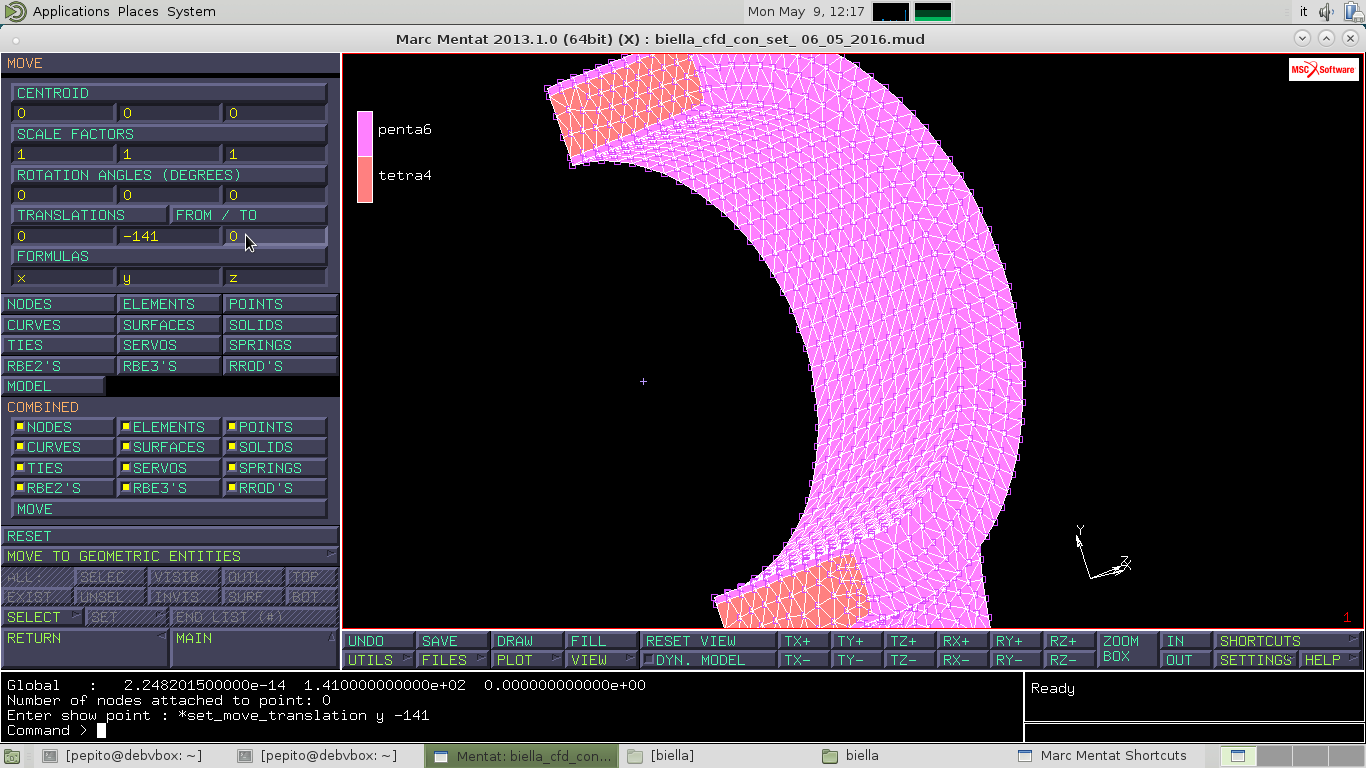
Vediamo le coordinate del punto appena definito tramite PTS–>SHOW, e per spostare il centro del sistema in questo punto seleziono MOVE –> e in TRANSLATION inserisco 0,-141,0 e schiaccio MODEL

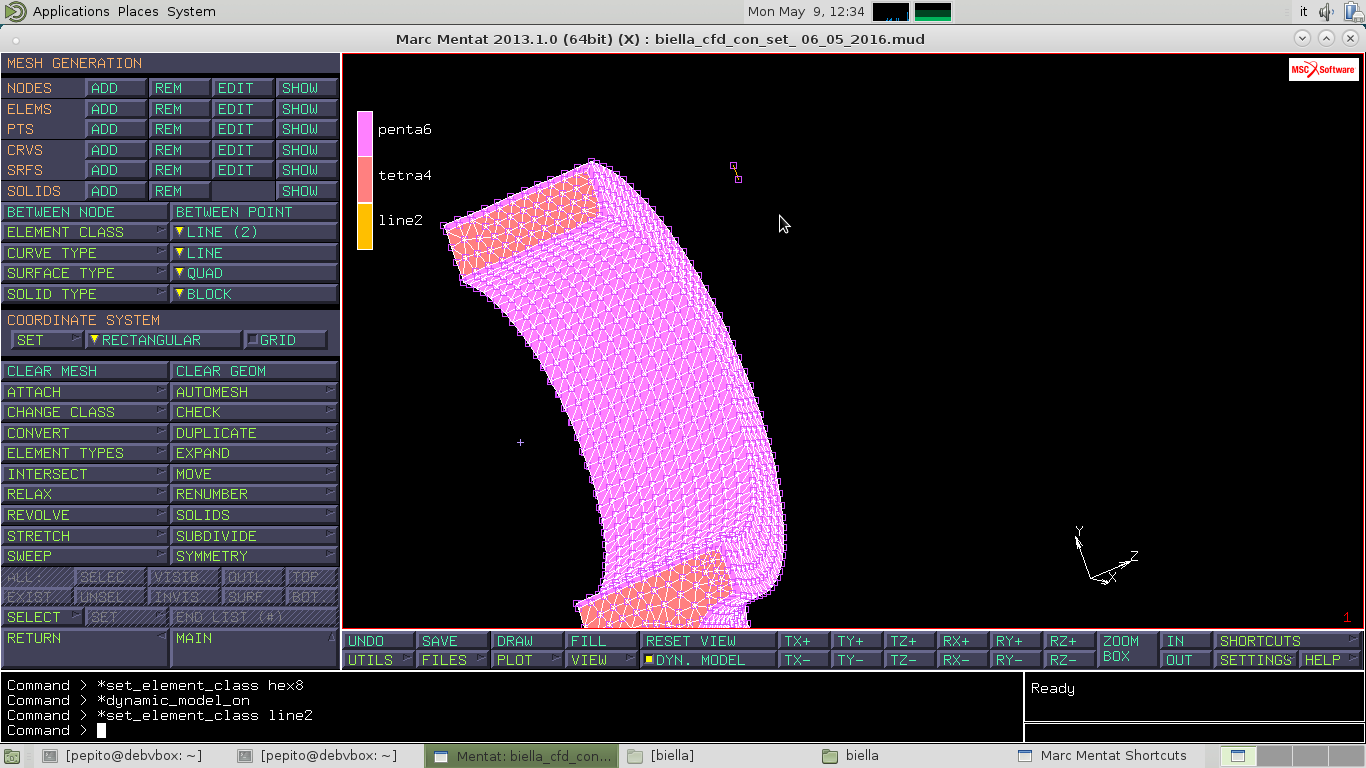
Per creare la bronzina, tubo a parete sottile fatto di acciaio, dove sulla superficie è presente un materiale antifrizione procedo così: MESH GENERATION–>NODES ADD e inserisco le coordinate di 2 nuovi nodi, rispettivamente '0', '22.5/2', '20' e '0','22.5/2-1','20'. Successivamente ELEMENTS ADD e seleziono i due nodi, imposto come ELEMENT CLASS–>LINE(2)

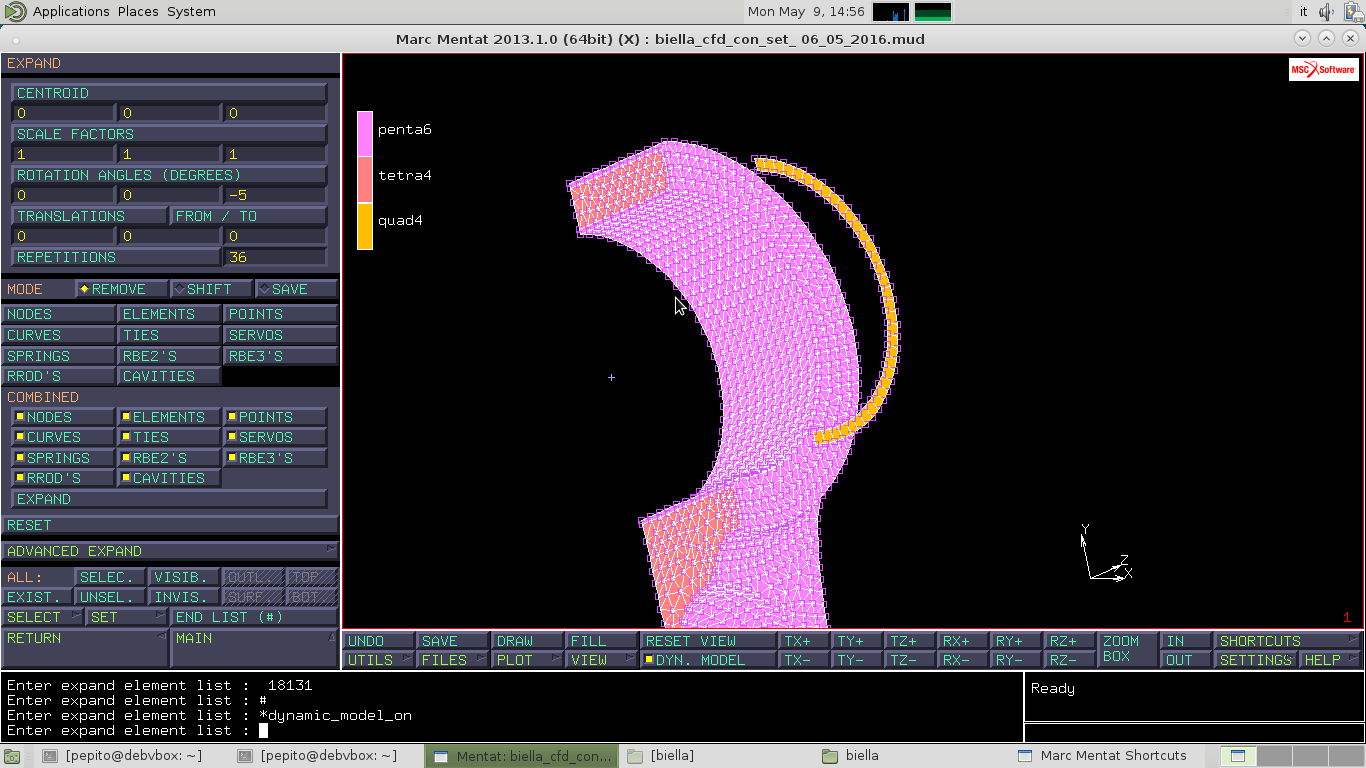
Per estrudere in direzione circonferenziale sempre in MESH GENERATIONvado su EXPAND e inserisco in ROTATION ANGLES i valori '0','0','-5' e in REPETITIONS il valore 36 e conELEMENTS ADD seleziono la linea fatta prima.

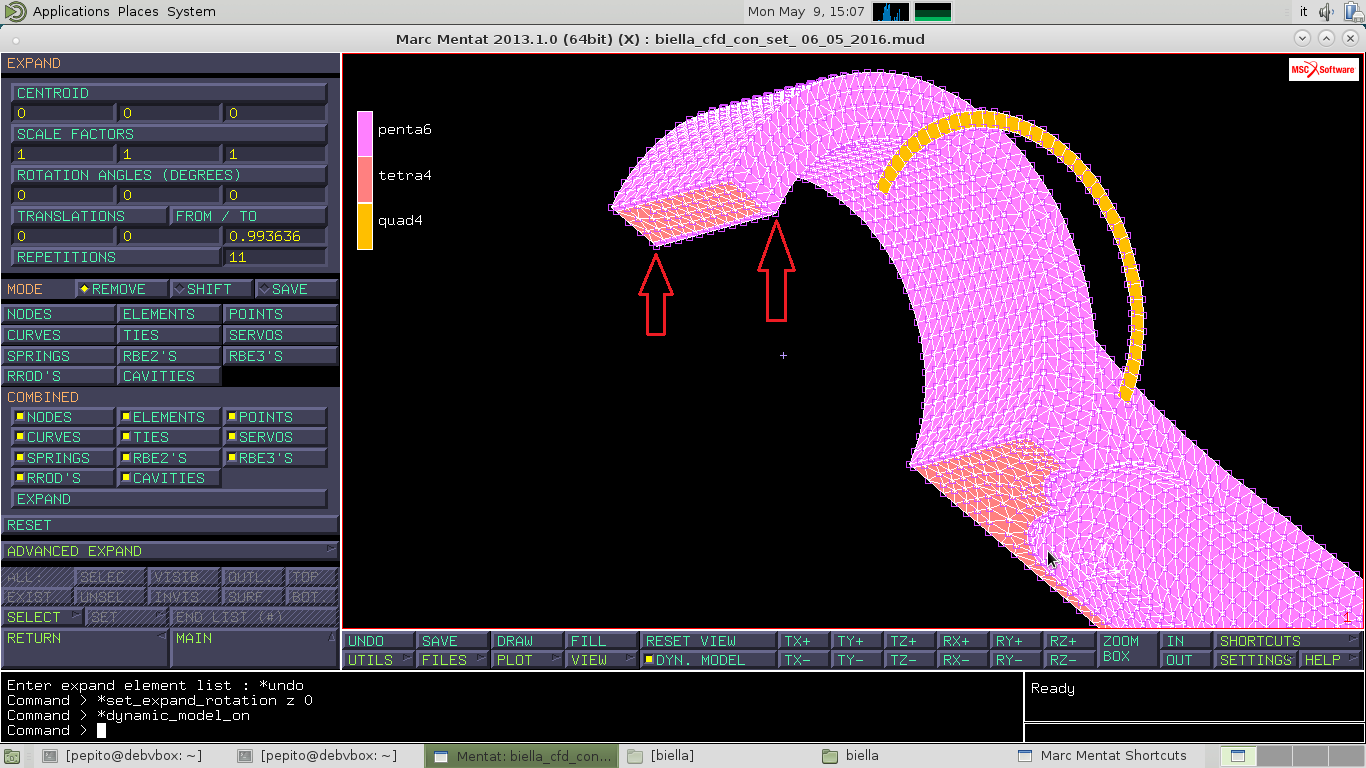
Sempre su EXPAND faccio la seconda estrusione, andando prima a valutare l'altezza dell'estrusione con il comando FROM TO e selezionando i due punti in figura. Vado a cambiare i valori del FROM TO inserendo in direzione x,y il valore 0 e su z dividendo il valore per 11. Inserisco nel REPETITIONS il valore 11.

Premo ELEMENT–>SELECT e seleziono tutta la semicorona della bronzina (in giallo) e faccio lEND LIST.

Consideriamo l'interferenza tra piede e bronzina. Per l'interferenza si va a considerare questo vincolo cinematico: $$ U_{r,p,i}=U_{r,b,i}+\Delta r $$

dove $U_{r,p,i}$ è lo spostamento radiale del nodo i-esimo del piede, $U_{r,b,i}$ è lo spostamento radiale del nodo i-esimo della bronzina, e $\Delta r$ è l'interferenza radiale. Con questo vincolo si va a definire l'interferenza in assenza di attrito. Aggiungendo un altro vincolo a quello precedente ossia: $$U_{\theta ,p,i}=U_{\theta,b,i}$$ avremo interferenza in presenza di attrito e perciò avremo aderenza tra i due pezzi.

Nel nostro caso andiamo a considerare tre nodi, uno sul piede, uno sulla bronzina e un nodo ausiliare($\Delta r$), in formule:

$$U_{r,p,i}=U_{r,b,i}+U_{r,a,i}$$

$$U_{\theta ,p,i}=U_{\theta,b,i}+U_{\theta,a,i}$$

In 3D dobbiamo aggiungere questi due vincoli anche in direzione assiale, ossia nel nostro caso in asse $z$: $$U_{z ,p,i}=U_{z,b,i}+U_{z,a,i}$$ $$U_{\theta ,p,i}=U_{\theta,b,i}+U_{\theta,a,i}$$.

Se impongo gli spostamenti in direzione assiale $z$ sono nulli lavoro con ipotesi di aderenza. Se invece li impongo diversi da zero lavoro con ipotesi di non aderenza

Per imporre questi vincoli nella maniera descritta. Aggiungo il nodo ausiliario tramite MESH GENERATION faccio NODES ADD e inserisco un nodo in coordinate '0','22.5/2','40'. Devo cambiare le coordinate.Vado a MAIN–>BOUNDARY CONDITIONS–>TRANSFORMATION–>COORDINATE SYSTEM–>NEW–>CYLINDRICAL e lascio la configurazione di default

Torno tramite RETURN a TRASFORMATION–>NEW e in COORDINATE SYSTEM seleziono la voce del sistema definito. Faccio NODES ADD–>SELECTe seleziono tramite il tasto 'ctrl' i nodi come in figura sotto:

Sempre in TRASFORMATION vado in TRASFORMATION PLOT SETTINGS–>TRASFORMATIONS e lascio tutte le voci selezionate e poi REGEN.

Nel caso in cui avessi selezionato erroneamente nodi, vado in SELECT–>SELECT BY–>NODES BY–>TRASFORMATION e selezionare la voce della trasformazioni in maniera tale da rendere visibili i nodi selezionati precedentemente;

posso eliminarli manualmente tramite NODES–>REM.

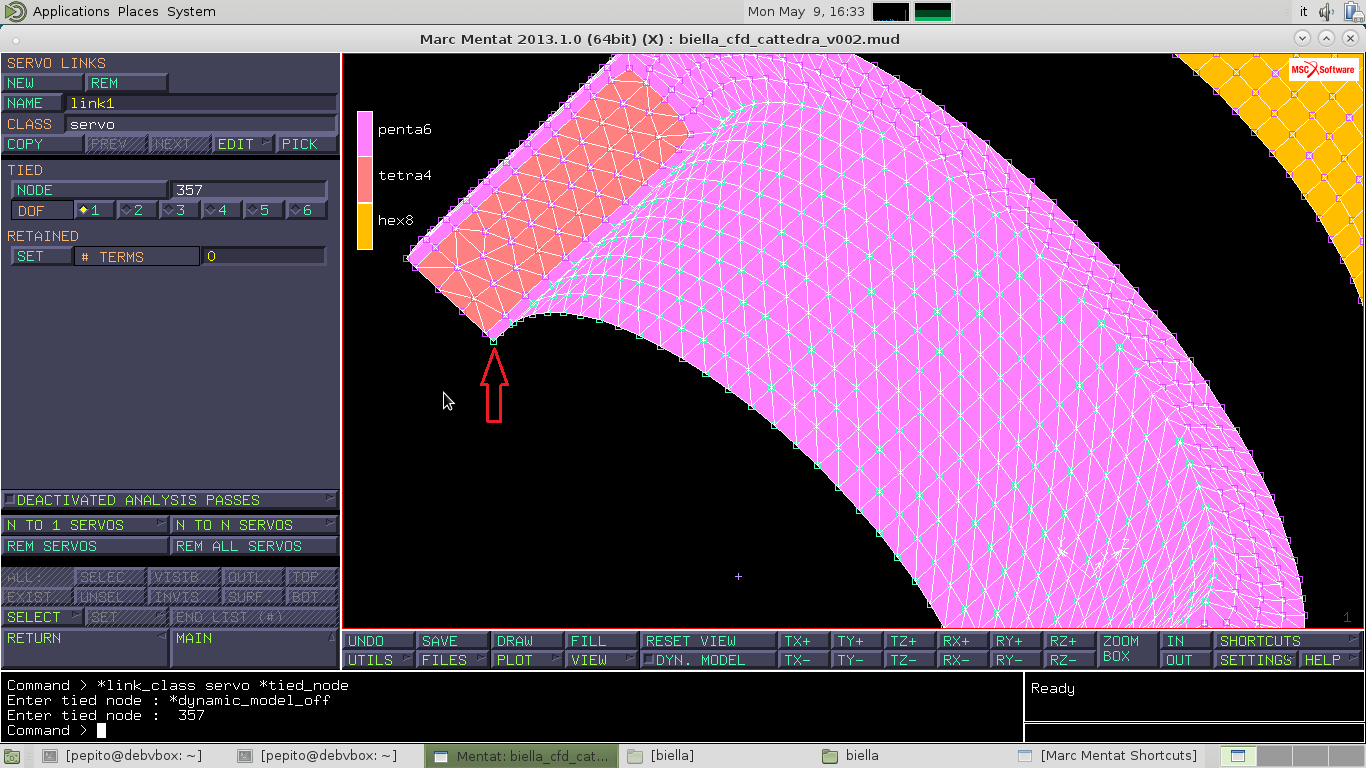
Torno al MAIN e vado in LINKS–>SERVO LINKS–>NEW In TIED–>DOF seleziono il valore '1'. Premo NODE e seleziono il nodo della biella come in figura.

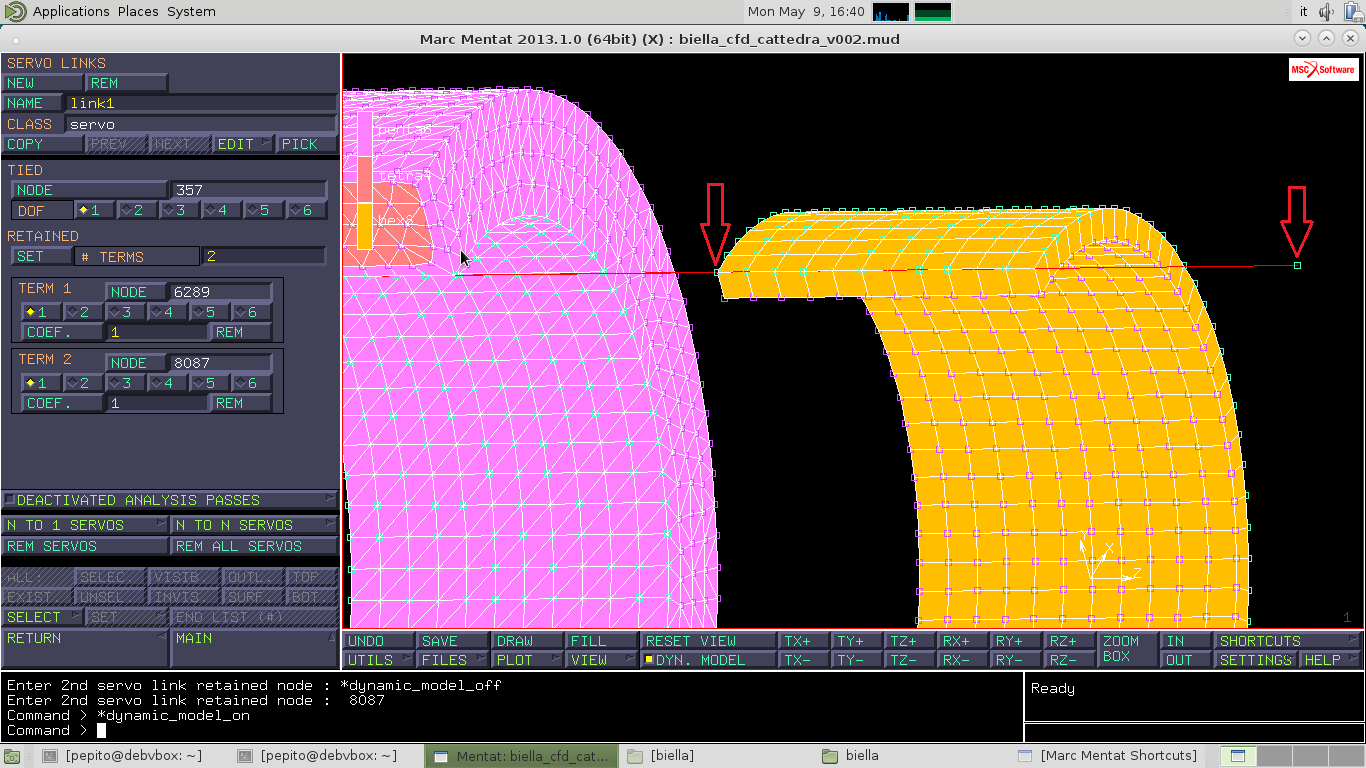
In RETAINED–># TERMS inserisco il valore 2. In TERM 1, TERM 2 seleziono il valore '1' e in COEF. digito '1', poi cliccando su NODE seleziono due nodi, uno per TERM, come in figura:

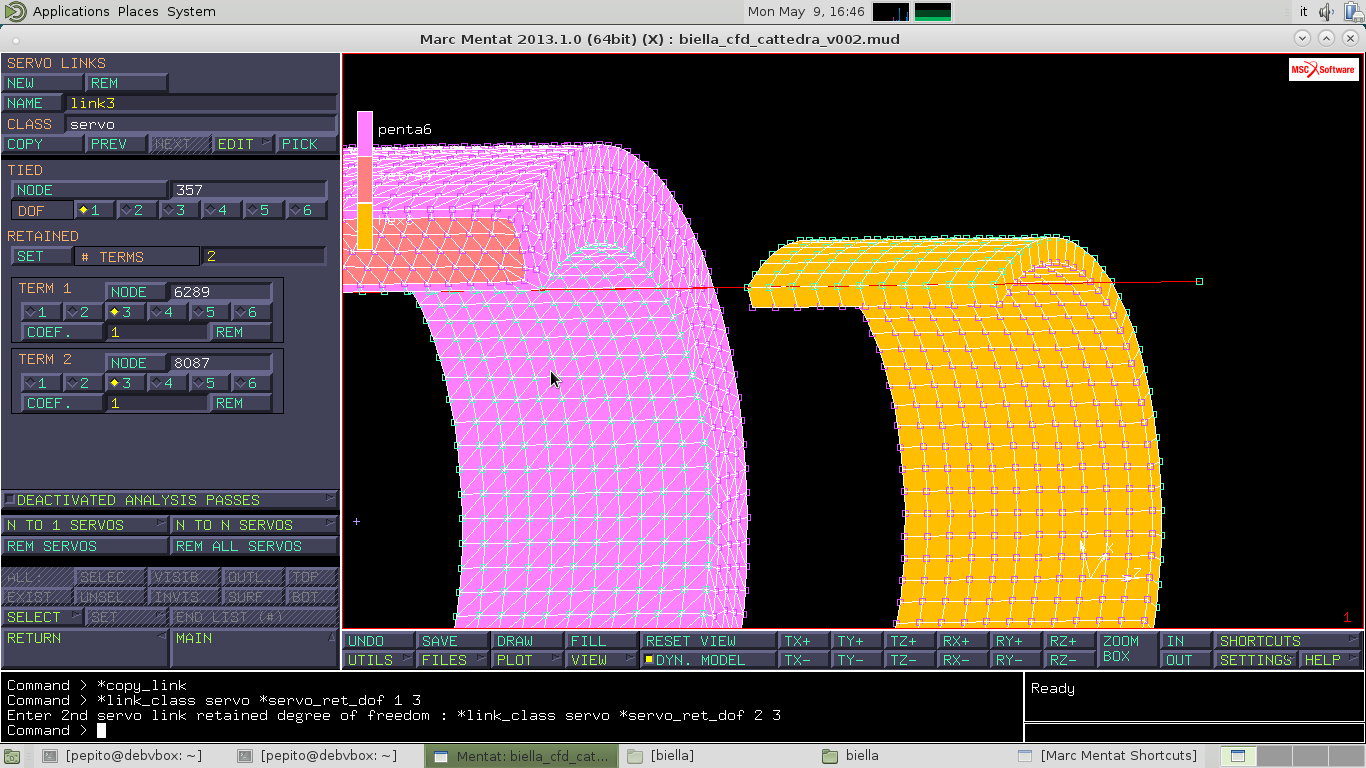
Creo altri due servolink tramite COPY, rispettivamente per il link 2 su DOF '2' e per il link 3 su DOF '3' per entrambi i TERM

Dobbiamo duplicare questi link. Torno al MAIN e vado in MESH GENERATION–>DUPLICATE, e inserisco per duplicare in direzione circonferenziale i valori '0','0','-180/35', in REPETITIONS il valore '35' e selezionandoSERVOS–>ALL EXIST do i 3 link a tutti gli altri nodi.

Per duplicare di nuovo con traslazione in $z$ pulisco il menù tramite RESET e poi inserisco in TRASLATIONS i valori '0','0','10.93/11', in REPETITIONS inserisco 11 e selezionandoSERVOS–>ALL EXIST do i 3 link a tutti gli altri nodi.

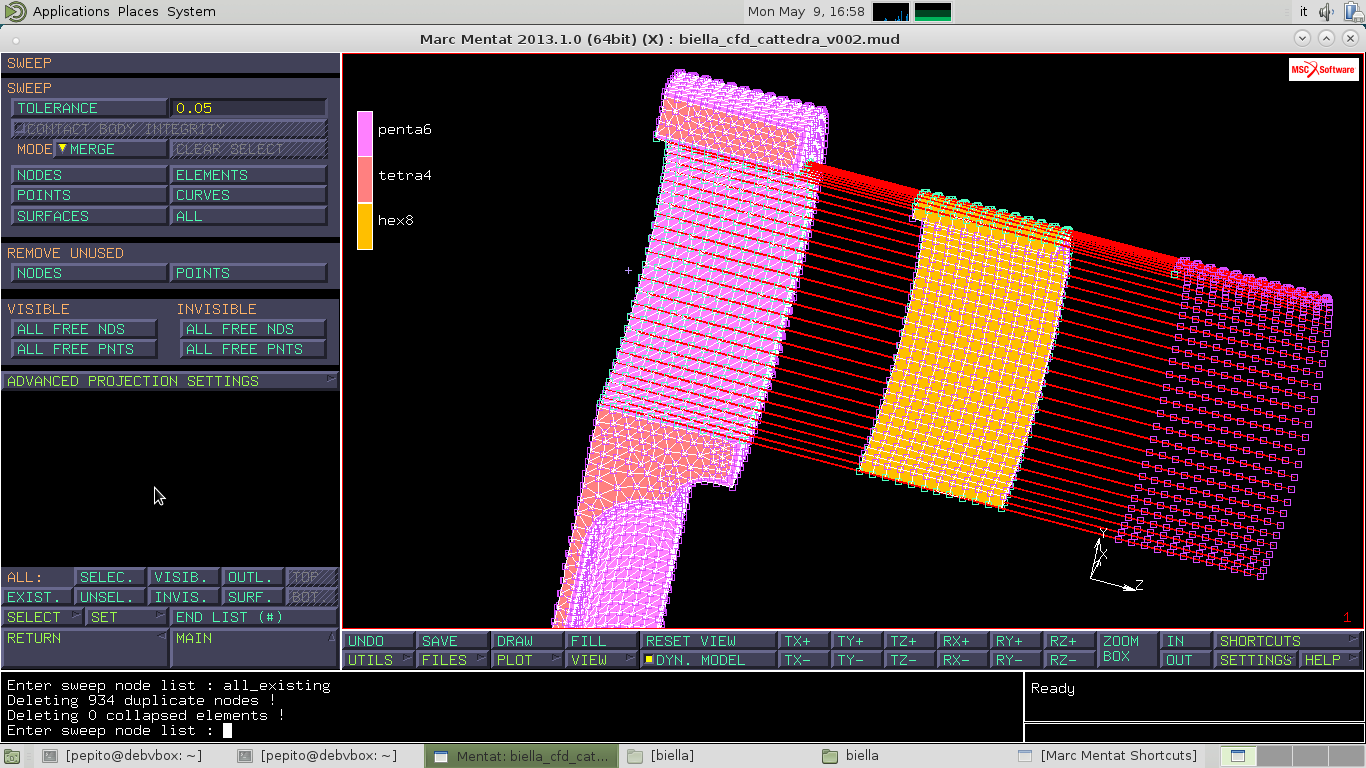
Torno al MAIN e vado in MESH GENERATION–>SWEEP e in TOLLERANCE metto il valore 0.05, poi clicco SELECT–>NODES–>ALL EXIST

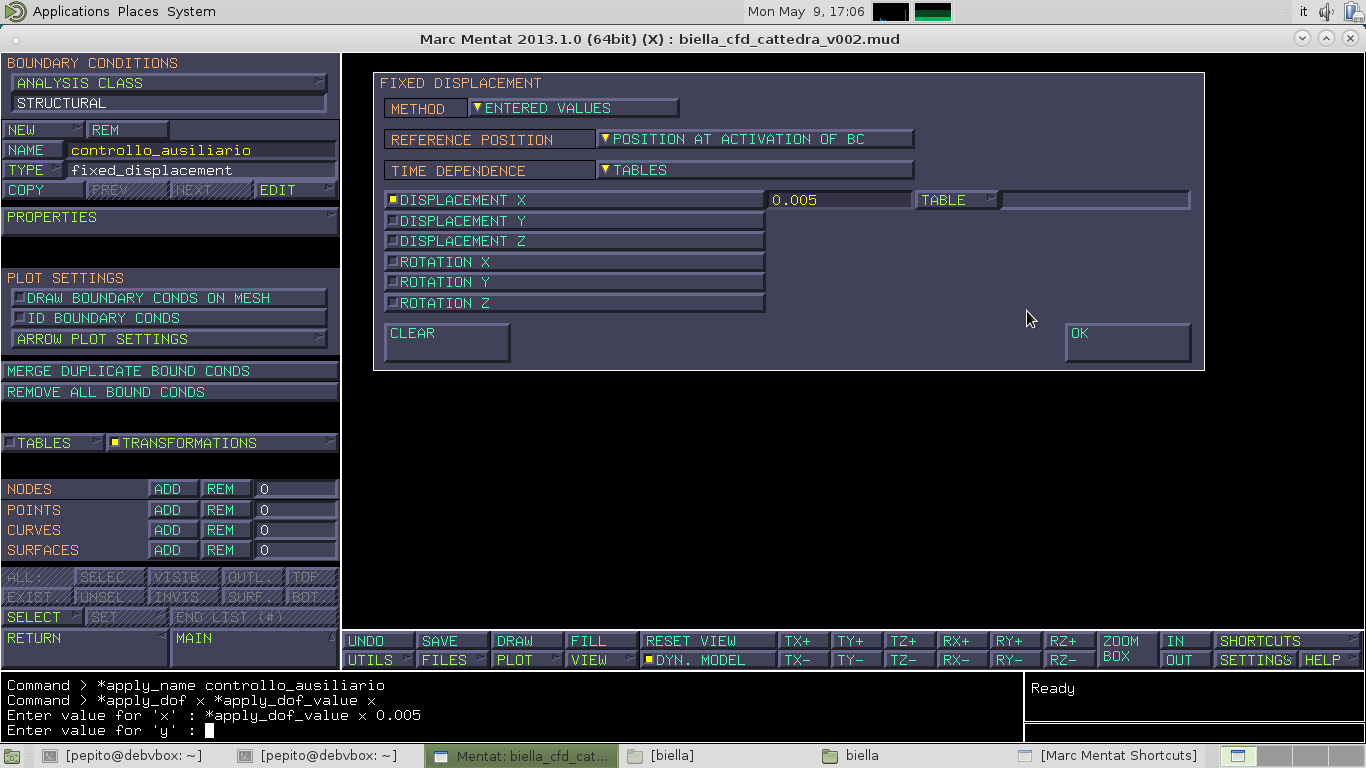
Tuttavia decido di ripetere la procedura di SWEEP con TOLLERANCE di 0.01. Voglio impostare un interferenza in assenza di attrito e procedo in questo modo. Vado al MAIN in BOUNDARY CONDITIONS–>NEW–>STRUCTURAL–>FIXED DISPLACEMENT e lo denomino 'controllo_ausiliario'.

Faccio NODES–>ADD–> e selezione come in figura:

Ottengo che

meshatura foro: 11 suddivisioni assiali, 35 sulla semicirconferenza, taglia elemento ~1mm. geometria importata piede biella 3d

mesh tipo cfd via Hypermesh (Giacopini)

biella_cfd_cattedra_v000.mud

biella_cfd_cattedra_v001.mud

biella_cfd_cattedra_v002.mud

biella_cfd_cattedra_v004.mud