Algoritmo Newton-Raphson per sistemi di equazioni non lineari: Iterazione base
Si consideri una struttura elastica con risposta non lineare, soggetta a carichi esterni che possono essere funzione della configurazione deformata. Il sistema ha n gradi di libertà, quindi scrivo: \[R(u)=F(u)\] R(u): vettore di n componenti rappresentative delle azioni da applicare dall’esterno ai gradi di libertà della struttura (se, ad esempio, i gdl sono spostamenti allora bisognerà applicare delle forze, se, invece, sono delle rotazioni applicherò delle coppie, se sono delle variazioni volumetriche applicherò delle pressioni idrostatiche) per mantenere la struttura nella configurazione deformata descritta dal vettore spostamenti nodali u.
F(u): vettore contenente le componenti delle forze nodali da applicare dall’esterno per mantenere nella configurazione di equilibrio la struttura.
Può essere, altrimenti, definita una grandezza ausiliaria r(u) chiamata residuo: \[r(u)=R(u)-F(u)\]
In configurazione di equilibrio,ovvero quando si raggiunge l'uguaglianza tra i due vettori, il residuo è nullo.
Sistemi di equazioni di questo tipo, di n equazioni in n incognite, si risolvono tramite una procedura iterativa che richiede:
- Punto/configurazione di partenza $u^{0}$ per inizializzare l’algoritmo. È preferibile che $u^{0}$ sia vicino ad $u^{*}$ (configurazione esatta che risolve il sistema di equazioni) per evitare problemi nel transito dal punto di partenza al punto di arrivo;
- Sistema iterativo $\underline{u}^{i+1}=\underline{u}^{i}-J^{i}_{r} \setminus\ \underline{r}^{i}$ . Tale sistema utilizza come matrice dei coefficienti lo Jacobiano della funzione r calcolato per $u^{i}$; inoltre, siccome la funzione r è scritta come combinazione lineare di due funzioni, possiamo scrivere anche lo Jacobiano come combinazione lineare $J_{r}|_{{u}={\underline{u}^{i}}}= J_{R}|_{u=\underline{u}^{i}} + J_{F}|_{u=\underline{u}^{i}}$. Il termine noto è rappresentato da $r^{i}$ che è funzione di $u^{i}$. Il residuo e lo Jacobiano devono essere calcolati per ogni punto in cui passo, non necessariamente per ogni punto del dominio.
- Criteri di convergenza legati alla specifica problematica strutturale.I differenti tipi di criteri di convergenza sono:
- Criterio di convergenza ai residui/ai disequilibri nodali.Con tale criterio l'iterazione si arresta quando i disequilibri sono sufficientemente bassi. Ho convergenza se ad un dato passo i, la norma $\left \| r(u^{i}) \right \|< \varepsilon ^{r}$ .$\varepsilon ^{r}$ rappresenta una soglia di riferimento assoluta. Si potrebbe anche scegliere una soglia relativa ottenuta dividendo per un valore scelto. Occorre fare attenzione al valore che si sceglie per adimensionalizzare la soglia. Ad esempio, in Marc, si divide in automatico per il modulo della massima reazione vincolare che potrebbe, però, rappresentare un problema se la reazione è nulla (ad es. nel caso di un sistema autoequilibrato in vincolamento isostatico).
- Criterio di convergenza alle incognite, che nel caso specifico diventa agli spostamenti o alla rotazioni, in base ai gdl. Si potrebbe richiedere che $\left \| u^{i}-u^{*} \right \|< \varepsilon ^{s}$ ma ciò non è possibile perché $u^{*}$ rappresenta la soluzione esatta. L’unica differenza che posso considerare è quella tra due iterati successivi, cioè $\left \| u^{i+1}-u^{i} \right \|< \varepsilon ^{s}$. L'iterazione si arresta quando due configurazioni deformate successive sono simili. Anche in questo caso posso adimensionalizzare e definire una forma relativa; ad esempio, Marc sceglie di dividere per la norma ‖u^i‖. Anche in questo caso potremmo incontrare difficoltà, ad esempio quando nel sistema ho dei moti a bassa energia potenziale elastica, cche producono elevata deformabilità della struttura, coesistenti con moti ad elevata energia potenziale elastica.
Supponiamo di avere una trave con un lungo braccio deformabile a cui è attaccata in testa una forchetta:

La deformazione macroscopica prevede una grossa rototraslazione della forchetta nello spazio. Considero il braccio piuttosto cedevole e la forchetta piuttosto rigida e ottengo la seguente deformata:
Se si usa come normalizzatore la norma degli spostamenti in assoluto, essa ha una scala adimensionale che è dovuta alla deformazione del supporto cedevole; l’equilibrio dei bracci delle forchetta, viceversa, si riferisce a scale deformative molto più piccole perché molto più rigido; per cui un lieve spostamento di apertura e chiusura di questa forchetta determina una grossa variazione delle sollecitazioni lungo la forchetta stessa. Se ammetto un errore relativo dell’ordine del 0.001, ipotizzando di avere uno spostamento dell’ordine di 100mm, l’errore ammesso risulta essere di 1/10 di mm, accettabile se riferito alla deformazione del braccio, cioè al moto a bassa energia potenziale elastica; invece, se applico lo stesso errore all'apertura o chiusura dei denti della forchetta, che hanno degli spostamenti di ordine molto piccolo, l'errore può dare grossi sbalzi tensionali e risulta, in termini assoluti, un errore considerevole anche se l’errore relativo risulta piccolo. In questo caso la deformazione, apertura e chiusura, della forchetta è un moto ad alta energia potenziale elastica perché la forchetta è rigida mentre la rototraslazione della forchetta è un moto a bassa energia potenziale elastica perché indeformabile.
In conclusione, adimensionalizzare l’errore degli spostamenti dei nodi di una zona ad alta energia potenziale elastica se deformata sugli spostamenti assoluti che sono dominati da moti a bassa energia potenziale elastica può dare, anche a fronte di errori relativi molto piccoli, degli errori assoluti molto grossi.
Il problema è ancora più evidente se si considera un caso specifico, come quello di un sollevamento di un macchinario costruito su un telaietto di supporto che ha una struttura rigida, il tutto sollevato da quattro catene.
Questo oggetto ha dei moti a bassa energia elastica, in particolare, l’oscillazione della struttura tipo altalena rispetto alle quattro catene, che vanno modellate come travi altamente flessibili, e la rotazione attorno la verticale. Il sistema è non lineare nell’ipotesi di grandi spostamenti.
Il moto della struttura nello spazio sospeso tra le quattro catene è l’elemento a bassa energia potenziale elastica mentre la deformazione del telaietto sotto il peso del macchinario che sostiene è l’elemento ad alta energia potenziale elastica associata.
Poiché l’errore relativo è adimensionalizzato sui macro spostamenti del sistema di sollevamento, la soluzione viene disequilibrata a livello di telaietto perché la convergenza è solamente sugli spostamenti, quindi, anche a fronte di un errore relativo piccolo, avendo come riferimento degli spostamenti piuttosto grossi, l’errore ammesso sugli spostamenti dei nodi del telaietto è eccessivo rispetto ai fenomeni che coinvolgono il telaietto. Il telaietto ha dei moti a bassa energia potenziale elastica quindi a bassa sollecitazione, che sono le traslazioni indicate con le frecce, più la rotazione attorno la verticale. Il telaietto può rotare o traslare con poca sollecitazione della struttura, cioè poco danno.
Un errore dell’ordine di 10mm nella rototraslazione è accettabile perché ad esso è associata poca energia elastica e poche sollecitazioni e avviene con spostamenti dell’ordine di 1000mm quindi l’errore rappresenta l’1% relativo del fenomeno di ampia deformabilità. Se considero la deformazione del telaietto stesso, cioè un errore del posizionamento relativo in una direzione data di 10mm, ottengo un momento flettente che può avere valori da cui scaturiscono stati tensionali associati molto elevati.
Anche in questo caso, perciò, c’è un grosso problema nel definire il denominatore per rendere relativo l’errore, quindi meglio considerarlo in termini assoluti, a meno che non si sia in grado di trovare un buon adimensionalizzante.
Costruzione grafica del metodo Newton-Raphson: caso monodimensionale
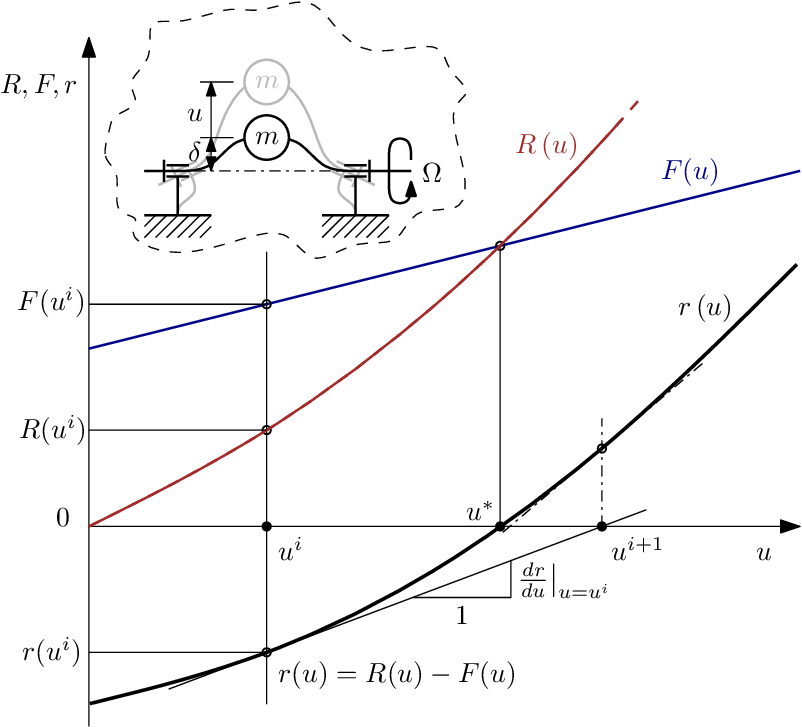
Sia u un vettore di una sola componente, perché caso monodimensionale, da considerarsi perciò uno scalare, F(u) forza funzione di uno scalare, definita dalla curva blu.
La reazione elastica della struttura è la curva in rosso R(u). La soluzione esatta corrisponde ad $u^{*}$, punto in cui le due curve si incontrano e si eguagliano. Facendo la sottrazione tra le due curve si ottiene la curva del residuo $r(u)$ in nero.
Parto da un generico $r(u^{i})$ e vado a calcolare il suo residuo definendo il punto $r(u^{i})$. In genere la curva r(u) non è data altrimenti si avrebbe già la soluzione, perciò, si calcola il residuo di $u^{i}$ che è l’unico punto visibile di tutta la curva. N-R prevede di conoscere, oltre al residuo, anche lo Jacobiano che è una matrice con tutte le derivate parziali, in questo caso, una matrice 1×1 con un unico elemento, cioè la derivata totale $\frac{\mathrm{d} r}{\mathrm{d} u}$, rappresentata graficamente tramite la pendenza della tangente. Noto il residuo e lo Jacobiano è, infatti, possibile risolvere il sistema di equazioni, associato al passo di iterazione, per via grafica, in un’unica equazione, e la soluzione non è altro che l’intersezione della retta tangente con l’asse $r(u)=0$ . Questa intersezione mi fornisce $u^{i+1}$, il successivo passo iterativo. A questo punto, è possibile ripetere la procedura partendo da questo nuovo passo.
Calcolo il residuo di $u^{i+1}$ e lo Jacobiano, cioè disegno la retta tangente, e trovo il nuovo passo successivo $u^{i+2}$ dato sempre dall’intersezione tra la retta tangente e l’asse $r(u)=0$. Ripeto l’iterazione finchè non raggiungo uno dei criteri di convergenza che ho scelto di usare.
Con riferimento alla figura sottostante si tratta il metodo di N-R applicato ad un caso bidimensionale.

Sia $\underline{r}(\underline{u})$ la funzione residuo, funzione vettoriale di componenti $r_{1}(\underline{u})$ ed $r_{2}(\underline{u})$, di variabile vettoriale $\underline{u}$, di componenti $u_{1}$ e $u_{2}$ . Il metodo di N-R si pone l’obiettivo di individuare, per via iterativa, la soluzione dell’equazione vettoriale $\underline{r}(\underline{u})=0$, rappresentativa di un sistema di 2 equazioni (nel caso in esame non lineari) in 2 variabili.
Si supponga di trovarsi all’i-esimo step di iterazione.
Nella Figura (a) sono rappresentate le due funzioni $r_{1}(\underline{u})$ ed $r_{2}(\underline{u})$ per curve di livello e la configurazione $\underline{u}_{i}$ (nota all’i-esimo step di iterazione). La soluzione che si intende avvicinare il più possibile mediante il metodo di N-R è rappresentata dal punto $\underline{u}^{*}$, per il quale $r_{1}(\underline{u})$ ed $r_{2}(\underline{u})$ si annullano.
Si tenga presente però che tali curve non sono note al risolutore, il quale conosce soltanto:
- il valore che esse assumono in $\underline{u}^{i}$
- il valore di tutti gli elementi della matrice Jacobiana di $\underline{r}(\underline{u})$ calcolata in $\underline{u}=\underline{u^{i}}$
Per procedere si individuano due piani, rispettivamente tangenti alle curve $r_{1}(\underline{u})$ ed $r_{2}(\underline{u})$,nella configurazione $\underline{u}_{i}$:
- $T_{1}^{i}(\underline{u})$ è tangente ad $r_{1}(\underline{u}=\underline{u}^{i})$
- $T_{2}^{i}(\underline{u})$ è tangente ad $r_{2}(\underline{u}=\underline{u}^{i})$
Nota:
Per individuare un piano sono in generale necessari tre elementi: un punto dello spazio per cui passa il piano e due coefficienti ad indicarne l’inclinazione, tutti noti per ipotesi.
Nel caso del piano $T_{1}^{i}(\underline{u})$ il punto di passaggio è $( \underline{u}^{i} , r_{1}(\underline{u}=\underline{u}^{i}) )$, ed i due coefficienti sono gli elementi della prima riga dello Jacobiano di $\underline{r}(\underline{u})$, $$\begin{bmatrix}\frac{\partial r_{1}}{\partial u_{1}} & \frac{\partial r_{1}}{\partial u_{2}} \\ \frac{\partial r_{2}}{\partial u_{1}} &\frac{\partial r_{2}}{\partial u_{2}} \end{bmatrix}$$ calcolata per $\underline{u}=\underline{u}^{i}$.
Nel caso del piano $T_{2}^{i}(\underline{u})$ il punto di passaggio è $( \underline{u}^{i} , r_{2}(\underline{u}=\underline{u}^{i}) )$, ed i due coefficienti sono gli elementi della seconda riga dello Jacobiano di $r(\underline{u})$ $$\begin{bmatrix} \frac{\partial r_{1}}{\partial u_{1}}&\frac{\partial r_{1}}{\partial u_{2}} \\ \frac{\partial r_{2}}{\partial u_{1}}&\frac{\partial r_{2}}{\partial u_{2}} \end{bmatrix}$$ calcolata per $\underline{u}=\underline{u}^{i}$.
Nella Figura (b) sono rappresentati i due piani tangenti $T_{1}^{i}(\underline{u})$ e $T_{2}^{i}(\underline{u})$ con curve di livello, che nel caso di piani sono sempre rettilinee,completamente note .
La linea di livello di valore $T_{1}^{i}(\underline{u})=0$, rappresenta il luogo dei punti tali per cui la forma linearizzata della funzione prima componente del residuo si annulla (cioè si annulla il piano tangente alla prima componente del residuo, nel punto $( \underline{u}^{i} , r_{1}(\underline{u}=\underline{u}^{i}) )$.
Si può dire lo stesso per la linea di livello di valore $T_{2}^{i}(\underline{u})=0$.
Siccome tali curve di livello sono rette, per trovare il punto di incontro delle due curve di valore zero sarà dunque sufficiente risolvere un sistema di due equazioni lineari in due incognite. Le incognite in questione non sono altro che le componenti di $\underline{u}^{i+1}$ punto del piano $(\underline{u}_{1} , \underline{u}_{2})$, punto di nuova iterazione.
Allo step successivo (i+1-esimo) si dovranno nuovamente individuare due piani, rispettivamente tangenti alle curve $r_{1}(\underline{u})$ ed $r_{1}(\underline{u})$, nella nuova configurazione $\underline{u}^{i+1}$ :
- $T_{1}^{i+1}(\underline{u})$ è tangente ad $r_{1}(\underline{u}=\underline{u}^{i+1})$
- $T_{2}^{i+1}(\underline{u})$ è tangente ad $r_{2}(\underline{u}=\underline{u}^{i+1})$
Si dovrà poi graficare tali piani secondo curve di livello (di forma rettilinea e completamente note) ed individuare il punto di incontro delle curve rettilinee a valore nullo. Sarà poi possibile procedere al calcolo di $\underline{u}^{i+2}$ mediante la risoluzione di un nuovo sistema lineare.
L’iterazione proseguirà, così come descritto, sino al raggiungimento dei criteri d’arresto inizialmente imposti.
Nel caso di figura si noti come la configurazione $\underline{u}^{i+1}$ sia più vicina della $\underline{u}^{i}$ alla soluzione $\underline{u}^{*}$, sintomo del fatto che il metodo sta convergendo al risultato cercato. Non è tuttavia possibile conoscere a priori se il metodo convergerà o meno alla soluzione.
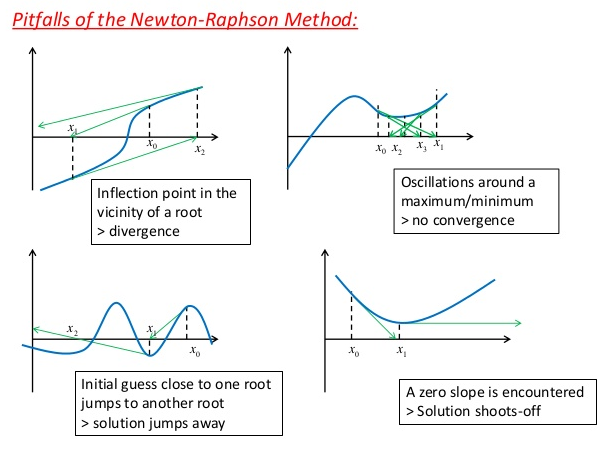
Nel caso monodimensionale il metodo può non risultare convergente per diverse motivazioni di semplice rappresentazione:
Si noti per esempio il caso, citato anche in aula, in cui nell’iterazione si incontra un punto della funzione a tangente orizzontale. L’estensione bidimensionale di questa condizione è rappresentata da una matrice Jacobiana completamente nulla, in uno dei punti di campionamento.
In realtà il metodo per il caso 2D non converge anche quando la matrice Jacobiana è singolare nel punto di campionamento. In questo caso esiste una retta appartenente ad uno dei piani tangenti che è parallela al piano $u_{1}u_{2}$ ( e che quindi non lo interseca mai ). Muovendosi quindi lungo la direzione individuata da tale retta la si ha quindi una componente del residuo che non cambia (non cambiano le reazioni elastiche oppure la variazione delle reazioni elastiche è completamente compensata dalla variazione delle forze esterne, funzione della configurazione. In altri termini si presenta una condizione di equilibrio indifferente).
Come si è potuto notare, il caso 2D è di non semplice rappresentazione, tuttavia è stato portato come esempio poiché rappresentativo dei casi più generali N-Dimensionali. In particolar modo il caso monodimensionale è di grande chiarezza grafica e didatticamente utile per comprendere il metodo, tuttavia l’insieme $\mathbb{R}$ è un insieme ordinato mentre $\mathbb{R}^{2}$ e di $\mathbb{R}^{n}$ che non sono propriamente ordinabili.
Nel caso specifico dell’albero rotante, visti i problemi del N-R decido di doverlo “aiutare”.
Non pretendo di risolvere il sistema direttamente per la velocità di rotazione $\Omega$, perché per passare dallo stato per $\Omega=0$ (soluzione indeformata) allo stato finale $\Omega$, il salto è troppo grande e il N-R non converge. Decido pertanto di inventarmi una fittizia successione temporale, definendo una $\Omega(t)$, dove il tempo è giusto una variabile con cui modulare le soluzioni applicate, anche perché effettivamente nel problema non c’è nulla in funzione del tempo.
Definisco una funzione $\Omega$ che cresce lentamente in maniera lineare, (essendo che di solito sono le forze a crescere in maniera lineare), faccio crescere linearmente $\Omega^{2}$ .
Invento una successione temporale della mia sollecitazione; parto sempre con $u_{0}$, (primo tentativo del N-R, configurazione indeformata) che è soluzione del sistema scarico.
Partendo da qui, con un piccolo carico, probabilmente il N-R riesce a risolverlo; quindi sostanzialmente, anche se il mio carico deve essere svolto a quel valore di $\Omega^{2}$, non lancio il N-R direttamente a quel valore finale, ma definisco tanti piccoli passi incrementali a livello di carico.
Definisco una $\Omega(tj)=\Omega_{j}$ e definisco una $\underline{u}^{i}_{j}$ i-esimo passo del N-R. Considero quindi $\underline{u}^{0}_{0}=\underline{0}$ con i=0 e j=0 (soluzione di $\Omega_{0}=0$) che chiamo anche $\underline{u}^{*}_{0}$ indeformata della soluzione esatta del carico nullo.
Pongo il problema di risolvere $\Omega_{1}$, e mi serve definire un’ iterazione per questo primo livello di carico: definisco $\underline{u}^{0}_{1}=\underline{u}^{f in}_{0}$ che intendo come 1° iterato dall’ultimo corretto precedente, in generale $\underline{u}^{0}_{j+1}=\underline{u}^{f in}_{j}$ .
Definisco quindi tanti livelli di carico, e per ogni salto di livello di carico eseguo un iterazione di N-R: quindi due iterazioni unificate, una che scorre su livelli di carico e una che prevede l’iterazione di N-R.
Come funziona? Di seguito poniamo uno schema grafico associato al problema precedentemente trattato.
F(u) è la forza associata ad un dato valore di $\Omega$ in questo caso poniamo F(u) associato a $\Omega_{j+1}$ , e il valore della forza associato ad un omega minore (è la retta con la pendenza minore) che è F(u), $\Omega_{j}$, dove possiamo anche dire: $\Omega_{j+1}>\Omega_{j+1}$, con omega partito da un valore nullo, e arriverà ad un valore finale, che è la velocità con cui gira effettivamente l’albero.
Non lancerò pero N-R sul salto da configurazione indeformata al valore di $\Omega$ finale, ma lo “aiuto” facendo il salto gradatamente. La reazione del sistema è R(u), che combinata con la forza mi dà la soluzione esatta $\underline{u}_{j}^{*}$ a livello di carico j.
Suppongo di aver già lanciato N-R e di aver ottenuto la convergenza per il livello di carico j, ( $\underline{u}_{j}^{*}$ come soluzione esatta è un risultato teorico), quindi quello che ho in effetti è un’approssimazione di questo $\underline{u}_{j}^{*}$ .
Lancio N-R sul valore di $\underline{u}_{j}^{*}$ e mi fornisce un valore di $\underline{u}_{j}^{fin}$ con $\underline{r}(\underline{u}_{j}^{f in})\neq 0$; quindi diciamo che ogni iterato di N-R lanciato ad un determinato salto di livello di carico non mi fornisce una soluzione esatta, ma affetta da errore: c’è uno scostamento a livello di spostamento di soluzione esatta e uno a livello di residuo sulla soluzione esatta.
Quindi utilizzo $\underline{u}_{j}^{f in}$ come punto di partenza per ricavare $\underline{u}_{j+1}^{0}$ e N-R per livelli di carico successivo lo faccio partire da questo valore, che sul grafico è rappresentato come la curva di residuo.
Per disegnarla parto dal valore $\underline{u}_{j+1}^{0}$ e il successivo calcolato sulla verticale, il sistema ha soluzione esatta nel punto in cui si annulla la funzione, quindi la curva in nero è il residuo calcolato come: $$r(u,t_{j+1})=R(u)-F(u,t_{j+1})$$
$\underline{u}_{j+1}^{0}$ diventa il mio nuovo $u_{0}$ nel passaggio dal livello di carico j al livello di carico j+1; da qui parto, faccio il N-R e ottengo il valore $\underline{u}_{j+1}^{1}$, e così via fino ad arrivare al valore al $\underline{u}_{j+1}^{f in}$.
Nella procedura di N-R non vi è accumulo di errore, perché sono partito da un $u_{0}$ affetto da errore, ma per N-R questo può essere un punto a piacere, quindi non essendoci alcuna restrizione sul punto di partenza, non mi influisce sul risultato finale (può al massimo non convergere, ma se convergo non ho accumulato errore).
Ciò si verifica a meno che il sistema non sia “historic-dipendent”, ossia che la soluzione del sistema non sia soluzione dello storico.
AUTORI
Luca De Lorenzis, mat.104170, Francesca Palano, mat. 103804, Diego Zambelli, mat. 105031, Asia Marcello, mat.104394.