Nella lezione n° 12 è sorta la necessità di stoccare una matrice di rigidezza in forma Bandata. L’utilizzo di questa matrice permette un notevole risparmio in termini di costo computazionale in quanto composta da soli termini non nulli della matrice di rigidezza “piena”. Questa matrice ha un numero di righe pari al numero di gradi di libertà del sistema ed un numero di colonne pari alla larghezza di banda. Al più (condizioni sfavorevoli della numerazione nodale) si ottiene una matrice delle stesse dimensioni della matrice piena. Come fatto precedentemente ci proponiamo di effettuare il vincolamento della matrice in forma bandata.

Figura 1

Il codice fortran riportato vuole presentare l’algoritmo necessario a risolvere il nostro problema. Il processo di vincolamento è lo stesso, ma la subroutine deve essere riadattata per poter lavorare con una matrice in forma bandata. La descrizione di tutti gli elementi presenti nel suddetto codice è stata affrontata nella lezione 12. Sia idof il grado di libertà che intendiamo vincolare e val il valore imposto al grado di libertà idof-esimo.

Il codice si divide in tre step:

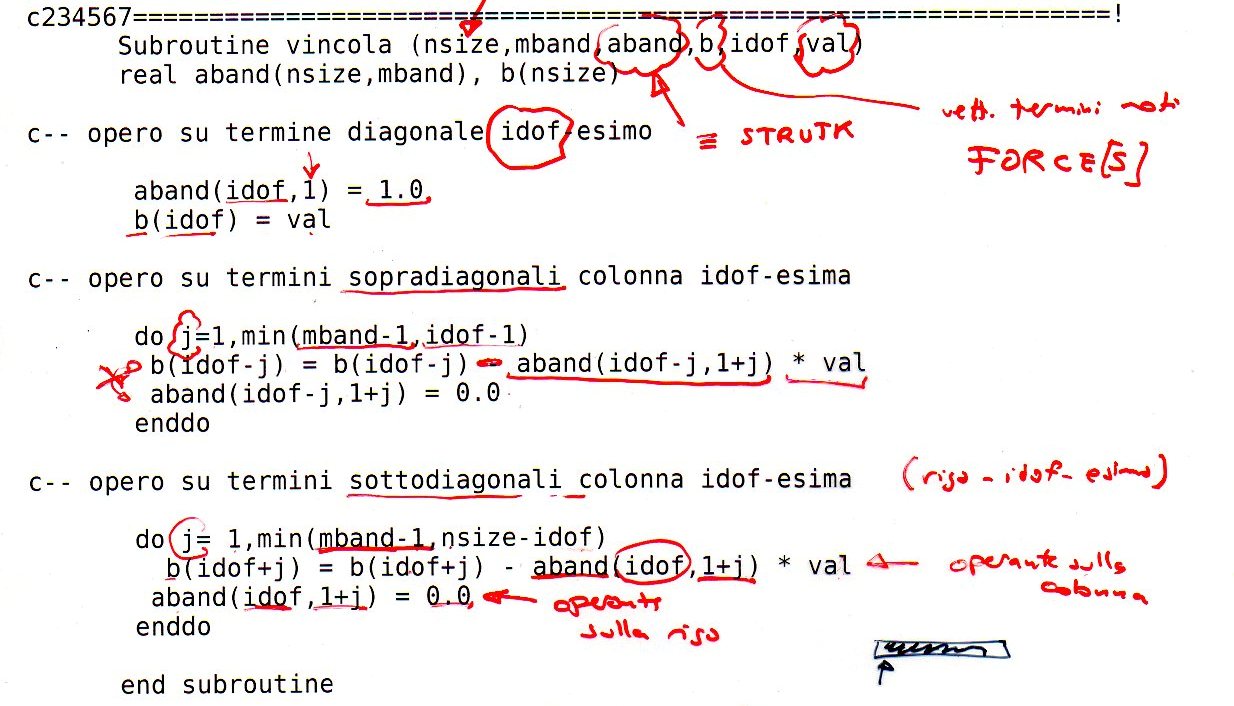
• aband(idof,1)=1.0 assegna il valore unitario al termine di riga idof e colonna 1 (termine diagonale nella matrice piena); b(idof)=val assegna il valore val al termine idof-esimo del vettore delle forze b.

A questo punto è necessario azzerare tutti gli elementi sopra-diagonali e sotto-diagonali dell’idof-esima colonna (sotto-diagonali e sopra-diagonali dell’idof-esima riga). Non è possibile procedere subito con l’azzeramento in quanto si perderebbe il contenuto delle celle considerate. Passiamo l’informazione al termine noto.

• b(idof-j)=b(idof-j)-aband(idof-j,1+j)*val : assegna al termine idof-j del vettore b il valore già contenuto in esso e sommato al termine sopra-diagonale dell’idof-esima colonna, moltiplicato per val e cambiato di segno. Considerato l’elemento idof si va ad operare sugli elementi a 45° in quanto corrispondenti degli elementi sopra-diagonali dell’idof-esima colonna della matrice piena. Si prosegue con l’azzeramento dei termini considerati.

• b(idof+j)=b(idof+j)-aband(idof,1+j)*val: assegna al termine idof+j del vettore b il valore già contenuto in esso e sommato al termine sotto-diagonale dell’idof-esima colonna, moltiplicato per val e cambiato di segno. Considerato l’elemento idof si va ad operare sugli elementi alla destra di esso in quanto corrispondenti degli elementi sotto-diagonali dell’idof-esima colonna della matrice piena. Si prosegue con l’azzeramento dei termini considerati.

Figura 2

Il ciclo consta di due cicli do separati utilizzati per trattare rispettivamente gli elementi sopra-diagonali e sotto-diagonali dell’idof-esima colonna in cui scorre un indice $j$. Questo indice scorre da 1 al minimo tra due grandezze che indicano i limiti da non superare per rimanere all’interno della banda e della matrice piena. Pertanto si dovrà operare finchè c’è banda e finchè c’è matrice. Si vuole evitare sostanzialmente di andare ad operare con termini che sono fuori banda o che addirittura non esistono.

Figura 3 e 4

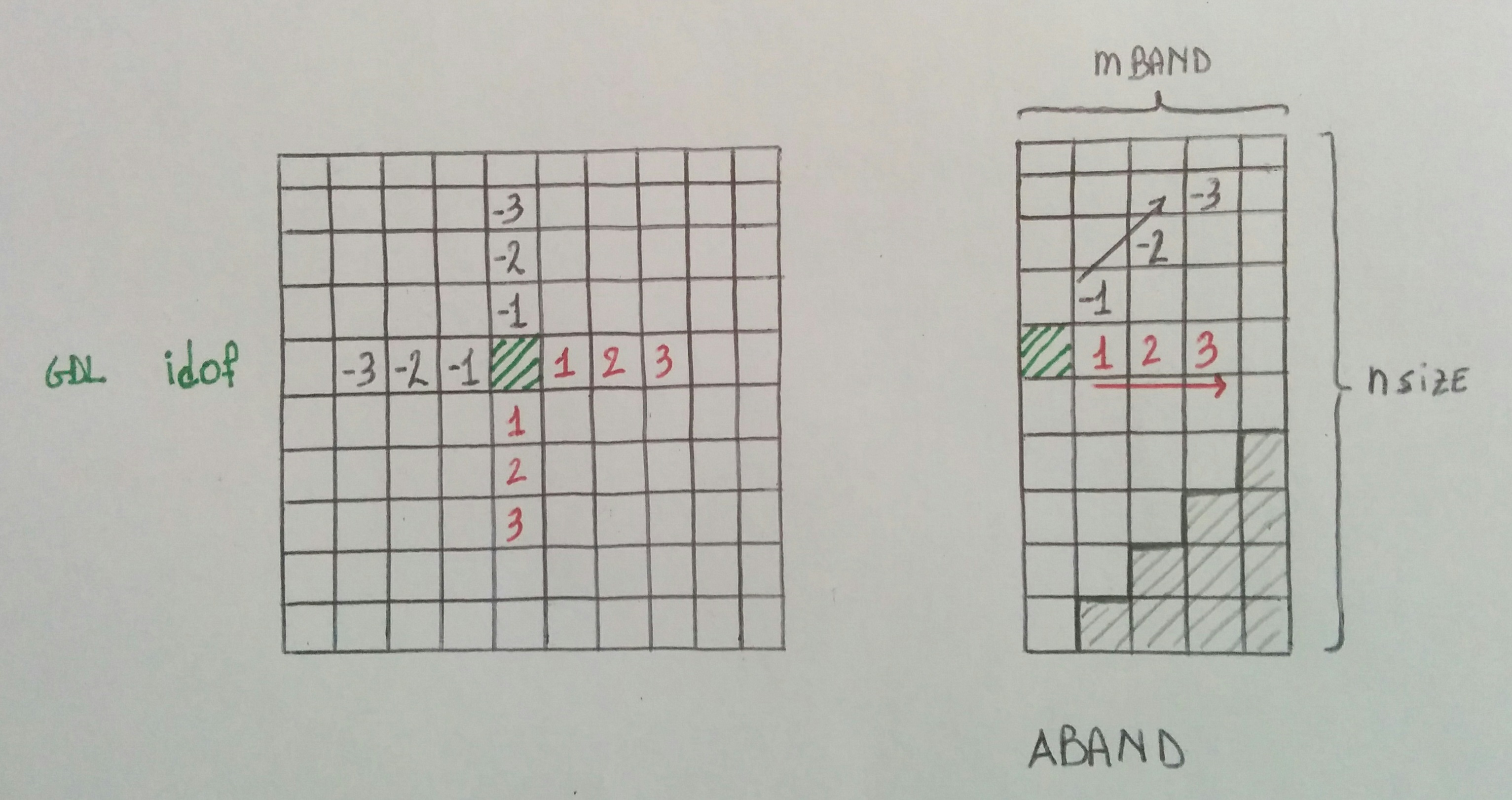
Per esempio, osservando la matrice bandata di figura 3, se dovessi partire dalla posizione P1, ci potrebbe essere la possibilità di incappare in un “fuori matrice” mentre il codice sta operando sugli elementi sottodiagonali (della corrispondente matrice piena). Si dovrà pertanto rispettare il limite più restrittivo tra mband-1 e idof-1 e ciò viene garantito e controllato dal comando do j = 1, min (mband - 1, idof - 1). Se invece ci trovassimo nella posizione P2, il problema, analogo al precedente, si verificherebbe quando il codice andrebbe a lavorare sugli elementi sopradiagonali della corrispondente matrice piena. Anche in questo caso il tutto viene impedito da do j = 1, min (mband - 1, nsize - idof). Si dovrà pertanto rispettare il limite più restrittivo tra mband-1 e idof-1(nsize-idof nello step 3), in modo tale da non “sforare” il boundary della matrice piena Per quanto riguarda il vettore delle forze b possiamo osservare ( figura 4) che non tutti i suoi termini vengono modificati: partendo dall’idof-esimo elemento, b riceve modifiche sicuramente sugli mband-1 elementi verso l’alto e verso il basso. Ma cosa succede ai restanti elementi (contrassegnati da ?)? Essendo tutti nulli non avrebbe senso operarci, così il codice si ferma in anticipo guadagnando in tempo e memoria anche se la forma logica del programma risulta un po’ più complessa. Non sempre forme logiche più complesse risultano più efficaci: la complessità potrebbe richiedere anch’essa un grande sforzo computazionale pur ottimizzando in maniera migliore la memoria. Si può ragionevolmente pensare che il costo computazionale su una matrice bandata sia proporzionale ad $m^2*n$, mentre quello di una matrice piena ad $n^3$ con $m$ larghezza di banda ed $n$ numero di incognite.

Immagine proiettata

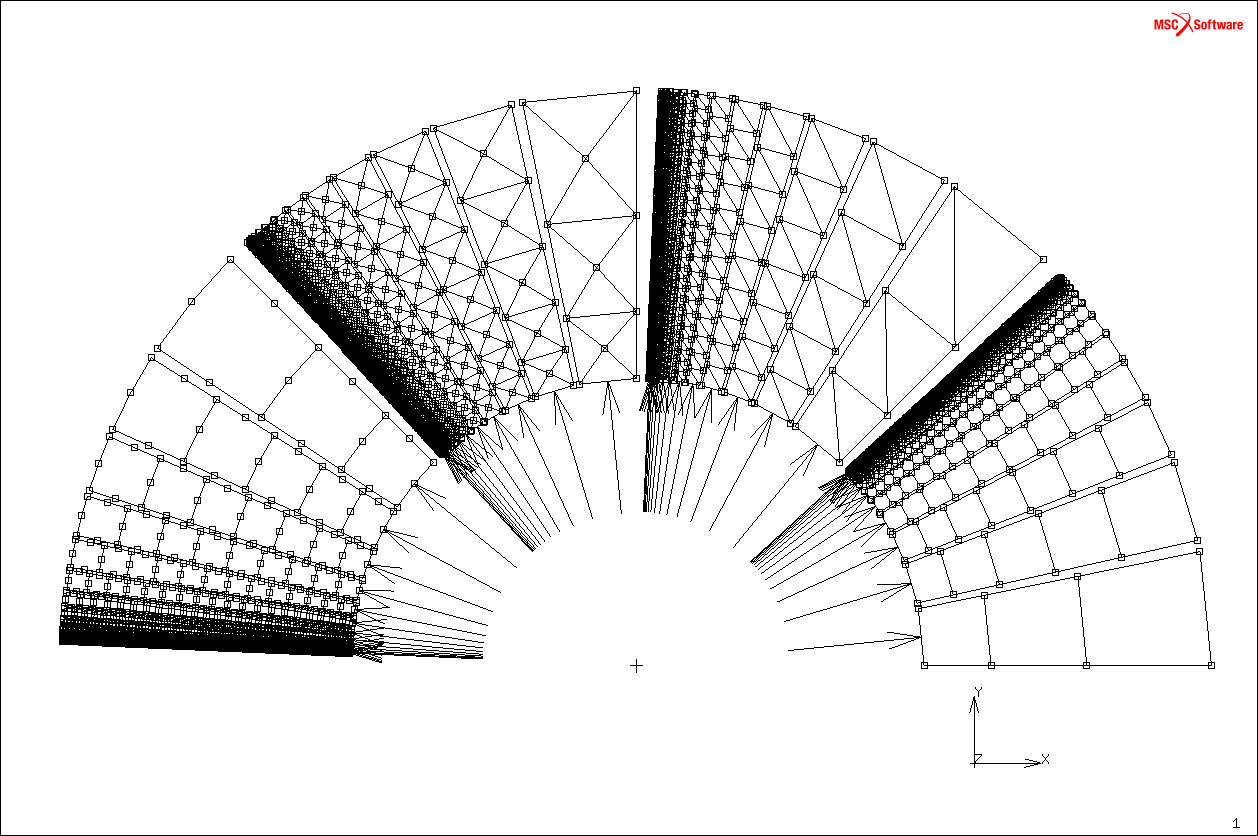
NOTA: il vincolamento della mesh tria3 asimmetrica è migliorabile!!

Per quanto riguarda il tubo in pressione, modellato in laboratorio con ipotesi di Defermazione Piana ($\epsilon_{z}=0$), si deve ricordare che non sempre tale ipotesi, soprattutto per materiali pieni, risulta sempre esatta e corretta. Prendiamo, ad esempio, un tubo (nella figura 5 in sezione frontale) con un foro sottoposto alla pressione $P_i$ e come pressione esterna quella ambiente ($P_e=0$). In queste condizioni, adottare una modellazione in D.P. non risulterebbe corretto: infatti, pressurizzando il foro, si verrebbe a creare una zona (righe nere) caratterizzata da una $\epsilon_{z}<0$ (causa effetto Poisson), ma non nulla, a differenza della restante zona, lontana dal foro, in cui $\epsilon_{z}\sim 0$. Ciò dimostra che lavorare in D.P. sulla sezione è spesso una situazione particolare quanto rara. Un altro esempio potrebbe essere rappresentato dal pezzo in figura 6: pressurizzando il primo foro (il primo da sinistra), la zona circostante andrebbe in trazione per effetto Poisson, generando una $\epsilon_{z}<0$, al contrario delle altre aree in cui $\epsilon_{z}\sim 0$. Ciò comporterebbe una leggera inflessione del pezzo in lunghezza che cozzerebbe con le ipotesi da noi fatte nella modellazione. Anche questo secondo esempio dimostra quanto l’utilizzo di D.P. (e T.P.) nei modelli studiati sia delicato.

Figura 5

Figura 6

Risultati Tubo in Pressione Mark/Mentat

Modello MSC.Marc verifica convergenza tubo prova_convergenza_v1.mud

Foglio di calcolo convergenza_errore_fem_v2.ods