Appunti prof. Giavotto su piastre sottili

Le piastre sono corpi o parte di corpi in cui una dimensione risulta molto più piccola delle altre due. Per definire la condizione per cui uno spessore è piccolo, lo si confronta con una delle due altre dimensioni caratteristiche (l). Dato uno spessore $h$, esso risulta piccolo se $(h/l)<<1$.

Per poter modellare un elemento in teoria della piastra, devo avere la possibilità di definire un piano medio. Sommando le estensioni sopra e sotto il piano medio posso poi definire uno spessore. La teoria da risultati affetti da errore maggiore al crescere dello spessore.
Non esiste un valore univoco per valutare dal rapporto $(h/l)$ se si tratti o meno di una piastra; la definizione varia di caso in caso.

Esistono due teorie delle piastre:

1. Teoria alla Kirchhoff, in cui le piastre non ammettono deformazione a taglio.
   
2. Teoria alla Reissner-Mindlin, in cui la piastra deforma anche a taglio (usata nella teoria degli elementi finiti).
   

Per individuare il piano medio di una struttura posso utilizzare il seguente algoritmo. Si considera un punto qualsiasi disposto sulla superficie superiore (P) e si valuta il punto più vicino sulla superficie opposta in termini di distanza euclidea (S). Per la metà del segmento (PS) che congiunge i due punti passerà il piano medio.

La teoria della piastra si basa su un'ipotesi cinematica in analogia con la teoria della trave.
Nella teoria della trave a flessione si suppone che i punti appartenenti alle sezioni della trave, ottenute per intersezione di un piano normale all'asse baricentrico, restino su questo piano (Ipotesi che va bene per la flessione e lo sforzo normale, in misura minore per il taglio). Suppongo inoltre che i punti non si muovano sul piano (trascurando eventuali effetti Poisson) e che le rototraslazioni nel punto d'intersezione del piano e dell'asse baricentrico definiscono completamente il moto dei punti di tutta la sezione.

In parallelo utilizzo un piano di riferimento arbitrario (ad esempio il piano medio) su cui scelgo un punto e considero la retta normale alla superficie passante per il punto: ottengo un segmento di spessore pari alla parete sottile.
Impongo sul segmento le stesse condizioni cinematiche sopra citate, applicate sulla sezione di trave. Per ogni punto P interno al materiale elastico, posso trovare la proiezione Q sul piano di riferimento.
In particolare:

• P resta sempre allineato a Q, anche nella configurazione deformata;
• la distanza tra P e Q non varia;
• il moto di P è definito in maniera sufficiente dalle rototraslazioni del punto Q;
• se Q ruota, allora tutto il segmento segue la rotazione.

Per comodità si considerano rotazioni piccole (errore ingegneristico irrilevante) per poter approssimare con Taylor le funzioni trigonometriche.

Consideriamo il segmento normale alla superficie di riferimento.

• Secondo Kirchhoff esso resta normale alla superficie anche nella deformata.
• Secondo Reissner-Mindlin si ammette che esso s'inclini rispetto alla superficie; l'entità dell'inclinazione è legata alla deformata tagliante media lungo lo spessore.

Analizzo una piastra tozza, incastrata e collegata a un oggetto traslante in direzione verticale. L'elemento elastico si deforma “a mazzo di carte” poiché tozzo (se fosse sottile si deformerebbe a “s”)

La deformazione tagliante è l'inclinazione che un segmento prende rispetto alla superficie media, in figura indicato con γ₃₁.

Nelle ipotesi di Reissner-Mindlin γ₃₁≠ 0.
Nelle ipotesi di Kirchhoff γ₃₁=0, ossia non c'è deformazione a taglio. Questo non vuol dire che non ci sia tensione tagliante. Sarà il modulo di rigidezza infinito ad annullare la γ.

Definisco un sistema di assi, con il terzo asse normale alla superficie media (asse z). L'asse z non è un asse globale, ma locale, perché è definito localmente (soprattutto se la superficie è curva).

Preso un elemento finito come l'isoparametrico a 4 nodi, la direzione normale può essere ricavata dalla direzione perpendicolare ad ambo le diagonali dell'elemento.

Definisco allora tre componenti di spostamento:

• u, spostamento in direzione x;
• v, spostamento in direzione y;
• w, spostamento in direzione z.

Analizzando la figura successiva, provo a scrivere gli spostamenti del punto P in base alle rototraslazioni di Q sul piano di riferimento.

Definisco u,v,w, spostamenti di Q. In particolare w=w, poiché per piccole rotazioni cosθ≈1 (w-w=1-cosθ).

Le relazioni tra gli spostamenti di P e Q risultano:

• u=u+φ_y
• v=v+φ_x
• w=w

Non ho φ_z in quanto è una rotazione del segmento attorno al proprio asse.

Una piastra programmata secondo la teoria di Kirchhoff o di Mindlin non reagisce elasticamente a una rotazione dei suoi punti nel continuo (o dei suoi nodi, negli elementi finiti) in direzione normale alla superficie media. Questo moto è detto Moto di Drilling (di foratura).

Occorre tenerne conto nella modellazione, in quanto non risulta possibile applicare una coppia sul nodo che non ha reazione elastica.
Per tamponare questo grado di libertà posso aggiungere sul nodo una molla torsionale, di rigidezza arbitraria.

Ora devo decidere se procedere con la teoria alla Kirchhoff o alla Mindlin.
Se procedo con Mindlin,le rotazioni e gli spostamenti sono entità che rimangono indipendenti, tanto che posso modellare correttamente la deformata a taglio. Se invece utilizzo la teoria di piastra alla Kirchhoff, non ci può essere alcuno scostamento tra rotazioni φ_x e φ_y e le derivate degli spostamenti trasversi la piastra in z.

Decido di adottare la teoria di piastra alla Kirchhoff, per cui definisco le rotazioni, indipendenti tra loro, come:

• $\varphi_x=-\frac{\partial w}{\partial x}$
• $\varphi_y=-\frac{\partial w}{\partial y}$

In questo modo però,attraverso le relazioni viste, perdo l'indipendenza delle rotazioni dagli spostamenti infatti attraverso la teoria di Kirchhoff si può determinare lo spostamento complessivo (u,v) di un punto qualunque di una sezione di un concio di piastra come la somma dello spostamento del baricentro di questa sezione e lo spostamento dato dalle rotazioni della stessa, esprimibile come:

• $w=w(x,y)$
• $u=u_0+z \cdot \tan (\varphi_x) \approx u_0+z \cdot \varphi_x = u_0 - z \cdot \frac{\partial w}{\partial x} $
• $v=v_0+z \cdot \tan (\varphi_y) \approx v_0+z \cdot \varphi_y = v_0 - z \cdot \frac{\partial w}{\partial y}$

Dagli spostamenti si può giungere facilmente al calcolo delle deformazioni:

$\varepsilon_x =-\frac{\partial u}{\partial x} = \frac{\partial u_0}{\partial x} - z \cdot \frac{{\partial}^{2} w}{{\partial x}^{2}}$

$\varepsilon_y =-\frac{\partial v}{\partial y} = \frac{\partial v_0}{\partial y} - z \cdot \frac{{\partial}^{2} w}{{\partial y}^{2}}$

$\gamma_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} = \frac{\partial u_0}{\partial y} + \frac{\partial v_0}{\partial x} - 2 z \cdot \frac{{\partial}^{2} w}{\partial x \partial y}$

Queste relazioni valgono per ogni punto della struttura, differendo unicamente per la quota z,che risulterà, in base alle notazioni scelte, positiva se sopra la superficie di riferimento, negativa se viceversa. A queste relazioni si può associare un vettore K delle curvature K_i

$K_x= -\frac{{\partial}^{2} w}{{\partial x}^{2}} ;\hspace{2cm} K_y= -\frac{{\partial}^{2} w}{{\partial y}^{2}} ;\hspace{2cm} K_{xy}= -\frac{{\partial}^{2} w}{\partial x \partial y} $

$$\underline{K}= \begin{bmatrix} K_x \\ K_y \\ K_{xy} \\ \end{bmatrix}$$

Considerando deformazioni uniformi lungo tutta la piastra, allora si dovranno considerare curvature uniformi. Ma questo ragionamento non è sempre garantito, infatti si complica notevolmente nel caso in cui si studiassero elementi a piccolo spessore.

Per l’ipotesi cinematica si prevede che le deformazioni siano valide linearmente su tutta la piastra e la teoria di di tensione piana prevede una libera deformazione in direzione Z, poiché non esistono tensioni che la ostacolino. Sappiamo però dalla teoria di Kirchhoff che le sezioni perpendicolari al piano medio rimangono indeformate, impedendo che si generino delle strizioni in direzione Z (come nella teoria della trave dove tipicamente è uguale a zero). Allora per non entrare nel contraddittorio, in modo da semplificare la trattazione con l'introduzione della matrice di tensione piana, utile ad esprimere il legame tensioni-deformazioni, si pensa dividere la piastra in strisce infinitesime, parallele al piano medio e sottoposte a tensione piana, eliminando ogni tipo di continuità tra le differenti sezioni orizzontali. A seguito si applicano i carichi, pesati tra gli strati, analizzando l'andamento delle distribuzioni di tensioni e di deformazioni, sommando questi contributi una volta ripristinata la continuità di materiale e di spostamenti. Un metodo simile prevederebbe che il coefficiente di Poisson fosse tale da eliminare la compatibilità cinematica, traforando ogni cubetto in una molla indipendente dall'intorno.Aver supposto gli strati di spessore infinitesimo prevede che questi siano infinitamente rigidi nella direzione di studio, dalla quale ne conviene siano previste deformazioni nulle rispetto alla normale al piano medio, tanto che ricomponendo la piastra si ottiene una deformazione $\varepsilon_z$ nulla, che muove in favore dell'ipotesi di Kirchhoff. Partendo dal principio che le sezioni siano in tensione piana e la piastra non sia comunque un grande spessore, è ragionevole pensare che le tensioni rimangano nulle pure lungo tutto lo spessore di quest'ultima.

Assunte le ipotesi di tensione piana, si può passare ora a definire il vettore delle deformazioni (ε) entro piano, attraverso il legame costitutivo proprio della tensione piana applicata ad un materiale isotropo(casistica che sarà altamente improbabile incontrare nella vita reale).

$\underline{\sigma} = \underline{\underline{D}} \cdot \underline {\varepsilon} = \underline{\underline{D}} \cdot \underline {\varepsilon_0} + \underline {z} \cdot \underline{\underline{D}} \cdot \underline {k}$

$$\begin{bmatrix} \sigma_x \\ \sigma_y \\ \tau_{xy}\\ \end{bmatrix} = \frac {E}{1-{\nu}^{2}} \cdot \begin{bmatrix} \ 1 && \nu && 0 \\ \ \nu && 1 && 0 \\ \ 0 && 0 && \frac {1- \nu}{2} \\ \end{bmatrix} \begin{bmatrix} \ \varepsilon_x \\ \ \varepsilon_y \\ \ \gamma_{xy} \\ \end{bmatrix}$$

$$ \underline{\underline {D}} = \frac {E}{1-{\nu}^{2}} \cdot \begin{bmatrix} \ 1 && \nu && 0 \\ \ \nu && 1 && 0 \\ \ 0 && 0 && \frac {1- \nu}{2} \\ \end{bmatrix} $$

Il modulo di elasticità (E) ed il coefficiente di Poisson ($\nu$) generalmente variano con le caratteristiche del materiale, eccezion fatta nel caso in cui la piastra non sia omogenea, ragion per cui $\nu$ risulta essere funzione anche di z. Infatti nel caso in cui il materiale sia omogeneo lungo lo spessore, allora anche le tensioni saranno omogenee lungo lo spessore.
In analogia con la teoria della trave si ipotizza uno stato monoassiale di tensione, ma non di deformazione, tale che in fase sperimentale si vedrebbe, sottoponendo un provino a trazione, una deformazione entro piano.
Da notare che, quando la matrice D è funzione di z, σ può variare a caso lungo lo spessore, al contrario a fronte di deformazioni lineari varianti ci si troverà in tensione piana.

Per la teoria della trave, quando si vuole passare al calcolo dei momenti, si integrano le σ e le $\tau$ con braccio sull'area in esame, mentre nella piastra, analogamente, per determinare i momenti si integrano le stesse componenti di sforzo, ma non più sull'area, bensì sullo spessore.
Procedendo con il calcolo delle condizioni di sollecitazione (momento flettente e momento torcente) si può definire:

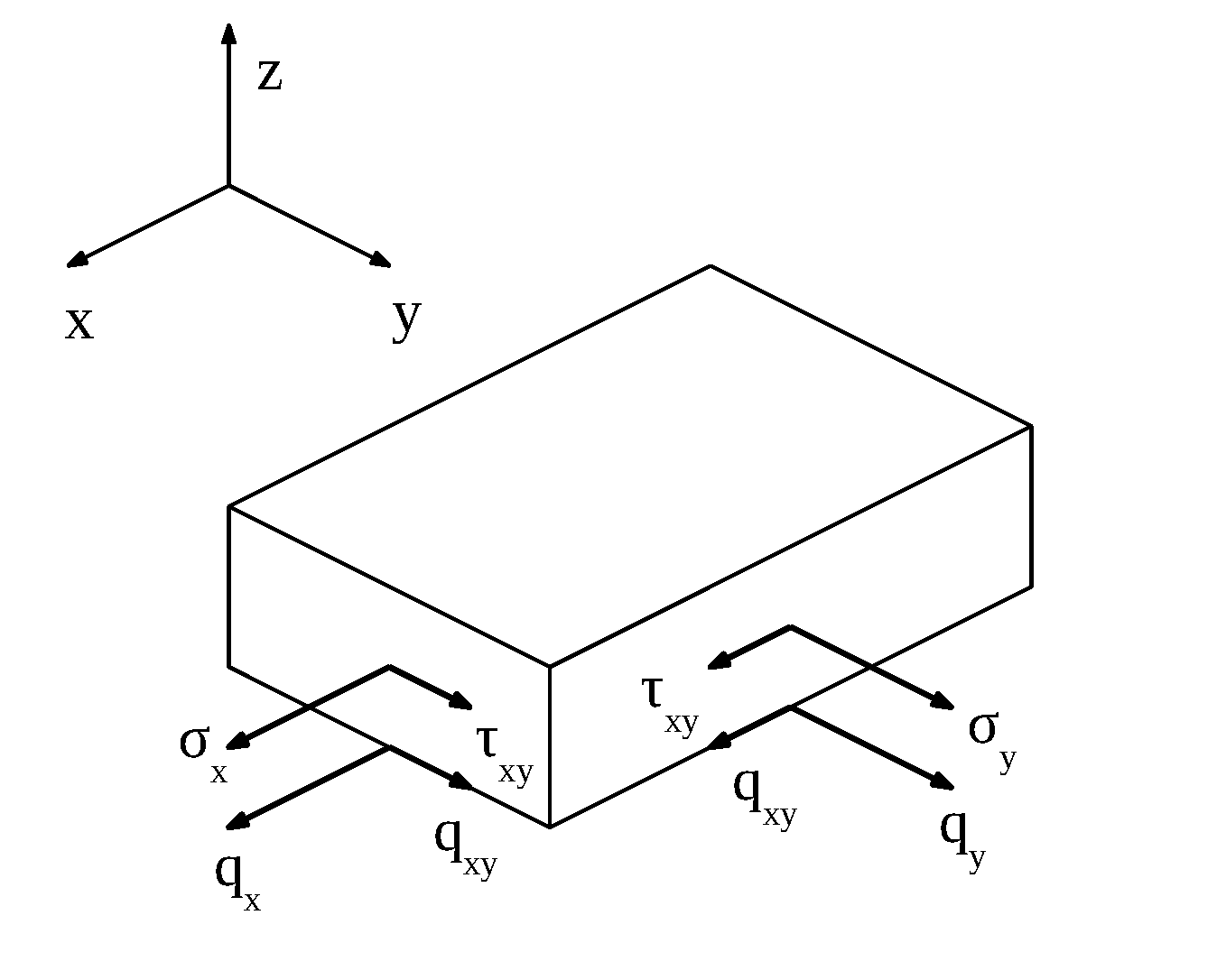
$$\underline {q} = \begin{bmatrix} \ q_x\\ \ q_y \\ \ q_{xy}\\ \end {bmatrix} = \begin{bmatrix} \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_x \mathrm{d}z \\ \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_y \mathrm{d}z \\ \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \tau_{xy} \mathrm{d}z \\ \end{bmatrix} \begin{bmatrix} \ \frac{N}{mm} \\ \end{bmatrix}$$

con q_i è prodotto da $\sigma_i$, mentre q_ij da $\tau_{ij}$.
Quando il piano medio coincide con il piano di riferimento l'integrazione è applicata agli estremi visti,ovvero da -h/2 ad h/2, ma nel caso in cui questa coincidenza tra piani non suscita è necessario introdurre agli estremi di integrazione una quantità s, relativa allo scostamento di un piano rispetto all'altro, così da ottenere un'integrazione da -h/2+s ad h/2+s. Lo scostamento s, anche definito Offset, è notevolmente importante poiché ci aiuta nella moderazione al CAD, a capire in quale direzione si sviluppa la mesh, soprattutto nei casi in cui la geometria non ci viene in supporto.
Il termine $q_x$ idealmente sta ad indicare la forza in direzione x che viene trasmessa per tenere chiusa una cricca indicativa, quest'ultima utile per determinare l'unita di misura della forza [N/mm]. Infatti si potrebbe pensare di determinare le grandezze caratteristiche di $q_x$ tagliando tutto lo spessore, come se avessimo una cricca che si propaga per l'intera estensione, dal piano superiore a quello inferiore.
Quando invece si passa allo studio delle \tau, ci vanno ad analizzare il taglio effettuato lungo il blocchetto, considerando la risultante delle forze y in direzione normale ad x e la risultante delle forze in x lungo la normale alla direzione y. Quanto visto fino ad ora va a rappresentare le sollecitazioni di tipo MEMBRANALE, equivalenti dello sforzo normale e del taglio nello studio di una trave.
Nell'integrazione però si può procedere anche inserendo in tutti i termini il braccio d'azione della forza, in modo da ottenere:

$$\underline {m} = \begin{bmatrix} \ m_x\\ \ m_y \\ \ m_{xy}\\ \end {bmatrix} = \begin{bmatrix} \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_x \cdot z \mathrm{d}z \\ \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_y \cdot z \mathrm{d}z \\ \ \int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \tau_{xy} \cdot z \mathrm{d}z \\ \end{bmatrix} \begin{bmatrix} \ \frac{N mm}{mm} \\ \end{bmatrix}$$

dove m_i è il momento agente sulla faccia perpendicolare all’asse i ed m_ij è generato da $\tau_{ij}$.
Le prime due componenti calcolate indicano i momenti flesso-torsionali relativi ad unità di lunghezza di elemento di trave, mentre l'ultimo il momento torsionale, che si potrà definire nullo qualora le \tau variassero lungo lo spessore. Infatti tagliando lungo lo spigolo si dovrebbe trovare continuità degli sforzi taglianti, ancor più visibile nel momento in cui si discretizzasse l'elemento in tanti cubetti.