La rigidezza di struttura in parete sottile varia in maniera prevedibile rispetto alla variazione di spessore, essa è proporzionale allo spessore se il corpo lavora prevalentemente in modalità membranele o proporzionale al cubo dello spessore se lavora prevalentemente in modalità flessionale.

Prendiamo in esame due profilati in alluminio a sezione quadra di lato 80mm, lunghezza 660mm, giuntati per saldatura e sollecitati da rotazione imposta di 0.1 radianti ad un'estremità e vincolati con un incastro in un'altra come in figura. Sono state modellate sei strutture con sezione che varia da 16 mm a 0.5 mm (spessore decrescente verso destra in figura).

Analizzando la coppia in direzione z dovuta al vincolo di rotazione imposta possiamo determinare la rigidezza della struttura come coppia diviso rotazione imposta.
Una volta lanciato il calcolo è possibile fare considerarioni sulla modalità, membranale o flessionale, in cui lavorano le diverse parti della struttura.

La coppia che agisce in direzione z sollecita il profilato verticale a flessione mentre l'altro a torsione; le pareti dei profilati lavorano prevalentemente in modalità membranale in quanto una trave soggetta a flessione, lontano dai giunti, ci si aspetta che abbia solamente uno stato tensionale monoassiale così come a torsione l'andamento delle tau è uniforme sullo spessore. Quindi, se la deformabilità è dovuta da uno stato tensionale membranale, la rigidezza dovrebbe variare linearmente con lo spessore.
Nell'intorno del giunto però lo stato tensionle è flessionale, come si può vedere nella figura soprastante dove è rappresentata la rotazione z. Si osserva che nell'oggetto a sezione più sottile il profilato verticale, soggetto a flessione, si deforma con rotazione uniforme in tutta la sua lunghezza mentre gran parte del profilato soggetto a torsione si muove con una rotazione quasi nulla, come se i due elementi fossero soggetti ad una rototraslazione nello spazio. In particolare, tutta la deformazione è concentrata al giunto dove le pareti si deformano con grossi spostamenti fuoripiano, ovvero in modalità flessionale.
L'elemento più spesso, invece, ha una rotazione che scala lungo i due profilati tipica di una trave a momento flettente imposto e nell'intorno del giunto non vi sono deformazioni particolari ma vi è continuità fra le rotazioni dei due frofilati.
Nel modello a sezione più elevata è presente una deformabilità nulla al giunto e la deformabilità è distribuita sulle travi secondo il modello di trave a momento flettente e trave a momento torcente. Il modello a spessore meno elevato presenta travi che sostanzialmente rototraslano nello spazio e tutta la deformabilità è associata al giunto. le strutture intermedie si comportano in maniera intermedia.

A questo punto analizziamo il valore della coppia associata alla rotazione imposta in ogni modello plottando il reaction moment z in forma numerica e valutandolo nel punto di applicazione della rotazione imposta. Valutando il valore della coppia in relazione allo spostamento imposto avremo un valore della rigidezza della struttura.

Creiamo un foglio di calcolo dove inseriamo i valori della coppia e calcoliamo le rigidezze, con i dati presi dal modello fem e secondo la teoria della trave.

E' interessante notare il rapporto tra le due rigidezze al variare dello spessore; nel modello a sezione più elevata, quando non è presente una elevata deformazione al giunto, la rigidezza calcolata a fem è l'84% di quella calcolata in teoria della trave mentre nel caso di spessore minore è il 4%. Possiamo affermare quindi che la teoria della trave sovrastima moltissimo la rigidezza della struttura quanto più è presente deformazione al giunto.

Creiamo un grafico bilogaritmico rappresentante la rigidezza in funzione dello spessore.

Dal grafico si nota che la pendenza della linea non è uniforme; vado quindi a valutare il rapporto incrementale in ognuno dei punti di campionamento, ciascuno dei quali rappresenta uno dei sei modelli.
I valori dei rapporti incrementali sono riportati nel foglio di calcolo soprastante e si può notare che variano da 1.18 a 2.69 rispettivamente per la struttura a spessore maggiore e quella a spessore minore.
La teoria prevede che il rapporto incrementale possa variare fra 1 e 3 a seconda di quanto siano dominanti i fenomeni membranali rispetto a quelli flessionali.

giunto_l_rigidezza_spessore_modellimultipli.mud (sono richiesti 2 Gb di ram liberi per il calcolo)
giunto_l_rigidezza_spessore.ods

Fino ad ora sono stati affrontati problemi statici, in cui le sollecitazioni non variano in funzione del tempo. È possibile definire anche sistemi quasi-statici, nei quali la sollecitazione varia in una sequenza temporale ma in evoluzione quasi statica, ossia il tempo non influenza veramente le quantità di interesse del sistema. Da un punto di vista matematico ciò equivale all’assenza nel problema delle derivate rispetto al tempo. I sistemi statici hanno una risposta elastica che è completamente descritta dalla matrice di rigidezza mentre nell’analisi di sistemi dinamici occorre considerare anche la presenza di fenomeni viscosi e inerziali.

Partiamo dalla definizione di matrice di massa di un elemento finito facendo riferimento, come esempio, all’elemento piastra alla Mindlin. In particolare mettiamo a confronto l’elemento 75 piastra 4 nodi con un volumetto di materiale che, tramite la sola combinazione di elementi hex8 e link cinematici, replica il comportamento della piastra a lui sopra e rispetto al quale sarà definita la matrice massa.

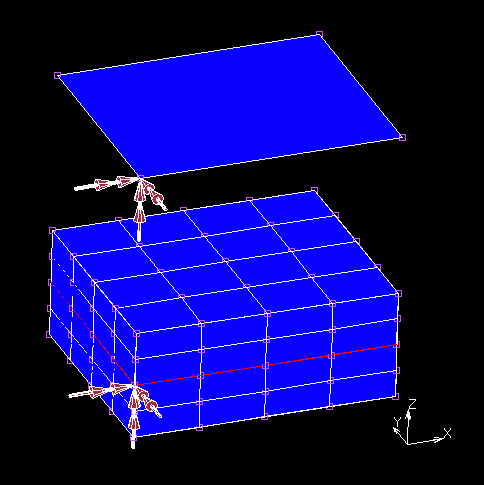
Per implementare la cinematica della piastra alla Mindlin sui 25 nodi giacenti sul piano medio, preso come piano di riferimento, è stato costruito un vincolo di corpo rigido che percorre tutto lo spessore, dall’estremo inferiore a quello superiore, in questo modo tutto il materiale appartenente ad un segmento verticale continua a rimanere su di esso anche una volta deformato ed inoltre rototrasla rigidamente. Per rendere gli spostamenti e le rotazioni interpolate in maniera bilineare lungo il piano medio sono stati imposti opportuni servolink tra i nodi adiacenti a quello centrale e il nodo centrale stesso. Una volta costruito il modello è possibile vedere come si deforma effettivamente il materiale dell’elemento 75 quando gli applico degli spostamenti elementari ai nodi. Consideriamo il volume infinitesimo dell’elemento dΩ , un sistema di coordinate globali xyz e un sistema di coordinate locali $\xi\eta\zeta$, che può anche coincidere con quello globale. Ogni nodo ha 6 gradi di libertà: $u _{i}$,$v _{i}$,$w_{i}$,$\varphi _{xi}$,$\varphi _{yi}$,$\varphi_{zi}$. Avendo 4 nodi, ho un totale di 24 gdl. Andiamo ad imporre ad ogni nodo il suo moto elementare associato allo specifico gdl; ciò corrisponde a fissare un valore unitario di un singolo gdl per un determinato nodo e imporre nulli tutti i rimanenti gdl. Ognuno di questi moti elementari definisce una specifica deformata. Imponiamo ad esempio sul primo nodo del nostro elemento piastra una rotazione unitaria attorno l'asse y, mentre nei restanti tre nodi sono posti nulli gli spostamenti e le rotazioni. La deformata del moto elementare del grado di libertà rotazione attorno l’asse y è la seguente:

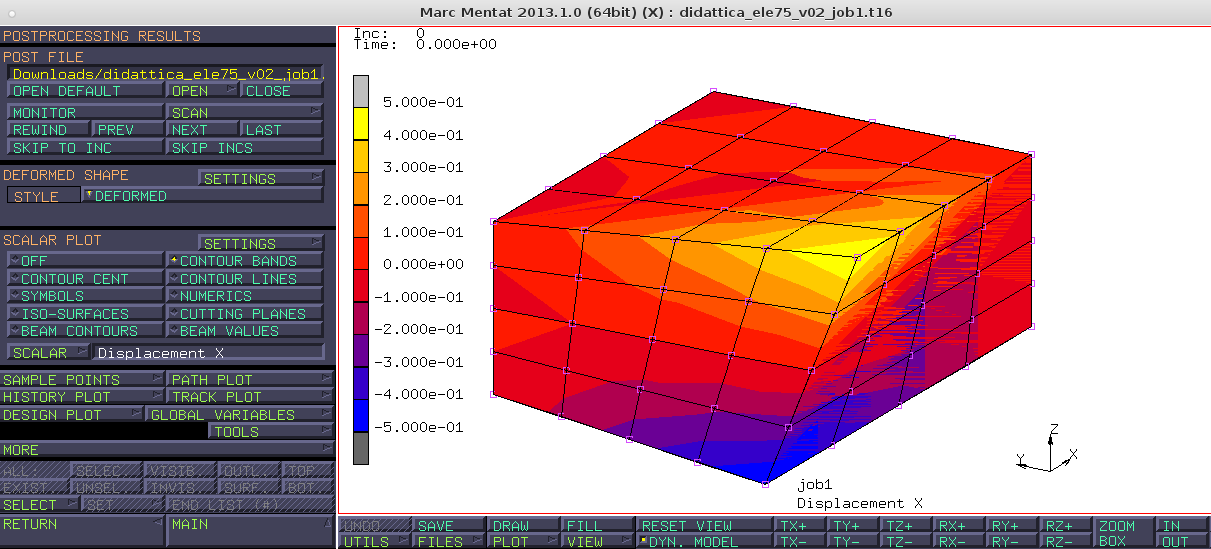
Nella figura si può vedere il campo di spostamento generato in direzione x, che può essere raccolto in una funzione scalare $N_{j}^{u} (\xi ,\eta ,\zeta)$ nelle coordinate locali $\xi$, $\eta$, $\zeta$, dove u indica lo spostamento lungo x e j lo specifico grado di libertà. Applicando il medesimo procedimento anche ai moti elementari di spostamento lungo y e z si ottengono le funzioni $N_{j}^{v} (\xi ,\eta ,\zeta)$ e $N_{j}^{w} (\xi ,\eta ,\zeta)$. Per ciascun grado di libertà si può quindi costruire il vettore

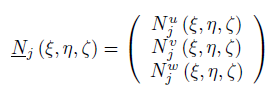
La natura di tali $\underline{N}_{j} (\xi ,\eta ,\zeta )$ è propria dello specifico elemento; ad esempio per un elemento isoparametrico piano 4 nodi, con nodi numerati (1,2,3,4) si ha:

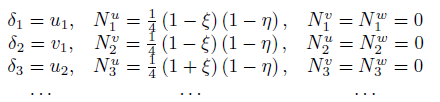
Il campo degli spostamenti $\underline{\delta ^{*}}$ è rappresentabile nella forma 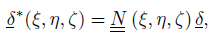dove

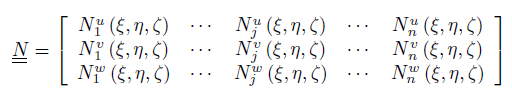
È una matrice 3 x n, con n numero gradi di libertà nodali totali sull’elemento e 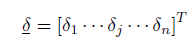è il vettore contenente tali gdl. Poiché la matrice dei moti elementari non è funzione del tempo, derivando il campo degli spostamenti $\underline{\delta ^{*}}$ si ottiene il campo di velocità: 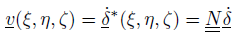L’energia cinetica propria del materiale compreso entro l’elemento vale 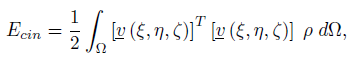dove ρ è la densità puntuale del materiale. Sostituendo al suo interno la forma generica della velocità puntuale, si ottiene 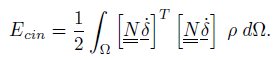ricordando infine che il vettore delle velocità nodali non varia nelle variabili di integrazione, si ottiene la forma finale 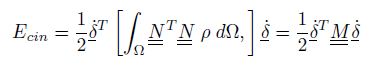da cui si ricava la definizione di MATRICE DI MASSA $\underline{\underline{M}}$. L’integrazione di quest’ultima formula può essere condotta per quadratura gaussiana; in particolare si può scrivere 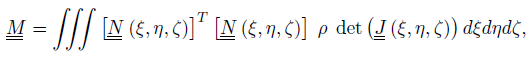Dove $\underline{\underline{J}}(\xi ,\eta ,\zeta )$ è lo Jacobiano relativo al cambio di coordinate (ξ,η,ζ) → (x,y,z). Eguagliando la variazione nel tempo di energia cinetica 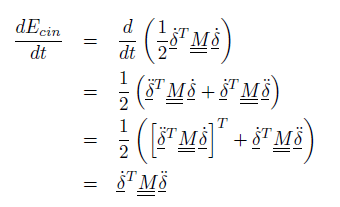alla potenza fornita da un sistema di forze esterne agenti sui nodi dell’elemento (tali forze equilibrano sul nodo le reazioni inerziali, e quindi sono ad esse uguali e contrarie) 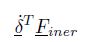otteniamo la relazione: 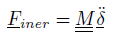che lega le forze da applicare all’elemento affinché questo acceleri con determinate accelerazioni nodali (derivate seconde nel tempo degli spostamenti ai vari gdl). $\underline{\underline{M}}$ è una matrice simmetrica e definita positiva, ciò comporta che qualunque vettore velocità non nullo deve dare un contributo di energia cinetica esclusivamente positiva. La matrice delle rigidezze $\underline{\underline{K}}$ è invece semidefinita positiva; esistono spostamenti non nulli che generano energia potenziale elastica nulla, questi sono i moti di corpo rigido.

Si definisce equilibrio dinamico per una struttura elastica, massiva e con possibilità di dissipazione di tipo strutturale o viscosa la seguente equazione:

$$M\ddot{x} + C\dot{x} + Kx = F(x)$$

dove x=x(t) è la risposta nel tempo del sistema, ovvero il vettore dei gradi di libertà del sistema.

• $M\ddot{x}$ sono le forze esterne da applicare alla struttura per avere l'accelerazione $\ddot{x}$
• $C\dot{x}$ sono le forze esterne da applicare alla struttura per mantenere la velocità $\dot{x}$ in presenza di dissipazioni.
• $Kx$ sono le forze esterne da applicare alla struttura perequilibrare le reazioni elastiche date dagli spostamenti $x$.

Se le forze esterne $F(t)$ sono pari alla somma di questi tre contributi allora si ha l'equilibrio dinamico.

Ricerchiamo ora la soluzione peridica del problema, cioè la risposta a regime a sollecitazioni periodiche, trascurando quindi il transitorio. Per fare ciò si può scomporre la forzante in somma di armoniche utilizzando la serie di Fourier: $$F(t)=\bar{f}e^{j\omega t}$$ Se il problema è lineare possiamo valutare la risposta del sistema ai singoli contributi e ricomporre le varie risposte per ottenere la risposta globale.
$\bar{f}$ è un vettore complesso che ha per elementi modulo e fase di ogni grado di libertà del sistema.
Un sistema lineare da una risposta armonica a fronte di una sollecitazione armonica. Un sistema può diventare non lineare a causa di plasticità, attriti o contatto monolatero. Per fare un esempio pratico consideriamo un righello appoggiato su una scrivania e vincolato ad essa solo attraverso uno spigolo, se viene sollecitato la sua risposta può essere considerata armonica: Se invece lo stesso righello è per metà appoggiato alla scrivania e per metà libero allora nel moto di salita sarà libero mentre nella fase di discesa avrà un contatto monolatero con la scrivania. Quindi varia la configurazione della matrice di sistema durante il moto e di conseguenza il problema non sarà più lineare. Nella pratica ingegneristica si trattano come lineari anche sistemi non lineari, commettendo un certo errore, ma evitando un aumento eccessivo del costo computazionale. Dall'analisi dei sistemi lineari si ottiene il seguente sistema $$(-\omega M+j\omega C+K)\bar{x}=\bar{f}$$ sistema di n equazioni in n incognite complesse. Si nota che per $\omega\rightarrow0$ il problema si riconduce a un caso statico, per $\omega \rightarrow \infty$ il sistema diventa analogo alla legge di Newton $F=ma$.

Si vanno a ricercare i modi propri della struttura, ossia quei particolari moti periodici che sono ammessi dall'equazione di equilibrio dinamico, anche in assenza di forzante applicata. Per garantire periodicità devo eliminare il termine dissipativo, ciò può essere fatto ponendo $C=0$ o più “finemente” utilizzando un elemento dissipativo il cui moto è legato a quel modo proprio del sistema, cioè durante l'oscillazione non si muove e di conseguenza non dissipa energia. Per esempio se consideriamo il primo modo di vibrare del diapason, lo smoraztore posto in posizione come in figura 1 non dissipa energia durante l'oscillazione, mentre dissipa energia se consideriamo il modo 2 (figura 2).

Eliminando il termine dissipativo si ottiene il sistema algebrico nell'incognita $\omega^2$ $$(-\omega^2 M+K)\bar{x}=0$$ dove il termine moltiplicativo di $\bar{x}$ viene chiamato matrice di sistema. Si tratta di un problema agli autovalori le cui soluzioni sono le coppie autovalore e autovettore $(\omega _{i}^2,\bar{x}_{i})$. Essendo $M$ definita positiva si può riscrivere come: $$(M^{-1}K-\omega^2I)\bar{x}=0$$ I valori di $\omega^2$ che forniscono soluzioni non banali del problema sono le radici del polinomio: $$det(K-\omega^2_{i}M)=0$$ da cui si ricavano lecoppie di autovalori e autovattori $(\omega _{i}^2,\bar{x})$ che rappresentano la pulsazione e la forma del moto proprio i-esimo. Se non si vuole calcolare l'inversa della matrice di massa ${M}^{-1}$ per ridurre il costo comutazionale, si può ricorrere al problema agli autovalori generalizzato in cui la matrice che moltiplica $\omega^2$ non è una matrice identità $I$. Si tratta di trovare i valori di $\lambda,v$ tali per cui $$Av-Bv=0$$ e quindi $$(K-\omega^2IM)\bar{x}=0$$

Gli autovettori sono definiti a meno di una costante se gli autovalori sono tutti distinti, quindi se $\bar{x}_i$ è un modo proprio lo è anche $\lambda\bar{x}_i$. Se gliautovalori non sono tutti distinti, per esempio esiste un autovlore $\lambda$ (con molteplicità 3) a cui sono associati tre autovettori, questi possono essere combinati linearmente a formare un quarto autovettore e quindi formano un sottospazio. Di consegueanza ogni base di quel sottospazio è una terna di autovettori per cui anche per pulsazioni nulle si possono trovare modi propri di vibrare.
Gli autovettori ricavati dal problema sono normalizzati secondo la normalizzazione a massa modale che prevede la scalatura della massa modale in modo che il suo valore sia unitario. $$\bar{x}^T_iM\bar{x}_i=\lambda\bar{x}^T_iM\lambda\bar{x}_i=1$$ dove $\bar{x}^T_iM\bar{x}_i$ è la massa modale.

Di conseguenza i risultati ricavati dall'analisi FEM non sono da considerare in valore assoluto, ma sono da scalare in segno e in modulo. Si può invece valutarli in senso relativo, per esempio se consideriamo lo stato tensionale, esso avrà una determinata distribuzione per ogni moodo proprio, di conseguenza in base al punto in cui si ha rottura si può capire quale modo proprio l'ha provocata.