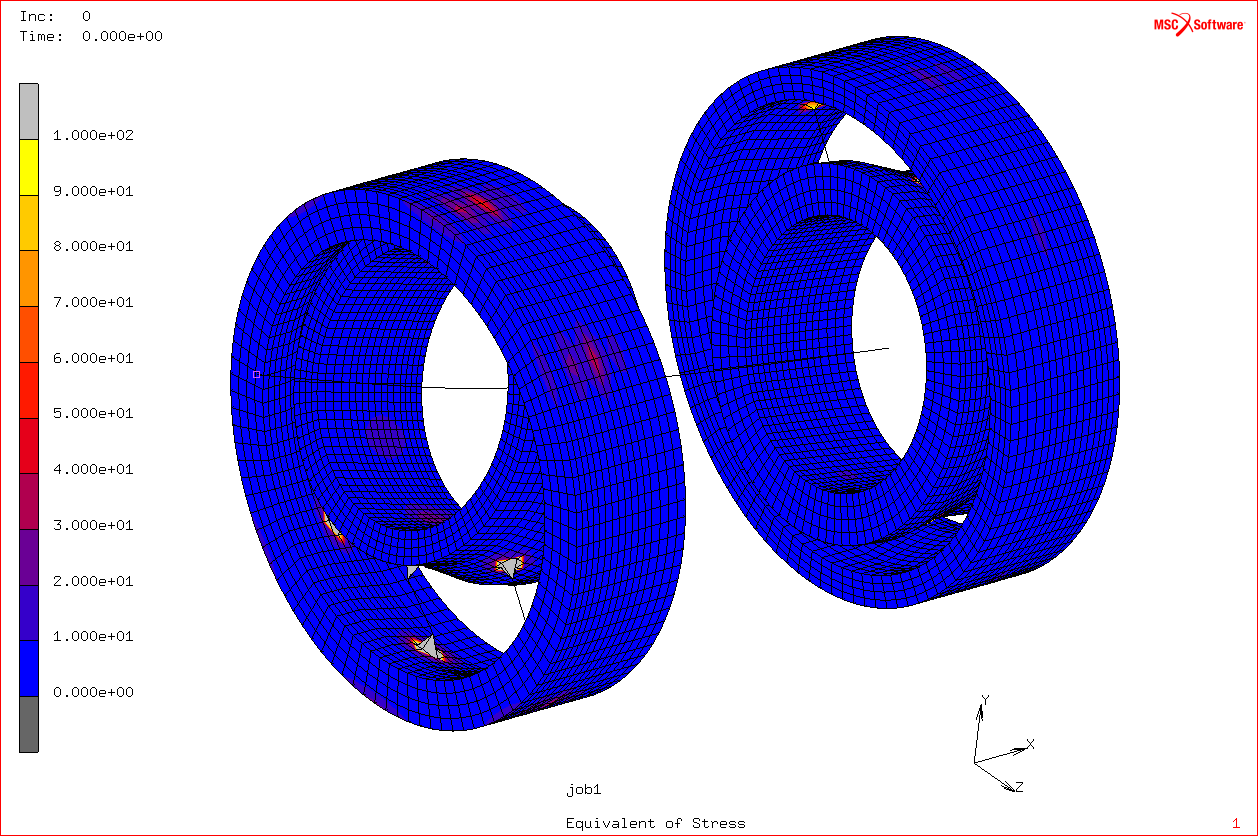Ipotizziamo una sollecitazione su una lamella; applichiamo una forza concentrata, funzione del tempo, F(t)=F*cos(ωt), in un vertice della lamella. Invertire il verso della forza implica un'inversione di fase di 180 gradi.

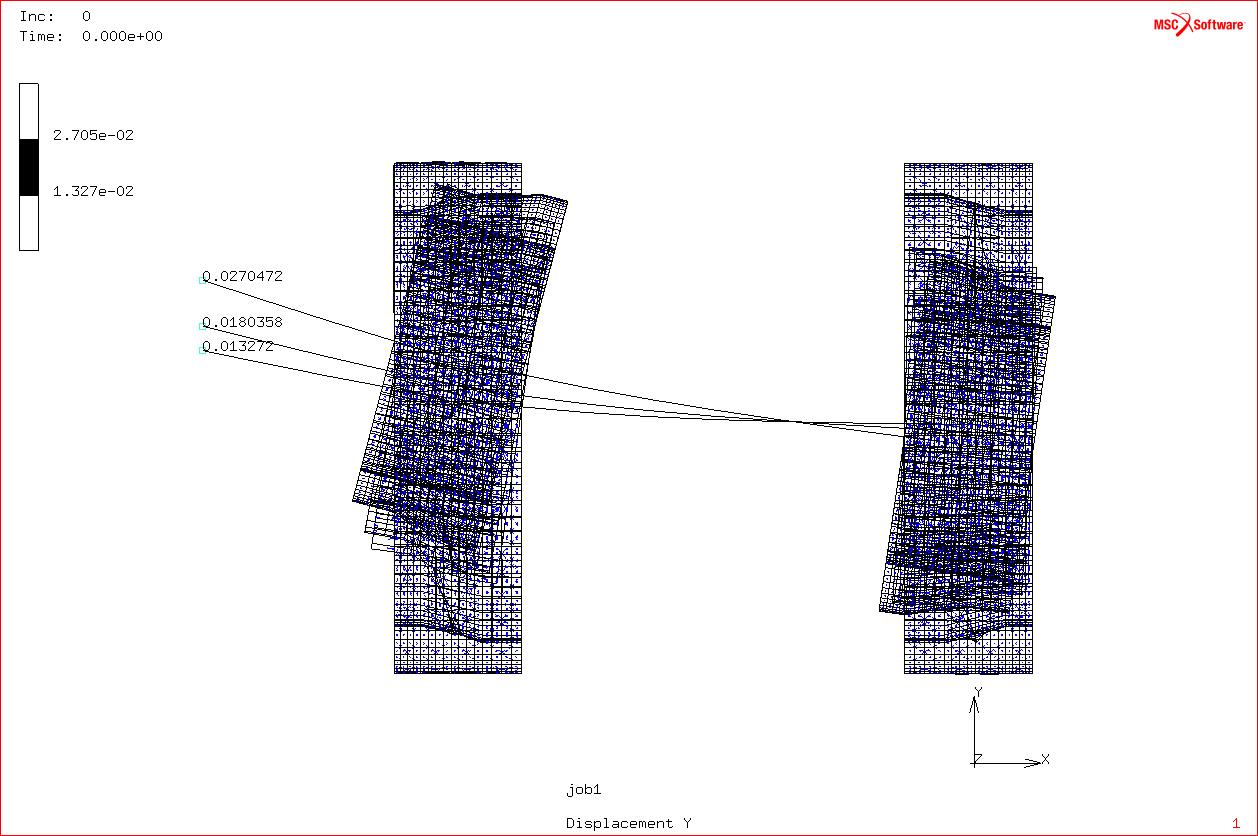
La forza è applicata al vertice per rendere il problema di sollecitazione più semplice possibile. Essendo una sollecitazione armonica, andiamo ad estrarre le risposte in ambiente FEM (analisi del corpo). La cosa che ci interessa è lo spostamento δ, in direzione z, associato ad un modo.

q_i è il termine di accoppiamento modo-forzante. Per una forza unitaria, F=1÷1.5N, ed in base ai modi x₁, x₂ ed x₃ (ai quali vengono associate, rispettivamente, le frequenze 29.02 Hz, 182.2 Hz e 233.8 Hz) si hanno i seguenti risultati:

Lo smorzamento frazionale critico vale l'1% per tutti.
Dai risultati in ambiente FEM si nota come un modo proprio antisimmetrico con una sollecitazione simmetrica, su una struttura simmetrica, annulla la q_i.
Individuando la pulsazione della forzante F ad 80 Hz (valida per tutti i modi), possiamo definire r come il rapporto tra le frequenze (r=frequenza forzante/frequenza propria).

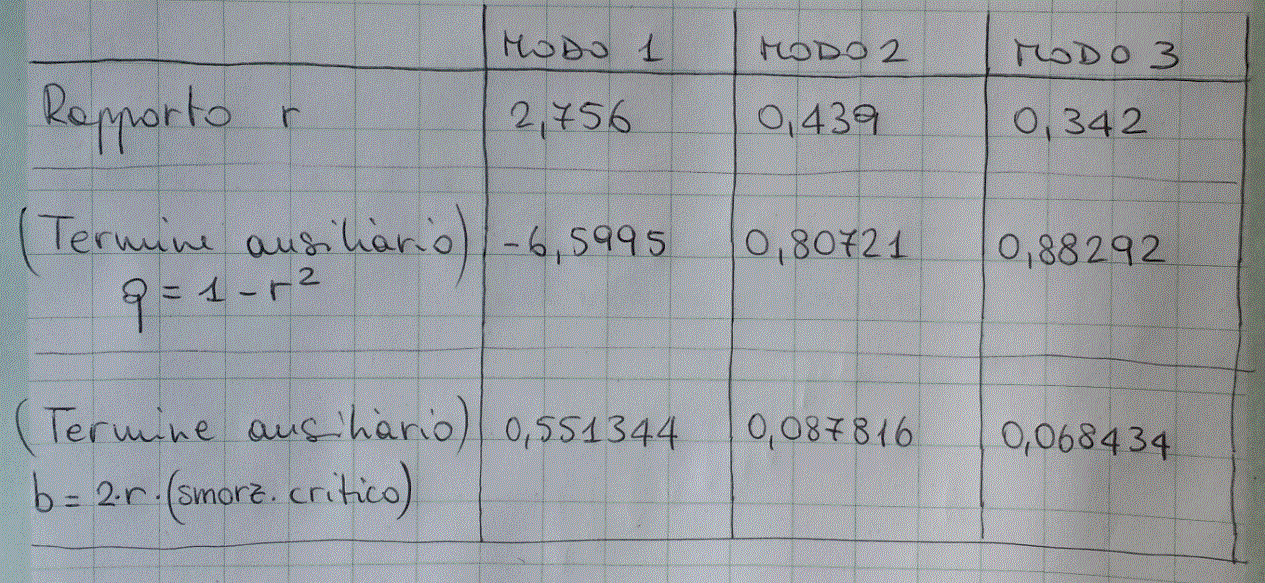
Questi risultati ci permettono di ricavare il termine ξ:
Re(ξ)=inserire formula
Im(ξ)=inserire formula
Analizzando una grandezza di campionamento su risposta (comp 11 stress, layer 1 all'incastro in MPa)
1082.85 -6066.85 0
I contributi di soluzione sono dati da:
comp.11 * Re(ξ) [MPa]
comp.11 * Im(ξ) [MPa]
Il valore complessivo risulta essere:
Re=-3.6350131 MPa
Im=0.007178194 MPa
modulo=3.635020189 MPa
Si nota come, all'avvicinare della frequenza della forzante a quella del primo modo, i valori del sistema crescono.
La teoria dell'elasticità dice che se applico una forza (linea di forza) su un corpo piano elastico, si crea una distribuzione di pressione infinita lungo la linea di forza.

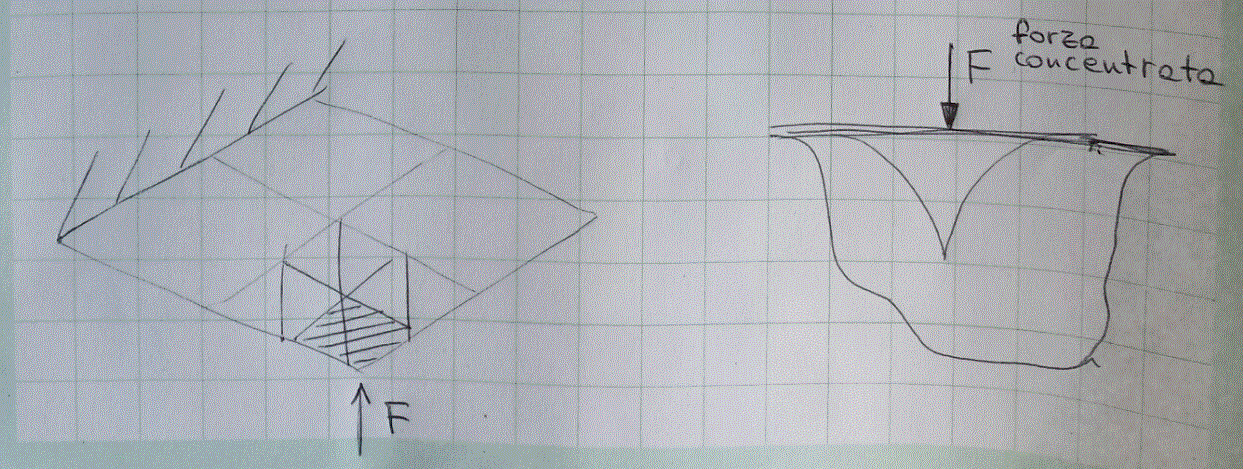
Però, tornando, in ambiente FEM, all'applicazione di una forza F ad un nodo (quello estremo): l'area di influenza sarà 1/4 di quella di partenza. Si nota come la soluzione di spostamento in quel punto, all'infittire della mesh, è infinito (risultato divergente).
Una struttura a piastra non può essere soggetta a carico concentrato perchè crea problemi di spostamenti infiniti.

Danno singolarità finita solo agli spostamenti su corpi 3D. Per le piastre è complicato ma reggono ai carichi di linea. Per le travi, esse supportano benissimo i carichi nodali concentrati e danno singolarità finita agli spostamenti ed alle tensioni.
Sulle piastre, l'applicazione di un carico nodale concentrato va da top a bottom sullo spessore. Se il carico fosse distribuito su una linea, la risultante q*b è spalmata sull'area b*h finita, quindi da singolarità logaritmica agli spostamenti.

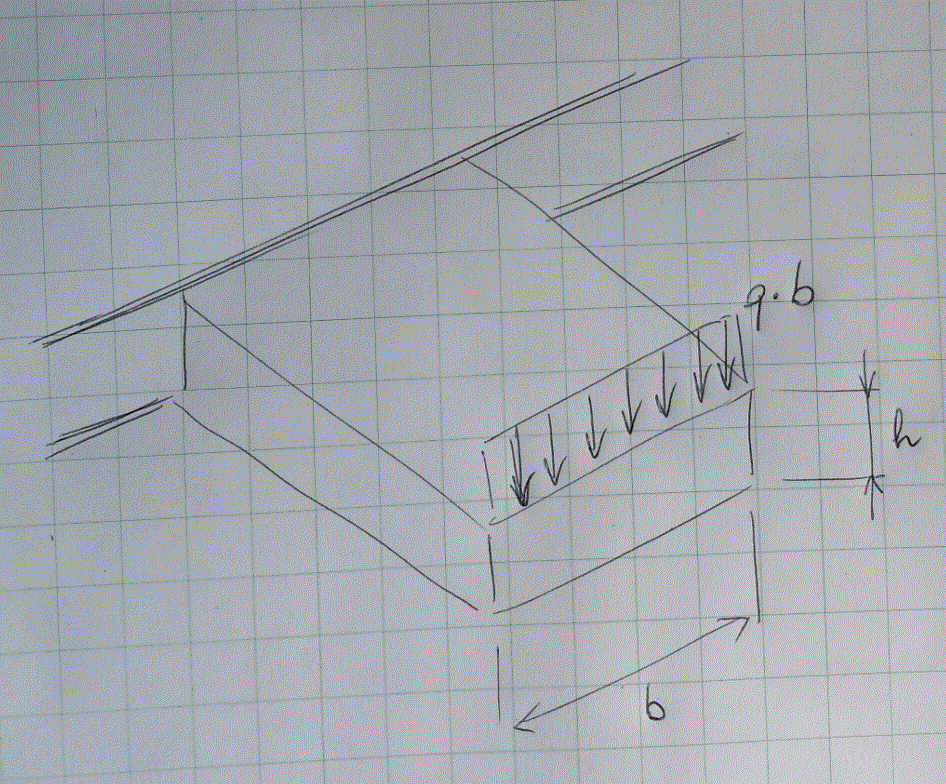
Le piastre alla Kirchhoff non hanno spostamenti singolari legati a forze concentrate poichè le τ sono nulle. La singolarità alle tensioni c'è sempre per le piastre, ho anche singolarità agli spostamenti se la piastra è alla Mindlin. La singolarità dipende dal tipo di piastra.

https://engineering.purdue.edu/~ce573/Documents/Structural%20damping%20values_JDStevenson.pdf

http://iopscience.iop.org/1742-6596/268/1/012022/pdf/1742-6596_268_1_012022.pdf

http://teaching.ust.hk/~mech300/mech300_7_1_damping_ref.pdf

http://www.vibrationdata.com/tutorials/bolted_joint_damping.pdf

modello marc/mentat