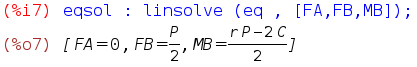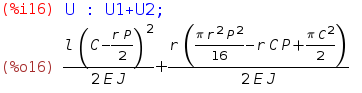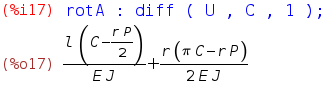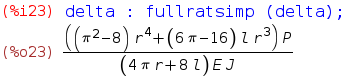Esercizio maglia di catena

maglia di catena, modello cattedra fine lezione ven 26 feb, formato wxm

Si vuole valutare lo stato tensionale di una maglia di catena in trazione mediante la teoria della trave: tale struttura può essere risolta anche col Metodo degli Elementi Finiti, ma con opportune considerazioni risulta più semplice da risolvere come trave.

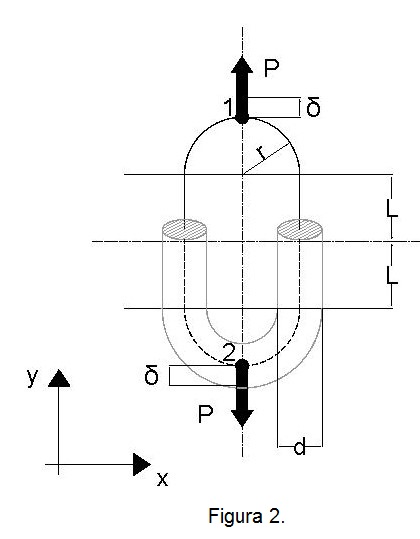
L'asse della maglia può essere pensato composto da due tratti rettilinei, ciascuno di lunghezza 2L, e da due semicirconferenze di raggio r. La sezione è circolare di diametro d.

Sulla maglia agiscono due carichi concentrati di intensità P alle estremità. La struttura presenta carichi ma non vincoli, ciononostante il problema ha senso, in quanto i carichi esterni sono in equilibrio. Per prima cosa si valutano le deformazioni.

Il corpo presenta due piani di simmetria ortogonali al piano x-y, come si nota in figura 2.

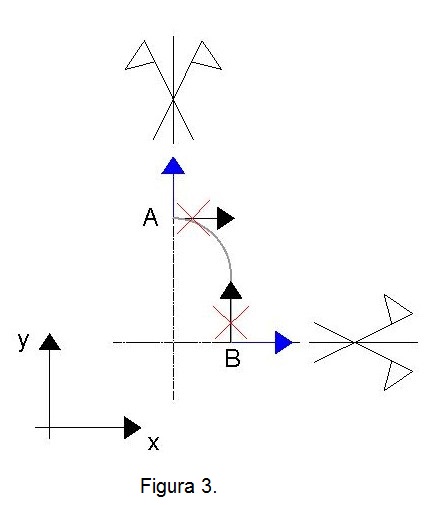
Poiché il sistema risulta simmetrico e caricato simmetricamente, esso si deforma e si tensiona simmetricamente. Per questo motivo è lecito considerare solamente 1/4 di struttura. Per fare ciò, è necessario introdurre vincoli di simmetria che garantiscano la compatibilità cinematica della struttura: si vuole infatti garantire l'assenza di compenetrazione e di distacco di materiale tra la porzione modellata e le restanti. Per ogni piano di simmetria si identificano 3 direzioni: una ortogonale e due parallele. I vincoli di simmetria hanno il compito di bloccare gli spostamenti in direzione normale e le rotazioni entropiano.

$u_{\perp}=0$ $\quad$ $\quad$ $u_{\parallel,1} , u_{\parallel,2}$ liberi

$\theta_{\parallel,1}=\theta_{\parallel,2}=0$ $\quad$ $\quad$ $\theta_{\perp}$ libero

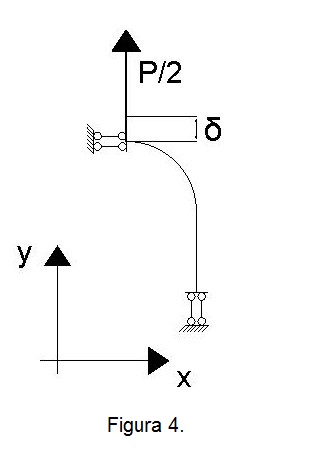
Si noti che nella figura 4 il carico passa da P a P/2 in quanto l’altra metà del carico è applicata nel punto simmetrico ad A.

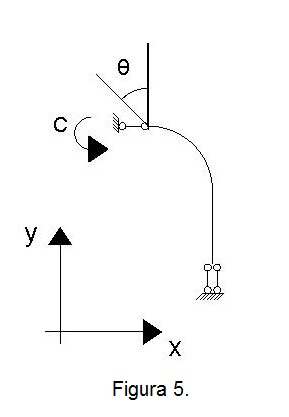
Considerate tali tali condizioni sugli spostamenti, si inseriscono due doppi pendoli. In questo modo la struttura risulta una volta iperstatica. Per renderla isostatica si sostituisce un doppio pendolo con un carrello e si introduce l’incognita iperstatica C legata alla coppia del punto in cui è stato eliminato il vincolo. Per garantire la compatibilità cinematica si pone $$\theta=0$$

A questo punto si può risolvere la struttura mediante il Teorema di Castigliano.

TEOREMA DI CASTIGLIANO

Formula per calcolare l'energia elastica interna di una trave, caso tridimensionale. Si suppone che x,y siano assi principali d'inerzia, e che il momento torcente sia calcolato rispetto al centro di taglio (che coincide con il baricentro nelle sezioni a doppio asse di simmetria).

$$ \def\d{\,\mathrm{d}} U= \int_{l} \frac{M_{f,x}^2}{2 E J_{xx}} + \frac{M_{f,y}^2}{2 E J_{yy}} + \frac{N ^2}{2 E A} +\eta_{x}\frac{T_{ x}^2}{2 G A} +\eta_{y}\frac{T_{ y}^2}{2 G A} + \frac{M_{t }^2}{2 G K_{t}} \d l $$

Utilizzando il Teorema di Castigliano è possibile calcolare l’allungamento totale δ, incognita del problema in esame. Tale teorema vale su ipotesi di sistemi elastici lineari ed enuncia che:

“lo spostamento δ misurato al punto di applicazione della forza P, ha direzione e verso di P e modulo: $$ \delta = \frac{\partial U}{\partial P} $$ “

La coppia C genera una rotazione ϴ della sezione a cui è applicata, calcolabile attraverso il teorema di Castigliano:

“la rotazione di una sezione a cui è applicata una coppia C ha direzione e verso della coppia e modulo: $$ \theta = \frac{\partial U}{\partial C} $$ ”

Essendo questo un problema piano, l'espressione dell' energia potenziale si semplifica e diventa :

$$ \def\d{\,\mathrm{d}} U= \int_{l} \frac{M_{f}^2}{2 E J} + \frac{N ^2}{2 E A} +\eta\frac{T^2}{2 G A} \d l $$

Si introduce l'ipotesi semplificativa di trave sottile: in questo modo si possono trascurare i contributi dello sforzo normale e del taglio rispetto a quello del momento flettente:

$$ \def\d{\,\mathrm{d}} U= \int_{l} \frac{M_{f}^2}{2 E J} \d l $$

Si dovrà in seguito valutare se tale ipotesi è verificata per maglie di catena normalmente utilizzate.

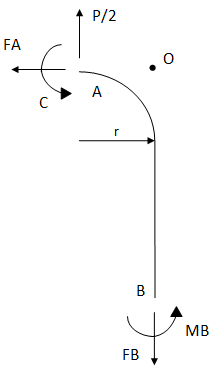
Dalle equazioni di equilibrio alla traslazione verticale ed orizzontale e alla rotazione attorno al punto O si ricavano i valori delle reazioni vincolari in funzione di C e di P/2.

A questo punto risulta semplice ricavare l'espressione del momento flettente e dell'energia elastica della porzione considerata.

Derivando quest'ultima rispetto a C e ponendo l'equazione uguale a 0, si ottiene il valore dell'incognita iperstatica C.

Si può quindi calcolare l'energia elastica dell'intera maglia, derivarla rispetto a P e ricavare lo spostamento 2δ.

1 Pulizia della memoria

Prima di iniziare un nuovo lavoro, è consigliabile pulire la memoria con il seguente comando:

2 Equilibrio

Per assegnare il nome “pippo” all'espressione “pluto” si scrive:

Si definiscono eqtx, eqty, eqr0 le equazioni di equilibrio rispettivamente alla traslazione orizzontale, verticale e alla rotazione attorno al punto O:

Si crea una lista, di nome eq, che comprende il set di equazioni:

Analogamente si sarebbe potuto sfruttare il comando “%”, che richiama la riga precedente, per assegnare un nome alla lista:

Mediante “linsolve( lista equazioni , lista variabili )”, si risolve il sistema lineare nelle incognite assegnate. Il comando restituisce la lista delle variabili ottenute sotto forma di ipotesi:

I risultati ottenuti con “linsolve” non vengono direttamente sostituiti alle variabili incognite. La valutazione esplicita con il comando “ev( variabile )” fornisce il risultato ottenuto dalla risoluzione del sistema solamente sotto una lista di ipotesi. In questo modo si possono impostare una serie di ipotesi e decidere di volta in volta quale utilizzare, oppure risolvere lo stesso problema sotto ipotesi diverse. La sostituzione non è definitiva.

Si può assegnare ad una lista di variabili la loro valutazione sotto certe ipotesi, e in questo caso la sostituzione è definitiva:

In alternativa si possono sostituire automaticamente tutti i risultati nelle rispettive variabili con il comando “globalsolve=true”:

3 Momento Flettente

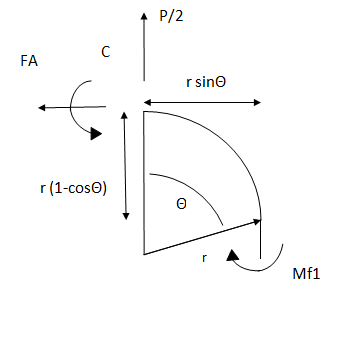
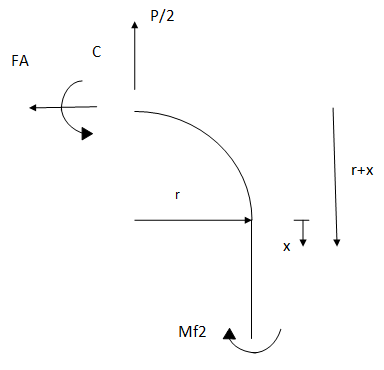
Si calcola il momento flettente del quarto di maglia come somma dei momenti flettenti relativi al tratto rettilineo (1) e al tratto curvo (2):

NB:Nel disegno sopra a sinistra l'origine della quota radiale $r$ deve coincidere con il centro dell'arco di circonferenza; il segmento verticale al quale sembra essere applicato Mf1 è un refuso grafico.

4 Energia potenziale elastica

Si ricava l' espressione dell’ energia potenziale elastica U dei due tratti, utilizzando il comando di integrazione “integrate( funzione ,variabile , valore iniziale , valore finale)”

L'energia elastica della porzione è pari alla somma dell'energia elastica sui due tratti:

5 Rotazione

Utilizzando il teorema di Castigliano, si può calcolare la rotazione θ. Il comando di derivazione è “diff( funzione , variabile , ordine di derivazione )”

6 Equazione di compatibilità

Per l'equazione di compatibilità cinematica si impone la rotazione θ nulla:

7 Coppia

Si risolve l'equazione lineare nell'incognita iperstatica C:

8 Energia potenziale elastica totale e spostamento

Si vuole ricavare la deformazione dell'intera maglia sotto carico P. Per avere un'applicazione standard del teorema di Castigliano si sostituisce uno dei due carichi con un carrello che fornisca una reazione equivalente. L'energia totale del sistema è pari a quattro volte quella del quarto di maglia. Con il comando “infeval” vengono eseguite sostituzioni successive finché l'espressione risulta funzione del minor numero di variabili. Bisogna essere sicuri che non vi siano definizioni ricorsive, poiché in questo caso il sistema può andare in loop. Il comando “fullratsimp(variabile)” esegue una semplificazione dell'espressione riducendo a denominatore comune:

9 Confronto

Definendo il modulo della catena come la distanza tra i punti di contatto maglia-maglia, si può confrontare la deformazione di quest'ultima con la deformazione a trazione di un tondino dello stesso materiale e di pari sezione.

Si introducono le formule di A e J relative alla sezione circolare in esame:

Si definisce il parametro k come il rapporto tra la deformazione della maglia e quella del tondino di riferimento:

Si ottiene una relazione che dipende solamente dai tre parametri l, r e d caratteristici della maglia.