a cura di Alberto Conti

Ci si propone di determinare lo stato tensionale di una lastra infinita con foro finito di raggio unitario, caricata a remoto.

Si procede innanzitutto pulendo la memoria e si stabiliscono le condizioni di caricamento a remoto (far field), imponendo una trazione unitaria lungo x, secondo il sistema di coordinate cartesiane iniziale. dove sxx_ff, syy_ff e sxy_ff indicano le tensioni normali e tangenziale a remoto.

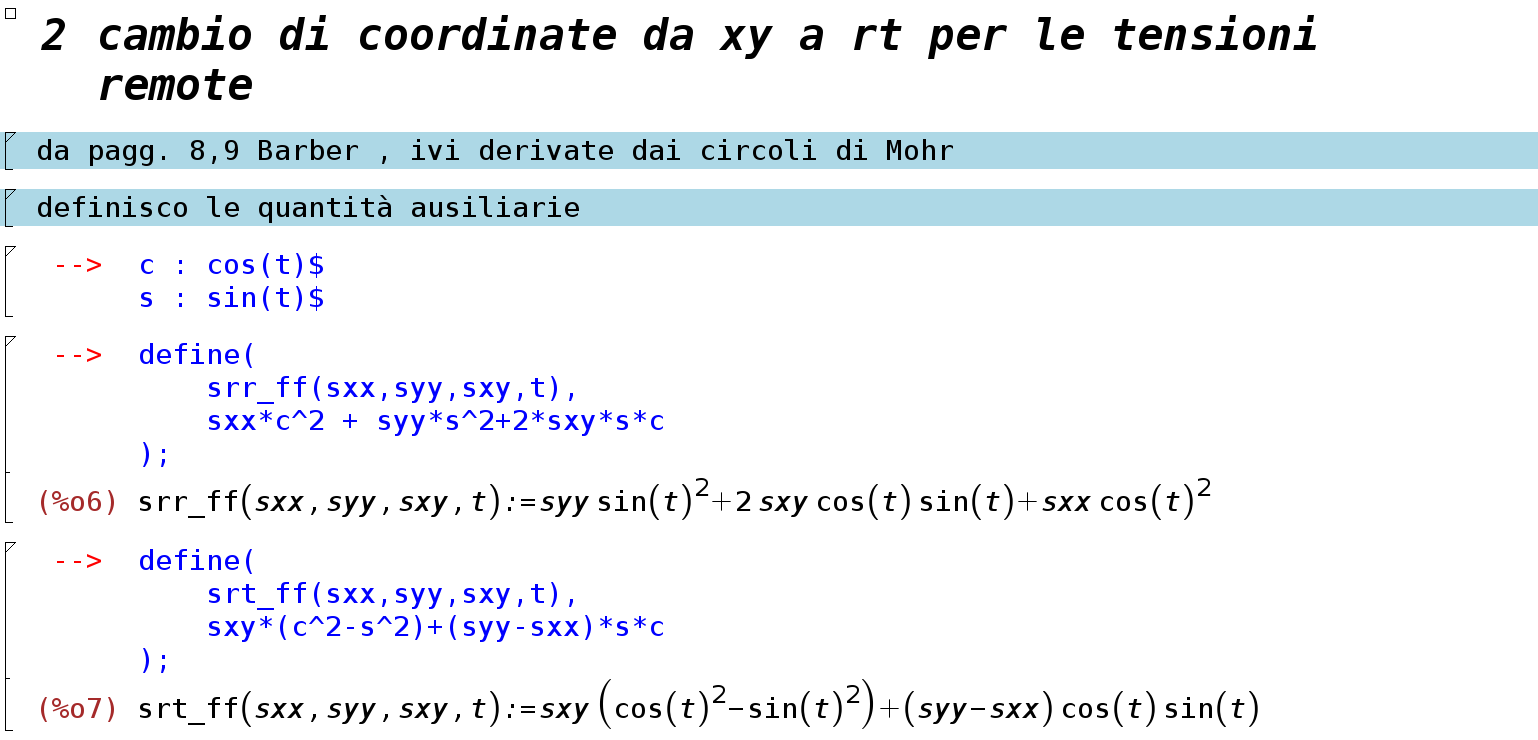
Avendo imposto le condizioni di far field nel sistema di riferimento cartesiano, si opera un cambio di coordinate al fine di esprimere le tensioni in coordinate polari. Le relazioni fra le tensioni nei due sistemi di riferimento sono date dalle espressioni 1.15-1.17, pag. 9 Barber. dove srr_ff è la tensione radiale (σ_{r_ff}), stt_ff quella circonferenziale (σ_{t_ff}) e srt_ff la componente tangenziale (τ_{rt_ff}).

Una volta terminato questo cambio si eliminano le quantità ausiliarie. Come si può notare dalla tabella di pag. 119 del Barber, le componenti tensionali non compaiono in forma cos²(θ) e sen²(θ) ma sono del tipo cos(nθ) e sen(nθ). Si esegue quindi uno sviluppo in serie di Fourier (che risulta in forma esatta essendo applicato a funzioni armoniche), in modo da ottenere funzioni trigonometriche in nθ, da cui risalire al rispettivo termine di Michell. Questa operazione viene eseguita mediante la funzione “trigreduce”:

Si crea ora una lista contenente le appropriate soluzioni di Michell della Airy Stress Function (ricavate dalla tabella di pag. 133 del Barber) ed una lista con i coefficienti incogniti della combinazione lineare:

Per creare quest’ultima lista si è usato il comando “makelist”, che permette di variare automaticamente il numero dei termini incogniti facendo in modo che sia uguale alla lunghezza della lista delle soluzioni di Michell. Il primo elemento da passare al comando è la forma generica del termine con cui la lista viene definita (A[i]); il secondo è l’incognita di scorrimento; il terzo e il quarto sono gli estremi di variazione. Si definisce quindi la Airy Stress Function (ASF) come combinazione lineare delle soluzioni di Michell e dei termini incogniti: Il comando “sum” permette di eseguire una sommatoria e vuole come primo parametro il termine generico della sommatoria (funzione di una variabile di scorrimento), quindi la variabile di scorrimento e poi i suoi estremi di variazione.

Dopo aver determinato l'espressione della ASF, si possono ricavare, mediante le relazioni apposite (pag.110 Barber), le componenti di tensione in funzione dei coefficienti incogniti:

Imponendo le condizioni al contorno discusse nella parte teorica, si ottengono cinque equazioni in nove incognite che inseriamo nella lista “eqns”. Risolvendo tale sistema si ricaveranno i coefficienti incogniti della combinazione lineare.

Avendo più incognite che equazioni, si impone che quest’ultime siano soddisfatte per ogni valore assunto da sin(2θ) e cos(2θ), poiché le equazioni sono lineari rispetto a queste due quantità. Per far ciò si calcola il residuo, definito come la differenza tra la parte sinistra (lhs) e destra (rhs) di ogni equazione. I termini in sin² e cos² che compaiono nella parte destra di alcune equazioni si esprimono in funzione di sin(2θ) e cos(2θ) applicando il comando “trigreduce”.

I residui così calcolati devono annullarsi per ogni valore assegnato a sin(2θ) e cos(2θ) e essere costanti rispetto a queste quantità, cioè le loro derivate devono essere uguali a 0. In questo modo si definisce la lista di equazioni “definitive”.

Maxima valuta automaticamente uguale a 0 equazioni che non sono diversamente specificate.

Il comando “append” permette di unire una serie di liste in un’unica lista.

Risolvendo il sistema di equazioni nelle incognite “unks”, tramite il comando “linsolve”, si ricavano i singoli coefficienti. Si noti come Maxima elimina automaticamente equazioni linearmente dipendenti da altre.

Inserendo il comando “globalsolve=true”, i valori appena calcolati vengono assegnati automaticamente ai coefficienti incogniti e quindi sostituiti anche nelle espressioni dei componenti dello sforzo.

In questo caso si è riusciti a risolvere il sistema perché il numero di equazioni dipendenti presenti in esso (6) è pari alla differenza tra il numero delle equazioni (15) e quello delle incognite (9). Se le equazioni dipendenti fossero state una di meno o una di più, il sistema sarebbe stato rispettivamente impossibile o con soluzione parametrica.

A questo punto è possibile plottare l’andamento delle tensioni che agiscono al bordo del foro (r=1). Il comando usato in Maxima per la realizzazione del grafico è “plot2d”, a cui bisogna passare come primo elemento la lista delle funzioni da rappresentare e come secondo la lista contenente la variabile indipendente e i suoi estremi di variazione. Se si vuole si può inserire una legenda, definita come una lista che ha per primo elemento la parola chiave “legend”, seguita dai nomi che si vuole far apparire, racchiusi tra doppi apici. Si può anche aggiungere l’intervallo di variazione dell’asse delle ordinate, inserendo una lista che comprende la parola chiave “y”, seguita dai suoi estremi di variazione.

Le relazioni d'interesse sono:

• tensione circonferenziale vicino al foro
• tensione radiale di far field
• tensione circonferenziale di far field
• tensione tangenziale di far field

Il grafico che si ottiene è quello riportato di seguito:

Se si vuole che il grafico appaia in linea con il codice e non in una finestra a parte, si usa, al posto di “plot2d”, il comando “wxplot2d” (a cui vanno passati gli stessi argomenti).

Come si può notare dal grafico si è ottenuto uno stato tensionale simmetrico (coerente, data la simmetria della struttura e del caricamento). In particolare, si osserva che il quadratino elementare, localizzato sul bordo del foro a θ=0° e a 180°, è circoferenzialmente compresso da 1 MPa mentre quello a θ=90° e θ=270° è sottoposto ad un’azione trattiva pari a 3 MPa. Questo risultato è in linea con quanto ci si aspettava: il valore del fattore di forma, ovvero il rapporto fra tensione teorica e nominale, in prossimità del bordo libero per un foro infinitesimo in una lastra a trazione (si ricorda che stiamo studiando la struttura equivalente in cui il foro è sì di dimensioni finite, ma in una lastra infinita) è infatti di 3 (vedi A. Strozzi - Costruzione di Macchine, pag. 315).

Modificando lo stato tensionale a remoto, il codice fornisce l’andamento corrispondente. Ad esempio, sottoponendo il sistema solamente a una tensione tangenziale unitaria a remoto (quindi σ_{x_ff}=0, σ_{y_ff}=0 e τ_{xy_ff}=1), si trova che i quadratini elementari localizzati a θ=45° e θ=225° sono sottoposti a una compressione circonferenziale di 4 MPa mentre quelli a θ=135° e θ=315° subiscono una tensione trattiva di 4 MPa. I punti invece caricati nel caso precedente risultano essere scarichi.

Altri casi visti a lezione sono:

• σ_{x_ff}=1, σ_{y_ff}=1 e τ_{xy_ff}= 0 (stato idrostatico piano)
• σ_{x_ff}=1, σ_{y_ff}=-1 e τ_{xy_ff}= 0 (stato uguale a quello sottoposto a sola tensione tangenziale, ma sfasato di 45°)
• σ_{x_ff}=0, σ_{y_ff}=0, τ_{xy_ff}= 0 e σ_rr=-1 (caricamento a remoto nullo e pressione sul bordo interno; il valore della tensione radiale è da sostituire nelle condizioni al contorno)

Per determinare il sistema di equazioni definitivo, si può procedere diversamente rispetto a quanto fatto precedentemente, imponendo che il residuo sia nullo per un certo numero di valori specifici arbitrari di θ. Si ottiene così così un sistema di equazioni che permette di calcolare i coefficienti incogniti. Si controlla quindi che i valori appena calcolati annullino i residui per qualsiasi valore assunto da θ (se il residuo si annulla l’equazione è verificata).

Il numero di valori specifici da sostituire a θ deve essere tale da ottenere una quantità di equazioni indipendenti sufficiente per determinare le incognite del sistema. Ad esempio, si valutano le equazioni per tre valori di θ (0°, 45° e 60°) e si risolve il sistema corrispondente, determinando le soluzioni di tentativo.

Un altro modo ancora con cui si può procedere per determinare il sistema definitivo di equazioni consiste nell’integrare il residuo in θ con funzioni peso diverse, in maniera tale da eliminare la dipendenza delle equazioni dall’angolo. Anche in questo caso il numero di integrazioni deve essere tale da ottenere un numero sufficiente di equazioni indipendenti.

Si risolve quindi il sistema così ottenuto, verificando poi che le soluzioni calcolate annullino i residui per ogni possibile valore di θ.

Nella definizione delle funzioni in questa trattazione si è usato il comando “define” e non “:=” in quanto la valutazione della funzione doveva essere fatta immediatamente all'atto della definizione e non all'atto dell'introduzione degli argomenti specifici.

Esistono prevalentemente due modi per definire le funzioni in Maxima, ovvero con “:=” oppure con il comando “define”. Il primo metodo è quello un po' meno affidabile, si faccia riferimento ad un esempio semplice, dove è stata definita la funzione “potenza”.

Definire una funzione con “:=” indica che la potenza è funzione di due argomenti, dove il primo verrà inserito nel segnaposto “base”, mentre il secondo sarà associato al segnaposto “esponente”.

Il problema che può nascere con questa definizione è dato dal fatto che la valutazione della funzione viene ritardata all'atto del passaggio dei due argomenti specifici; infatti se ora definissimo il valore del segnaposto “esponente”, la funzione non viene valutata con il valore passato in quanto il segnaposto ha cambiato nome in “b”.

La funzione “define” invece valuta la funzione immediatamente all'atto della definizione.

Andando a passare dei valori agli argomenti:

La differenza risulta lampante quando vario la funzione introducendo un termine “pippo” all'esponente. Nel caso “:=”:

Nel caso “define”:

Quando, nel valutare un’equazione, Maxima restituisce, per le variabili d’interesse, dei valori intermedi anziché gli ultimi calcolati si può ricorrere al comando “infeval”, che ripete la valutazione fino a quando il risultato di due successive non è uguale.

Si consideri il seguente esempio:

Si eseguono delle valutazioni, prima iterando il comando “ev” e poi abbinandogli “infeval”:

“infeval” non è da usare quando ci sono delle sostituzioni ricorsive, perché non si hanno mai due sostituzioni successive uguali e il comando continua ad eseguire cicli senza mai fermarsi.

Ad esempio, si può osservare che se definisco:

Applicando “infeval”:

Il comando cicla tra due soluzioni successive che danno sempre risultati diversi.

Considerando la trattazione della lastra forata, se, dopo aver trovato i valori dei coefficienti incogniti (senza inserire “globalsolve=true” dopo il “linsolve”), si chiede di valutare la tensione radiale usando il comando “ev” (anche più volte), si nota che Maxima non sostituisce i valori delle incognite. Ricorrendo invece al comando “infeval”, viene subito effettuata la sostituzione dei coefficienti appena calcolati.

Con lo stesso procedimento visto per la lastra forata si riesce a determinare il carico agente su una cella di carico anulare.

La cella di carico è costituita da un anello abbastanza spesso, posto tra un piano rigido e un corpo mobile su cui viene applicato un carico F da misurare. Sul bordo interno o esterno dell’anello vengono applicati degli estensimetri, la cui deformazione è ricollegabile all’entità del carico.

Le condizioni al contorno prevedono che il bordo interno sia scarico e che il bordo esterno sia scarico tangenzialmente e sottoposto a una tensione radiale compressiva -σ_r, la quale ha un andamento come una δ di Dirac centrata in π/2 e in 3/2 π.

Rappresentando le δ di Dirac in serie di Fourier e sommandole, si ottiene: σ_r=a₀+a₂*sin(2θ)+a₄*sin(4θ)+…

Come condizione al contorno al bordo esterno si ha quindi una tensione radiale definita come somma di coefficienti in serie di Fourier, che permettono di rifarsi allo stesso metodo risolutivo usato per la lastra forata.

Si vuole determinare la rigidezza della maglia di una catena mediante la teoria della trave: la trave è considerata rettilinea per il tratto dritto della maglia e curva per il tratto curvo.

L'asse della maglia può essere pensato composto da due tratti rettilinei, ciascuno di lunghezza 2L, e da due semicirconferenze di raggio r. La sezione è circolare di diametro d.

Sulla maglia agiscono due carichi concentrati di intensità F alle estremità. La struttura presenta carichi ma non vincoli, ciononostante il problema ha senso, in quanto i carichi esterni sono in equilibrio.

Il corpo presenta due piani di simmetria ortogonali al piano xy. Poiché il sistema risulta simmetrico e caricato simmetricamente, esso si deforma e si tensiona simmetricamente. Per questo motivo è lecito considerare solamente 1/4 di struttura. Per fare ciò è necessario introdurre vincoli di simmetria che garantiscano la compatibilità cinematica della struttura: si vuole infatti garantire l'assenza di compenetrazione e di distacco di materiale tra la porzione modellata e le restanti. Per ogni piano di simmetria si identificano 3 direzioni: una ortogonale e due parallele. I vincoli di simmetria hanno il compito di bloccare gli spostamenti in direzione normale al piano e le rotazioni entropiano. Considerate tali condizioni sugli spostamenti, si inseriscono due doppi pendoli.

Si noti che il carico passa da F a F/2 in quanto l’altra metà è applicata nel punto simmetrico ad A.

In questo modo la struttura risulta una volta iperstatica. Per renderla isostatica si sostituisce in A un doppio pendolo con un carrello e si introduce l’incognita iperstatica C_A, legata alla coppia del punto in cui è stato eliminato il vincolo. Per garantire la compatibilità cinematica si pone ψ_A=0.

Si sono indicati con N_A, N_C, C_A e C_C gli sforzi normali e i momenti in A e in C (secondo la teoria della trave curva sono considerate positive le coppie che tendono l’intradosso).

Il procedimento risolutivo consiste nel ricavare le reazioni N_A, N_C e C_C (determinabili per solo equilibrio) e le azioni interne lungo la maglia al fine di trovare l’energia potenziale elastica, che risulterà funzione di C_A e F. Attraverso quest’ultima si riesce a ricavare il valore di CA che consente di avere ψ_A=0 (ripristinando la compatibilità con il doppio pendolo). In questo modo l’energia potenziale dipende solo da F e derivandola rispetto a questa quantità si determina la rigidezza e l’allungamento della maglia.

Si definiscono e risolvono le equazioni di equilibrio alla traslazione orizzontale, verticale e alla rotazione attorno al punto O (si considerano positivi i contributi antiorari).

Si vanno a determinare ora, sul tratto curvo della maglia, le azioni interne, funzioni di θ (angolo compreso tra A e B).

foro_in_lastra_infinita_v000ok.wxmx

foro_in_lastra_infinita_v001.wxmx

foro_in_lastra_infinita_v002.wxmx

Formula per l'energia interna di una trave curva nel piano. Lo sforzo normale $N$ è supposto positivo se trattivo, il momento flettente $M_f$ è supposto positivo se tende le fibre all'intradosso (ossia se tende a raddrizzare la trave); nel caso questa seconda convenzione non sia rispettata occorre variare il segno del termine misto $M_f N$.

$$ \def\d{\,\mathrm{d}} U= \int_{0}^{\Phi} \left( \frac{M_{f}^2 }{2 E A \delta r_g} + \frac{N ^2}{2 E A} +\xi \frac{T ^2}{2 G A} - \frac{N M_{f}} { E A r_g} \right) r_g \d \phi $$

ove $A$ è l'area di sezione, $r_g$ è il raggio baricentrico (supposto costante), $\delta=r_g-r_n$ è la distanza tra questi è il raggio neutro, e, per sezioni circolari piene, $\xi= 1.11$, e

$$ r_n = \frac{\left(r_e-r_i\right)^2}{8\left( \frac{r_i+r_e}{2} - \sqrt{r_i r_e} \right)} $$

ove $r_i,r_e$ corrispondono ai raggi interno ed esterno.

maglia_di_catena_2018_v000.wxmx