Si vuole analizzare la distorsione presente in un elemento a quattro nodi isoparametrico, definito in Marc Mentat come Elemento 3. Nel nostro caso specifico realizziamo un elemento formato da quattro nodi nei punti 1(0,0,0) ; 2(0.3,0.6,0) ; 3(1,1,0) ; 4(0,1,0) vincolato isostaticamente mediante carrello nel punto 4 (direzione in X) e cerniera nel punto 1 (direzione in X e Y) e caricato da una forza F=1N nel punto 3 diretta con verso –Y.

Per prima cosa si inseriscono i quattro nodi nelle coordinate (0,0,0) ; (0.3,0.6,0) ; (1,1,0) ; (0,1,0) Si realizza l’elemento a quattro nodi impostando Element class quad(4) e selezionando i nodi in senso antiorario per ottenere una circuitazione positiva.

Selezionando element class quad(4), si realizza un elemento 3. In Marc Mentat, si definisce elemento 3 un elemento a 4 nodi, isoparametrico. Si tratta di un quadrilatero scritto per applicazioni in plane stress. Vengono usate funzioni di interpolazione bilineare. La rigidezza viene calcolata utilizzando 4 punti di Gauss.

Si procede ora ad effettuare verifiche sulla qualità della Mesh entrando nel menù Check. Utilizzando il comando upside-down è possibile verificare che nessun elemento risulti invertito. Utilizzando il comando distorted è possibile verificare se sono presenti distorsioni (calcolo dello Jacobiano) e nel nostro caso ci dice che è presente una distorsione. Utilizzando il comando aspect ratio è possibile determinare il rapporto perimetro/area.

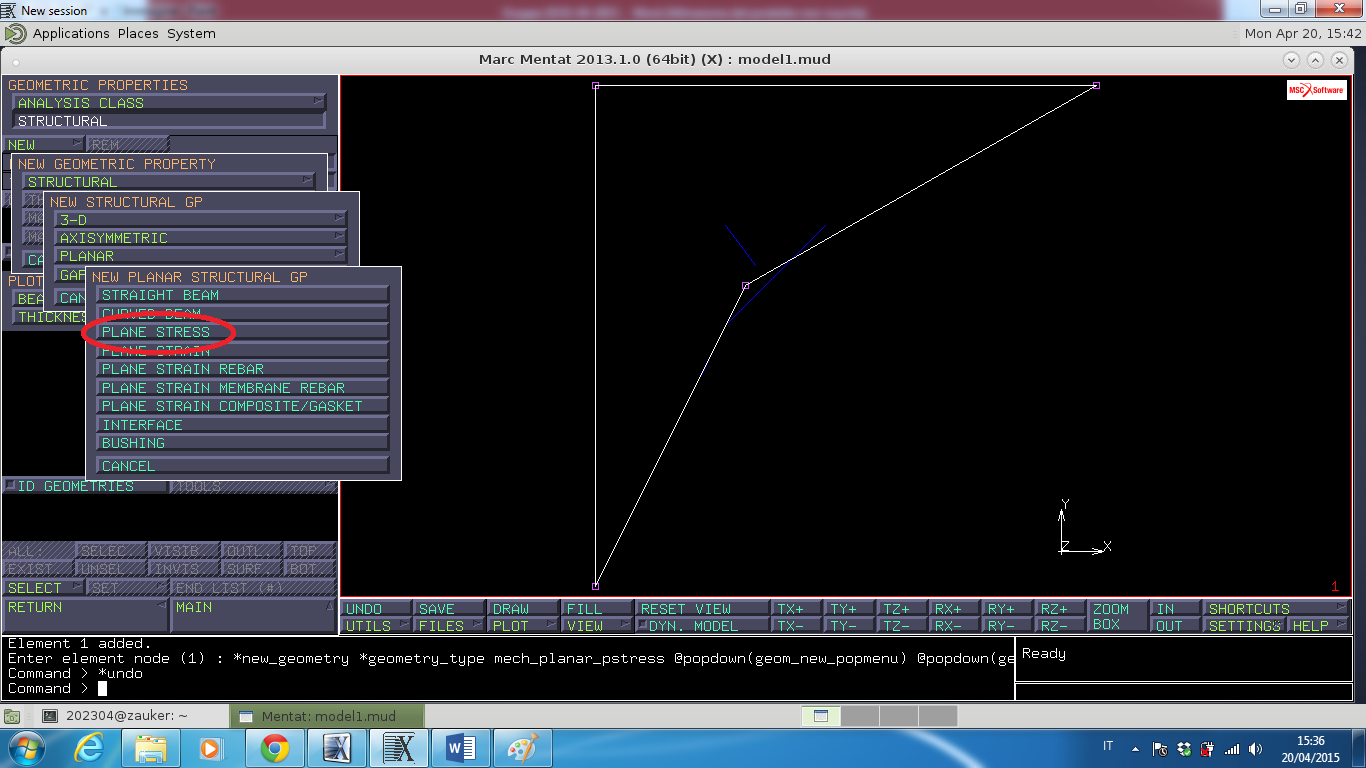
Si seleziona Plane Stress dal menù Geometric Properties e in Poperties si impone uno spessore (Thickness ) di 1 mm.

Si definisce il tipo e le caratteristiche del materiale, che nel nostro caso è alluminio avente modulo di Young E=70000, coefficiente di Poisson ν=0.33 e densità ρ=2,7

Si impongono ora le Boundary Conditions applicando di due vincoli (cerniera e carrello) e la forza F La cerniera, applicata nel punto 1, vincola in X e Y Il carrello, applicato nel punto 4 vincola in X La forza viene applicata sul punto 3 ed ha intensità di 1 N con verso –Y

Si seleziona Structural e nelle Properties si imposta Analysis Dimension Plane Stress.

In Job result si selezionano stress, elastic strain ed equivalent Von Mises Stress.

Lancio il Jobs e mi restituisce errore 13, causato dalla distorsione presente nell’elemento.

È possibile notare come il calcolo errato dello Jacobiano influenzi la corretta determinazione della Mesh con conseguente errore. Se si ha un elemento al limite della distorsione (Jacobiano nullo o infinito) la rigidezza calcolata è sbagliata. Pertanto occorre realizzare mesh corrette per evitare errori di calcolo di questo tipo.

Data una trave incastrata ad un estremo e caricata da una forza all’estremo opposto si vuole confrontare il risultato calcolato a FEM (Marc Mentat) con i calcoli analitici mediante la teoria della trave con il teorema di Castigliano. L’uso di travi nei progetti di telai riguardano la modellazione di sospensioni. Si realizza una trave di lunghezza 400mm incastrata ad un estremità e caricata da un carico P di 5N all’estremità opposta. La trave è di sezione rettangolare con altezza 6mm e larghezza 30mm. Il materiale è alluminio avente modulo di Young E=70000, coefficiente di Poisson ν=0.33 e densità ρ=2,7.

In un sistema elastico, la derivata parziale dell'energia totale elastica rispetto ad una forza (o coppia) definisce lo spostamento (o rotazione) del punto di applicazione nella direzione di applicazione della forza (o coppia). L’energia totale elastica risulta

\(U=\int\limits_0^l \frac{Mf^{2}}{2EJ} = \int\limits_0^l \frac{P^{2} x^{2}}{2EJ} dl = \frac{P l^{3}}{6EJ} \)

La freccia invece

\(\frac{\partial U}{\partial P}= \frac{P l^{3}}{3EJ} = 2,82mm\)

Il momento d’inerzia è pari a

\(J= \frac{b h^{3}}{12}=540 mm^4\)

Si procede ora alla realizzazione della mesh e all’analisi FEM.

Si costruisce un elemento line(2) formato da due nodi nei punti (0,0,0) ; (400,0,0).

Si suddivide l’elemento in 100 parti. Si esegue lo sweep per completare la mesh.

Si immettono le proprietà geometriche in planar straight beam, questo è un elemento 5. L’elemento 5 è un elemento a due nodi in sezione rettangolare con interpolazione lineare parallela alla sezione dell’elemento e cubica rispetto alla normale. Si inserisce l’altezza di 6mm e l’area 180mm2, il terzo data field non è utilizzato. L’altezza è la dimensione ortogonale all’asse disegnato.

Si inseriscono le proprietà del materiale considerando alluminio che ha modulo di Young E=70000, coefficiente di Poisson ν=0.33 e densità ρ=2,7. Il procedimento di inserimento dati è uguale al caso visto in precedenza.

Si impostano ora le Boundary Condition ricordandosi che l’elemento trave ha ai nodi 3 gradi di libertà. Il vincolo dell’incastro nel primo nodo va delineato chiamando il fixed displacement “incastro” e bloccando i primi 3 gradi di libertà. Questo è sbagliato, in quanto dovrei bloccare la rotazione intorno all’asse Z ma, per un errore interno al software, si bloccano gli spostamenti in X,Y,Z.

Il carico sul nodo 2 da inserire è di 5N in direzione -Y.

una volta terminata le operazioni è possibile lanciare il jobs impostando in analysis dimension 2D ed in jobs results selezionare stress, elastic strain, equivalent Von Mises stress, Beam axial force, Beam bimoment (??? ndEB).

Il bimoment è caratteristico delle travi a torsione con warping (parzialmente) inibito; per ottenere il momento flettente selezionare invece il Beam Bending Moment Local X.