Nel file Maxima comandi_gruppo_16.wxmx sono elencati e spiegati i seguenti comandi spiegati a lezione.

• ratsubst
• sqrt
• assume
• forget
• makelist
• wxplot2d
• trigsimp
• trigexpand
• solve
• realpart
• imagpart
• ev
• exponentialize
• demoivre
• quad_qag
• zeromatrix
• transpose
• genmatrix
• lambda
• augcoefmatrix

Il metodo degli elementi finiti (FEM) è un procedimento di discretizzazione che, attraverso l’uso di un modello matematico e di tecniche di calcolo numerico, rende possibile lo studio di problemi particolarmente complessi. Sulla base delle equazioni fondamentali che regolano il fenomeno allo studio, mediante un’opportuna approssimazione delle variabili in gioco, viene ricercata una soluzione che, pur non essendo esatta, fornisce indicazioni utili per l’analisi in problemi la cui soluzione per via analitica, coi metodi classici, risulterebbe onerosa.

Per quanto riguarda la meccanica delle strutture possono essere affrontati problemi lineari elastici, ma anche problemi di elasticità non lineare e di plasticità, problemi statici, stazionari, dinamici ed anche di meccanica impulsiva. Il metodo degli elementi finiti si adatta bene nel risolvere problemi che hanno domini complessi (come il telaio di una vettura).

L’obiettivo è di arrivare a scrivere per un certo numero di elementi significativi una relazione di rigidezza e di poter scrivere delle relazioni che permettano di esprimere il campo degli spostamenti, delle deformazioni e delle tensioni in tutto l’elemento, a partire dai valori degli spostamenti nodali. In poche parole noti gli spostamenti posso conoscere tutto. Infatti nell’impostazione del nostro problema consideriamo gli spostamenti come incognite.

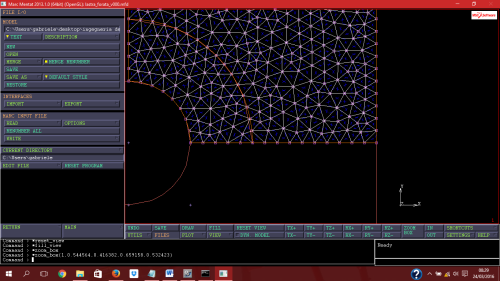
Il principio ingegneristico, sul quale il metodo ad elementi finiti si basa, è quello del divide et impera . Perciò si discretizza il continuo, che ha infiniti gradi di libertà, con un insieme di elementi di dimensioni finite (mesh), tra loro interconnessi in punti predefiniti (nodi). Un esempio di mesh (discretizzazione) del dominio di calcolo è mostrato in figura:

La mesh o griglia è una struttura reticolata costituita da un numero considerevole di elementi finiti collegati tramite nodi, è composta da geometrie di forma matematicamente definita (triangoli, quadrilateri, esaedri, tetraedri).

I vantaggi dell’analisi strutturale FEM:

• la possibilità di prevedere il comportamento del prodotto, evidenziando quelli che saranno i punti di forza e i difetti;
• possibilità di eseguire già in fase di studio le ottimizzazioni che altrimenti dovrebbero essere eseguite sul prototipo fisico;
• abbattimento dei costi dovuti al elevato numero di iterazioni make & try tra prototipo e prova.

Il programma utilizzato è Marc della MSC Software, con il software Mentat come interfaccia grafica. Con il quale viene analizzata la struttura di una lastra piana forata sottoposta a carico di trazione.

Prima di aprire Marc si deve scaricare dal wiki il file “lastra_forata_v000.mfd” presente nella relativa lezione.

scrivere la riga di comando nel prompt dei comandi → mentat2013.1 -ogl -glflush

FILES → OPEN → lastra_forata_v000.mfd → OK

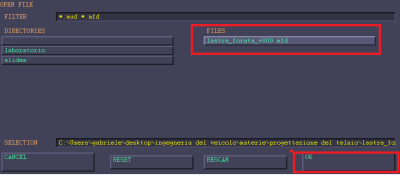
NOTA: inizialmente la lastra forata non viene visualizzata perché la nostra vista non è impostata sul piano (x,y) della lastra stessa. Per visualizzare la lastra sul piano (x,y) ovvero con asse z entrante nello schermo procedere con

RESET VIEW → FILL

Si decide di analizzare solo un quarto di lastra per risparmiare memoria RAM data la simmetria geometrica e di carico del problema.

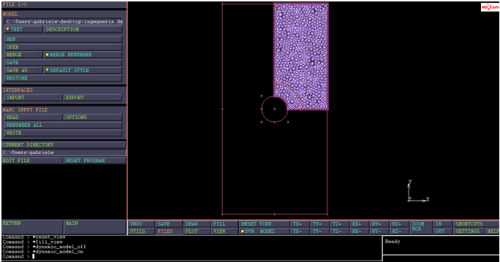
NOTA: il comando FILL modifica lo zoom per ottenere l’intero modello a schermo. Ogni qualvolta che si vuole tornare alla vista originale basta cliccare

RESET VIEW → FILL

DYNAMIC MODEL

Cliccando sul bottone DYN. MODEL e accendendo il led laterale, posso utilizzare il mouse per ingrandire l’oggetto o per ruotarlo modificando la vista a piacere.

Spegnendo il led del pulsante DYN. MODEL, il mouse selezione gli oggetti e permette di selezionare i vari menù.

MOUSE

Tasto sinistro del mouse traslo la vista attorno al modello.

Tasto destro ingrandisco o riduco la vista trascinando il mouse.

Rotella premuta, ruoto il modello.

ROTAZIONI di 10° del modello attorno gli assi:

RX+ ruota in senso orario attorno all’asse x.

RY- ruota in senso antiorario attorno all’asse y.

Analogamente gli altri comandi.

ZOOM BOX

Clicco su un’area della lastra tenendo premuto il tasto sinistro del mouse, seleziono un’area rettangolare del modello che voglio ingrandire e rilascio il tasto sinistro. Una volta rilasciato mi dà una vista ingrandita dell’area selezionata.

Si ha a disposizione un solo undo (annulla), infatti al primo undo verrà annullata l’operazione precedente; ma se premuto una seconda volta verrà annullato l’annulla precedente facendo tornare la modifica precedentemente annullata. Pertanto si consiglia di salvare varie versioni del file.

MENU PLOT

Per migliorare la visualizzazione delle curve è necessario cliccare:

PLOT → CURVES → SETTINGS → PREDIFINED SETTINGS → HIGH → REGEN

Se si usano funzioni di forma non lineari capita in alcuni problemi che lo spostamento sarà discontinuo tra ogni elemento provocando così dei tagli sulla struttura non potendosi curvare. Questo implica una maggiore rigidezza del modello che ad ogni modo viene accettata per la risoluzione del problema di calcolo.

Nei lati della lastra impongo dei vincoli per evitare il moto curvilineo. Così irrigidisco la struttura originale.

NOTA: Per salvare, FILES → SAVE AS

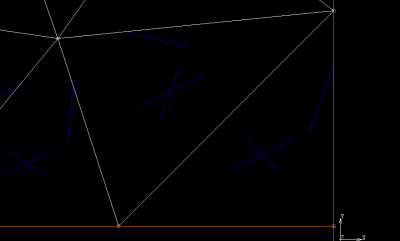
Si notano ai vertici di ogni triangolo dei quadrati che rappresentano i nodi. Ciascuno di essi ha 3 g.d.l. oppure 6 se si considerano pure le rotazioni. I lati in arancione della figura rappresentano la geometria del modello mentre i lati bianchi delimitano gli elementi finiti.

Essendo i punti del dominio infiniti e non numerabili. Bisogna ridurre le incognite a un numero finito.

Ogni nodo porta con sé da 3 a 6 incognite. Innanzitutto ne consideriamo solo 2, ossia gli spostamenti x e y. Inoltre i punti dell’elemento triangolare che non sono nodi si determinano con interpolazione agli spostamenti. Quindi sono funzioni dei nodi stessi. Vediamo come si determina lo spostamento di un punto generico P dell’elemento rispetto ai nodi.

Per ogni nodo 1,2,3 si associano due gradi di libertà, ossia gli spostamenti lungo x e y.

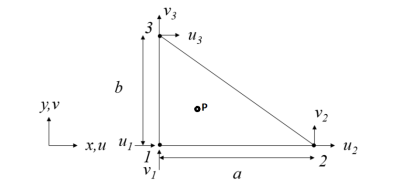
In generale un nodo presenta 6 gradi di libertà:

U_i → spostamento lungo x

V_i → spostamento lungo y

W_i → spostamento lungo z

θ_xi → rotazione attorno asse x

θ_yi → rotazione attorno asse y

θ_zi → rotazione attorno asse z

tramite interpolazione lineare si definisce lo spostamento di P in funzione degli spostamenti nodali.

Le funzioni di forma che possono definire lo spostamento del punto P sono di differenti tipologie:

• Lineare
• Quadratica
• Cubica
• Bilineare

Per semplicità di analisi scegliamo funzioni di forma lineari associate ad ogni nodo. Per il nodo i la N_i è pari a 1 nel nodo i e zero sui nodi j e k. Analogamente per le funzioni di forma N_j e N_k.

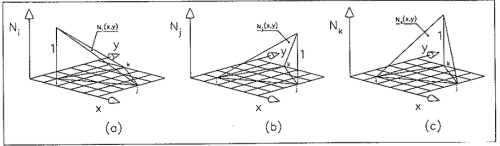
Si nota dalla figura che ogni funzione di forma genera una funzione di superficie passante per i 3 nodi .

Pertanto lo spostamento generico del punto P si definisce:

$U(x,y)= N_{i}(x,y)\times U_{i}+N_{j}(x,y)\times U_{j}+N_{k}(x,y)\times U_{k}$

• Luca Dalseno
• Alessandro Mangano
• Gabriele Spinella