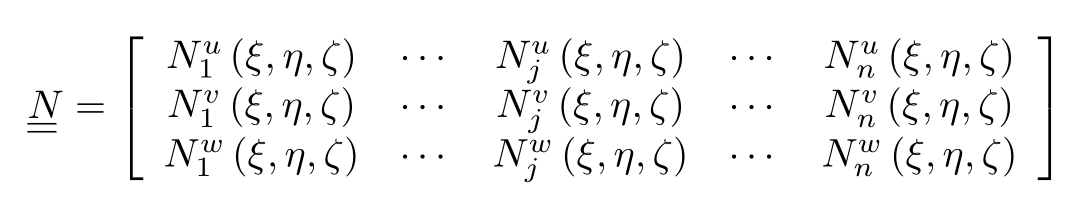Si consiglia la lettura di : breve dispensa su matrice massa

Finora sono state considerate sollecitazioni statiche, le cui proprietà non variano con le derivate temporali. È possibile definire anche sistemi quasi-statici, nei quali la sollecitazione varia nel tempo ma non influenza le quantità di interesse del sistema. I sistemi statici hanno una risposta elastica, che è completamente descritta dalla matrice di rigidezza. Di seguito andremo ad analizzare sistemi dinamici, in cui sono presenti azioni viscose e inerziali.

Partiamo dalla definizione di un elemento generico e supponiamo, per semplicità, che non siano presenti azioni viscose. Le azioni esterne sono quindi equilibrate dalle sole forze d’inerzia; avremo bisogno di definire una matrice di massa. Essa verrà definita prima per un singolo elemento, poi implementata assemblando tutti gli elementi che compongono il corpo.

Partiamo da un elemento generico, di tipo piastra a 4 nodi.

Ogni nodo ha 6gdl: $u _{i}$,$v _{i}$,$w_{i}$,$\varphi _{xi}$,$\varphi _{yi}$,$\varphi_{zi}$. Avendo 4 nodi, ho un totale di 24gdl.

Andiamo ad imporre ad ogni nodo il suo moto elementare associato allo specifico gdl. Ciò corrisponde a fissare un valore unitario di un singolo gdl per un determinato nodo e imporre nulli tutti i rimanenti gdl. In formule :

$\left\{\begin{matrix} \delta _{j}=1\\
\delta _{k,k\neq j}=0 \end{matrix}\right.$

Ognuno di questi moti elementari definisce una specifica deformata.

Per una migliore comprensione, è stato implementato un modello su Marc Mentat, scaricabile qui ¹⁾.

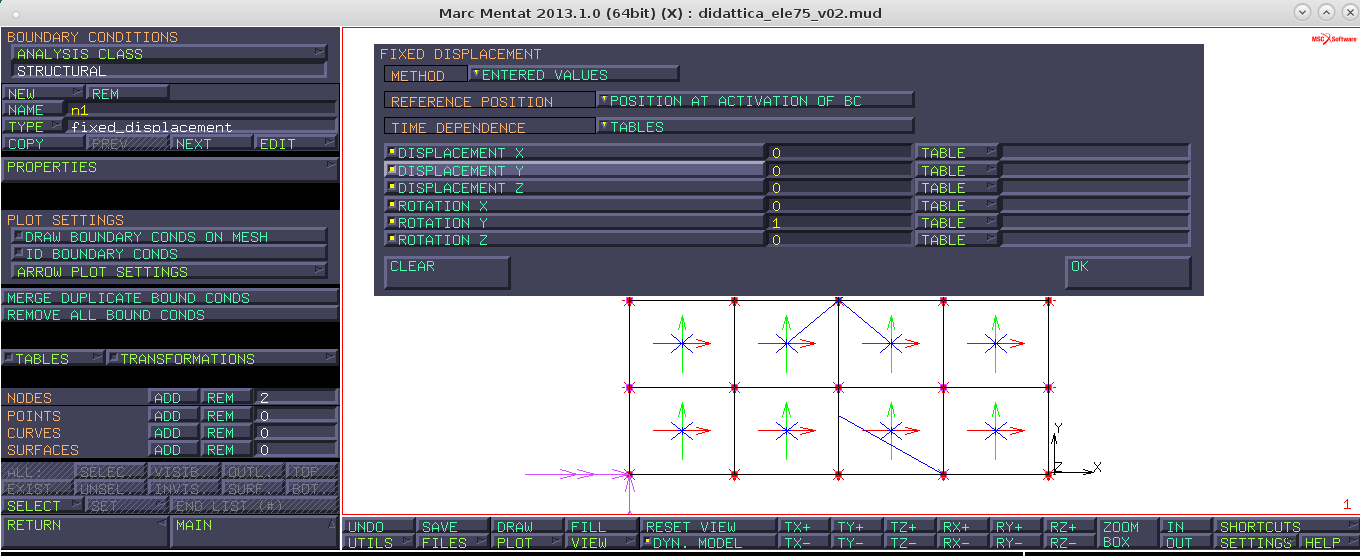
È stato utilizzato un elemento di tipo 75, cioè un elemento piastra alla Mindlin classe quad4. Si ha un’interpolazione lineare degli spostamenti in x e y, mentre viene impiegato un vincolo di corpo rigido (RBE2) per gli spostamenti in direzione z. Imponiamo sul primo nodo una rotazione unitaria attorno a y, mentre per quanto riguarda gli altri 3 nodi vengono posti nulli tutti gli spostamenti e le rotazioni. Ai comandi:

BOUNDARY CONDITION → PROPRIETIES (n1) → ROTATION Y = 1;

BOUNDARY CONDITION → PROPRIETIES (n2) → ROTATION Y = 0;

BOUNDARY CONDITION → PROPRIETIES (n3) → ROTATION Y = 0;

BOUNDARY CONDITION → PROPRIETIES (n4) → ROTATION Y = 0.

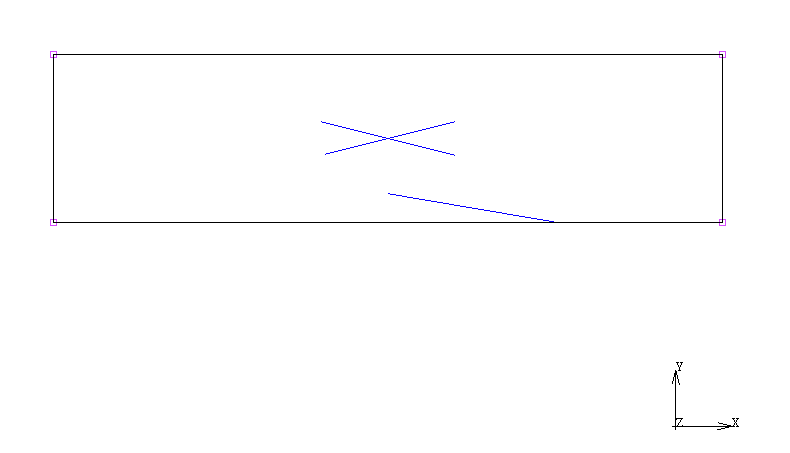
Ora lanciamo il modello, ricordando di attivare tutte le boundary condition: n1, n2, n3, n4. Otterremo così la deformata del moto elementare unitario delle rotazioni attorno all’asse y.

JOB → PROPRIETIES (.job1) → INITIAL LOADS → seleziono n1, n2, n3, n4

Nota: per una migliore visualizzazione dei risultati che otterremo andiamo a selezionare e successivamente rendere visibili gli elementi esaedri a piena integrazione (tipo 7).

JOB→ SELECT → SELECT BY → ELEMENT BY TIPE: 7

JOB → SELECT → MAKE VISIBLE

JOB → RUN → SUBMIT → OPEN POST FILES

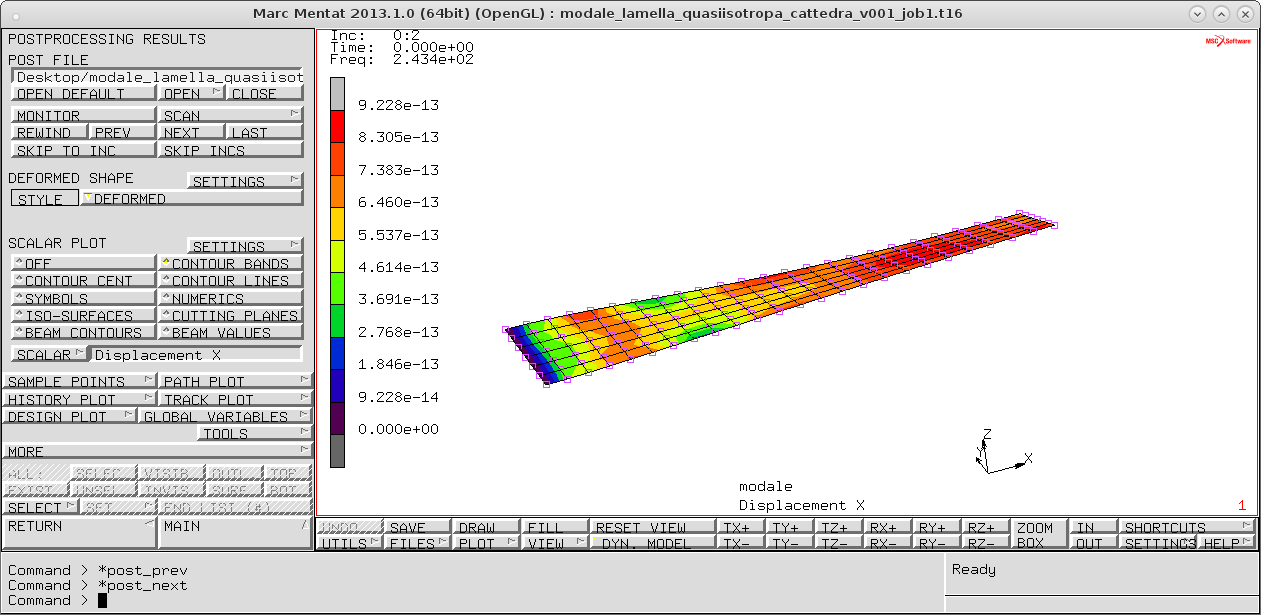
Nella figura possiamo vedere il campo di spostamenti in direzione x. Si può vedere come esso non sia costate, ma funzione delle coordinate locali $\xi$, $\eta$, $\zeta$. Possiamo adesso definire i moti elementari per tutti i rimanenti gdl, come visto sopra. È possibile scrivere gli spostamenti lungo x, y, z come :

$N_{j}^{u} (\xi ,\eta ,\zeta) \ \ \ \ N_{j}^{v} (\xi ,\eta ,\zeta) \ \ \ \ N_{j}^{w} (\xi ,\eta ,\zeta)$

Nota: dal file dei risultati ottenuti, gli spostamenti lungo la direzione z sono tutti nulli, poiché abbiamo scelto una piastra di tipo Mindlin flesso-tagliante. Se avessimo scelto invece una piastra alla Kirchhoff, cioè senza la componente tagliante, avremmo ottenuto un campo di spostamenti non nullo in direzione z. Per la piastra tipo Kirchhoff le rotazioni arricchiscono il campo di spostamenti con le derivate locali.

È possibile creare un vettore di spostamento puntuale:

$\underline{N}_{j} (\xi ,\eta ,\zeta ) = \begin{pmatrix} N_{j}^{u},
N_{j}^{v},
N_{j}^{w} \end{pmatrix}$

Affiancando tutti i vettori colonna di questo tipo, otteniamo la matrice dei moti elementari:

Viene creato il campo degli spostamenti $\underline{\delta ^{*}}$ come segue:

dove $\underline{\delta}$ è il vettore dei gradi di libertà nodali.

La matrice dei moti elementari non è funzione del tempo; derivando il campo degli spostamenti $\underline{\delta ^{*}}$ otteniamo il seguente campo di velocità:

L’energia cinetica totale è l’integrale dell’energia cinetica dell’elemento di volume infinitesimo $d\Omega (\xi ,\eta ,\zeta )$:

È possibile, attraverso passaggi, arrivare alla seguente:

dove l’espressione tra parentesi è definita come MATRICE DI MASSA $\underline{\underline{M}}$. Questa definizione è stata ottenuta da un percorso di tipo energetico, ma è anche possibile arrivare alla definizione di tale matrice tramite quadratura gaussiana. Eguagliando la variazione nel tempo di energia cinetica alla potenza fornita da un sistema di forze esterne agenti sui nodi dell’elemento otteniamo la relazione:

$\underline{\underline{M}}$ è simmetrica e definita positiva; ciò comporta che qualunque vettore di velocità non nullo deve dare un contributo di energia cinetica esclusivamente positiva.

La matrice delle rigidezze $\underline{\underline{K}}$ è invece semidefinita positiva: esistono spostamenti non nulli che generano energia potenziale elastica nulla. Questi sono i moti di corpo rigido.

Si consiglia la lettura di: dinamica delle strutture discretizzate, versione aggiornata

Ho un sistema discretizzato ed equilibrato da una forzante esterna. Tale sistema può essere scritto nella forma:

$\underline{\underline{M}}\ddot{x}+\underline{\underline{C}}\dot{x}+\underline{\underline{K}}x=F(t)$

Faccio le seguenti assunzioni:

1. Sistema di sollecitazione esclusivamente periodico;
2. Comportamento lineare.

Possiamo allora applicare il principio di sovrapposizione degli effetti: si scompone la sollecitazione periodica in una somma di armoniche e se ne considera una alla volta. Calcolo la risposta del sistema a tale armonica e infine sommo tutte le singole risposte. E' possibile scrivere una delle generiche armoniche nella forma:

$F(t)=\underline{x}\cdot e^{jwt}$

Si noti che questa forma è complessa. Si sceglie di procedere in questo modo per maggior semplicità di conti, ma il significato fisico del problema risiede solo nella parte reale della forma, che rappresenta la forza applicata ai nodi nel tempo. A regime la risposta del sistema sarà del tipo:

$x(t)=\underline{x}\cdot e^{jwt}$

La parte reale di tale quantità rappresenta lo spostamento nodale nel tempo, cioè il valore istantaneo del gdl. Sostituendo nell'equazione generale del problema otteniamo:

$(-\omega ^{2}\underline{\underline{M}}+j\omega \underline{\underline{C}}+\underline{\underline{K}})\underline{x}=\underline{f}$

Tale equazione rappresenta un sistema di n equazioni in n incognite. Possiamo quindi determinare x(t), cioè le posizioni di tutti i nodi in qualsiasi istante t, e grazie a queste ricostruiamo la deformata del sistema.

Si noti come al tendere di $\omega$ a zero l'equazione subito sopra si riconduca a quella del caso statico.

Fatto ciò si può passare all'analisi modale. Andiamo alla ricerca dei moti propri della struttura (cioè quei particolari moti periodici ammessi dall'equazione del sistema anche in assenza di forzante) permanenti nel tempo. Condizione necessaria affinché un moto perduri nel tempo è che, in assenza di lavoro fornito al sistema (cioè di forzante), non ci sia dissipazione. Dobbiamo porre la matrice C nulla.

Excursus: ciò appena detto non è sempre vero; possono esserci sistemi dissipativi che però non lavorano negli specifici moti propri. Prendiamo in considerazione l'esempio di un diapason tenuto tra due dita, che possiamo schematizzare come un sistema visco-elastico (molla-smorzatore). I modi propri del diapason considerato come oggetto continuo sono infiniti, ma quello di interesse è solo uno: quello che eccita il diapason a 440 Hz (LA4). Questo particolare modo fa vibrare i due bracci del diapason, mentre il supporto stretto tra le dita resta fermo. In questo modo non vado a far lavorare il sistema dissipativo rappresentato dalle dita e quindi non ho decadimento nel tempo.

Prendiamo allora $\underline{\underline{C}}=0$ e $\underline{\underline{K}}$ reale. Otteniamo il sistema:

$(-\omega ^{2}\underline{\underline{M}}+\underline{\underline{K}})\underline{x}=0$

Questo sistema ha soluzioni non nulle se il rango della matrice non è pieno. Le soluzioni non nulle saranno le coppie di autovalori-autovettori del tipo $(\omega ^{2},\underline{x})$ soluzioni del generico problema agli autovalori:

$A\underline{x}=\lambda \underline{x}$

Considerando che la matrice $\underline{\underline{M}}$ è definita positiva (e quindi invertibile), possiamo scrivere:

$(-\omega ^{2}\underline{\underline{M}}+\underline{\underline{K}})\underline{x}=0$

$(\underline{\underline{M}}^{-1}\underline{\underline{K}}-\omega ^{2}\underline{\underline{I}})\underline{x}=0$, dove $\underline{\underline{M}}^{-1}\underline{\underline{K}}=A$ e $\omega^{2}=\lambda$

$(\underline{\underline{A}}-\lambda \underline{\underline{I}})\underline{x}=0$

Questo è il nostro problema generalizzato, da cui possiamo ottenere $(\omega ^{2},\underline{x})$. Ognuna di queste coppie definisce un modo proprio; in particolare l'autovettore descrive la forma del modo proprio, che è da considerare a meno di una costante arbitraria, essendo gli autovalori definiti in tal senso (si ricorda che $\underline{x}$ e $\alpha\cdot\underline{x}$ sono lo stesso autovettore). Ogni modo ha quindi un'ampiezza, ma questa è completamente arbitraria e quindi di scarso interesse.

$\omega$ è invece la pulsazione del modo.

Passiamo ora a valutare i modi propri al FEM. Avendo la possibilità di scalare arbitrariamente gli autovettori, bisogna sempre controllare nel manuale del codice che si sta usando il metodo di normalizzazione degli autovettori. In Marc Mentat i modi propri vengono visualizzati in forma scalata a massa modale unitaria. Altri codici fanno diversamente (es. scalatura a norma del vettore unitaria).

Inventiamo una struttura semplice in materiale composito al fine di valutarne i modi propri: lamella rettangolare incastrata.

Lo spessore sarà dato dal processo di laminazione e verrà valutato in seguito.

Creo nuovo modello:

FILES>NEW

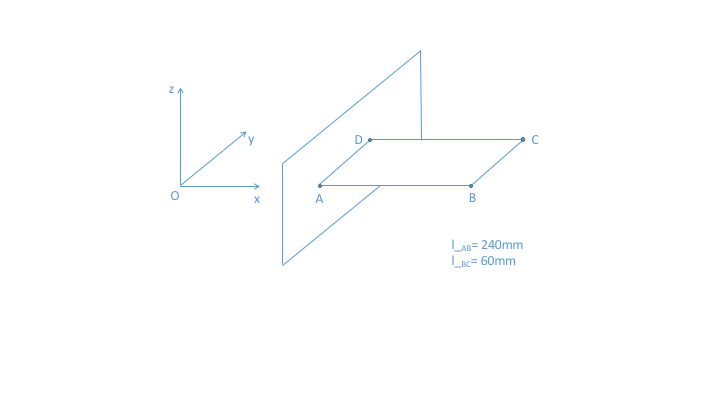
Inizio dall’inserire un unico macroelemento che andrò a raffinare in seguito. Questo elemento deve rappresentare l’intera lamella. Per l’inserimento dei nodi considero il sistema di riferimento di Figura1 centrato in A con AB giacente su x e AD giacente su y:

MESH GENERATION>NODES>ADD

0 0 0
240 0 0
240 60 0
0 60 0

Ora creo un elemento quadrilaero isoparametrico 4 nodi tra i nodi aggiunti:

MESH GENERATION>ELEMENT CLASS>QUAD(4)

MESH GENERATION>ELEMS>ADD 

Basterà selezionare i 4 nodi nella stessa sequenza nella quale sono stati riportati sopra. L’ordine si selezione risulterà importante per l’individuazione degli assi locali e quindi per l’orientazione delle fibre. Ho ottenuto tutta la mia lamella.

Scelgo la modalità di visualizzazione WIREFRAME in modo da visualizzare la freccia che indica quale è il lato 1 del quadrilatero, ovvero “asse locale 1” (sarà quello lungo AB):

PLOT>ELEMENTS>WIREFRAME>REGEN

Ora devo dividere il macroelemento in elementi elementari:

MESH GENERATION>SUBDIVIDE>DIVISIONS 

Si tratta di inserire (nei relativi box o dalla command line) il numero di divisioni volute lungo i 3 assi locali. Vogliamo elementi 10×10, quindi:

24
6
1

Applichiamo la suddivisione a tutti gli elementi:

ELEMENTS>ALL>EXIST

Per completare la mesh elimino i nodi che potrebbero essere ripetuti (vertici del macroelemento):

MESH GENERATION>SWEEP>REMOVE UNUSED>NODES

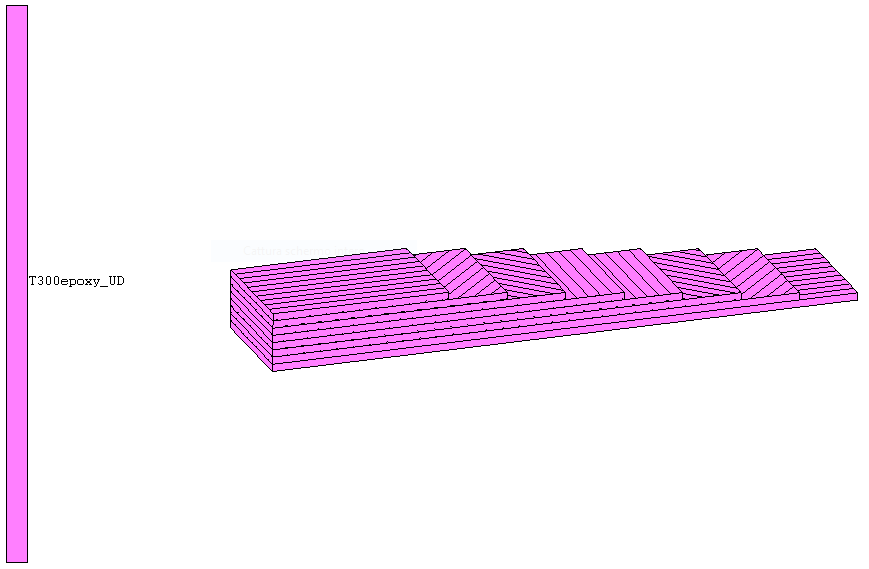
Definisco il materiale base, ovvero il materiale di una singola lamina (considerando fibra e matrice già assemblati) che possiamo trattare come materiale standard (il laminato non è standard ma composito) ortotropo. L’ortotropia del materiale indica che se identifico 3 assi e dalle normali a questi assi definisco 3 piani, allora le deformazioni taglianti saranno indipendenti su questi 3 piani. Le caratteristiche di questi materiali sono molto difficili da valutare. Usiamo dati disponibili da articoli scientifici per una fibra T300 in resina epossidica in configurazione lamina unidirezionale (solitamente i dati forniti dai fornitori non sono così completi, soprattutto nelle quantità fuori piano). Esistono anche dei database per materiali.

Szekrényes, A. "FINITE ELEMENT ANALYSIS OF A LAYERED COMPOSITE CYLINDER USING THE CONNECTION BETWEEN THE MACRO-AND MICROSTRUCTURE." (alcune unità di misura sono sbagliate, per i moduli di Young di nostro interesse l’unità di misura in questo caso è sempre GPa)

Hou, J. P., et al. "Prediction of impact damage in composite plates." Composites Science and Technology 60.2 (2000): 273-281.

MATERIAL PROPERTIES>MATERIAL PROPERTIES>NEW>STRUCTURAL

NAME>T300epoxy_UD

DATA CATEGORIES>STRUCTURAL>TYPE>ELASTIC-PLASTIC ORTHOTROPIC

Devo ora descrivere il comportamento del materiale sui 3 assi di ortotropia con le proprietà che posso trovare negli articoli riportati sopra. Quindi le direzioni di ortotropia 1,2,3 indicate dal software sono ancora generiche, associate né ai sistemi di riferimento locali degli elementi, né al sistema di riferimento fisso. In particolare la direzione 1 sarà la direzione delle fibre, perciò quella con modulo di Young massimo. Nasce un problema: il software richiede ${G_{31}}$ e ${\nu_{31}}$, mentre troviamo tabulati solo ${G_{13}}$ e ${\nu_{13}}$. Per i moduli di taglio vale ${G_{31}}={G_{13}}$, mentre per i coefficienti di Poisson no: devo trovare l’espressione della matrice di cedevolezza per materiali ortotropi (es. matrice S in https://en.wikipedia.org/wiki/Orthotropic_material) e ottenere ${\nu_{31}}$ scalando ${\nu_{13}}$ utilizzando la proprietà di simmetria della matrice, si ottiene:

$\frac{\nu_{31}}{E_{33}}=\left(\frac{\nu_{13}}{E_{11}} \right)$ ⇒ ${\nu_{31}}={\nu_{13}}\left(\frac{E_{33}}{E_{11}} \right)$ ⇒ ${\nu_{31}}=0.00141338$ (nella cella potrei anche scrivere direttamente l’espressione numerica).

Premo OK per confermare e uscire dal pannello.

Manca solo la densità (in $\frac{t}{mm^3}$) per definire completamente le proprietà del materiale:

DATA CATEGORIES>GENERAL>MASS DENSITY: 1.58e-9

Premo OK per confermare e uscire dal pannello.

Per l’analisi modale non servono informazioni sulla rottura, quindi le omettiamo. Non associamo il materiale così definito ad alcun elemento altrimenti l’elemento diverrebbe un massiccio di quel materiale. Al contrario vogliamo usare il materiale come “mattoncino”, sovrapponendo più lamine.

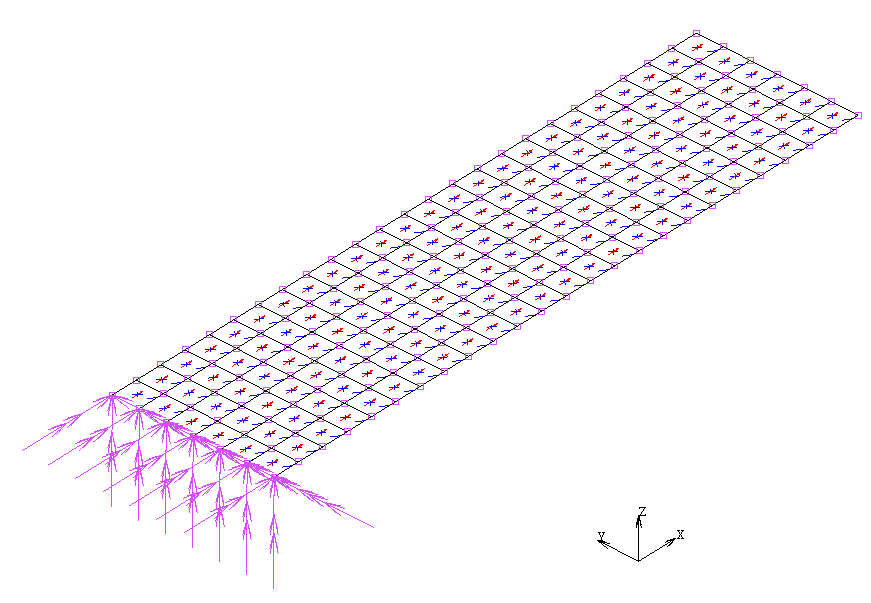
È il momento di associare assi locali degli elementi e assi di ortotropia, in particolare voglio definire quale sia la direzione dell’asse 1 di ortotropia in ogni sistema di riferimento locale. Questa sarà la direzione “0 gradi”, ovvero quella di trazione/compressione delle fibre. Per il modo in cui ho costruito il modello so che la direzione delle fibre (direzione 1 di ortotropia) sarà parallela ad AB ovvero al lato che congiunge i nodi 1 e 2:

MATERIAL PROPERTIES>ORIENTATIONS>NEW>EDGE12

Applichiamo la configurazione a tutti gli elementi:

ELEMENTS>ADD>ALL>EXIST

Vedremo comparire su ogni elemento delle frecce che indicano la direzione 1. In alcuni casi, es. superficie con doppia curvatura, descrivere l’orientazione diventa un procedimento che richiede molto tempo in quanto potrebbe essere necessario l’inserimento elemento per elemento. Esistono anche software dedicati a questa operazione.

Avendo definito la direzione “0 gradi” posso iniziare a costruire il laminato:

MATERIAL PROPERTIES>MATERIAL PROPERTIES>NEW>COMPOSITE

NAME>laminaione_quasi_isotropa_0gradi_pref_flex

DATA CATEGORIES>GENERAL

Posso ora aggiungere lamine di materiali definiti precedentemente. In particolare compongo un laminato simmetrico di 2mm costituito da lamine di 0,25mm. Parto dalla lamina più esterna:

SETTINGS>nel secondo box scelgo ABSOLUTE THICKNESS

SINGLE LAYER>APPEND>T300epoxy_UD>: THICKNESS=0.25, ANGLE=0

Eseguo la stessa operazione altre 7 volte, cambiano solo ANGLE, costruendo uno schema del genere: 0°, +45°, -45°, 90°, 90°, -45°, +45°, 0° .

Ho definito quindi un laminato a 8 lamine quasi isotropo: il comportamento quasi isotropo è quello per gli sforzi membranali, ovvero per i carichi entro piano, a flessione il comportamento è invece fortemente non isotropo: Flessione lungo x: resistenza data dalle lamine esterne a 0 gradi; Flessione lungo y: le lamine a 0 gradi sono quelle interne. Il laminato sarà cedevolissimo.

ELEMENTS>ADD>ALL>EXIST (dovrebbero risultare 144 elementi)

Definizione delle proprietà geometriche:

GEOMETRIC PROPERTIES>NEW>3-D>SHELL

NAME>piastra

PROPERTIES>THICKNESS>2 

(metto il valore coerente con lo spessore del laminato costruito, altrimenti potrei costruire il COMPOSITE con RELATIVE THICKNESS e dare il valore voluto in questa fase)

ELEMENTS>ADD>ALL>EXIST

Voglio fare l’analisi modale, quindi ho bisogno di definire le matrici Massa e Rigidezza. Per la prima ho già inserito tutti i dati che servono al software per calcolarla. La seconda invece è influenzata anche dalle condizioni al bordo, che devo ancora inserire. Se un corpo non fosse vincolato tra le modali avremmo anche moti di corpo rigido, che si presentano con frequenza nulla (o, numericamente parlando, quasi nulla) e, quindi, con periodo infinito. Saranno quindi dei moti “senza ritorno”.

BOUNDARY CONDITIONS>NEW>STRUCTURAL>FIXED DISPLACEMENT

NAME>incastro

PROPERTIES> 

seleziono tutti e 6 i gradi di libertà e mi assicuro che gli sia assegnato valore nullo. Applico tale vincolo ai 7 nodi appartenenti al piano yz.

Nel caso in cui un corpo sia caricato, ad esempio anche dal suo stesso peso, bisognerà tenerne conto attraverso un caricamento apposito? Se voglio fare un' analisi nell' intorno della condizione caricata potrò farlo, ma il carico è interessante solo per il contributo che da variando la matrice di rigidezza. Cioè è necessario mettere il carico solo se varia la matrice di rigidezza del componente ma, se la matrice di rigidezza è funzione dei carici, il problema non è lineare. Per fare quindi un' analisi di modi e frequenze proprie di un sistema non lineare (ad esempio una corda di chitarra precaricata) essendo, questo tipo d' analisi, lineare per ipotesi; si andrà a studiare il problema linearizzato nell' intorno della configurazione precaricata. Si andranno, cioè, a considerare piccoli spostamenti nell' intorno di questa configurazione, per i quali si potrà linearizzare il comportamento della struttura. Quindi i moti propri della struttura precaricata saranno da considerarsi per piccoli spostamenti dalla configurazione di riferimento (precaricata) e la linearizzazione risulterà tanto più esatta quanto più sono vicino a tale configurazione. I casi di componenti non lineari sono pochi, ad esempio: cavo pretensionato, membrane e strutture lavoranti vicine alla loro condizione di instabilità euleriana (buckling)https://it.wikipedia.org/wiki/Instabilit%C3%A0_a_carico_di_punta .

Inciso: Determinazione del carico critico per l'instabilità euleriana di un corpo snello con metodo non distruttivo: per determinare il carico limite per cui un corpo snello arriva alle condizioni di instabilità euleriana, senza rompere il componente stesso, si analizzano le frequenze proprie del corpo all' aumentare del carico. Come tirando la corda di chitarra si aumenta la sua frequenza propria, cosi una trave caricata a compressione diminuisce la propria frequenza e, al limite dell' instabilità euleriana, avrà frequenza nulla. Perciò caricando a compressione la trave e misurandone la frequenza propria all'aumentare del carico, potrò determinare la condizione di carico critico per l'instabilità (nota: non si potrà il componente alla condizione limite, altrimenti sarebbe una prova distruttiva, quando la frequenza scende sotto un certo limite si interrompe il caricamento e per interpolazione dei dati si ricava il carico critico a frequenza nulla).

Nel nostro caso lasceremo la lasta non precaricata.

Loadcase specifico per l'estrazione dei moti propri

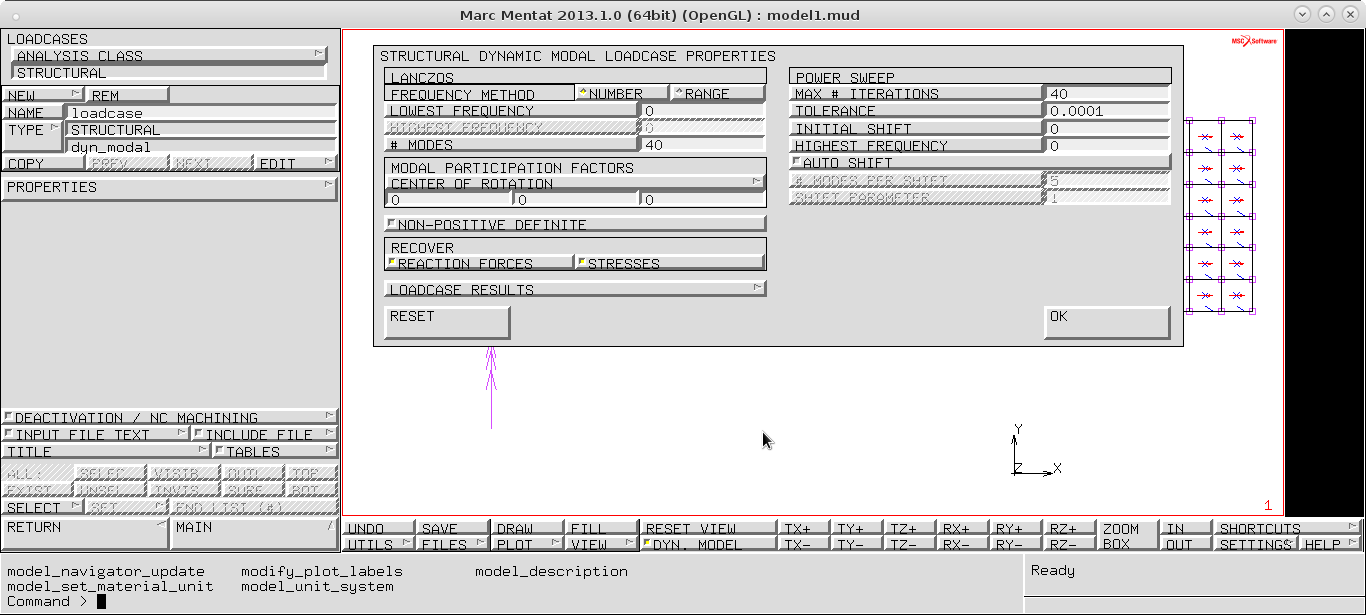
LOADCASES > NEW > DYNAMIC MODAL (è quello che ci permette di estrarre i moti propri)

name: loadcase modale

> PROPERTIES

(in dynamic modal saranno delle proprietà numeriche, cioè guidano l'algoritmo che estrarrà dalla matrice di rigidezza e dalla matrice di massa gli autovalori e autovettori del problema dinamico); ci saranno due parti del properties menu che corrispondono a due algoritmi: Lanczos e power sweep, nessuno dei quali migliore dell'altro in assoluto, si può provare con uno, se non converge, si prova con l' altro sperando che converga.

Noi useremo il Lanczos. Bisogna inserire due imput fondamentali, cioè:

- frequenza minima, ovvero, la frequenza dalla quale voglio che cominci a cercare le frequenze proprie.

<impostiamo: 0>

- # modi, ovvero, il numero di modi che voglio conoscere a partire dalla frequenza minima impostata.

<impostiamo: 40> (cioè cerchiamo i primi 40 modi propri con frequenza maggiore di 0)

A cosa serve attivare -non positive definite-? Se non abbiamo vincolato la struttura la matrice di rigidezza non sarà definita positiva. Per evitare che il programma si blocchi quando si rende conto di questo attivo la spunta; in questo modo dico al programma di essere cosciente che la matrice non è definita positiva ma voglio procedere ugualmente al calcolo. Non è detto che poi il risultato sia corretto.

NEW> STRUCTURAL

>PROPERTIES

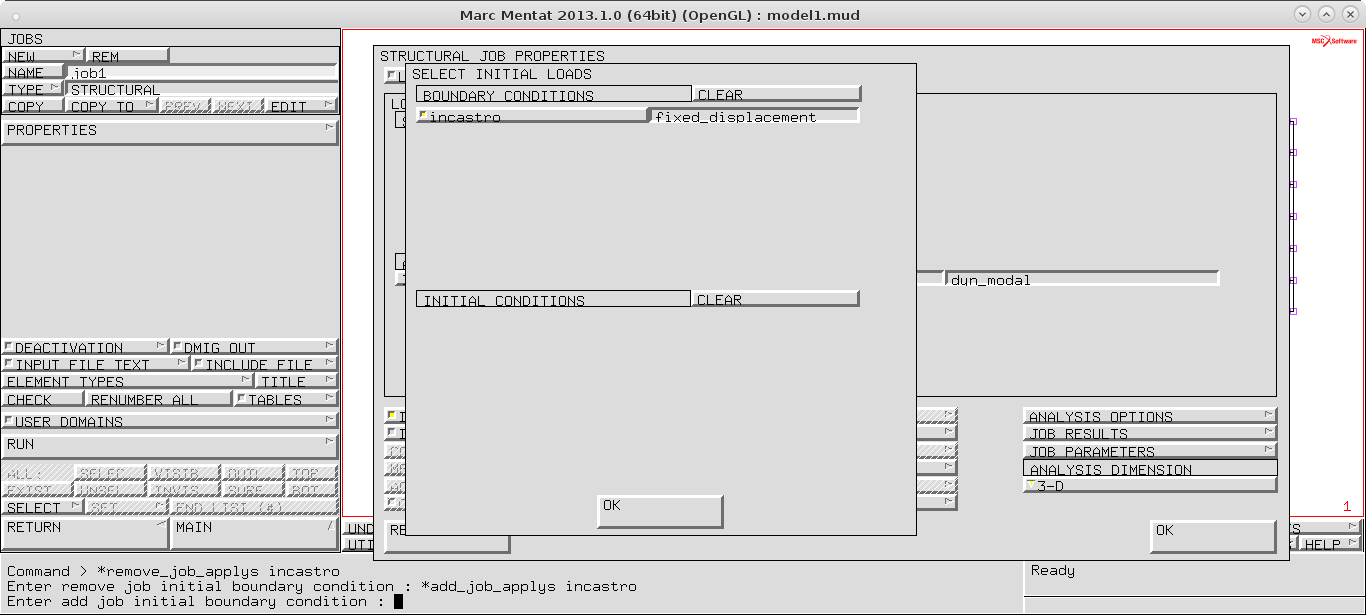
Qui si andranno a definire vincoli e carichi prima dell' estrazione dei moti propri.

>INITIAL LOADS : attiviamo il vincolo di incastro

Ora:

>STRUCTURAL JOB PROPERTIES: attiviamo il loadcase dynamic modal

In: >JOB RESULTS (in job> properties): attiviamo <stress in preferred sys> cioè: lo stress lungo gli assi di ortotropia, quindi la component11 dello stress sarà quello lungo la fibra mentre le component11 e 22 saranno in direzione trasversale alla fibra.

Come layers imponamo

<all>: in quanto non so' quale sarà la fibra a cedere

e attiviamo anche

<elastic stress in preferred sys> sempre su tutti i layers (<all>)

ora possiamo fare

>RUN >SUBMIT> OPEN POST FILE

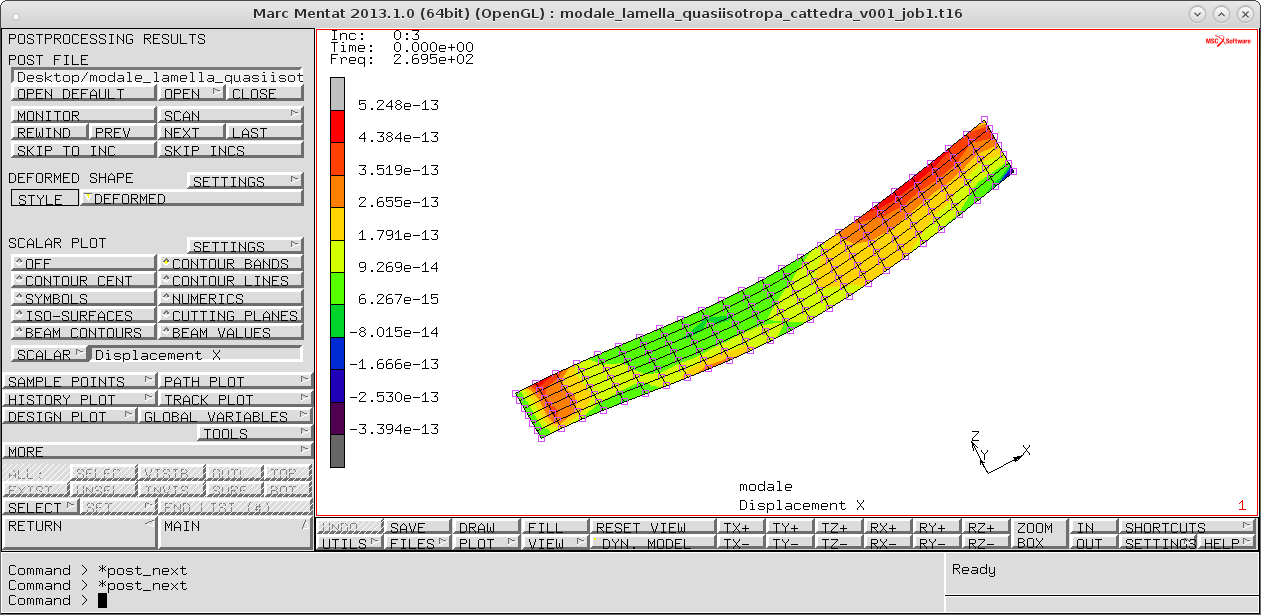
troviamo quindi le varie modali (per scorrere nei vari moti propri cliccare su next in <post file>).

In alto a sinistra nella vista della deformata si legge: numero e frequenza a cui si trova lo specifico modo proprio visualizzato.

Se in:

>deformed shape >settings >deformed scaling 

ho 1 come scalatura (scalatura di visualizzazione della soluzione), allora la deformata visualizzata sarà quella reale (con autovettori normalizzati a massa modale unitaria), cioè la posizione del generico nodo sarà individuata dalla posizione originaria del nodo più l'autovettore spostamento (normalizzato) in x, y e z di quel nodo.

Modello di fine lezione: modale_lamella_quasiisotropa_cattedra_v001.mud

Schema funzionale didattico elemento 75 (elemento piastra alla Mindlin classe quad4) per visualizzazione modi di moto elementari

link a breve dispensa su matrice massa

Proprietà materiale CFRP di esempio (T300/epoxy, lamina UD) estratte da articoli

Szekrényes, A. "FINITE ELEMENT ANALYSIS OF A LAYERED COMPOSITE CYLINDER USING THE CONNECTION BETWEEN THE MACRO-AND MICROSTRUCTURE."

Hou, J. P., et al. "Prediction of impact damage in composite plates." Composites Science and Technology 60.2 (2000): 273-281.

[curatissimissimi, vedasi coeff. di “Poison”]

dinamica delle strutture discretizzate, versione aggiornata

modale_lamella_quasiisotropa_cattedra_v001.mud

Caso di esempio: due profilati in alluminio a sezione quadra, lato 80mm alla superficie media, lunghezza 660mm, giuntati per saldatura e sollecitati da rotazione imposta. Spessori da 16 a 0.5 mm.

casi a spessore variabile a confronto (attenzione, il calcolo richiede 2Gb di ram liberi)

singolo caso (computazionalmente più leggero)

giunto_l_rigidezza_spessore.ods