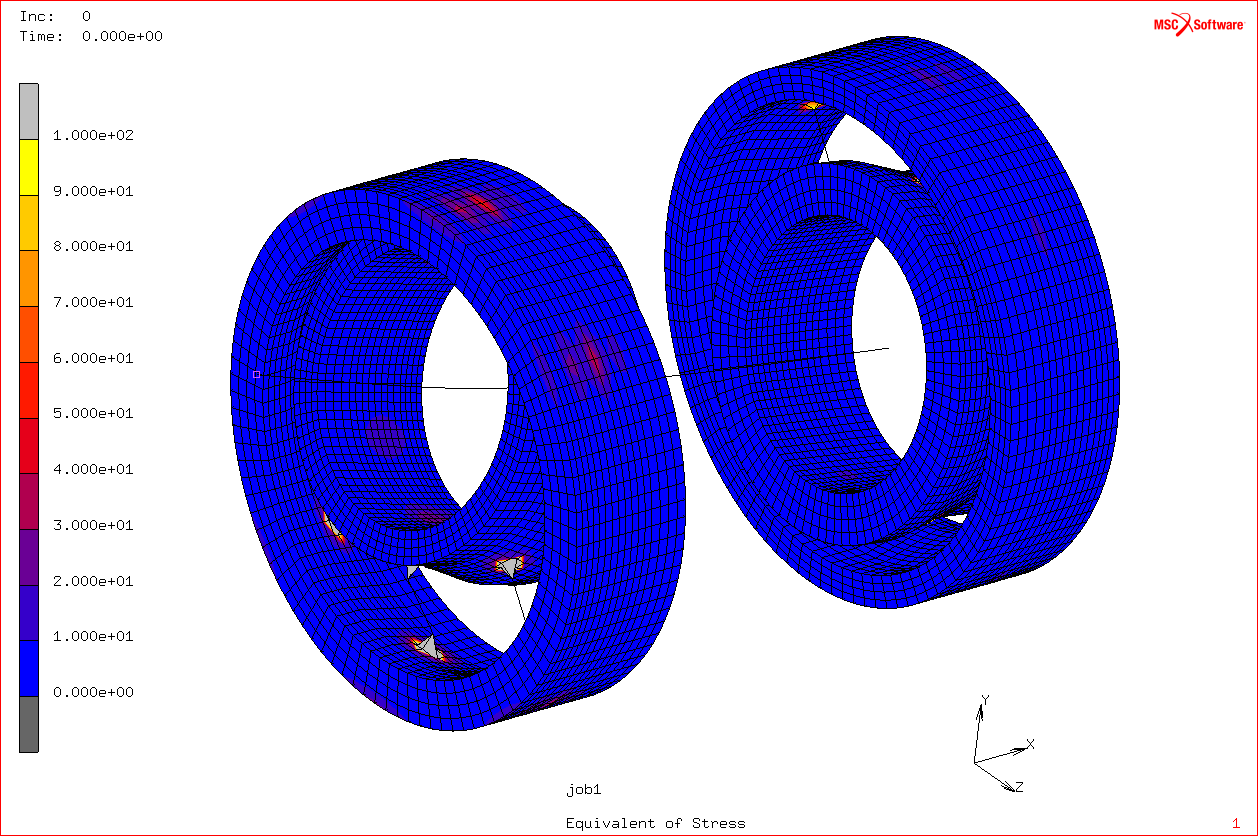Risposta ad una sollecitazione armonica
Modello di fine lezione precedente: lamella_composito_dinamica_gruppob_v001.mud
Nel modello della settimana scorsa è stato realizzato un job che, quando lanciato, estraeva i primi 40 modi propri della lamella in composito incastrata ad un estremo. La scalatura dei modi propri è stata fatta in maniera tale per cui la massa risulta unitaria: pertanto, è verificata la relazione
$\bar{δ}^T\bar{\bar{M}}\bar{δ}=1$
dove $\bar{δ}$ è il vettore spostamento (rotazione), espresso in mm (rad) ed $\bar{\bar{M}}$ è la matrice massa, espressa in tonnellate. La dimensione dell’unità sarà, quindi, tonn/mm2. È possibile visualizzare i risultati ottenuti durante la lezione precedente scaricando il modello “lamella_composito_dinamica_gruppob_v001.mud”, eseguendo i comandi JOBS>RUN>SUBMIT, cliccando successivamente su OPEN FILE RESULTS e procedendo con il tasto NEXT per visualizzare i modi propri.
| Modi Propri | Statico | Primo | Secondo | Terzo | Quarto |
|---|---|---|---|---|---|
| Freq. Naturale | 0 | 42.91 Hz | 243.4 Hz | 269.5 Hz | 747.5 Hz |
| Spost. Nodo 162 | 263.071 mm | 21.67 mm | 178.98 mm | 82.1015 mm |
Nell’analisi modale è generalmente possibile usare vincoli di simmetria ed antisimmetria modellando solo un quarto della struttura, in quanto, geometricamente, la struttura ha due piani di simmetria: il piano z-x e quello passante per il piano medio della lastra.
Quando un corpo ha piani di simmetria (o antisimmetria), i suoi modi sono simmetrici (o antisimmetrici): non esistono modi di tipo misto. In questo caso le fibre a +45° e -45° sono sfalsate in z: pertanto la struttura non si comporterà simmetricamente per via della laminazione. È possibile, comunque, usare vincoli di simmetria ed antisimmetria per sistemi simmetrici, a patto di fare tutte le combinazioni necessarie per ottenere tutti i modi propri del sistema. I modi propri trovati nella lezione precedente ci interessano perché in corrispondenza di questi, ovvero alla frequenza propria, quando una determinata forzante opera in sincrono con questa, si possono avere problemi di risonanza.
In questa lezione ci si propone di trovare la risposta del sistema ad una sollecitazione armonica: i modi propri trovati in precedenza ci permetteranno di individuare i punti di interesse. Dal punto di vista analitico, il problema si riduce alla risoluzione del sistema
$(-ω^2M+jωC+k)\bar{x}=\bar{f} \qquad [1]$
per una specifica forzante e pulsazione ω.
Il caso più semplice di forzante è il carico concentrato in un punto della lamella incastrata. Il concetto di forza concentrata, molto usato in meccanica applicata, non è equivalentemente valido per corpi elastici; applicare una forza su un’area nulla vuol dire generare pressioni di contatto infinite: un corpo elastico, sotto pressioni di questo tipo, subisce uno spostamento del punto di applicazione con singolarità logaritmica verso infinito. Pertanto, si può definire la cedevolezza di un corpo elastico come infinita e la rigidezza come nulla.
Il codice FEM non è in grado di rispondere con valori infiniti; la maniera per verificare una data risposta con gli elementi finiti è monitorare l’andamento della quantità all’infittirsi della mesh: se converge ad un valore finito, allora la quantità è finita, se cresce indefinitamente, allora la quantità è infinita. Il FEM è in grado di dare solo una risposta finita perché la forza è sempre implicitamente definita su un’area nodale. È possibile vedere la forza F concentrata come la riduzione di una pressione distribuita, di cui non è importante la natura specifica dell’applicazione.
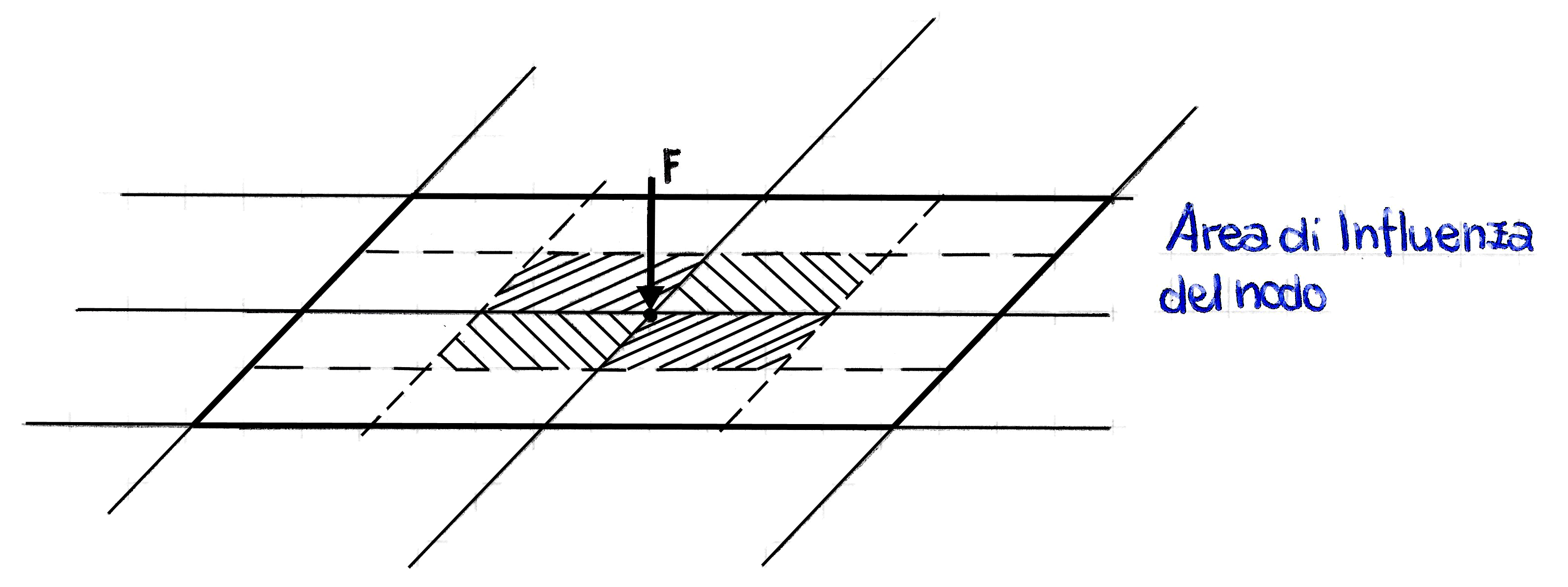
Si suppone di avere una mesh di elementi quadrilateri e di applicare una forza nodale.
Esiste una distribuzione di pressione sui quattro elementi tale per cui la risultante delle forze nodali è una forza F applicata proprio nel punto in figura. L’area di ciascun elemento varia con il quadrato della taglia dell’elemento stesso, e può essere divisa in quattro zone di influenza nodale associata a ciascun nodo adiacente; in figura, l’area di influenza A è associata al nodo 1, l’area B al nodo 2, l’area C al nodo 3 e l’area D al nodo 4. Perciò, preso un nodo in una mesh, è possibile sempre definire l’area di influenza nodale che risulta somma delle quattro aree di influenza dei quattro elementi che toccano quel nodo.
A questo punto, la forza concentrata risulta essere definita sull’area nodale: pertanto la pressione è data da
$pressione=\frac{forza\ concentrata}{area\ nodale}$
ed aumenta all’infittirsi della mesh (perché diminuiscono le aree di influenza).
Il FEM non da mai risposte di cedimenti infiniti, perché non ha il concetto di forza concentrata.
La stessa cosa vale per forze applicate su unità di lunghezza: un elemento piastra è in grado di sopportare carichi lineici perché i carichi sono distribuiti implicitamente sullo spessore dei segmenti rigidi normali al piano medio (che non diminuiscono in base alla taglia dell’elemento).
Un problema che richiede l’applicazione di un carico concentrato nel modello ad elementi finiti, dunque, è generalmente un problema mal posto. Un tipico esempio di un problema di questo tipo lo si può trovare consultando la lezione 19 del corso di Progettazione Assistita dell’anno scorso.
Tale problema è mal posto perché la rigidezza è strettamente funzione della taglia dell’elemento, perciò all’infittirsi della mesh questa tende a 0; sarebbe stato ben posto solo se fosse stata assegnata la taglia dell’elemento, quindi implicitamente indicata l’area su cui si spalma la forza dei cuscinetti.
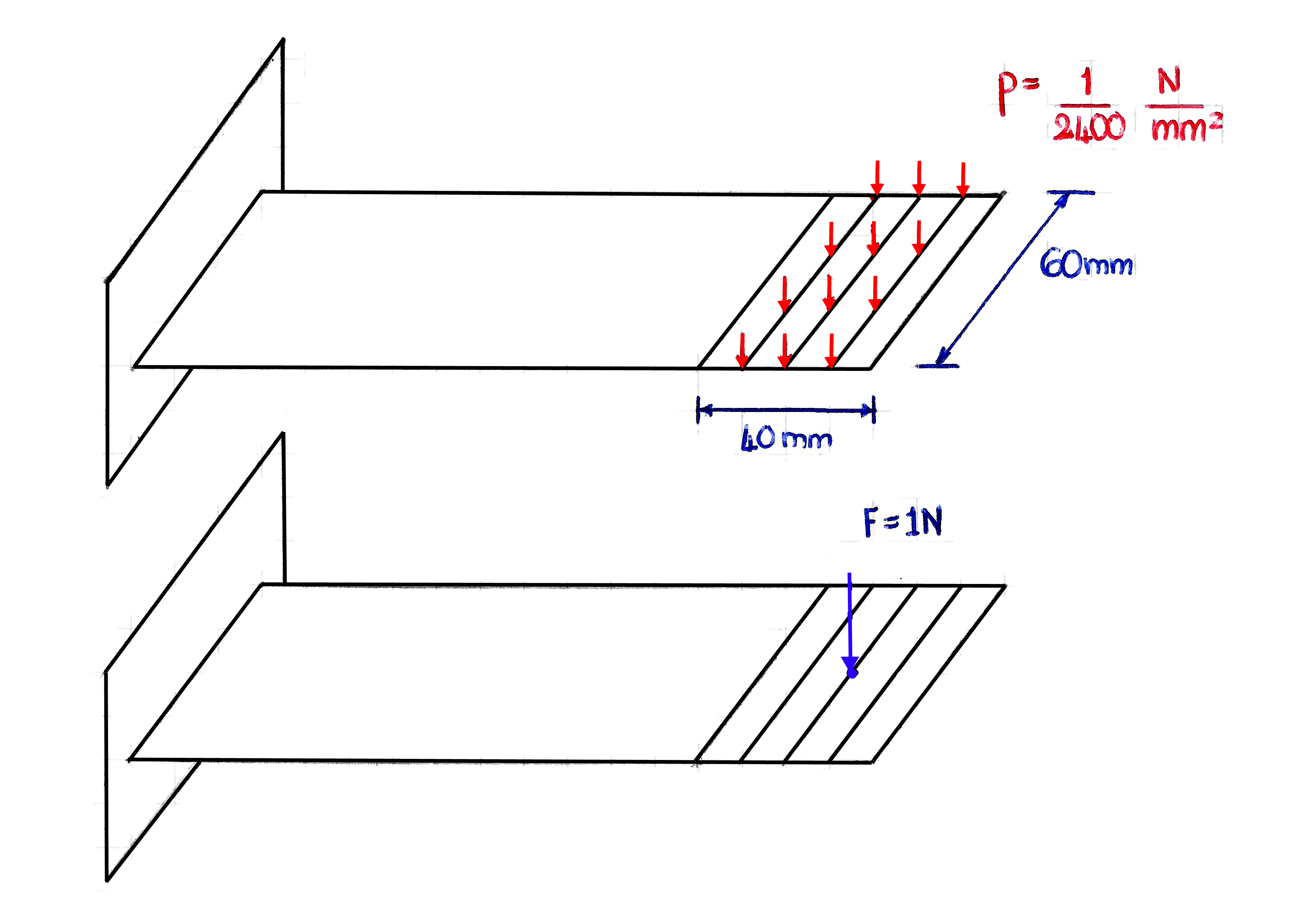
L’obiettivo della lezione di oggi è determinare la risposta della struttura sia a sollecitazione statica che armonica modulata. L’idea è quella di applicare una pressione tale per cui la risultante della distribuzione è una forza F di 1 N applicata al baricentro dell’area delle prime quattro file di elementi della lamella, cioè una quantità di 40×60 mm nel verso di x positivo.
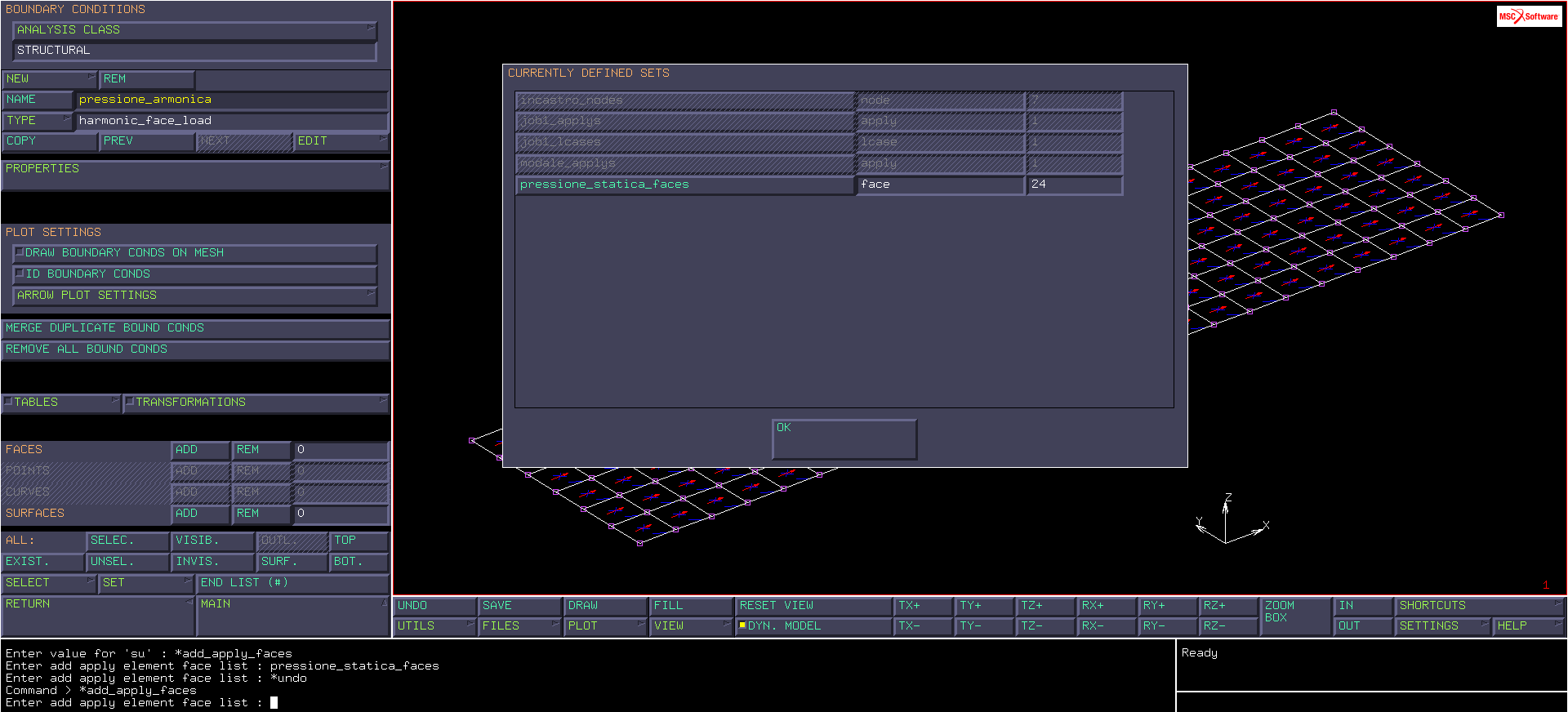
L’area su cui è applicata la pressione è 60×40=2400 mm2; il baricentro della distribuzione è un nodo ed è il punto di applicazione della risultante. Per imporre la pressione sulle facce della lamella (se non attivate, per visualizzare le facce, selezionare della voce PLOT i comandi ELEMENTS>SETTINGS>REGEN) dobbiamo creare la prima boundary condition (“pressione_statica”) dal menu BOUNDARY CONDITIONS>NEW>STRUCTURAL>FACE LOAD e successivamente, cliccando su PROPERTIES attivare la voce PRESSURE e assegnare il valore 1/2400. Per applicare questa BC basta cliccare su FACES ADD, selezionare le facce di interesse (ricordandosi di disattivare il DYNAMIC MODEL) e dare il comando END LIST.
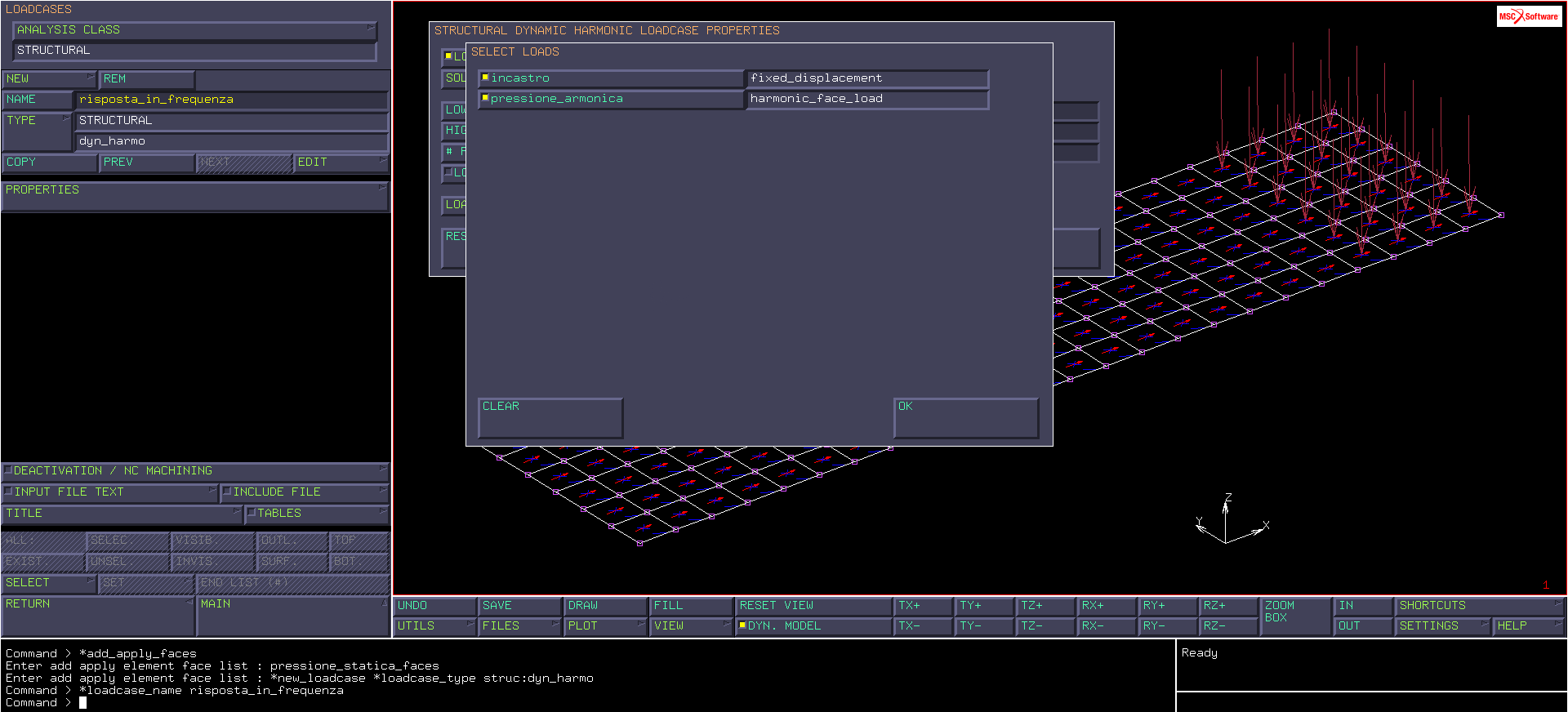
Allo stesso modo creiamo la seconda boundary condition (“pressione_armonica”) dal menu BOUNDARY CONDITIONS>NEW>STRUCTURAL>HARMONIC FACE LOAD, definendola tramite intensità e fase cliccando su PROPERTIES e selezionando MAGNITUDE & PHASE dalla voce INPUT MODE. Per impostare i valori di intensità e fase attiviamo la voce PRESSURE (sempre nel menu PROPERTIES) e diamo anche qui come valore 1/2400 per MAGNITUDE, lasciando il valore di PHASE pari a 0. Per aggiungere le facce, oltre al procedimento classico con FACES ADD, si può utilizzare il comando FACES ADD>SET, selezionando il set di facce già utilizzato per la pressione statica.
È necessario, ora, definire il range di frequenze ω (o pulsazioni 2πω) sul quale modulare la sollecitazione; creiamo un nuovo loadcase di tipo strutturale (che chiameremo “risposta_in_frequenza”) dal menu LOADCASES>NEW>DYNAMIC HARMONIC. Cliccando su PROPERTIES inseriamo i seguenti valori: LOWEST FREQUENCY=1, HIGHEST FREQUENCY=600 e FREQUENCIES=1199. Per la frequenza massima è stato scelto un valore intermedio fra terza e quarta frequenza propria riferendo la nostra analisi solo ai primi tre modi propri, mentre il valore degli steps è stato scelto in modo da avere un campionamento ogni 0.5 Hz.
Cliccando successivamente su LOADS (sempre nel menu PROPERTIES), attiviamo sia “incastro” che “pressione_armonica”.
Per ogni campionamento viene risolto il sistema [1]: nelle ipotesi fatte, cioè in assenza di smorzamento e non introducendo fasi sulla sollecitazione, la risposta sarà reale.
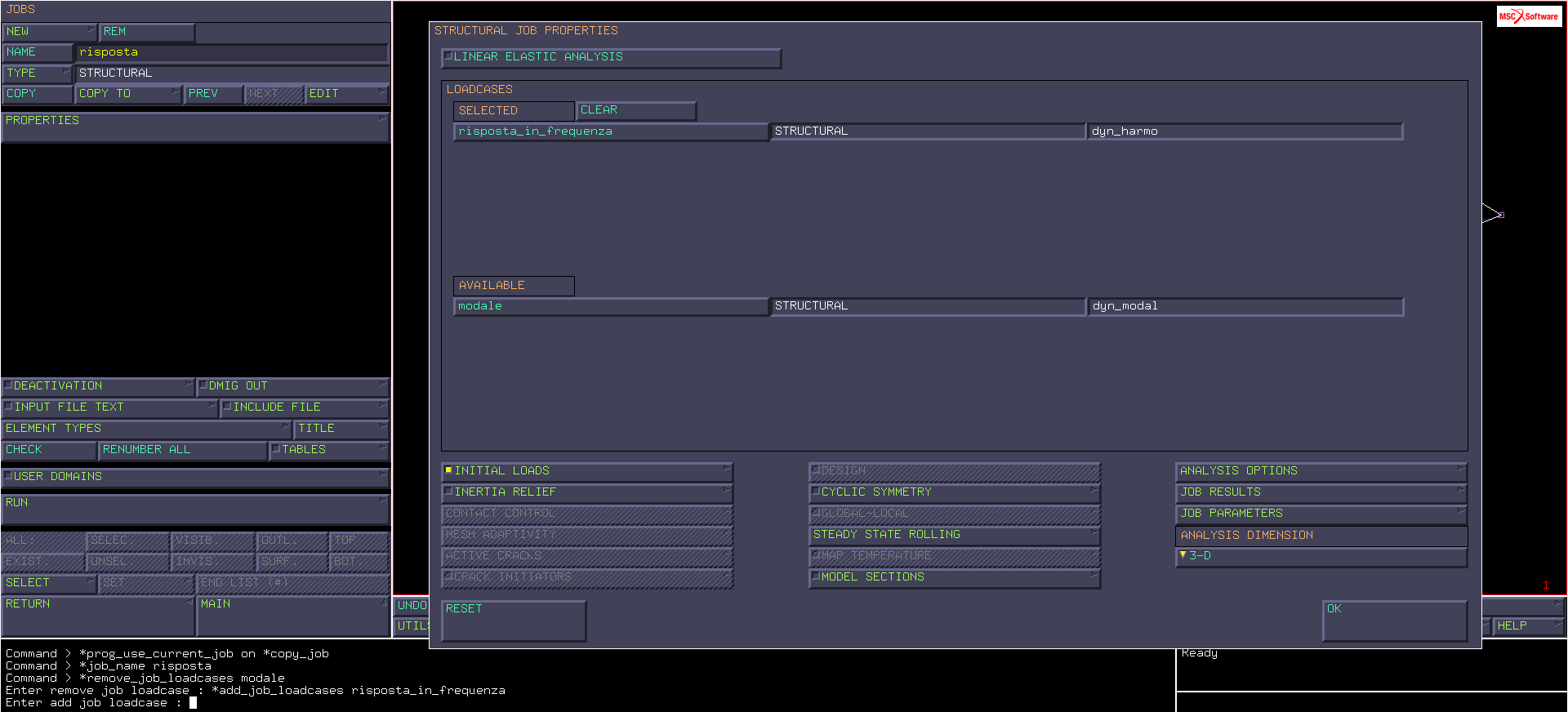
Procediamo alla creazione di un secondo job (il primo è quello creato la settimana scorsa e che rinomino “modale”): invece di creare un nuovo job da zero, dato che i risultati che ci interessano sono sempre gli stessi, clicchiamo su COPY per creare un job2 identico al job “modale” e lo rinominiamo “risposta”. Dal menu PROPERTIES, deselezioniamo il loadcase “modale” e attiviamo quello “risposta_in_frequenza“.
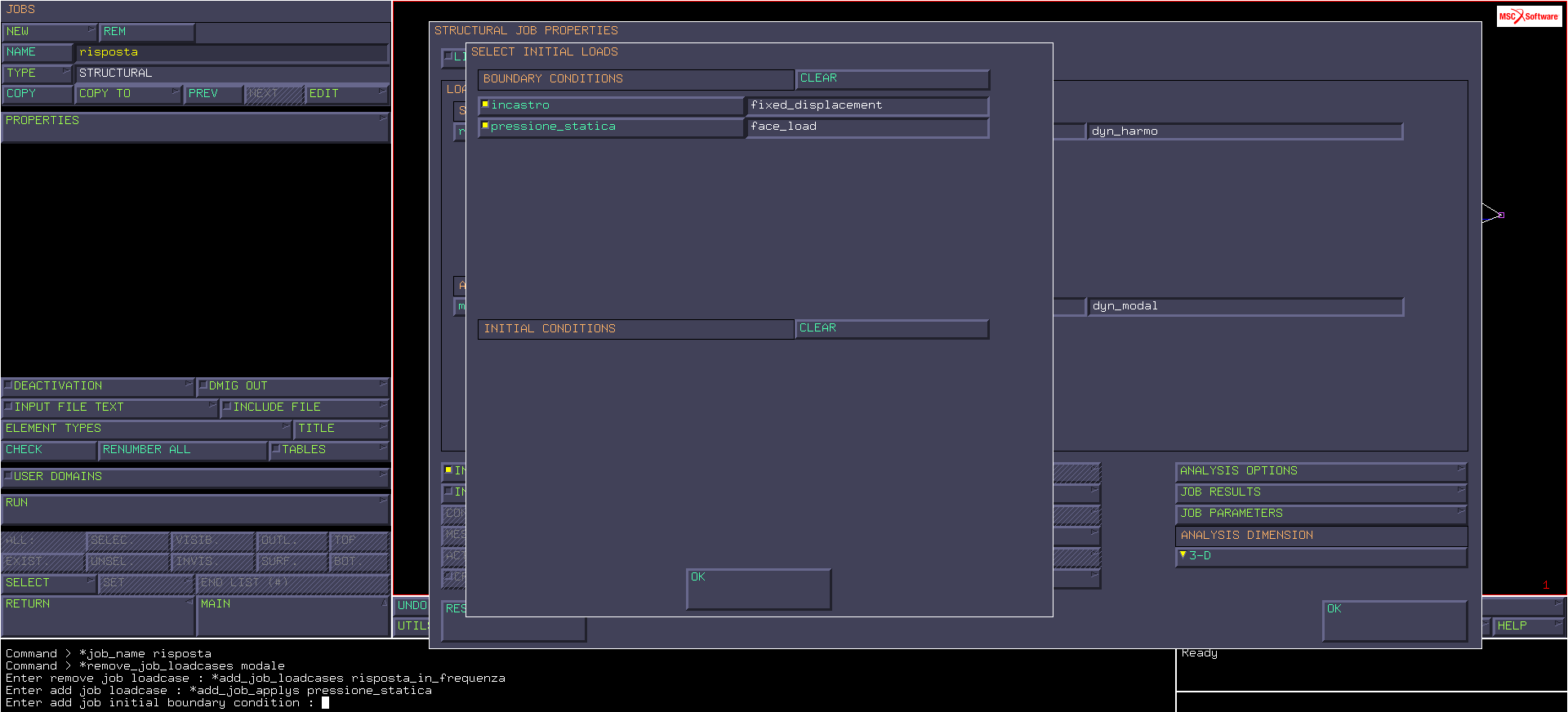
Dal menu INITIAL LOADS definiamo i carichi all’incremento zero, selezionando “incastro” e “pressione_statica”.
In generale, si inserisce come carico all’incremento zero solo ciò che serve per le definizioni di matrice di rigidezza e matrice di massa; in questo caso è possibile utilizzarlo anche come analisi statica, perché la pressione non modifica la matrice di rigidezza. Intendiamo quindi lo step zero come la risposta del sistema alla pressione statica.
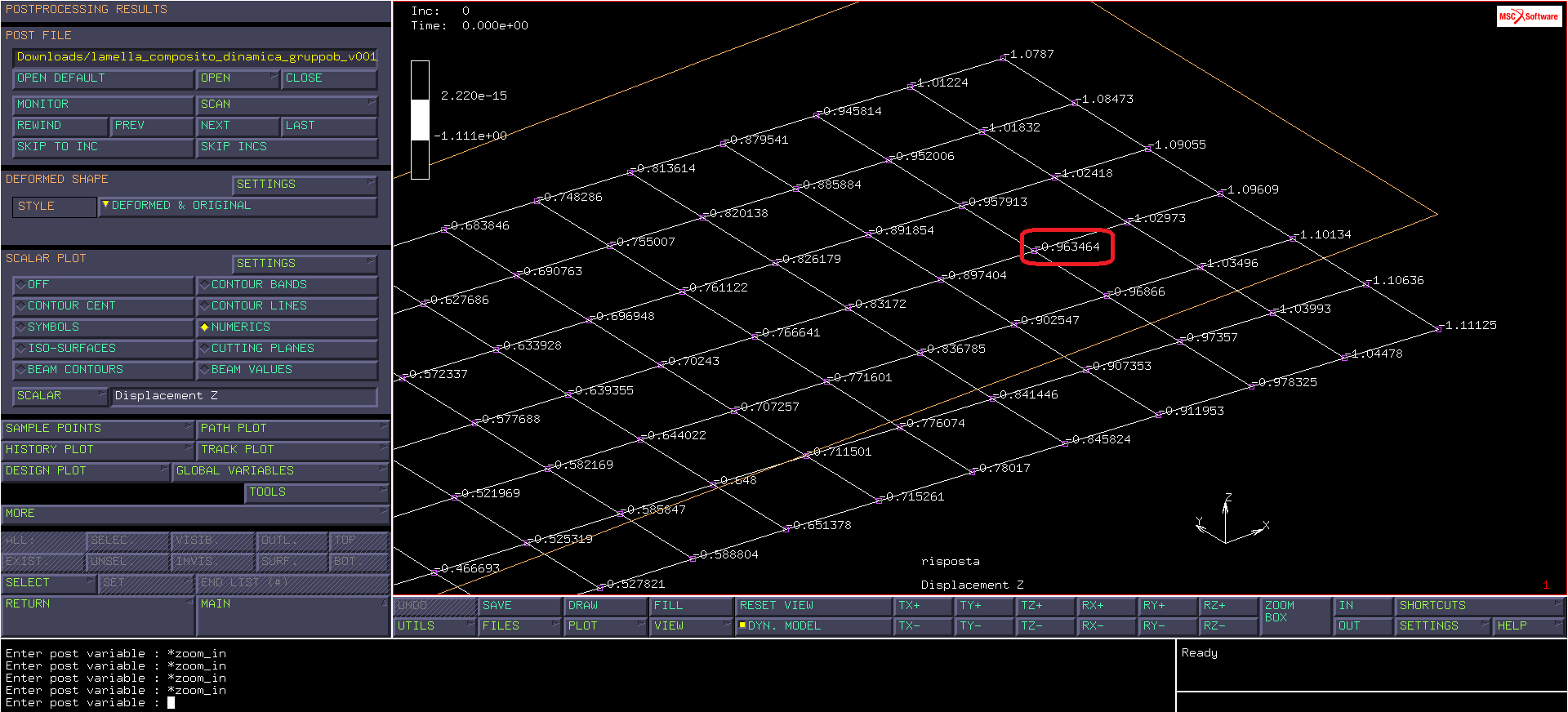
Mandiamo in esecuzione con JOBS>RUN>SUBMIT e, appena finisce di elaborare, apriamo il file dei risultati (OPEN POST FILE). Facendo attenzione ad impostare “deformed & original”, alla voce “style”, e a impostare una scala opportuna, si vede la differenza tra la configurazione originale e quella deformata. Dal menu SCALAR PLOT selezioniamo “contour bands” e “displacement z” (dal sottomenu SCALAR) per monitorare lo spostamento lungo z normale al piano della lamella.
Si nota come lo spostamento non sia simmetrico (a causa della laminazione): se lo fosse, le curve di livello sarebbero rette perpendicolari all’asse x.
Passando da “contour bands” a “numerics”, è possibile visualizzare lo spostamento del baricentro della distribuzione che ha un valore di 0.963464 mm.
Cliccando su “next”, possiamo vedere la prima risposta in frequenza, ovvero la risposta della struttura sotto la pressione modulata ad 1 Hz. In questo caso, lo spostamento del baricentro è di 0.963981 mm: la risposta nel caso statico e quella alla frequenza di 1 Hz sono diverse alla quarta cifra decimale, pertanto la soluzione statica è ingegneristicamente utilizzabile anche ad oscillazioni a bassa frequenza (frequenza molto più piccola della prima frequenza propria).
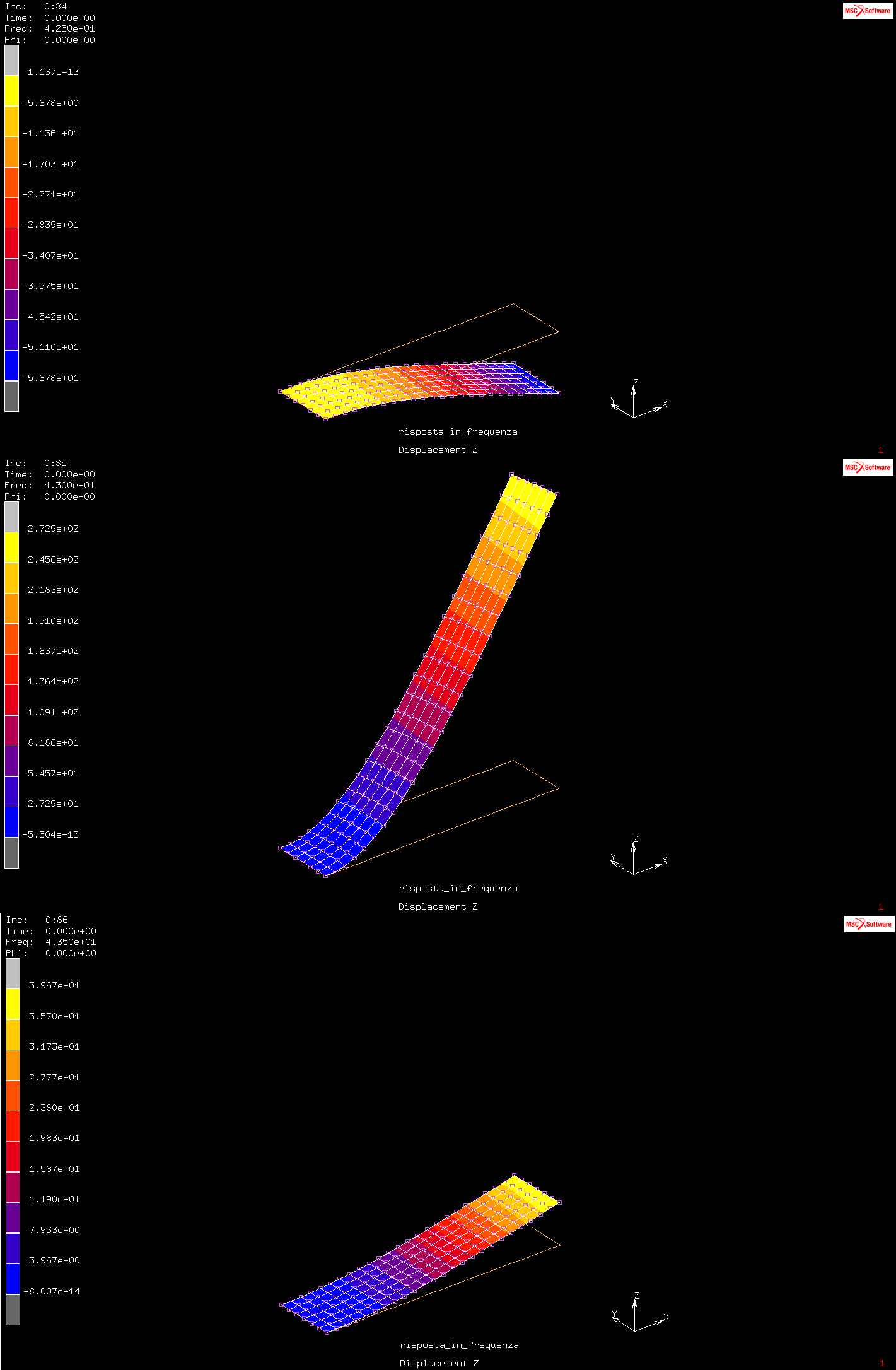
Continuando a cliccare su “next” notiamo che fra 42.5 e 43 Hz è presente un’anomalia nella risposta (più precisamente è 42,91 Hz, come si vede dalla tabella in alto). Analizzando la risposta notiamo che l’ampiezza aumenta avvicinandoci alla risonanza, diventa più elevata nei due campionamenti subito prima e subito dopo la risonanza (42.5 e 43 Hz), poi diminuisce: la risposta immediatamente prima della frequenza propria ha fase 0, cioè è in fase con la sollecitazione eccitante; oltrepassata la risonanza, la fase passa da 0 a π, e quindi la risposta risulta in controfase con la sollecitazione. A fase 0 la pressione e lo spostamento sono verso il basso, dopo la risonanza la pressione è verso il basso, mentre lo spostamento è verso l’alto, sempre nell’ipotesi di assenza di smorzamento.
Un fenomeno analogo si verifica per le altre frequenze di risonanza analizzate.
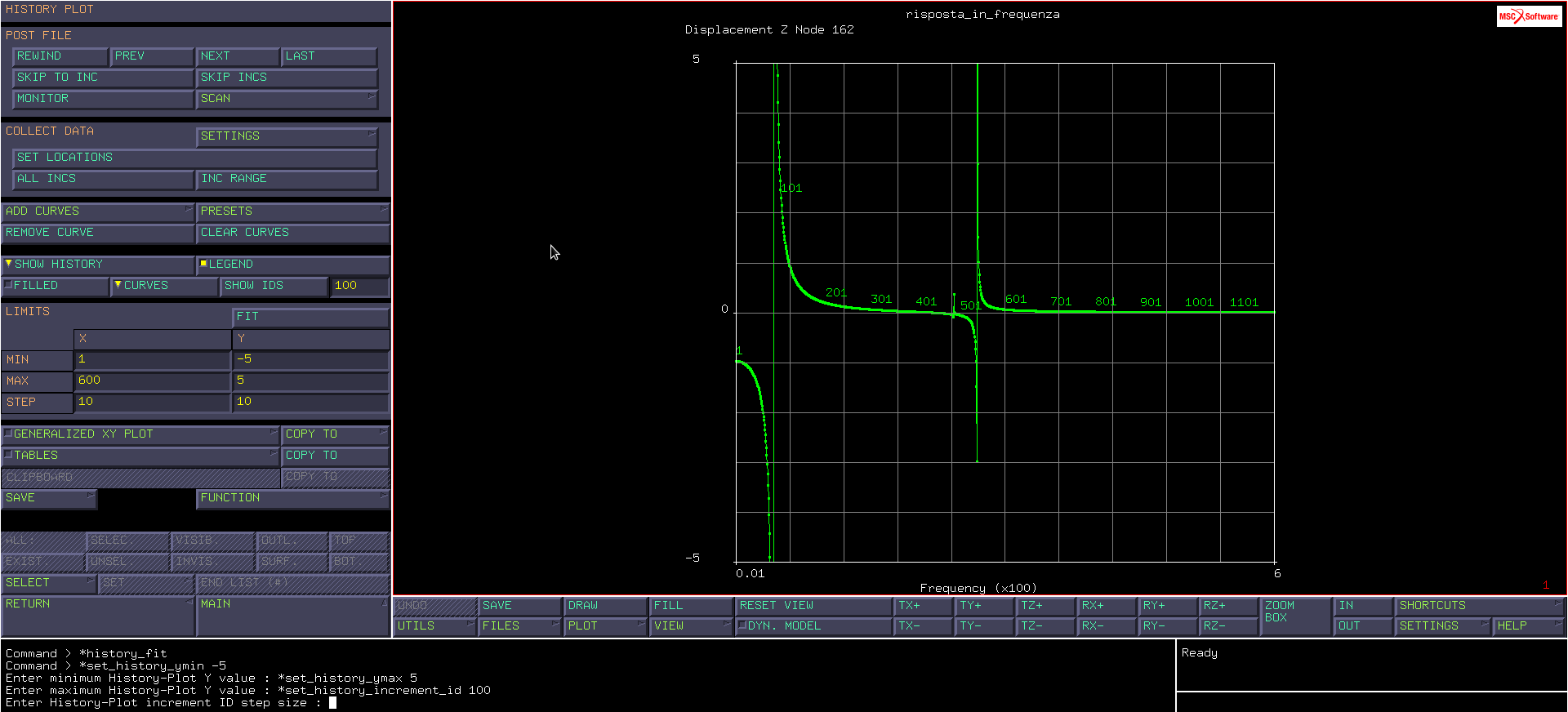
Creiamo, adesso, il grafico della risposta in frequenza relativo allo spostamento lungo z del baricentro: per selezionare il baricentro utilizziamo POSTPROCESSING>RESULTS>HISTORY PLOT>SET LOCATION, selezioniamo il nodo baricentrico e diamo END LIST. A questo punto bisogna estrarre i dati raccolti dal nodo su un range di incrementi, attraverso INC RANGE; nella barra dei comandi in basso, alla voce “Enter first history increment” inserire “0:1”, alla voce “Enter last history increment” inserire “0:1000000”, alla voce “Enter increment step size” inserire “1”: in questo modo il grafico partirà dal sottoincremento 1 dell’incremento 0 e arriverà al sottoincremento 1000000 dell’incremento 0 con passo 1; è stato utilizzato come ultimo incremento un valore irragionevolmente grande per avere la certezza di coprire tutti gli incrementi, laddove non ci si ricordi il numero esatto di incrementi scelti.
Per estrarre il grafico, sempre nel menu HISTORY PLOT, si utilizza il comando ADD CURVES>ALL LOCATIONS (poiché abbiamo solo il grafico riferito al baricentro); a questo punto nella barra dei comandi vengono richieste le variabili X e Y: alla voce “Enter x-axis variable” selezionare nel menu GLOBAL VARIABLES la voce FREQUENCY, mentre per “Enter y-axis variable”, dal menu VARIABLES AT LOCATIONS, selezionare DISPLACEMENT Z. Per plottare il grafico utilizzare il comando FIT.
Impostando arbitrariamente ed adeguatamente i valori massimo e minimo dell’asse y, si vede che il grafico ha due picchi, relativi al primo e al terzo modo proprio, molto più elevati rispetto a un terzo picco (situato fra i due precedenti), relativo al secondo modo proprio. In realtà i tre picchi sono esattamente equivalenti e tutti e tre assumono valore pari a infinito poiché si trovano in corrispondenza di tre frequenze di risonanza della lamella: i diversi valori visualizzati nel grafico (compreso quello del picco “più alto” pari a 491,4 mm) sono solo da attribuirsi al numero di campionamenti fatti e alla loro distanza dalle frequenze di risonanza.
L’analisi si ritiene quantitativamente esatta ovunque, a meno delle risonanze. Per avere informazioni realistiche sulle risonanze occorrerebbe introdurre lo smorzamento C in modo da non avere divergenza a +∞.
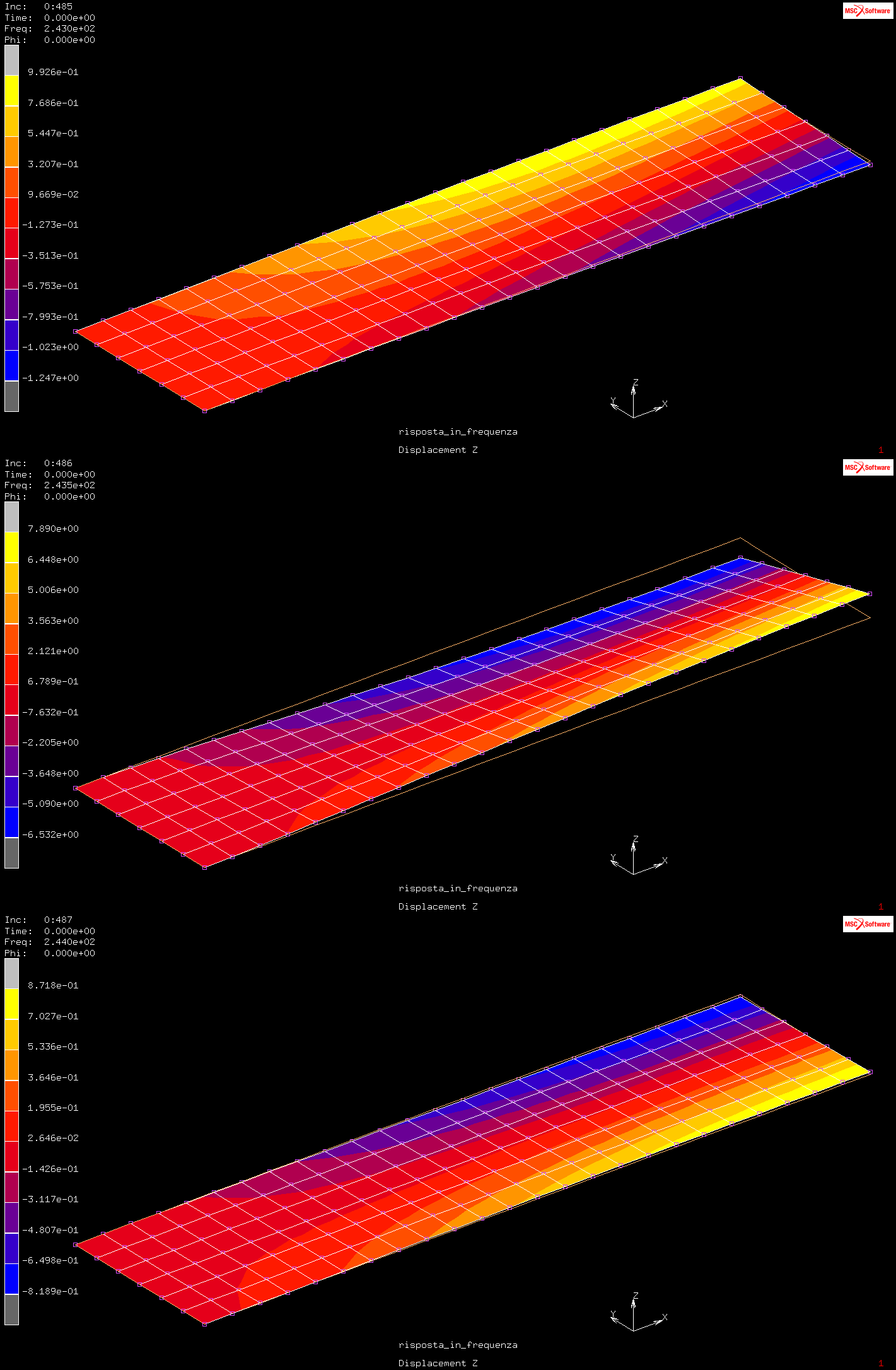
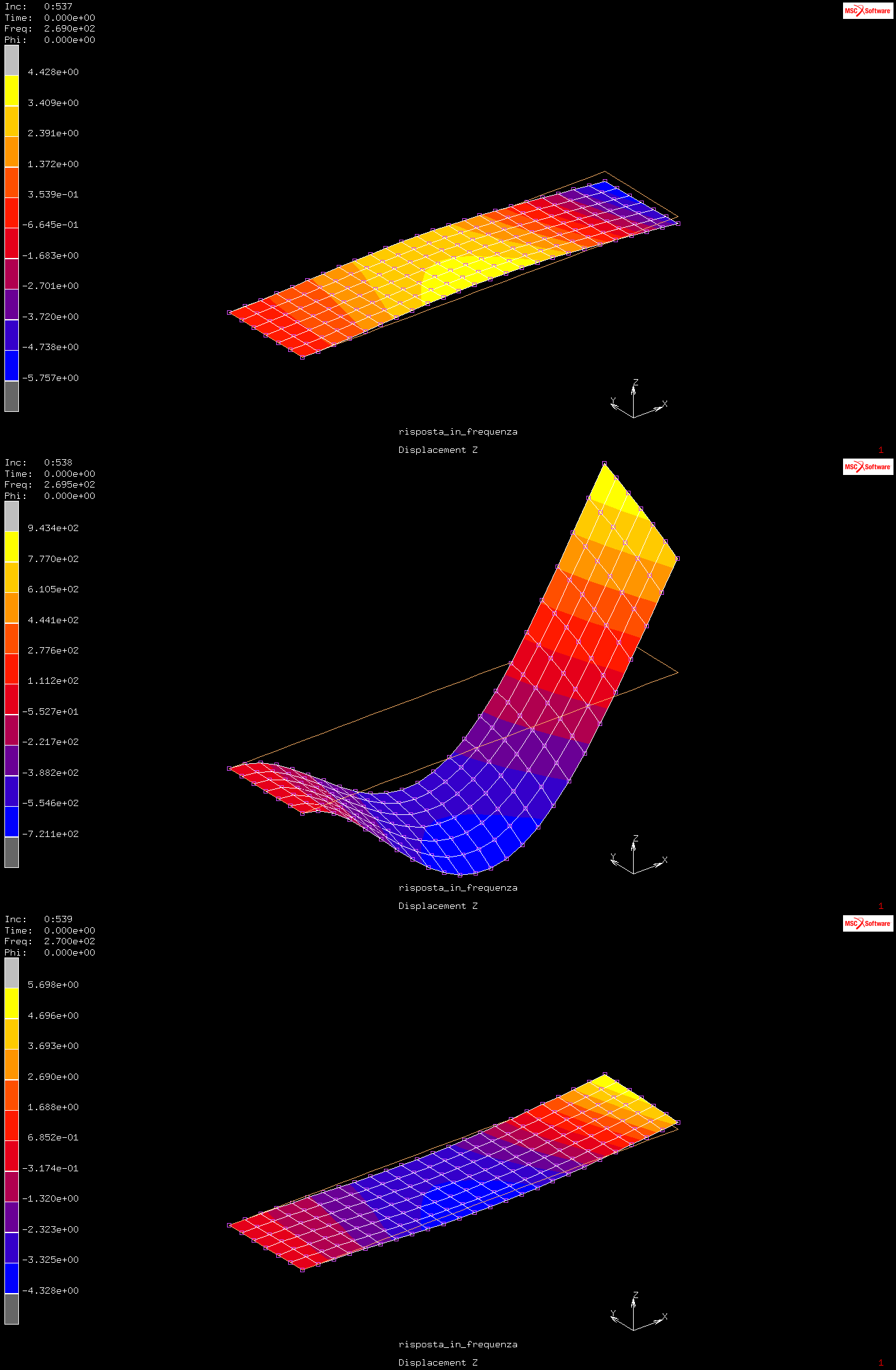
Per capire perché la seconda risonanza sembra meno critica delle altre due, andiamo ad analizzare nuovamente i modi propri: chiudiamo il file dei risultati e lanciamo nuovamente il job “modale” andando a visualizzare il ”Displacement Z”. Il primo e il terzo modo proprio presentano uno spostamento del baricentro abbastanza elevato, tale da giustificare i picchi più elevati presenti nel grafico.
Analizzando il secondo modo proprio notiamo come la potenza istantanea su metà della lamella sia opposta in segno rispetto a quella sull’altra metà (zona blu e zona gialla); se i valori in queste due zone fossero uguali e opposti avremmo una situazione di perfetta antisimmetria, ma dai valori nella scala a sinistra si vede che non è così: la pressione eccita il modo proprio solo per la quota parte relativa alla differenza fra questi due valori, per questo motivo lo spostamento del baricentro risulta di entità minore rispetto a quello degli altri due modi propri.