Indice
DINAMICA DELLE STRUTTURE
Apriamo con Marc Mentat il modello “telaio_monoscocca_v006b”
L'ultima volta avevamo applicato al nodo del pneumatico anteriore destro un carico in direzione y di 1N, in forma statica equilibrato dalle forze inerziali di un'accelerazione uniforme nel tempo. ( moto uniformemente accelerato).
Oggi sul modello andremo a studiare i modi propri di questa struttura.
La soluzione trovata la scorsa volta è valida per il carico statico e sarà valida anche per le basse frequenze nel caso modale. Nel senso che le oscillazioni in bassa frequenza, consapevoli di ammettere un errore piccolo, saranno valide anche per il caso statico finchè la frequenza di modulazione sarà meno della metà della prima frequenza propria del sistema (frequenza di risonanza). Se ci vengono chiesti margini di errore molto più stretti la soluzione statica sarà buona solo per frequenze molto più basse (0,01 Hz).
Ai fini di definire la validità della soluzione statica andremo ad estrarre la prima frequenza propria della struttura.
Vado in Marc.
- Main → Loadcases → new → dynamic modal → name: Modale
- Properties → low frequency: 1Hz → #modes: 10
Proprietà : E' una modale che voglio fare con le stesse condizioni di vincolo del caso statico (in assenza di vincoli). Avrò un sistema non vincolato. So a priori che i primi 6 modi propri della struttura saranno a 0 Hz e rappresentano i 6 moti di corpo rigido e non li voglio considerare (avrei problemi numerici con l'algoritmo di calcolo). Allora faccio partire l'analisi da 1 Hz (scelgo 1 Hz perché è una frequenza abbastanza bassa per le strutture meccaniche) e valuto 10 modi proprio a partire da 1 Hz.
Vado a selezionare anche l'opzione “Non-positive Definite” per avvertire il sistema che allo step 0 la matrice di rigidezza sarà singolare. Lo avverto per evitare l'errore 2004. (so a priori che è non vincolato e quindi labile).
Creo il JOB:
- Main→job→new→strutural→name: Modale
- →proprieties→ initial load→ lascio attiva solo la massa di campionamento (1mg) (la struttura sarà scarica e svincolata)
Detto ciò avvio seleziono il loadcase appena creato e avvio il calcolo attraverso RUN!
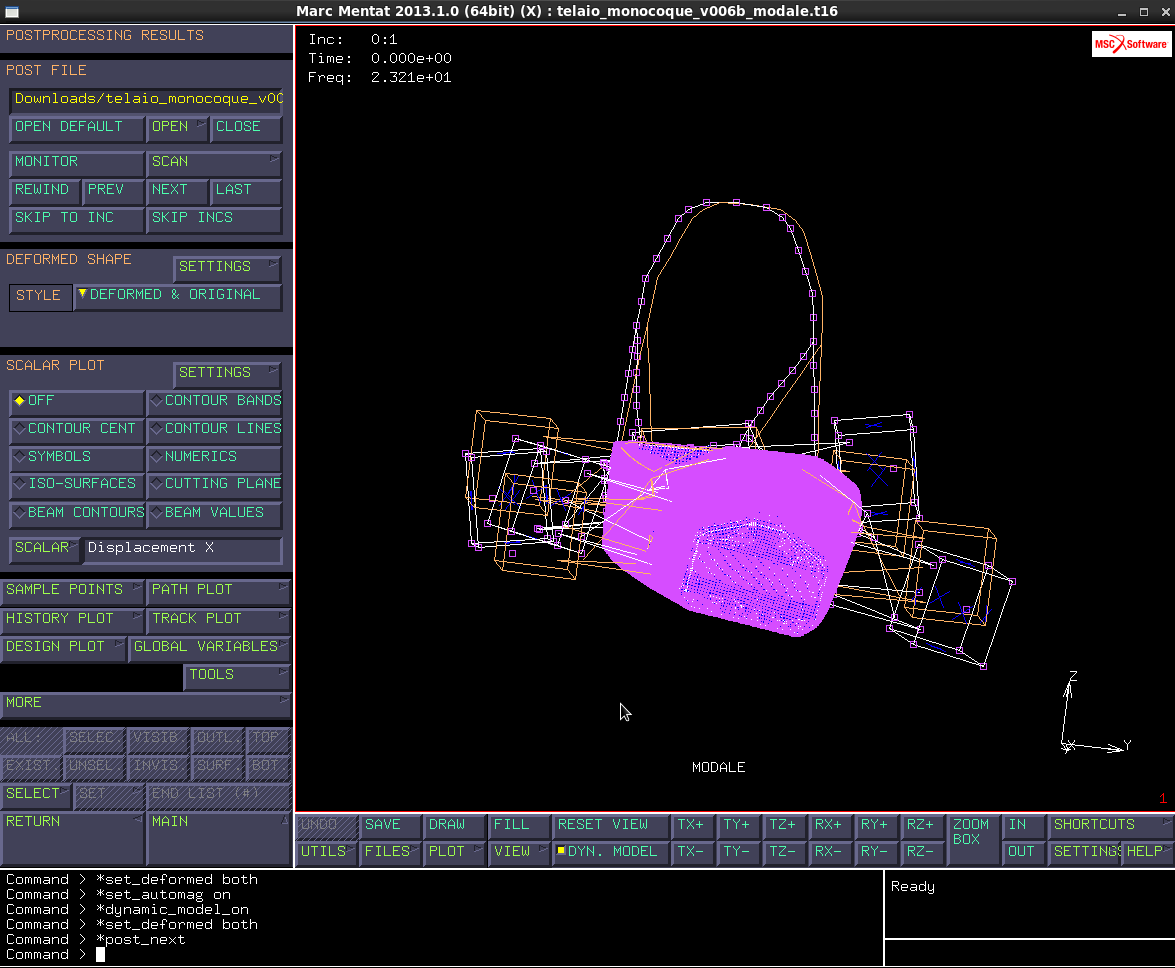
Con il comando submit→ Open post file results→next. Ora estraggo i primi modi propri:
Notiamo che il primo modo è alla frequenza di 23.21 Hz e andando ad analizzare la deformata notiamo che la nostra struttura subisce una torsione lungo l'asse longitudinale (l'assale posteriore tende a controrotaie rispetto all'assale anteriore). Il primo modo proprio è di tipo torsionale.
Il secondo modo proprio a 49,51Hz invece causa questa deformata:
Il secondo modo proprio causa solamente uno sterzamento della ruote anteriori. Perché? Cosa succede?
Vediamo in dettaglio, andando a nascondere i nodi per una visione più chiara in modo da lasciare in vista solo gli edges ( profili ) e valuto gli spostamenti in z. (displacemenet Z).
Mi rendo conto che il moto prevede una sterzatura delle ruote anteriori e una deformazione a S della parete inferiore del monoscocca. Alcuni punti vanno verso l'alto e altri verso il basso. Ma come è attaccata la scatola sterzo?
Vediamo che in quei punti è attaccata la scatola dello sterzo. Questo modo priorio è un modo proprio indotto da una scarsa rigidezza dei punti di attacco della scatola sterzo. La scatola sterzo probabilmente si appoggia su una zona non rinforzata del monoscocca: i punti di attacco sono troppo vicini e quindi il risultato è quella deformazione. Questo causerebbe vibrazioni del volante nel momento in cui il pilota affrontasse un manto stradale sconnesso.
La problematica si può correggere andando a rinforzare la piastra inferiore del monoscocca in corrispondenza dell'attacco della scatola sterzo oppure la scatola sterzo la si modifica e la si collega ad un telaietto alle pareti laterali del monoscocca.
I successivi modi propri vanno a coinvolgere il roll bar e le masse posteriori. Il terzo è a 64 Hz, poi il quarto coinvolge solo il roll bar sul fianco a 68 Hz. In questo caso potremmo installare una traversa in prossimità del roll-bar per irrigidire quella porzione di telaio.
Primo modo
Andiamo ora a concentrarci sul primo modo proprio (a 23,21 Hz). Ci interessa affrontare questa analisi per valutare le inertanze del telaio nel punto di appoggio a terra della ruota destra in termini di carico laterale. Valutiamo le Inertanze per esempio da 0 a 100 Hz (a causa di qualche motivo regolamentare della configurazone dell'auto pre-gara.)
Voglio campionare allora la risposta della struttura da 0 a 100 Hz. In assenza di smorzamento l'inertanza della struttura ha una frequenza pari a quella del primo modo proprio. So già a priori cosa succede sulla risonanza, avrò una risposta infinita in assenza di smorzamento. Se introduco uno smorzamento la risposta sarà funzione dello smorzamento introdotto.
Voglio valutare la risposta del sistema in un range di frequenze prossime a quelle di risonanza. Valuto da 21 Hz a 25 Hz con un passo di 0.1 Hz ( 40 step )
Suppongo di prendere quel N applicato staticamente e di applicarlo in forma armonica con fase nulla modulata in frequenza da 21 a 25 Hz con passo 0.1 HZ
Impostiamo l'analisi:
- Menù→ Boundary Conditions → copio la BC “carico_1N_y” che era statico e ne facciamo una variante dinamica e creiamo un carico che chiamiamo “carico_1N_y_armonico”. Basta cambiare il tipo di carico.
- Type→ Structural → da point load lo metto armonic point load, a questo punto:
- Proprierties→ force y→ magnitude:1
Definito l'armonic point load vado in:
- Loadcases → New → Dynamic Armonic → name: “ Risposta prima risonanza “
- Proprierties: *lowest frequency: 21 *highest frequency: 25 *frequency : #40
- Loads: nessun vincolo! solo il carico di 1N in y armonico ( 1N_Y_armonico )→ok→save.
Creiamo il JOB:
- Jobs → New → Structural → nome: ”“Risposta” → Proprieties → Initial Load scarico (stato iniziale scarico e svincolato).
Aggiungo degli output
- Job Results:
-Equivalent Von Mises stress: questa è statica, non verrebbe usata in un calcolo armonico, allora dato che lo stato tensionale oscilla in maniera armonica e la tensione equivalente non oscilla in forma armonica perché non è lineare con le tensioni, nel dubbio aggiungo:
-Equivalent Real Armonic Stress : è la Von Mises in fase 0 rad e $\pi$ rad del mio ciclo di oscillazione.
-Equivalent Imaginary Armonic Stress : è la tensione equivalente a fase $\frac{1}{2} \pi$ e $\frac{3}{2} \pi$ del mio ciclo di oscillazione.
- →save→ run→submit.
PREDIZIONE DI STATI DI INSTABILITA' IN STRUTTURE ELASTICHE DISCRETIZZATE FEM
Quando si parla di strutture leggere, si parla di strutture snelle e solitamente le strutture snelle hanno problemi di stabilità
INSTABILITA' EULERIANA
Tratta l'impossibilità di rompere a compressione una trave snella soggetta a carico assiale in quanto si rompe a flessione.
Trave con rigidezza flessionale EJ e lunghezza L.
Se analizzo l'elemento con una FEM la risposta è una e una sola e l'oggetto va in compressione se rimaniamo nel campo elastico-lineare. La soluzione in elasticità lineare è unica ed è quella compressiva. Ma qualcosa va storto nelle ipotesi che utilizziamo per fare l'analisi, va storto il concetto di elasticità lineare. Devo introdurre una non linearità onde evitare che l'oggetto vada sempre in compressione. La non-linearità che devo introdurre viene introdotta in quanto in teoria vado a considerare l'equilibrio della struttura non nella sua configurazione indeformata ma considero l'equilibrio nella sua configurazione DEFORMATA allora suppongo che ci sia una configurazione deformata.
Applico il carico e vado a considerare l'equilibrio su ognuno dei conci di trave deformato ed arrivo ad un equazione differenziale del secondo ordine da cui valgono i risultati seguenti:
Dall'analisi dell'equazione differenziale del secondo ordine risulta che la soluzione compressiva è l'unica ammessa se:
P < Pcritico → ho solo soluzione compressiva (ossia quella in continuità con i piccoli carichi).
Analizziamo su un grafico il carico P e la deformazione \delta .
La retta è composta da punti che determinano uno stato di equilibrio per ogni diverso carico. La linearità esiste finchè il carico è minore del Pcritico.
\[P= \frac{\pi^{2}\cdot EJ}{ L^{2}}\]
Se P=Pcritico la soluzione compressiva non è più l'unica, ma alla soluzione del problema si aggiunge un moto di deflessione di forma sinusoidale.
Funzione sinusoidale: \[f(x) =a\cdot sen(\frac{x}{L} \cdot \pi )\]
Analizziamo ora l'andamento del carico P in funzione dell'ampiezza della sinusoide a.
Se P < Pcritico → a=0 ( la soluzione ammessa è solo quella compressiva ) Se P = Pcritico a può sussistere in valore arbitrario
Quando raggiungo il Pcritico muovendomi dall'origine lungo la retta, devo aggiungere a questo stato di equilibrio il contributo sinusoidale
A fronte di una variazione di P ho una variazione di spostamenti.
Ma posso avere una perturbazione di spostamenti senza spostare il carico e trovarmi ancora in equilibrio. Spostandomi sulla retta parallela ad a posso variare la forma della struttura senza variare il carico. Mentre il punto di applicazione della forza ( /delta) non varia.
Esistono diversi tipi di equilibrio, esso può essere: stabile, instabile o indifferente.
Per verificare la stabilità di quell'equilibrio devo andare a calcolare l'energia potenziale totale ( elastica + en potenziale dei carichi che suppongo conservativi e quindi che ammettono potenziale)
La stabilità di un equilibrio passa per la valutazione dell'energia potenziale. Gli equilibri sono tutti punti stazionari dell'energia potenziale. L'equilibrio è stabile se un punto stazionario è di minimo, instabile se il punto stazionario è un massimo, equilibrio indifferente se è un punto di sella. Mi serve una funzione potenziale ( energia potenziale elastica + energia potenziale dei carichi che devono ammettere potenziale, quindi che devono essere conservativi)
Quando un carico non è conservativo? Quando ad esempio considerando un’asta inflessa il carico rimane solidale con l’estremo dell’asta, quindi una trave con una forza che segue la sua orientazione, oppure una pressione.
Le nostre travi hanno un potenziale, il carico rimane fisso come orientazione nello spazio ed è indipendente da come si muove il punto di applicazione
Quando ci sarà il punto critico? Suppongo di muovermi sulla soluzione di elasticità lineare e mi chiedo quando questa soluzione non sarà più l’unica(molteplicità della soluzione). Il punto è critico non per la struttura che potrebbe anche reggere ma perché va in crisi la soluzione lineare. Poniamoci ora in un caso, diverso dalla trave snella precedente caricata in punta, il peggiore che si può incontrare.
Enuncio un metodo per predire la crisi delle soluzioni ottenute in prossimità dello stato critico (questo metodo funzione quasi sempre tranne in questo caso). Bisogna capire perché non funziona Il sistema considerato è caricato da una forza F e il grado di libertà che monitoro è lo spostamento $\delta$ del punto di applicazione (non monitoro il secondo grado di libertà che è lo spostamento laterale).
Considero ora la curva carico-spostamento per questo oggetto. La non linearità del sistema mi dice che a un certo punto devo trovare un massimo perché quando carico le molle fino ad allinearle non sono più in grado di reggere nessun carico verticale (perchè il carico è normale all’asse di molla). se aumento lo spostamento ottengo una curva simmetrica a quella di prima.
Le molle sono lineari, qual’è la non linearità di questa struttura?
La non linearità della struttura è data dal fatto che le molle ruotano di angoli non piccoli(fino a 45°),quindi di tipo geometrico. Quando ho grandi rotazioni va in crisi la forma linearizzata delle formule trigonometriche, non possiamo più dire che sin$\theta \approx \theta$ per $\theta = 45°$. Nei codici fem per studiare l’instabilità devo inserire una non linearità di tipo geometrico. Come procedo? Posso impostare un calcolo non lineare ponendo al posto della forza un carrello che farò scendere come nelle prove dove si utilizzano macchine a controllo di spostamento (una macchina a controllo di carico non seguirebbe il comportamento post instabilità di un provino in strizione).
Divido quindi il mio incremento di spostamento in tanti piccoli punti di campionamento utilizzo una complessa procedura di Newton-Raphson (non svolto) e se tutto converge ottengo con grandi costi computazionali l’andamento della figura. Spesso la curva è troppo complessa da gestire ed il metodo non va sempre a buon fine. Serve quindi un metodo più robusto e più semplice da utilizzare.
Forma semplificata del metodo ( utilizzato da marc)
Si prende una curva di carico
Considero due diverse condizioni di carico: il livello di carico $F_{0}$ è in equilibrio con la configurazione $\delta_{0}$ e localmente la tangente ha entità $K_{0}$, tipicamente è lo stato scarico. Il secondo stato di equilibrio diverso dal primo: stato 1. $K_{1}$ diverso da $K_{0}$ per avere caso di non linearità. Cosa succede per carichi diversi da $F_{0}$ e $F_{1}$? Voglio dei carichi che siano estrapolazioni di $F_{0}$ e $F_{1}$. Definisco
$F^{\lambda }= F_{0}+(F_{1}-F_{O})*\lambda$
Faccio ipotesi semplificativa: la matrice di rigidezza varia come variano i carichi.
$K^{\lambda }= K_{0}+(K_{1}-K_{O})*\lambda$
Posso allora cercare di individuare il punto critico andando a chiedermi quando la rigidezza diventerà nulla. La matrice rigidezza è definita positiva quindi ha autovalori non nulli e quindi mi chiedo quando un autovalore diventa nullo.
$det(K_{0}+\lambda *(K_{1}-K_{0}))=0 \rightarrow \lambda _{i}$ (uno per ogni grado di libertà)
Quando \lambda è uguale a quello sopra la matrice di rigidezza è singolare. $K_{1}- K_{0}$ è la correzione di K dovuta all’applicazione del carico.
$\left [ K_{0}+\lambda _{i}(K_{1}-K_{0}) \right ]V=0$
Risolvendo questo problema agli autovalori e autovettori trovo dei fattori di scalatura critici dei carichi che aprono alla possibilità di biforcazioni della soluzione. La forma della soluzione è raccolta negli autovettori v che sono le variazioni di spostamento ammesse con variazione di carico nulle.
$F_{0}=0 \rightarrow F_{crit}=\lambda _{i} \cdot F_{1}$
Così riesco a prevedere l’insorgere di queste condizioni di instabilità riducendo il problema a un problema di estrazione degli autovettori e autovalori.
Risultati risposta in frequenza telaio
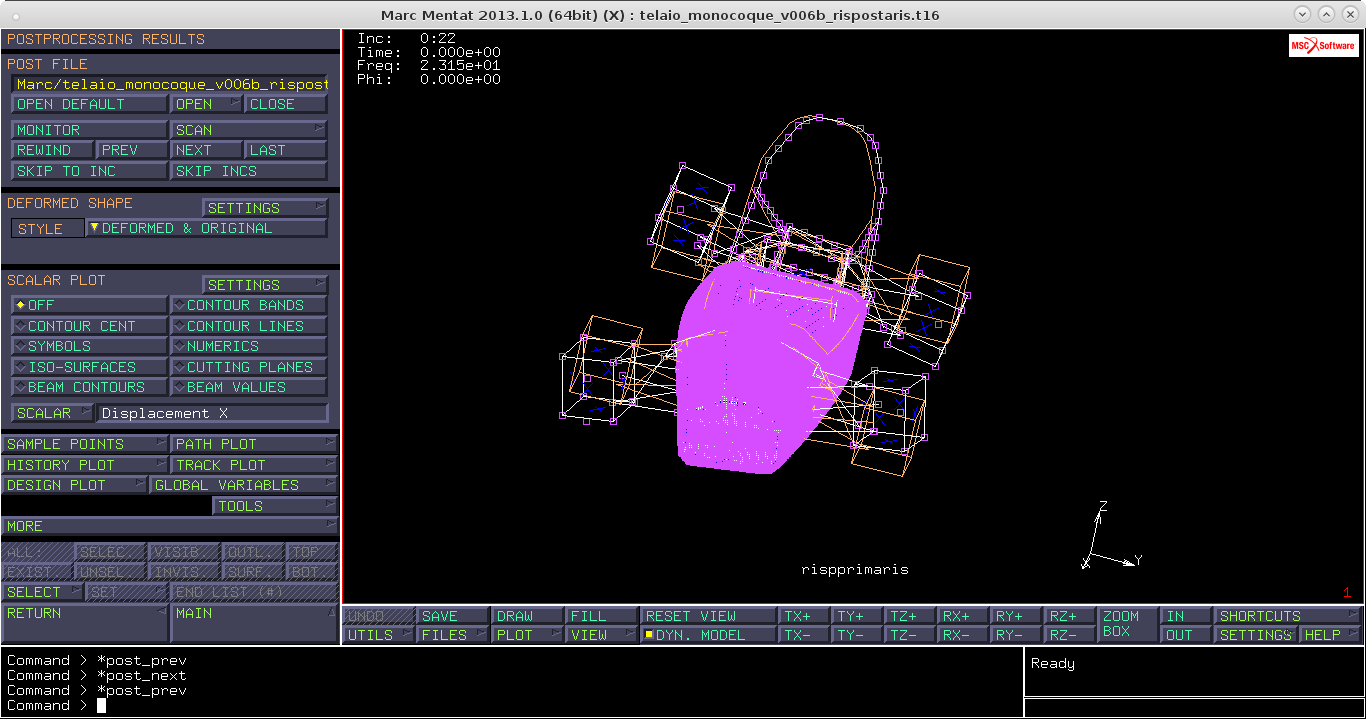
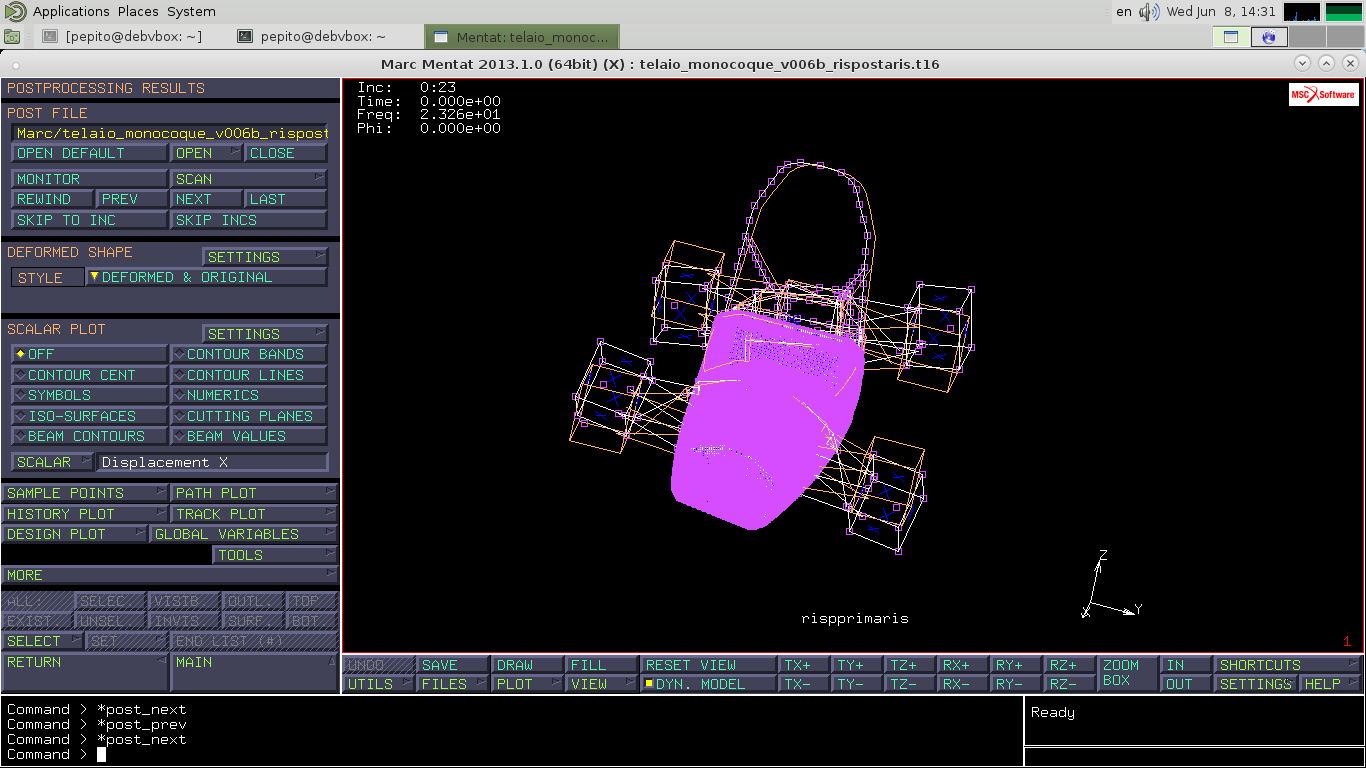
Torniamo alla valutazione della risposta in frequenza del telaio nell'intorno della prima frequenza di risonanza.
Apriamo il file dei risultati cliccando su Open post file Lo step 1 è la risposta a 21 Hz. Incrementando la frequenza noto che l'ampiezza di oscillazione cresce man mano che ci avviciniamo alla frequenza di risonanza. Mi accorgo di aver superato la risonanza per un rapido cambio di segno di tutti gli spostamenti poichè il comportamento pre-risonanza è in fase con la forza e quello post è in controfase (cambio di fase di %\pi%).
Ora andiamo a monitorare lo spostamento del nodo dove è applicata la forza, il centro dell'impronta a terra.
menù $\rightarrow $ set location $\rightarrow $ clicco sul nodo interessato $\rightarrow $ fine lista
inc range $\rightarrow $ nel terminal scrivo 0:1 (incremento iniziale (invio) $\rightarrow $ 0:100000 (esagero per essere sicuro di includere tutti gli incrementi) $\rightarrow $ 0:1 (passo del campionamento)
add curves $\rightarrow $ all locations $\rightarrow $ frequency, diplacement y
fit
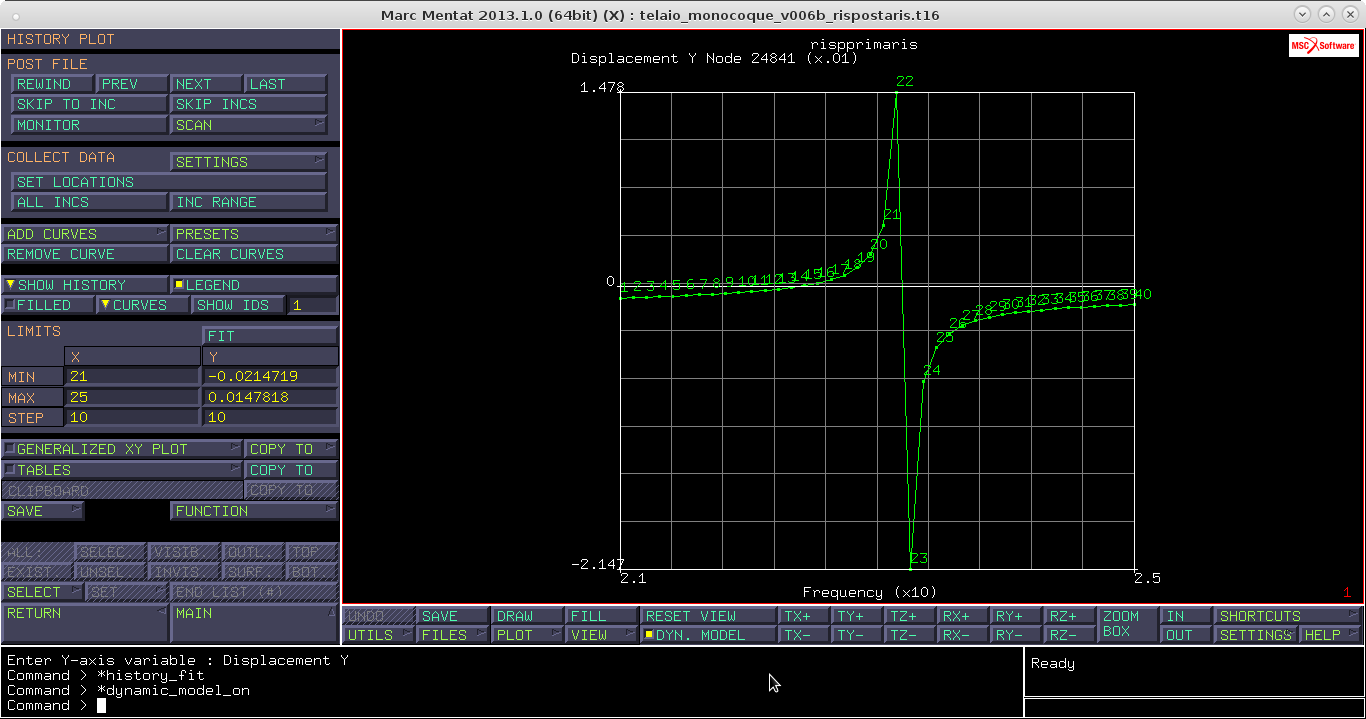
Ottenendo il grafico seguente.
I valori campionati come massimi non sono in realtà tali, perchè per definizione la risposta in risonanza di un sistema è $+\infty$. I valori massimi qui sono finiti per il fatto che i punti di campionamento generalmente non sono precisamente in corrispondenza della frequenza di risonanza. Per determinare l'inertanza basta moltiplicare la curva trovata per $\omega^{2} $. Chiudiamo il file di risultati e studiamo ora un problema di instabilità.
Instabilità di una struttura in Marc
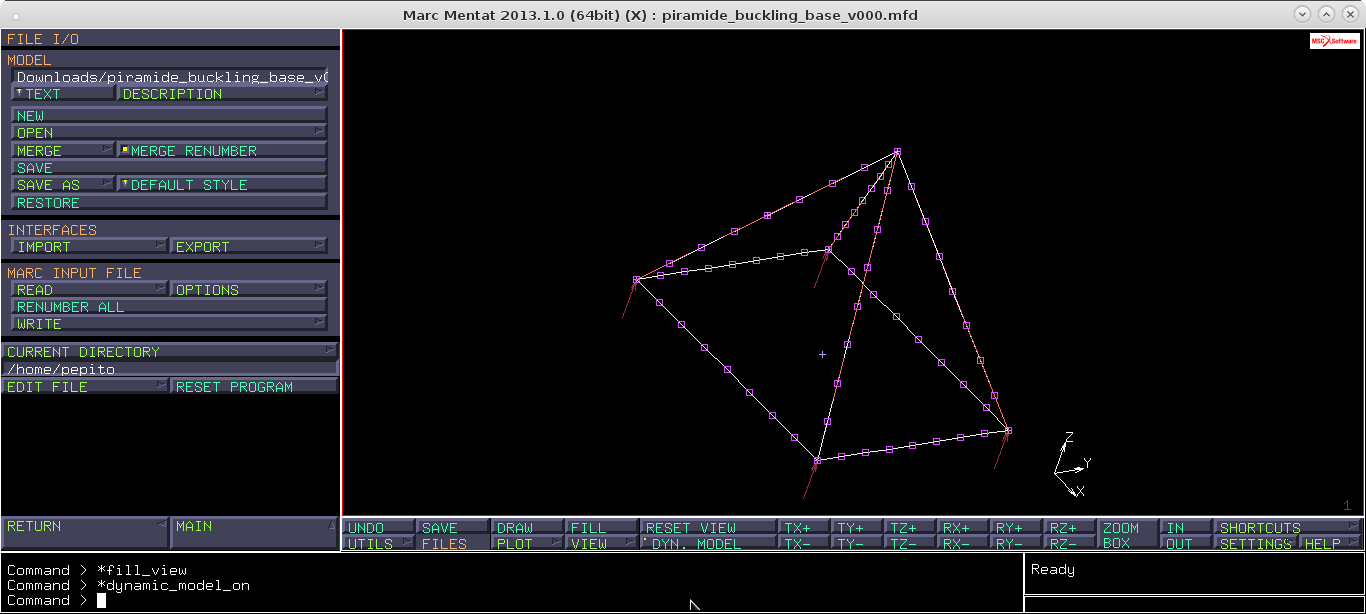
Apriamo il file del modello.
Esso contiene una struttura piramidale i cui dati sono i seguenti:
- base 600×750 mm
- altezza 600 mm
- sezioni tubolari con diametro esterno 12mm, spessore di parete 2 mm; quindi piuttosto snelle.
- alluminio 6060 T6, E=70000 MPA, ys~Rp02=165 MPa
La struttura è appoggiata sui quattro vertici della base, con posizionamento isostatico. Le giunzioni sono modellate per collasso nodale per assicurare continuità di rotazioni e spostamenti. E' applicato un carico verticale di 1000 N compressivo applicato al vertice superiore della struttura.
Il problema è già impostato manca solo la creazione del Loadcase.
Sono presenti quattro Boundary conditions: abbiamo il carico compressivo di 1000N in direzione z che definirà lo stato di carico 1. Le restanti sono gli appoggi in z sui quattro vertici e altri due vincoli per eliminare residui moti di corpo rigido.
Impostiamo l'analisi di instabilità creando il Loadcase.
Loadcase $\rightarrow $ new $\rightarrow $ buckle $\rightarrow $ name: predizione condizione critica soluzione lineare (Non tocco le proprietà che lascio di default) Questo servirà ad estrarre i fattori di scalatura $\lambda$ per determinare i carichi critici.
Creiamo il Job
Job $\rightarrow $ new $\rightarrow $ structural $\rightarrow $ name: buckling
Properties $\rightarrow $ initial loads $\rightarrow $ seleziono tutti i vincoli e lo stato di carico 1 (lo stato 0 non essendo definito sarà implicitamente quello scarico)
Job parameters $\rightarrow $ buckling modes: 10
Run $\rightarrow $ submit
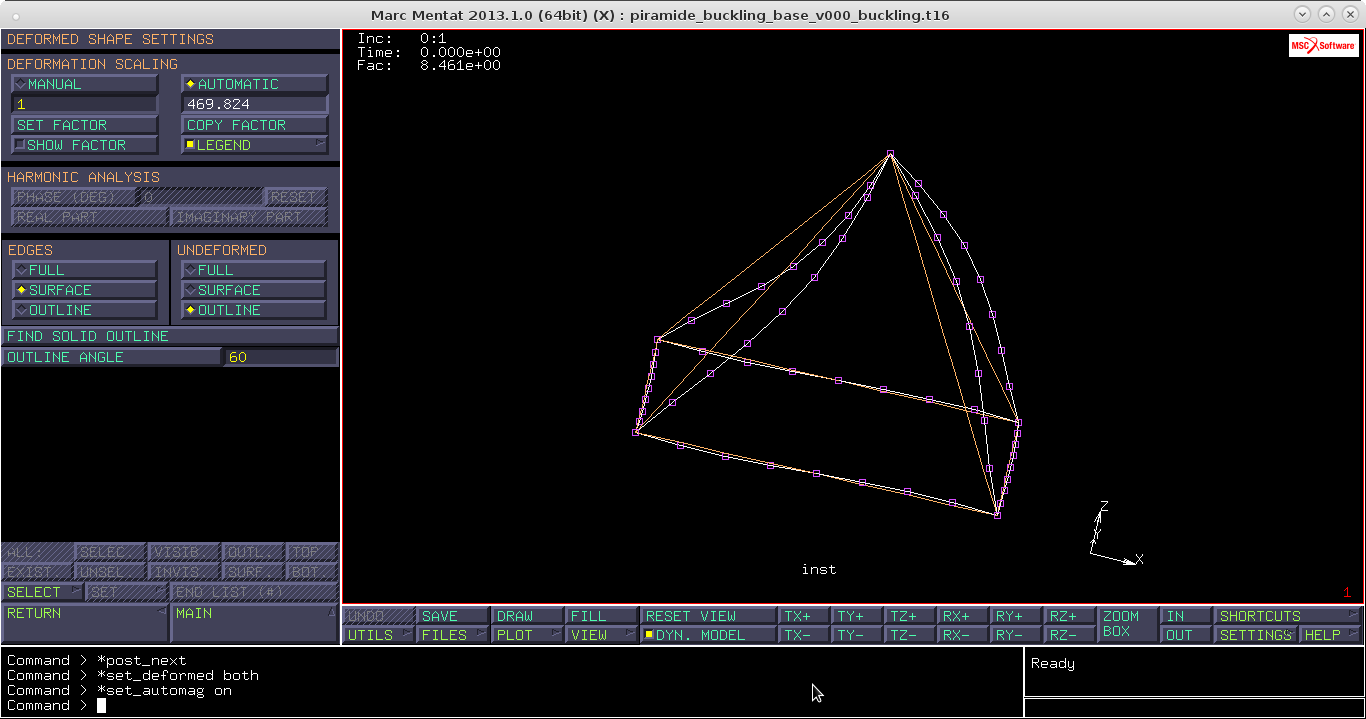
Apriamo il file dei risultati con Open post file
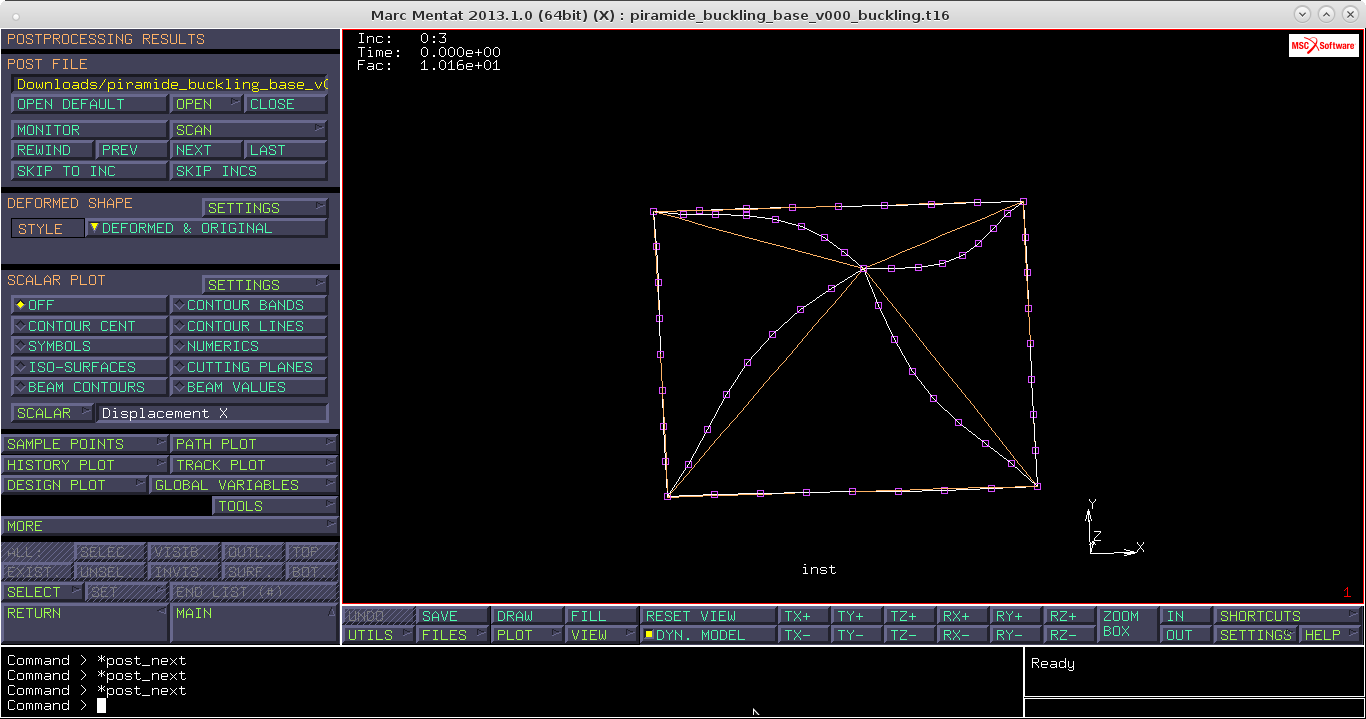
Notiamo che il primo fattore $\lambda$=8.46, quindi il primo carico critico è $P_{crit}$=8460N. Al secondo modo probabilmente non si arriva perchè significherebbe seguire la soluzione lineare oltre la criticità rilevata dal primo modo. Al terzo modo per $\lambda$=1.01 abbiamo la presenza di torsione.
Tabella di monitoraggio carico orario
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | |
|---|---|---|---|---|---|
| Giovanni Colangelo | 4 | — | — | — | — |
| Riccardo Bergamaschi | 4 | — | — | — | — |
| Ottaviani Giacomo | 4 | — | — | — | — |
| Arzilli Francesca | 4 | — | — | — | — |
| Revisore 1 | — | — | — | — | — |
| Revisore 2 | — | — | — | — | — |
| Revisore 3 | — | — | — | — | — |
| Revisore 4 | — | — | — | — | — |
| Totale | — | — | — | — | — |