−Indice
Carichi nodali Equivalenti/ effetto Vlasov su travi a torsione
Argomento della lezione
Nella prima parte della lezione è stato trattato il procedimento per passare da carichi distribuiti a carichi concentrati utilizzando il listato maxima preimpostato. Nella seconda parte è stato studiato l'effetto Vlasov su una trave sottoposta a torsione, mediante il software Marc.
Richiami teorici
Si considera un elemento parametrico a 4 nodi i,j,l,k estruso di un valore costante t come da figura
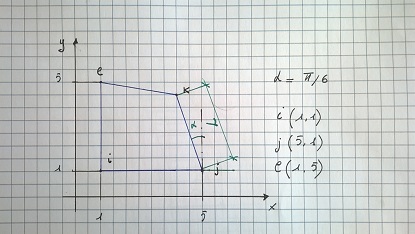
Viene applicato un carico di superficie di componenti Sx e Sy all'intera superficie laterale. Nel caso preso in esame, per il successivo listato maxima, si considera solo un carico nella sola direzione x, applicato al solo lato definito dai nodi j,k. Il carico è costituito da una componente costante di valore P, in direzione x, a cui si somma un carico a farfalla di intensità ΔP, in direzione x, come da figura.
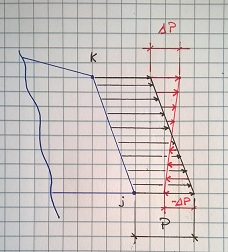
Ciò che si vuole ottenere, noto Sx, è il vettore delle forze nodali equivalenti Fscalcolabile con il seguente integrale di superficie
∫∫[Sx,Sy]Nds Considerando che lo spessore e' costante sul perimetro e che l'unico lato caricato e' quello jk l'integrale si trasforma cosi'
∫kj[Sx,Sy]Ntdl
Dove Sx e Sy sono i carichi, t e' lo spessore e N rappresenta una matrice [2×8] contentente termini legati alla funzione di forma alternati da 0.
Per lo svolgimento dell'integrale conviene operare un cambio di variabile passando nelle coordinate naturali [ξ,η] in quanto ξ=1 costante mentre −1<η<1.
Operando la trasformazione delle variabili, si ottiene una espressione per la la lunghezza infinitesima ∂l del tratto inclinato. Considerando che ξ=cost=1
∂l=√(∂x∂η)2+(∂y∂η)2
Sostituendo all`espressione del vettore delle forze nodali, si ottiene:
Fs=∫1−1[Sx,Sy]Nt√(∂x∂η)2+(∂y∂η)2∂η
E` possibile ricavare la forma esatta della primitiva di questo integrale. In linea teorica, se cio` non fosse possibile, sarebbe comunque approssimabile con la formula di quadratura di Gauss.
Per la parte in Maxima si riporta di seguito il link da cui scaricare il file del professore rielaborato con i commenti passo passo.
carichi_nodali_equivalenti_07.04.wxm.
Aree nodali d'influenza
Si mostra ora un procedimento per l'ottenimento dei carichi nodali concentrati più semplice rispetto al precedente ma difettoso.
Si consideri lo stesso elemento (ijkl) con gli stessi carichi applicati (P, dP). Le due componenti si possono studiare separatamente (sovrapposizione degli effetti) per cui per dP=0 i carichi concentrati nei nodi j e k valgono PtL2 dalla teoria energetica vista su maxima.
Si considera il lato jk diviso a metà, su ogni metà agisce dunque il carico P per la lunghezza L2 per lo spessore t. Il lato jk si dice allora diviso per aree di influenza nodali e la risultante applicabile all'unico nodo presente in quell'area è equivalente alla risultante calcolata con la conservazione energetica.
Si considera ora il contributo di dP con distribuzione a farfalla; ponendo nel risultato P=0 si ottiene che le risultanti su j e k sono −dPLt6 e dPLt6.
Cercando le risultanti nodali attraverso le aree d'ifluenza si divide a metà il lato jk in corrispondenza del punto in cui la distribuzione va a zero, così facendo ottengo due aree di influenza caratterizzate da carichi triangolari.
Se ne considera uno, la risultante sul nodo k si ottiene come dP∗L2∗t∗12 applicata a 23 del triangolo.
Si nota che il momento rispetto allo stesso polo o calcolato con i due metodi differenti cambia.
Mo(equiv.energ)=dPLt6Lcos(alpha);Mo(areeinfl)=23dPLt4Lcos(alpha);
La teoria delle aree d'influenza risulta comoda e dalla semplice implementazione, ma sovrastima di circa il 50% il momento risultante rispetto alla teoria del'equivalenza energetica in caso di carichi la cui distribuzione non è uniforme.
Studiando varie tipologie di mesh tuttavia si nota che l'errore commesso cala drasticamente con la taglia della mesh. A sostegno di ciò si osservi la figura in cui è schematizzata una diga caricata quindi da un carico a distribuzione triangolare. Si consideri in principio di avere una mesh a 4 nodi trapezoidale “molto grossa”. Su un elemento agisce quindi parte del carico scomponibile in una componente P costante e una dP triangolare di entità simile; il ragionamento dunque è analogo al caso precedente e l'errore risulta elevato.

Se ora si suppone di utilizzare una mesh ad esempio 8 volte più fitta si osserva che il carico triangolare dP applicato su un singolo elemento diventa praticamente trascurabile se confrontato con P e dunque anche l'errore commesso con il metodo delle aree d'influenza rispetto all'equivalenza energetica risulta minimo.

Effetto Vlasov su trave a torsione
Aprire il programma Mentat e caricare i file profilo_aperto_analisi_vlasov_2d.mud di inizio lezione e profilo_analisi_vlasov_estruso_gruppob.mud di fine lezione.
Viene considerata una sezione di trave aperta a C, definita nel piano, inizialmente di spessore nullo. Viene modellata meta`sezione, invece di un solo quarto poiche` si assume che il piano XZ sia di antisimmetria. La sezione da sottoporre a momento torcente sul piano XZ deve essere chiusa, quindi l`oggetto iniziale va duplicato per simmetria. Vengono duplicate le sole curve, poiche` essendo entita` geometriche, non aumentano le incognite del problema, cosa che invece avverrebbe se fossero duplicati i nodi.
Si definisce il piano di simmetria zx passante per il nodo corrispondente all'origine e normale ad y
MESH GENERATION—>SYMMETRY—>(impostare valori 0,0,0 in POINT e 0,1,0 in NORMAL), selezionare “CURVES” quindi
“ALL: EXIST”
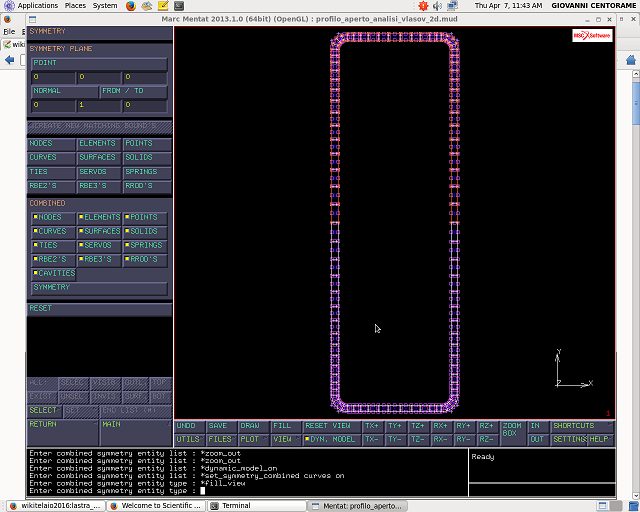
Il piano di simmetria e` simmetrico sia per la sezione che per la trave e il caricamento a momento torcente e` 3 volte antisimmetrico rispetto al piano. Inizialmente gli elementi della sezione sono elementi quadrilateri a 8 nodi, quindi le funzioni di forma agli spostamenti sono quadratiche. E` possibile rappresentare le deformazioni paraboliche dei lati inizialmente rettilinei. L`analisi a torsione viene condotta attraverso un raffronto tra una modellazione a elementi isoparametrici a 4 nodi, e una a 8 nodi, per stabilire la presenza di eventuali errori dovuti alla meshatura.Confrontando i risultati, si puo` stabilire se la modellazione a 4 nodi e` sufficientemente approssimata e quindi significativa.
Si procede ad effettuare il cambio di classe degli elementi da quadratici a lineare
MESH GENERATION—>CHANGE CLASS—>TO LINEAR ELEMENTS—>(selezionare i nodi della sezione in cui operare il cambio di classe)—> ALL: SELEC.—> END LIST

Poiche` la sollecitazione avviene fuori piano, non si puo` limitare l`analisi al solo elemento piano, quindi la sezione va estrusa. Si sceglie di estrudere dagli elementi isoparametrici a 4 nodi una sola “fila” , ottenendo cosi` dei parallelepipedi a 8 nodi. Anche in questo caso non si e` sicuri della meshatura, quindi bisognera` effettuare una comparazione dei risultati ottenuti con diverse estrusioni.
Il codice per effettuare l`estrusione di una singola fila e` il seguente:
MESH GENERATION—>EXPAND—>TRANSLATIONS—> ( l`estrusione avviene lungo Z per 2 mm, quindi si inseriscono le coordinate (0,0,2)—> REPETITIONS (1, rappresenta il numero di file da estrudere)—>MODE—>REMOVE( rimuove gli elementi di partenza dopo l`estrusione)—>ALL:EXIST—>END LIST

alternativamente a REMOVE, si puo` scegliere SHIFT per spostare gli elementi di partenza a fine estrusione, oppure SAVE per lasciare gli elementi di partenza nella loro posizione, senza spostarli o rimuoverli.
Dopo questa operazione, alcuni nodi potrebbero essere stati duplicati e sovrapposti. Si rende necessario farli collassare in un unico nodo attraverso il comando SWEEP.
MESH GENERATION—>SWEEP—> ( tutti i nodi entro una tolleranza impostata a piacere verranno collassati in un unico nodo) ALL: EXIST
Si impongono le proprieta` geometriche:
GEOMETRIC PROPERTIES—>NEW—>STRUCTURAL—>3D—>SOLID—> NAME( MASSELLO)—>ELEMENTS—>ADD—>EXIST.
Selezionando la voce PROPERTIES nello stesso menu` si trova la voce ASSUMED STRAIN. Il significato di tale comando verra` illustrato nella lezione successiva. In generale se il comando e` spento, il programma non e`in grado di modellare il comportamento di questa struttura, ad esempio nel caso di una pressione interna applicata o nel caso di due momenti flettenti applicati ai due bracci della sezione a forma di ipotetico diapason. Questo si risolve o mettendo piu` elementi sullo spessore, anche piu` di 4, invece del singolo elemento attuale, oppure utilizzando elementi quadratici. Se il comando viene attivato, anche gli elementi lineari vengono utilizzati per cogliere in maniera esatta la risposta ad un momento flettente costante applicato alla parete.
Viene persa tuttavia la continuita` degli spostamenti tra elemento ed elemento della parete.
Poiche` la struttura e` caricata a torsione che non genera flessione delle pareti, ASSUMED STRAIN puo` essere spento.
Si associa il materiale:
MATERIAL PROPERTIES—>NEW—>STANDARD—>NAME(ALLUMINIO)—>TYPE—>STANDARD—>ELEMENTS—>ADD—> ALL: EXIST

Quindi le Boundary Conditions, definendo i vincoli di antisimmetria, applicando momenti torcenti e rimuovendo eventuali moti di corpo rigido. Si inseriscono per primi i vincoli di antisimmetria negli omonimi piani ZX con normale Y e XY con normale Z. Si esamina la struttura valutando quali gradi di liberta` devono essere bloccati sui nodi che giacciono sui piani di antisimmetria per garantire la continuità degli spostamenti. Si imposta il primo vincolo di antisimmetria sul piano XY normale a Z.
BOUNDARY CONDITIONS—>NEW—>STRUCTURAL—>FIXED DISPLACEMENT—> NAME( antisym:nz_pxy)
Devono essere nulli gli spostamenti lungo X e Y e la rotazione attorno a Z PROPERTIES—> spuntare DISPLACEMENT X,Y ROTATION Z
Questa condizione va applicata a tutti i nodi che giacciono sul piano di antisimmetria.
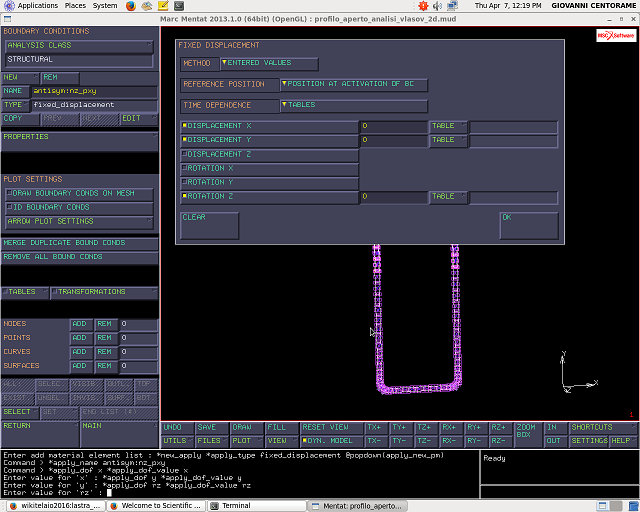
La seconda B.C. riguarda il piano ZX normale a Y.
BOUNDARY CONDITIONS—>NEW—>STRUCTURAL—>FIXED DISPLACEMENT—> NAME( antisym:ny_pzx)
Questa condizione non viene applicata a tutti i nodi del piano di antisimmetria poiche` la sezione in realta` non e` chiusa ma presenta un taglio in corrispondenza di uno dei lati. Se si garantisce la continuita` del materiale la sezione e` chiusa e non e` presente il taglio. Se non viene vincolata la continuita` del materiale, si ottiene una sezione aperta. Si passa da sezione aperta a sezione chiusa, semplicemente accendendo o spegnendo un vincolo.
Devono essere nulli gli spostamenti lungo X e Z e la rotazione attorno a Y PROPERTIES—> spuntare DISPLACEMENT X,Z ROTATION Y
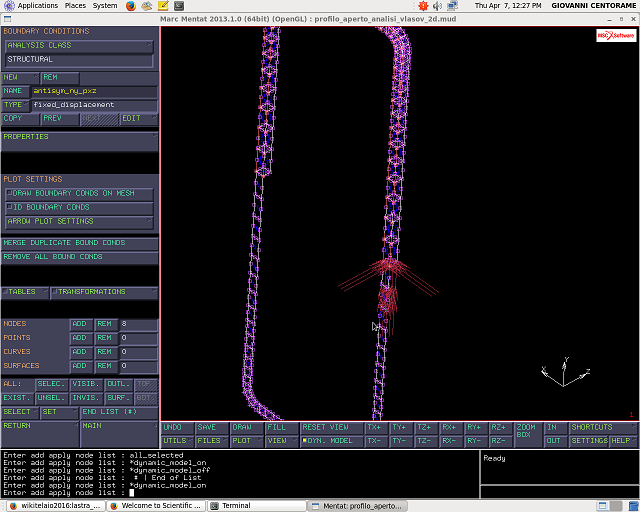
Questa condizione si applica ai nodi giacenti sul piano di antisimmetria ZX per i quali deve essere garantita la continuita` del materiale del corpo modellato e la sua immagine.
Si va a creare una variante della precedente B.C. sui nodi della sezione tagliata. Se e` attiva, la sezione e` chiusa, altrimenti aperta.
BOUNDARY CONDITIONS—>NEW—>STRUCTURAL—>FIXED DISPLACEMENT—> NAME(variantechiusa:ny_pzx)
Devono essere nulli gli spostamenti lungo X e Z e la rotazione attorno a Y PROPERTIES—> spuntare DISPLACEMENT X,Z ROTATION Y
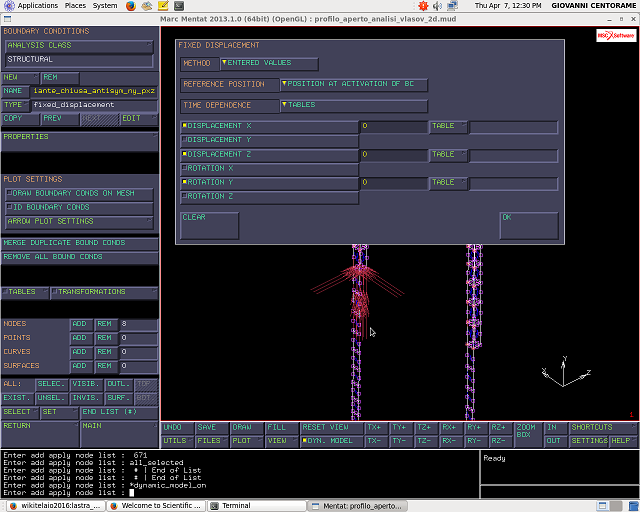
Va applicata ai soli nodi che si trovano sul taglio. Se questa B.C. e` attivata la sezione e` saldata, altrimenti no.
Ora va applicato il momento torcente. IL problema e`che i nodi del modello non supportano rotazioni, e in tal caso neanche momenti, perche` i momenti svolgerebbero lavoro su rotazioni inesistenti. Se una trave e` soggetta a puro momento torcente, i nodi della sezione soggetta a torsione presentano uno spostamento fuori piano,quindi si ha spostamento Z libero tra i nodi, ma gli spostamenti XY entropiano sono indipendenti nodo per nodo, devono seguire una legge di moto di corpo rigido. Si considera una proprieta` valida nel caso di sezione elastica che prevede che presi due nodi sulla stessa sezione, la loro distanza sul piano di sezione non varia dopo aver applicato il momento torcente.
In pratica si puo` costruire un corpo rigido sulla sezione qui considerata, imponendo che i nodi nel piano XY debbano seguire il corpo rigido nel suo moto in tutti i gradi di liberta` tranne nello spostamento Z. Cosi` facendo si crea un legame tra il corpo rigido creato e i nodi della sezione. Il vantaggio e` che su un corpo rigido si puo` applicare momento torcente e dunque il problema viene aggirato.
Si va a costruire il corpo rigido sulla sezione del concio di trave. Il corpo rigido presenta 6 gradi di liberta` nello spazio, 3 rotazioni e 3 traslazioni, e sono supportati da un nodo, che rappresenta una “maniglia” ossia un nodo di controllo del corpo rigido. Si costruisce un nodo specifico nel baricentro della sezione(COORDINATE 20,0,2),2 rappresenta lo spessore del modello, per guidare il corpo rigido nel suo moto.
MESH GENERATION—>NODES—>ADD—> (COORDINATE…)
Il concetto di corpo rigido rappresenta un vincolo cinematico tra i nodi della struttura, il quale fornisce rigidezza infinita e deformazione elastica nulla. I vincoli cinematici si trovano sotto il menu LINKS. Il corpo rigido utile per questo studio e` chiamato rbe2_1 ( rigid body elemet 2_1).
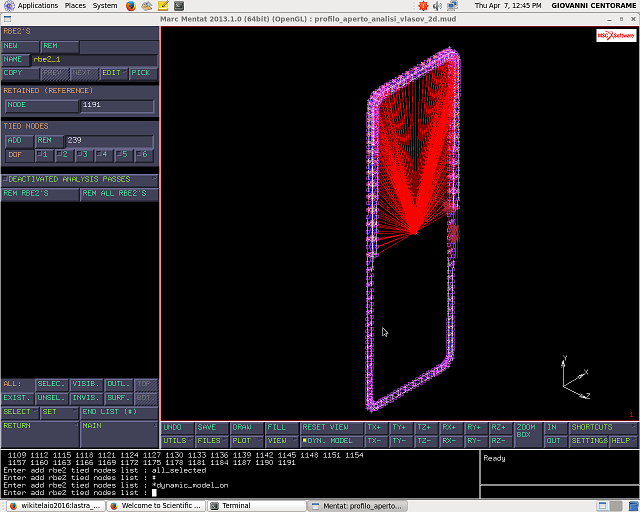
LINKS—>RBE2_1—> RETAINED ( rappresenta il nodo di riferimento del corpo rigido, in questo caso quello appena creato, da selezionare)—> TIED ( rappresenta i nodi il cui moto e` dipendente da quello di riferimento; le caselle indicano i gradi di liberta` che i nodi devono seguire: 1-3 traslazioni, 4-6 rotazioni, osservare l`immagine )
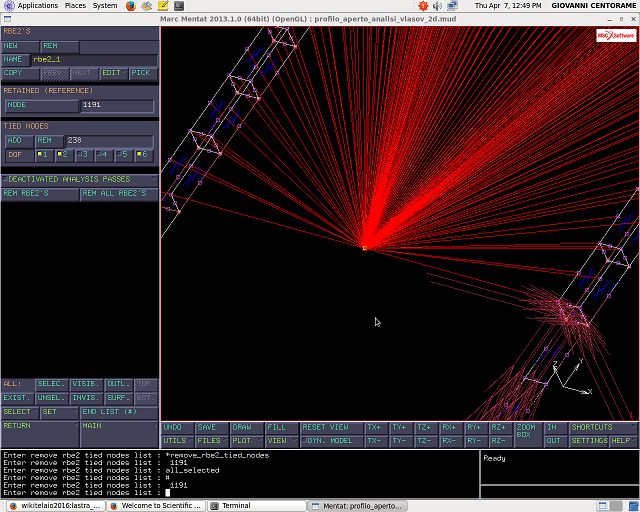
Dall`immagine si nota quali sono i gradi di liberta` che i nodi devono soddisfare: spostamenti X,Y bloccati, liberta` in direzione Z. Per le rotazioni, vengono considerate indipendenti solo quelle con assi entro piano, quindi la 4 e 5 ( in direzione X e Y).
Nel caso in cui il nodo centrale fosse inserito casualmente anche tra i nodi TIED, il solutore presenta, una volta avviato il calcolo il codice 2011(errore) invece di 3004 percio' il nodo deve essere rimosso.
Il nodo centrale di ancoraggio e` sul piano di antisimmetria e si deve applicare un vincolo di antisimmetria perche` il corpo rigido ha una sua immagine dall`altra parte del piano antisimmetrico. Se non si applica il vincolo, nel caso di un corpo rigido che interseca il piano di antisimmetria, il corpo stesso e la sua immagine si possono muovere in maniera indipendente l`uno dall`altra.
Si applica quindi la B.C. al nodo di ancoraggio:
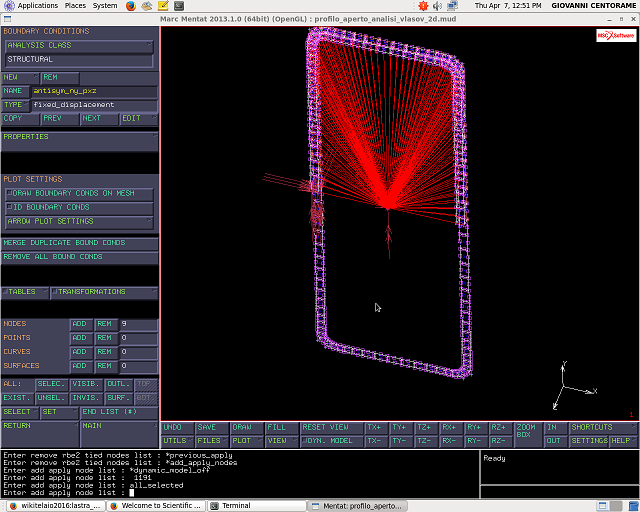
Non si applica la B.C. di antisimmetria al piano XY poiche` il punto di controllo non passa a cavallo del piano XY stesso.
Si creano delle B.C. al corpo rigido che ne definiscano univocamente la sua posizione, da applicare al nodo di controllo.

N.B. Le proprieta` di questo vincolo sono: spostamento Z definito nullo in quanto non derivabile dalla sua connessione con la struttura. Lo stesso concetto e` valido per le rotazioni in X e Y, in quanto si generano spostamenti relativi tra corpo rigido e struttura in Z che sono ammessi.
Ultima B.C. della lezione da imporre e` il momento torcente.
BOUNDARY CONDITIONS—>NEW—>STRUCTURAL—>NAME(momento torcente unitario)—>POINT LOAD—>MOMENT Z (1 Nmm)
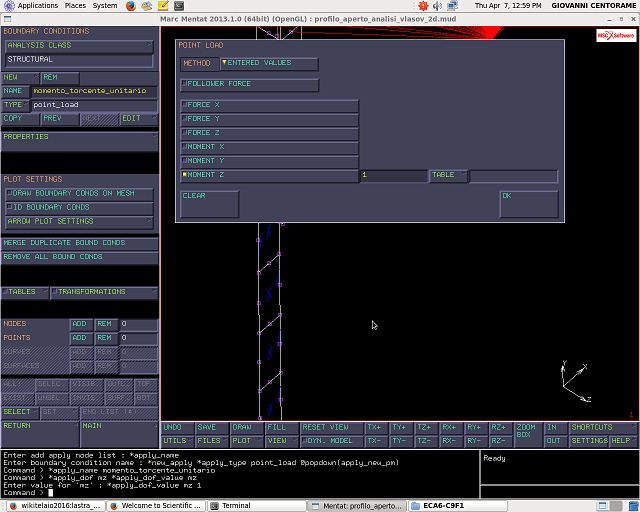
In pratica si applica un momento di nota entita` e si osservano le rotazioni associate. Si commette tuttavia un errore.
In nodo di controllo a cui viene applicata la B.C e` sul piano di antisimmetria, quindi anche la corrispondente immagine del punto e` posizionata sullo stesso piano. Se si carica il punto, si applica la condizione due volte, poiche` viene caricata anche la sua immagine. In quel punto dello spazio viene applicato un momento di 2 Nmm, ovvero di entita` doppia. Per avere applicato un momento unitario,e` necessario imporre MOMENT Z (0,5 Nmm).

Lista dei simboli
| x,y | direzioni del piano cartesiano |
| P,dP | carico sull'elemento con distribuzioni costante e variabile linearmente |
| i,j,k,l | nodi dell'elemento |
| L | lunghezza del lato jk |
| t | spessore di cui si suppone estruso l'elemento ijkl |
| Sx,Sy | carichi di superficie nelle direzioni x e y |
Riferimenti
Appunti e registrazione della lezione del 7/04/2016
Autori, note e ringraziamenti
Autori
Stefano Caprioli, mat. 104799, Giovanni Centorame, mat. 104299, Andrea Menini, mat. 103586.
Tabella di monitoraggio carico orario
Ore-uomo richieste per la compilazione della pagina.
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Caprioli | 12 | — | — | — | — |
| Centorame | 12 | — | — | — | — |
| Menini | 12 | — | — | — | — |
| Riccardo Bergamaschi | 1 | 2 | — | 0.5 | — |
| Revisore 2 | — | 1 | — | 1 | — |
| Revisore 3 | — | 2.5 | — | 1.5 | — |
| Revisore 4 | — | — | — | — | — |
| Totale | 36 | 5.5 | 3.5 | 3 | — |
La sezione relativa ai revisori è da compilarsi a cura del curatore. </hidden>
Note di revisione
PATTUME
Spostare qui il materiale caricato dal docente non utilizzato a lezione