Indice
Effetto Vlasov su Trave caricata a torsione
File di partenza:profilo_aperto_analisi_vlasov_3d_v002.mud
Note sul vincolamento: per impedire il moto di corpo rigido di rotazione attorno a X era stato bloccato lo spostamento in Z di uno dei nodi della faccia esterna della struttura. In alternativa si può impedire la traslazione lungo Y del nodo di controllo (Y è la direzione tangenziale nel moto di rotazione attorno a X, se la impedisco impedisco il moto)
Assi locali
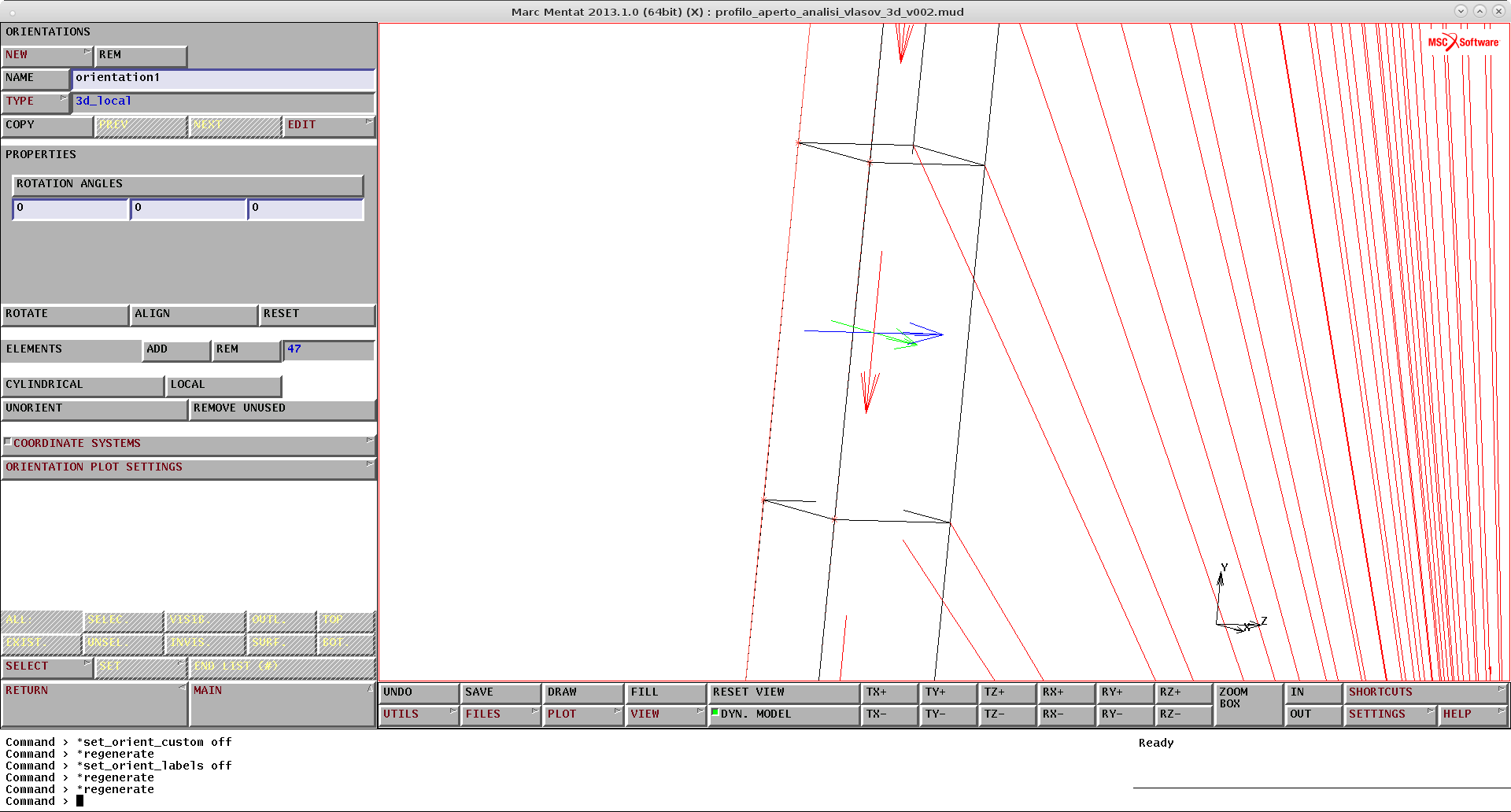
Avendo creato la mesh per estrusione è possibile definire per ogni elemento un sistema di riferimento locale, utile per visualizzare meglio le tensioni dato che non tutti gli elementi sono orientati nello stesso modo rispetto al sistema di riferimento globale. Vengono definiti 3 assi di 3 diversi colori orientati in funzione degli assi locali dell’elemento che sono legati alla posizione dei nodi. -Rosso: I asse, 1° nodo → 2° nodo -Verde, II asse, 2° nodo → 3° nodo -Blu, 3° asse, 1° nodo → 2° nodo Nel caso in esame il materiale è isotropo, precisamente alluminio, ma nel caso di un materiale composito, ad esempio, gli assi definiscono le direzioni delle fibre Per visualizzare, modificare o rimuovere l’orientazione locale si procede come segue:
Material Properties----> Orientation----> New----> 3-D Local
Concio di trave
Calcolo sezione aperta
Prima di lanciare il calcolo siscegliere di includere nei risultati i valori di tensione riferiti ai sistemi locali:
Job----> Properties----> Jobs Results----> Stress in preferred system
Si esegue poi il calcolo
Job----> Run ----> Submit
Analisi Risultati
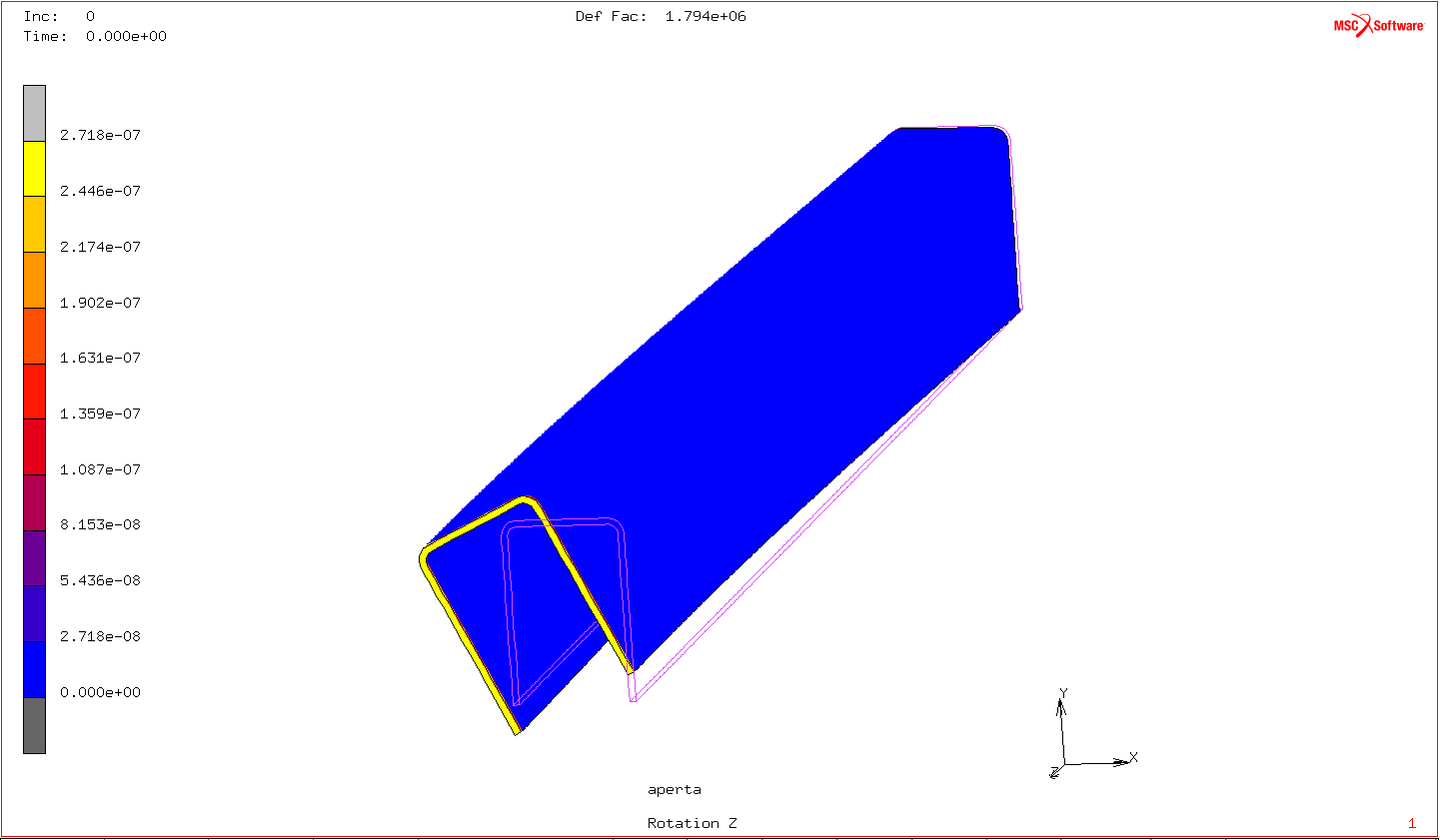
Osservando la deformata è possibile notare l’effetto di Warping, ovvero una notevole distorsione ( che ne caso in esame è visibile come un vistoso spostamento ) dei nodi di una sezione planare. Per poter apprezzare la deformazione è utile impostare un fattore di amplificazione della deformazione di 10^5.
Equivalent stress
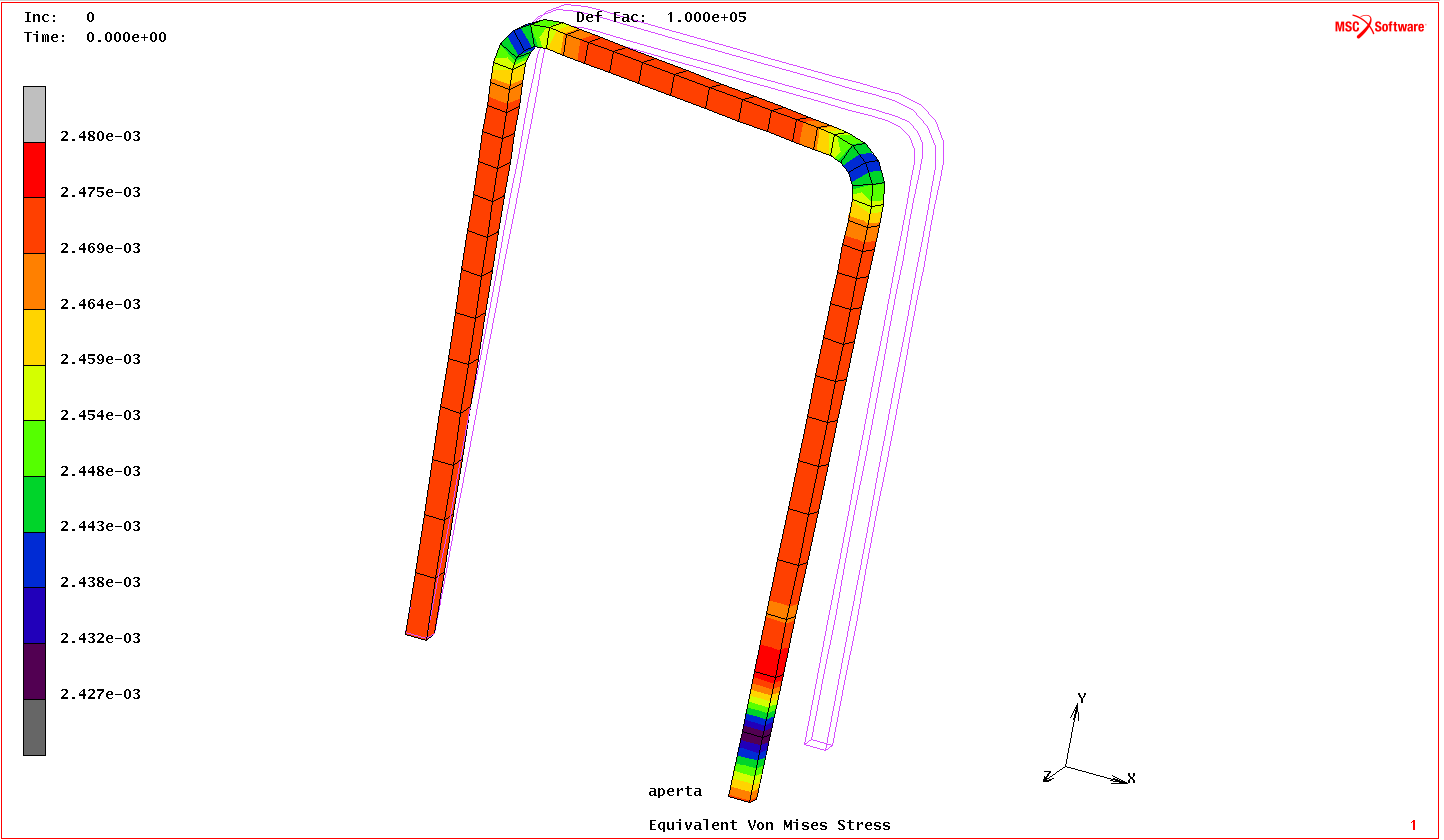
Nell’analisi delle tensioni andiamo a flaggare “Equivalent Von Mises Stress” e “Equivalent of stress” che, nel caso in cui il calcolo sia lineare, coincidono. Possiamo dire che mentre la prima è la von mises vista dal solutore, la seconda è quella vista dal programma, calcolata a posteriori dalle 6 componenti di tensione. E’ importante notare come la Von Mises sia uniforme sulla parete interna; in realtà è continuamente variabile ma il programma interpola fra i due valori massimi che si trovano agli estremi dell’elemento e visualizza una soluzione in cui la tensione è costante e il minimo non viene visualizzato
Component 23 of stress
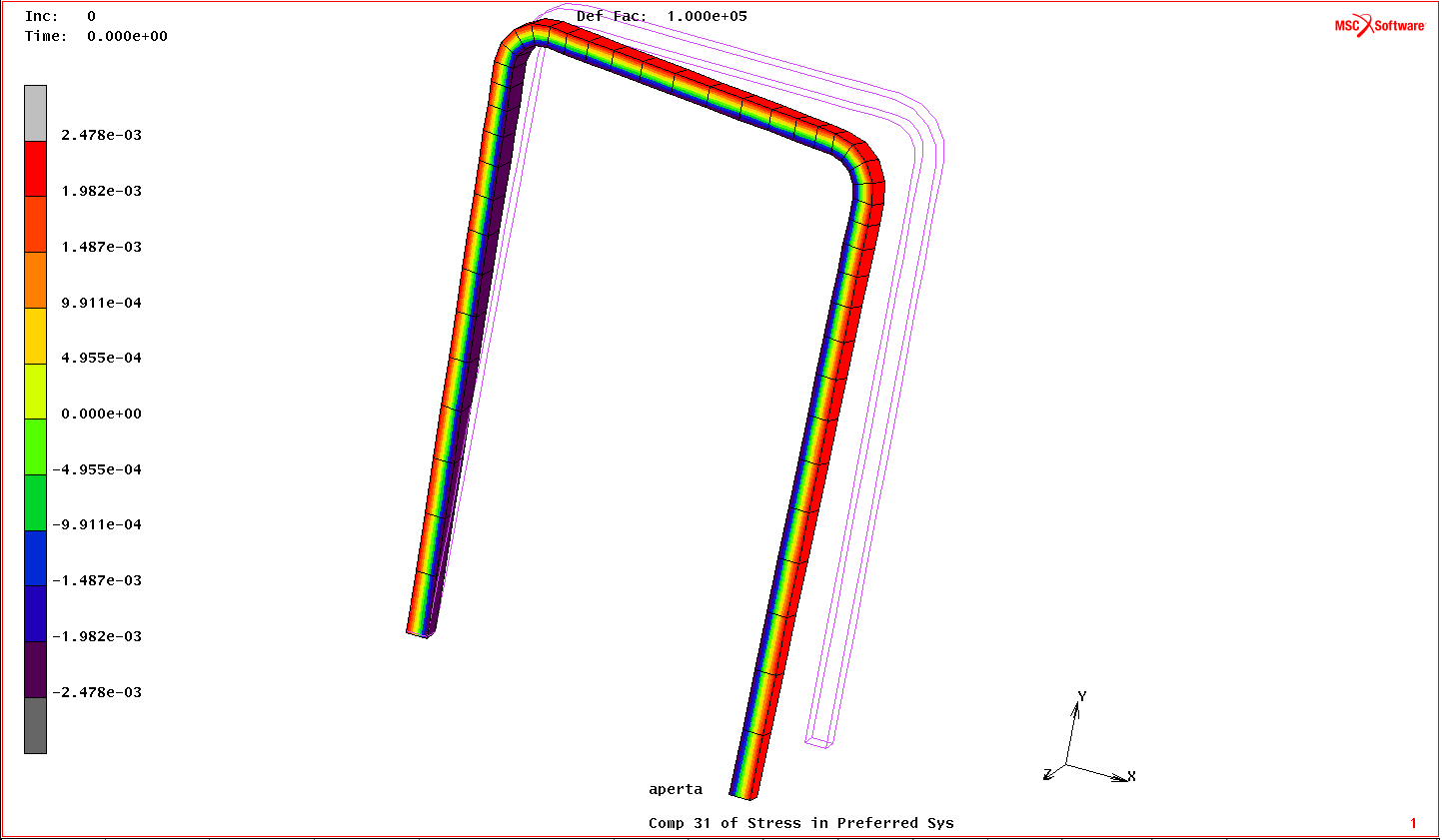
La component 23 of stress ( riferita al sistema globale ), ovvero la τyz non è costante sul profilo ( passa da negativa a positiva ). Ricordiamo che gli assi globali sono così definiti: -x: normale alla parete del profilo; -y: intraprofilo; -z: normale alla sezione. Tale componente induce una deformazione a parallelepipedo opposta fra la faccia inetrna ed esterna del profilo, passsa infatti da un valore positivo a uno negativo. Per visualizzare la stessa componente sul tratto orizzontale di struttura si attiva la component 31 of stress Per la visualizzazione su tutti gli elementi attivare la component 31 of stressi in preferred system.
Component 23 of stress in preferred system
le 2 sezioni alla base della struttura visualizzata avranno comportamento diverso, ma ho una mesh troppo grezza per poterlo notare bene;
Con una mesh più raffinata si ottiene:
Le tensioni appaiono continue solo perché nella visualizzazione viene imposta la continuità. Per visualizzare l’andamento reale basta disattivare il “nodal averaging”:
Scalar Plot -> Settings -> Extrapolation -> Nodal Averaging -> OFF
Fatto ciò si può vedere la discontinuità delle tensioni, soprattutto nei tratti curvi della sezione.
E’ possibile vedere l’andamento irregolare delle τ plottandone l’andamento lungo y su un grafico:
Pathplot -> Nodepath
Si selezionano alcuni nodi sulla superficie esterna partendo dall’estremo tagliato
Add Curves -> add curve
Scegliere “arc Lenght” per l’asse X e “component 23 in preferred system” per l’asse Y.
Andiamo ora a calcolare la rigidezza torsionale tramite foglio di calcolo excel: L’obiettivo è confrontare i valori del modulo di rigidezza nel caso in cui la struttura sia aperto e chiusa. NB: la rotazione relativa ha valore doppio rispetto a quello misurato sulla sezione inquanto è presente un’antisimmetria
Foglio di calcolo completo:foglio_di_calcolo_rigidezza_torsionale_trave.ods
Calcolo sezione chiusa
Per eseguire il calcolo a sezione chiusa impostiamo in Initial Loads la variante chiusa e lanciamo il submit. Notiamo che si ha svergolamento (warping) ed omogeneità lungo l’asse z ma in misura molto minore rispetto al caso precedente, in particolare di 4 ordini di grandezza. Un’altra differenza che si nota è che la component 31 of stress rimane circa costante su tutto lo spessore. La differenza fra i valori di rigidezza delle due sezioni è notevole. Nota: le sezioni aperte sono infinitamente meno rigide rispetto a quelle chiuse per quanto riguarda un calcolo a torsione, mentre il calcolo a flessione evidenzia un comportamento sostanzialmente identico.
Validazione modello di calcolo
E’ possibile validare il modello di calcolo utilizzato eseguendo lo stesso su una sezione più lunga e duplicando il modello rispetto al piano di antisimmetria. Si ottiene continuità degli spostamenti senza averla imposta e ciò indica la correttezza del calcolo.
Trave finita
E’ utile ora indagare sul caso in cui la trave non sia infinitamente lunga per scoprire se si verifica ugualmente la perdita vistosa di rigidezza. Si va perciò a creare una trave di lunghezza 1200mm, 10 volte la dimensione caratteristica attuale ( 120mm ). Lo si fa accedendo al menu Mesh Generation → Move e impostando lo “Scale factors” a 1 1 300
Mesh Generation -> Move -> Model
Si procede poi alla suddivisone tramite il comando subdivide impostando la sezione division a 2 2 300 e applicando la divisione a tutti gli elementi. Il numero dei gradi di libertà è così aumentato di un fattore 300. Andiamo perciò a collassare i nodi generati tramite
Mesh generation----> Sweep---->Nodes----> exhist
ATTENZIONE: nel passaggio da singola fetta riscata alle 300 fette ottenute per suddivisione della stessa genero nuovi nodi sul piano di antisimmetria xz. A questi nuovi nodi deve essere applicato il vincolo di antisimmetria!!!.
Se lanciassi ora il calcolo una fetta sarebbe rappresentativa dell’intera trave e perciò resterebbe tutto invariato; risulta differente invece se ai terminali fosse impedito lo svergolamento ( ad esempio fossimo nel caso il cui vi fosse una saldatura con una piastra più grande e maggiormente rigida ). Ciò si realizza imponendo che le sezioni alle estremità rimanga piane: -1° estremo sarà infinitamente rigido e senza svergolamento -2° estremo sarà libero e con svergolamento Dal menù selezioniamo gli RBE2 e si attivano tuttii numeri da 1 a 6 ( moto di corpo rigido ).
Links -> Rbe’s 2
In questo caso, analizzando i risultati, è possibile vedere come la teoria del Saint-Venant sottostimi di 52 volte il valore finale, non esaltando il notevole irrigidimento della struttura.
Files della lezione
File base: profilo_aperto_analisi_vlasov_3d_v002.mud Mesh raffinata:modello_profilo_aperto_stvenant_analisi_tau_sezione_apertura.mud Trave finita: profilo_analisi_incastriterminali_v003.mud Foglio di calcolo: foglio_di_calcolo_rigidezza_torsionale_trave.ods
Autori, note e ringraziamenti
Autori
Paris Mauro, mat.103991
Santucci Marco, mat. 218936
Punzo Stefano, mat 219578
Dignatici Marco, mat 91642
Tabella di monitoraggio carico orario
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Dignatici Marco | 3 | — | — | — | —- |
| Paris Mauro | 4 | — | — | — | – |
| Punzo Stefano | — | — | — | — | — |
| Santucci Marco | 8 | — | — | — | - |
| Davide Segatori | 1.5 | — | — | — | – |
| Giacomo Davoli | 1 | — | — | - | - |
| Luigi Amico | 1 | — | — | — | - |
| Revisore 4 | — | — | — | — | — |
| Totale | - | —- | —- | - | — |
</hidden>
Pattume
Modello postazioni inizio lezione profilo_aperto_analisi_vlasov_3d_v002.mud
Modello cattedra inizio lezione profilo_aperto_analisi_vlasov_3d_v002_cattedra.mud
ATTENZIONE: nel passaggio da singola fetta riscata alle 300 fette ottenute per suddivisione della stessa genero nuovi nodi sul piano di antisimmetria xz. A questi nuovi nodi deve essere applicato il vincolo di antisimmetria!!!.
Modello a lunghezza finita, terminali incastrati a fine lezione (corretto come sopra) profilo_analisi_incastriterminali_v003.mud
Foglio di calcolo per rigidezze torsionali foglio_di_calcolo_rigidezza_torsionale_trave.ods
Andamento tensioni tangenziali nell'intorno del taglio sul profilo aperto modello_profilo_aperto_stvenant_analisi_tau_sezione_apertura.mud