Indice
modello postazioni inizio lezione
Riga di comando per lanciare Mentat
mentat2013.1 -ogl -glflush
EFFETTO VLASOV 3D
La lezione mira a concludere l'analisi al Marc, iniziata la lezione precedente, sul profilato soggetto a momento torcente unitario. Si affronteranno i seguenti punti:
- Analisi della nuova boundary condition “posizionamento_blocco_rx”
- Soluzione senza il nuovo vincolo
- Analisi dei gradi di libertà bloccati dalle Boundary Conditions
- Soluzione corretta con il nuovo vincolo
- Analisi della deformata con bc corrette
- Analisi delle tensioni
- Calcolo delle rigidezze torsionali per sezione aperta e chiusa
NUOVA BOUNDARY CONDITION
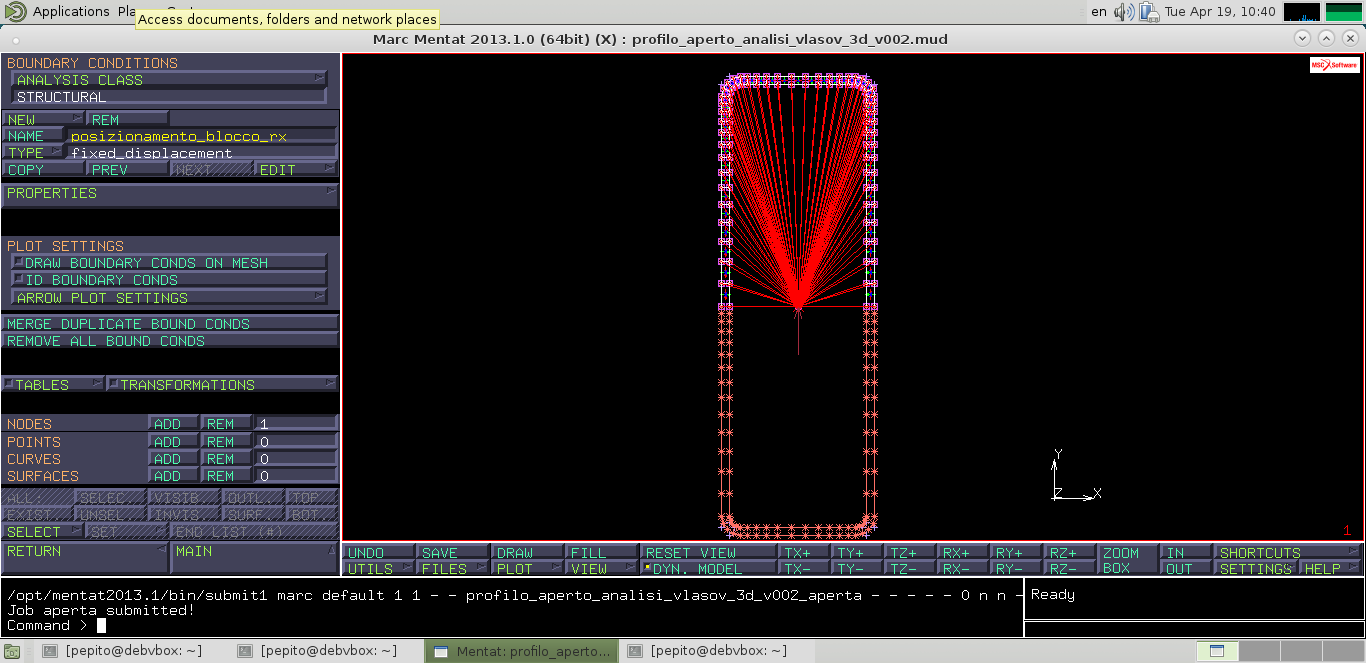
Il corpo rigido creato risulta solo parzialmente vincolato alla sezione creata; infatti rimane labile rispetto a rotazioni attorno all'asse x che si possono tuttavia bloccare con l'attivazione della boundary condition (BC) “posizionamento_blocco_rx”.
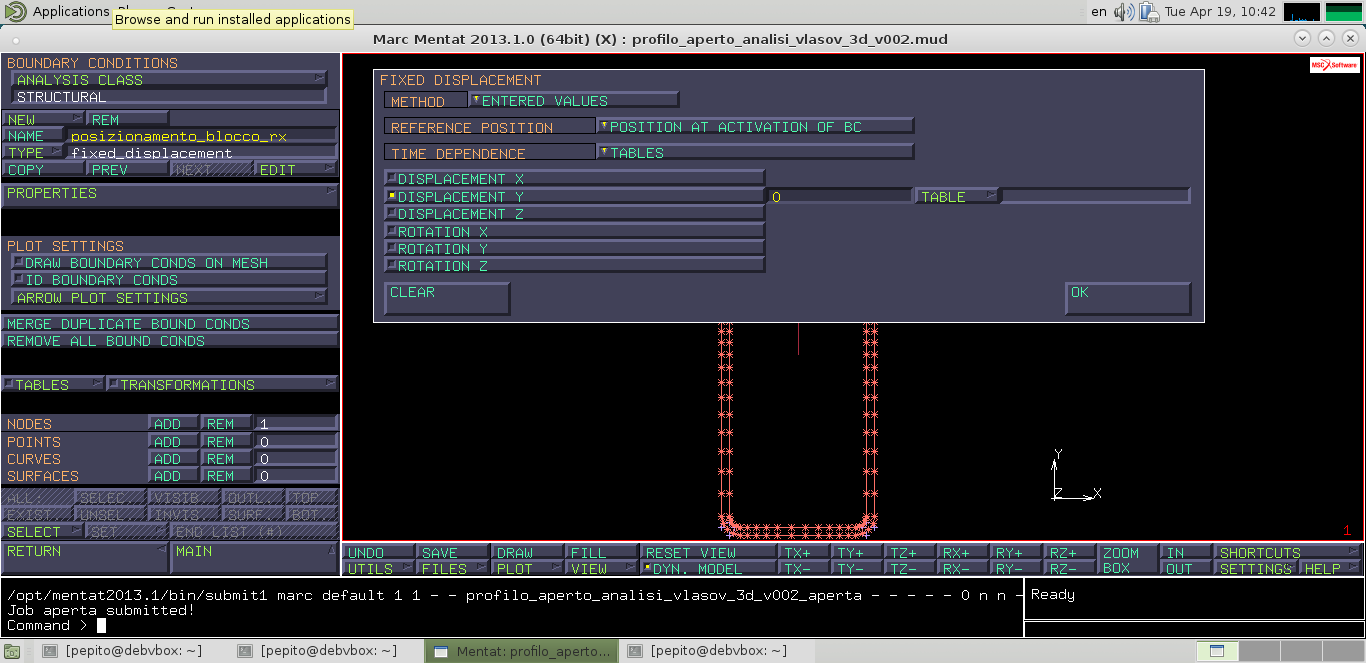
Iter procedurale per attivazione BC: main –> boundary conditions –> new –> structural –> fixed displacement –> Name: Posizionamento_blocco_rx –> properties: disp y = 0 –> selezionare il nodo centrale
SOLUZIONE SENZA IL NUOVO VINCOLO
Nel seguito si effettuerà l'analisi dei risultati FEM senza aver attivato la BC discussa in precedenza. Iter procedurale per lanciare il calcolo: Job –> properties –> disattivo BC variante chiusa e BC posizionamento blocco rx –> ok –> Run —> Submit . Si ottiene:
Si osserva che il termine singularity ratio (SR) è pari a 9.7e-17 (molto piccolo, praticamente zero); ciò denuncia singolarità per la matrice di rigidezza (a rigore, per la sua inversa). Non viene tuttavia visto come errore dal calcolatore, che restituisce un exit number di 3004 (per essere errore, dovrebbe essere 2004). Comunque, il fatto di imbattersi in un SR così piccolo sostanzialmente denuncia la presenza di una labilità residua nel sistema in esame, che sarà quindi necessario individuare ed eliminare con opportune BC (in particolare, quella discussa al paragrafo precedente).
ANALISI DEI GRADI DI LIBERTA' BLOCCATI DALLE BOUNDARY CONDITIONS
Da una rapida analisi del sistema, si osserva che per realizzare il vincolamento della struttura rispetto a rotazioni attorno all'asse x è sufficiente bloccare le traslazioni lungo y (nel piano della sezione in esame, di normale z)
I nodi giacenti sul piano xy, tuttavia, sono già vincolati a seguire i moti del nodo centrale: è necessario quindi applicare la nuova BC al solo nodo centrale, essendo l'unico ad avere spostamento y indipendente.
SOLUZIONE DEL MARC CORRETTA CON IL NUOVO VINCOLO
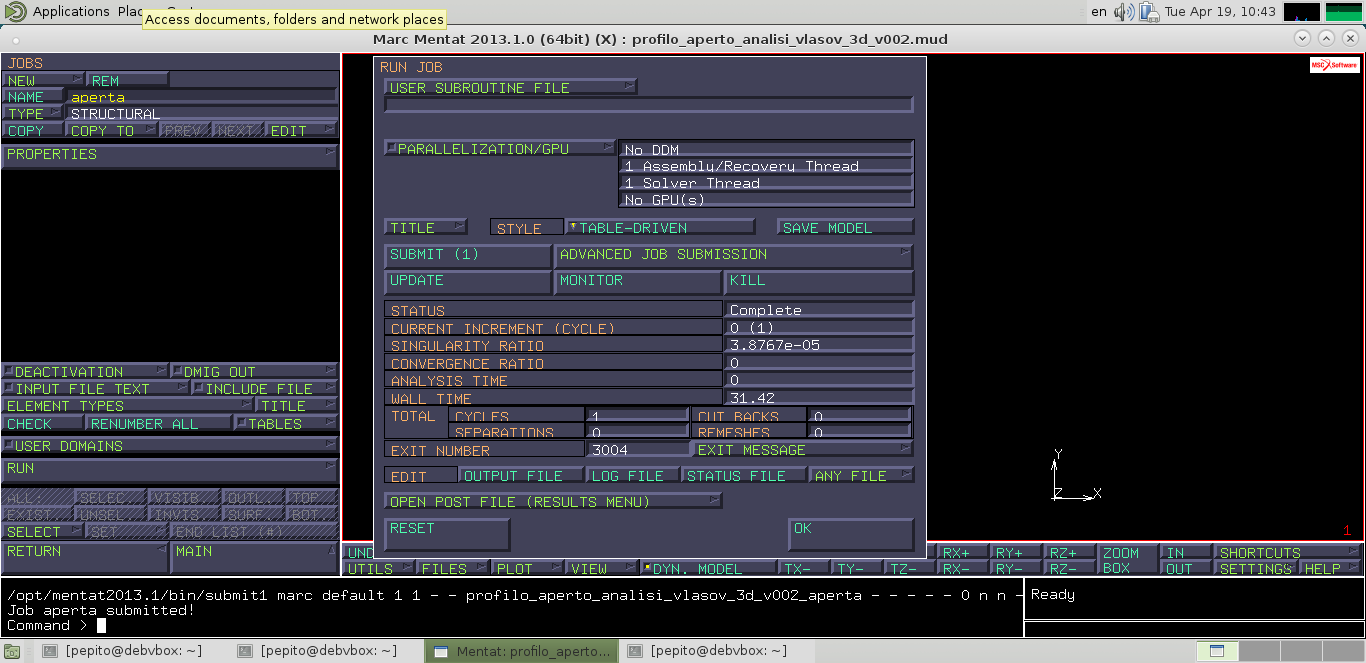
Lancio della simulazione considerando la BC precedentemente discussa: Main –> Job –> properties –> initial loads (verificare che rimanga esclusa solo BC variante aperta) –> run –> submit. Si osserva:
Ora si è ottenuto un SR dell'ordine di e-5, che corrisponde ad avere una matrice di rigidezza ben condizionata (il range di accettabilità è [e-6,e-9]).
ANALISI DELLA DEFORMATA CON BC CORRETTA
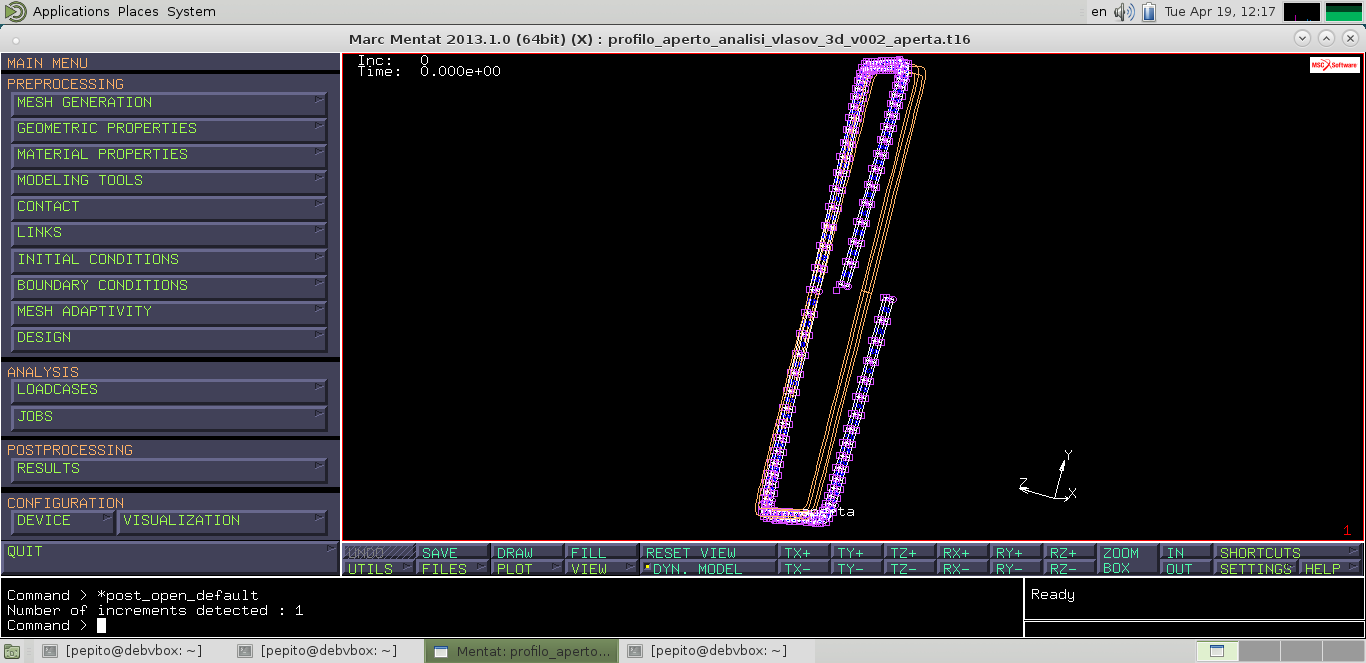
Prima di fare l'analisi è necessario duplicare il modello seguendo la procedura: main –> mesh generation –> simmetry –> point (0,0,0) e normal (0,1,0) –> simmetry –> all existing. Lanciare quindi il calcolo e aprire il file dei risultati (.t16) da “open post file results”. Dal menu in cui ci si trova selezionare “deformed e original” per analizzare la deformata del concio di trave rispetto alla posizione nello spazio assunta in condizioni indeformate.
Di seguito viene invece riportata l'immagine della deformata per il caso di sezione sottile chiusa, sottoposta allo stesso carico. E' necessario in questo caso aggiungere un'ulteriore boundary condition: jobs –> properties –> initial loads –> variante sezione chiusa.
ANALISI DELLE TENSIONI
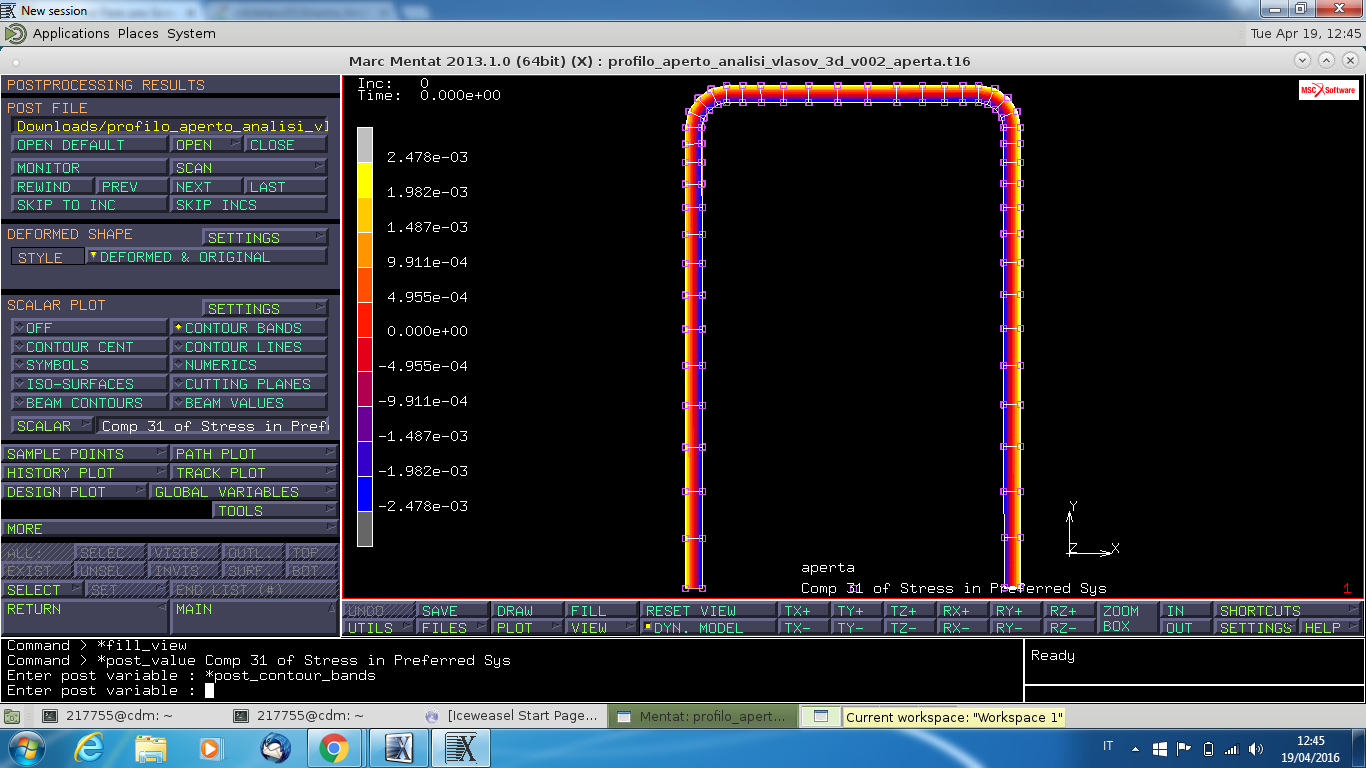
Volendo analizzare l'andamento della tensione equivalente secondo la formulazione del Von Mises seguire la procedura: post processing –> scalar –> equivalent of stress in preferred system –> contour bands.
La tensione di Von Mises appare costante lungo lo spessore della sezione in figura, risultato che non è coerente con la teoria della scienza delle costruzioni secondo cui l'andamento delle tensioni taglianti (tau) per le sezioni sottili aperte sottoposte a momento torcente ha un andamento a farfalla (lineare). Questo difetto è intrinsecamente connesso alla formulazione della tensione equivalente precedentemente utilizzata: per sua stessa definizione essa comporta la perdita dei segni delle tensioni effettive. Di conseguenza il calcolatore si troverà nelle condizioni di dover interpolare con legge lineare due valori estremali uguali in modulo ed in segno, situazione che comporta la visualizzazione di una tensione costante (errata) lungo lo spessore (nota: a causa di questo fatto non viene erroneamente visualizzato l'annullamento delle tau lungo la linea media della sezione sottile in esame).
Analizzando invece le tensioni tau (componente 31) nel sistema locale (base elemento) di riferimento si può notare che l'andamento risulta coerente con quello teorico (farfalla).
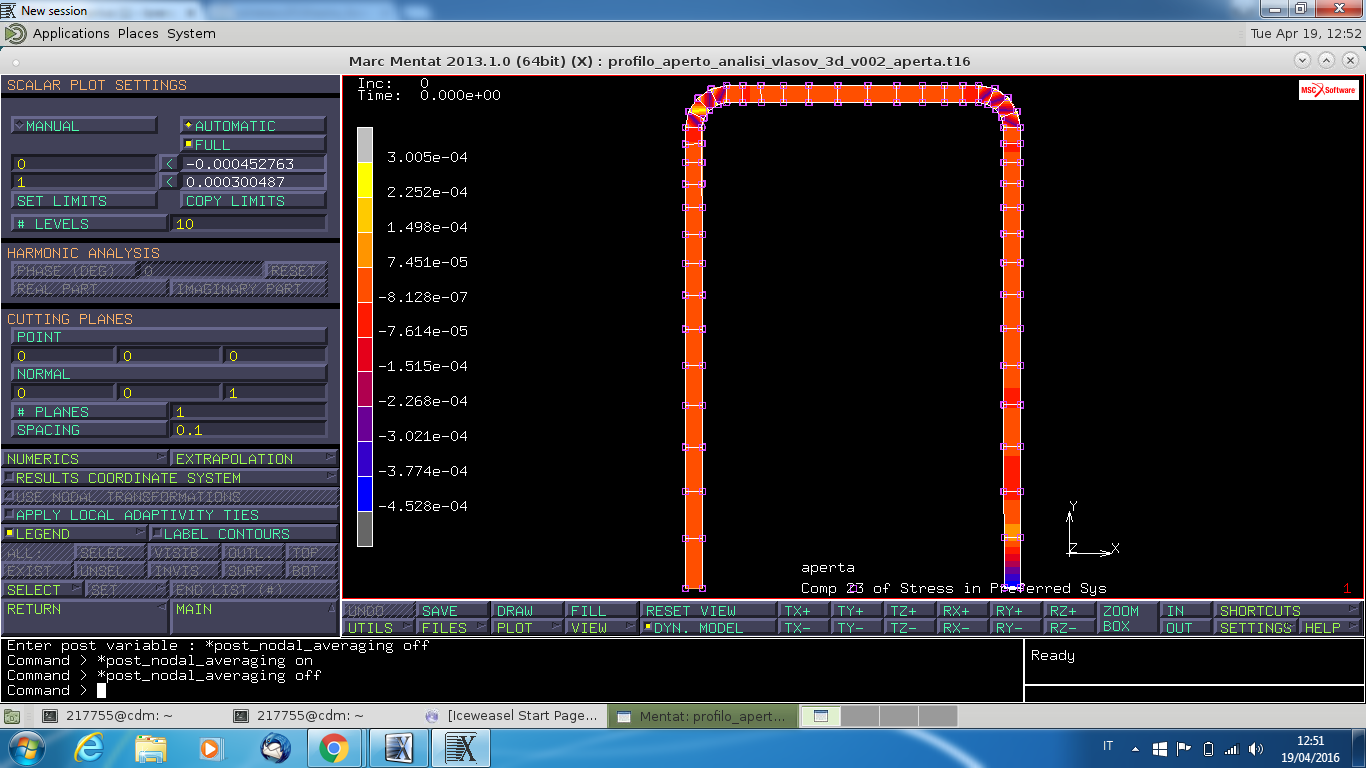
Considerando invece le tensioni tau 23, è noto da teoria che devono essere non nulle solo nell'intorno della sezione tagliata. Dal risultato al Marc invece si nota che queste componenti di tensione sono in contrasto con la teoria:
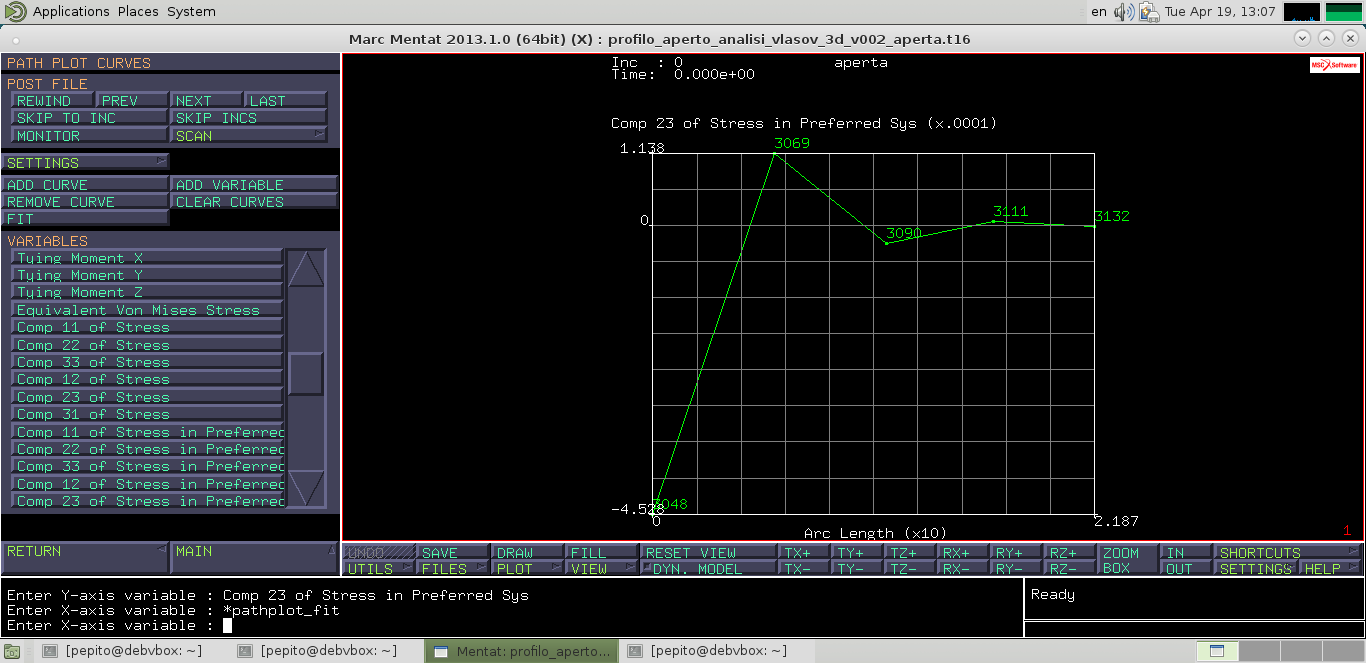
Iter per plot andamento delle tau23 : pathplot –> nodepath –> seleziono 5 nodi sulla superficie esterna destra del concio di trave –> add curves –> add curve –> asse x = arclenght , asse y = comp. 23 in preferred sys. –> fit
L'andamento teorico dovrebbe essere del tipo esponenziale decrescente, dalla figura precedente (plot risultati FEM nell'intorno del taglio) si osserva invece un andamento discontinuo.
CALCOLO DELLE RIGIDEZZE TORSIONALI PER SEZIONE APERTA E CHIUSA
Di seguito l'impostazione di un foglio di calcolo automatico per valutare e confrontare le rigidezze torsionali nei due casi considerati utilizzando valori teorici e quelli ottenuti dal calcolo FEM. Dai conti è evidente la differenza di rigidezza torsionale tra sezione sottile aperta e chiusa: quest'ultima, dati i maggiori valori assunti dal termine Kt (a parità di carico, dimensioni e materiale) risulta più resistente (e quindi adatta) a carichi torsionali.
IMPOSTAZIONE GEOMETRIA PER LEZIONE SUCCESSIVA
1) mesh generation –> move –> scale factors [1 : 1 : 300] (estrusione concio di trave per 600mm - considerare anche l'immagine, quindi 1200mm di estrusione totali -)
2) mesh generation –> subdivide –> divisions [1 : 1 : 300] (realizzazione di 300 elementi lungo l'asse di estrusione) –> sweep all
3) ricordarsi che sarà necessario (nella prossima lezione) applicare opportuni vincoli di antisimmetria alla struttura creata
Autori:
- Gianluca Bafaro 97512
- Antonio Montagnani
- Francesco Ambrogi
- Lorenzo ERMANNO Degli Esposti
Tabella di monitoraggio carico orario
Ore-uomo richieste per la compilazione della pagina.
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Antonio Montagnani | — | — | — | 5 | |
| Francesco Ambrogi | — | — | — | 5 | |
| Lorenzo Degli Esposti | — | — | — | 5 | |
| Gianluca Bafaro | — | — | — | 5 | |
| Manuel Baraldi | 1 | — | — | — | — |
| Francesco Maria Drago | 1 | — | — | — | — |
| Revisore 3 | — | — | — | — | — |
| Revisore 4 | — | — | — | — | — |
| Totale | — | — | — | — | — |
La sezione relativa ai revisori è da compilarsi a cura del curatore. </hidden>