Indice
Effetto Vlasov su travi a torsione
RBE - Rigid Body Element
I RBE sono strumenti potentissimi e molto utilizzati a FEM e sono sostanzialmente delle equazioni che si aggiungono al problema $ F= k * \delta $. Ce ne sono di due tipi, RBE2 e RBE3.
RBE2
Si condensa in un unico punto un blocco di materiale indeformabile avente i suoi propri moti rigidi. Anch’esso è quindi vincolabile e può essere collegato ad una struttura attraverso l’utilizzo dei “dof”: questi sono i tipi di collegamenti (displacemente x-y-z, rotation x-y-z) infinitamente rigidi tra il RBE2 e la struttura (n.b. il RBE non vincola la struttura, quindi se questa è labile rimane labile, inoltre lui stesso può portare labilità). Il collegamento avviene tra il “reference” (RBE2) e i nodi “tied” posti su corpo da collegare. Pongono dei vincoli sugli spostamenti relativi.
Ci sono diversi esempi di utilizzo del RBE2:
- un motore portante collegato ad un telaio da moto; non lo modello ma lo inserisco come RBE2 e lo collego rigidamente al telaio;
- nel caso di sospensioni rigide (anche se di solito vengono usati i beam);
- per elementi di rigidezza di ordine di grandezza superiore a quella delle altri componenti del sistema.
Superelemento
Il RBE2 è diverso dal superelemento (utilizzato molto spesso in aeronautica). Un esempio di superelemento possono essere le ali di un aereo: alla giunzione con la fusoliera (nodi di interfaccia del modello) si immaginano poste come delle molle, la cui rigidezza è imposta sotto forma di matrice dipendentemente dalle proprietà dell’ala. Il RBE2 invece, come già affermato, è infinitamente rigido. I superelementi sono strumenti molto utilizzati, poiché nel caso statico danno risultati sicuri al 100%; ma se passo ad uno studio dinamico l’accoppiamento diventa complicato poiché si abbandona l'ambito lineare.
RBE3
Il Rigid Body Element 3 ha la stessa definizione formale del RBE2, però i suoi vincoli non sono sugli spostamenti relativi, bensì sulle forze e le coppie. In pratica, caricando con una forza il nodo reference, il RBE3 non applica semplicemente la stessa forza uguale e contraria a tutti i nodi tied (come invece avveniva con gli spostamenti per il RBE2), ma la distribuisce tenendo conto della distanza del nodo al reference e facendo un equilibrio locale su tutti i punti considerati.
Nel modello...
Nel modello, abbiamo applicato un momento torcente al reference (RBE2), lo abbiamo vincolato e abbiamo applicato i dof 1,2 e 6 (ovvero abbiamo bloccato i moti relativi displacement x e y e rotation z). In particolare tutto questo è stato chiamato “moto imposto”: il moto del corpo rigido, nelle altre direzioni che non ho dato ai dof, è stato imposto essere nullo. Avendo un RBE2, applicando un momento torcente nel baricentro, questo viene spalmato su tutti i tied ma la sezione rimane rigida; viceversa, se avessi utilizzato un RBE3 avrei avuto lo stesso effetto sui nodi, ma la sezione non sarebbe rimasta rigida (le distanze relative, prima imposte costanti, ora non lo sono più).
Modello
Lo scopo del modello è quello di osservare il diverso comportamento di sezioni aperte e chiuse, in particolare la differente reazione a torsione e flessione. Quella che è stata applicata alla sezione è una torsione a effetto Vlasov: a causa della rotazione per torsione si generano momenti flettenti sulla sezione considerato, fatto che non avviene nella teoria classica. Questo effetto è particolarmente importante nei brancardi delle autovetture, nella fattispecie nelle zone di saldatura.
Spiegazione
Tornando al modello, questa è una fettina di trave che può essere aperta o chiusa a seconda dei vincoli imposti (si sfrutta per questo la simmetria della struttura). Gli elementi che sono stati utilizzati per la mesh sono gli “Hex (8)”, ovvero brick lineari isoparametrici, paralleli dei “Quad (4)” in 3D. Come materiale è stato utilizzato lo standard, ponendo come modulo di elasticità e coefficiente di Poisson quelli dell’alluminio (70000 MPa, 0.3). Inoltre è stata attivata l’impostazione “orientations – 3d_local”, quindi si è posta anche la proprietà geometrica “mech_three_solid”, ovvero di massiccio.
Le Boundary condition imposte sono:
- l’antisimmetria nel piano xz di normale y (fixed_displacement);
- la sua variante per la sezione chiusa;
- l’antisimmetria nel piano xy di normale z (fixed_displacement); questo simula la continuità degli elementi finiti, dato che noi vediamo solo l’ultima fettina della trave;
- il moto imposto al RBE2 (ovvero il vincolo al RBE2) (fixed_displacement);
- il momento torcente imposo al “reference” (point_load); (n.b. poiché si sta applicando il momento soltanto a metà della sezione totale il momento segnato dal programma deve essere la metà di quello desiderato);
- il posizionamento del blocco (fixed_displacement);
Per la spiegazione dei vincoli di antisimmetria si rimanda alle lezioni precendenti.
Infine, sono stati creati due diversi “jobs”, uno per la sezione aperta e uno per la sezione chiusa, che verranno lanciati separatamente analizzando i risultati.
Risultati
Si può osservare che la struttura chiusa sostanzialmente rimane piana ma quando vengono amplificati gli spostamenti della torsione bisogna stare attenti, poichè, quando si ha una torsione pura siamo in presenza di spostamenti tangenziali; se questi si amplificano, lo fanno anche le componenti x e y (radiali) e questo porta ad un aumento di raggio, il che è fisicamente inaccettabile.
Aprendo il file della struttura aperta invece, si osserva come l'andamento degli sforzi tangenziali sulla sezione ha un comportamento molto diverso: infatti dove la sezione è aperta si nota uno svergolamento, ovvero la struttura ha un comportamento asimmetrico.
Visualizzando la componente 33 di sigma e la componente 11, che fanno riferimento a dei momenti flettenti, dove la struttura è aperta non si creano momenti flettenti, dato che abbiamo una sezione libera. Se si imponesse che la struttura debba rimanere piana, si formerebbero invece dei momenti flettenti secondari che creerebbero una distorsione.
Esempio trave a T
Se metto in torsione una trave a T, cioè le applico momento torcente, ho una zona che si ingobba ma che non è soggetta a momento flettente, mentre nella sezione incastrata si viene a creare un momento flettente secondario massimo. La struttura in quest'ultima zona vorrebbe ingobbarsi, ma, poichè non lo può fare, essendo vincolata, genera questo momento flettente secondario massimo; Questa è una zona molto critica qualora essa sia ottenuta per incollaggio, dal momento che si possono creare dei fenomeni di peeling (cioè una zona in cui la colla è soggetta a trazione) che possono determinare una rottura.
Rigidezza
Per quanto riguarda la rigidezza invece si guardano spostamenti, rotazioni, forze e coppie: Nel nostro caso, dato che ci interessa la rigidezza torsionale delle sezioni, si osserva la rotazione di esse dovuta alla coppia imposta, in modo da mettere in relazione la differenza di rigidezza tra le sezioni.
Per sapere la rigidezza relativa bisogna visualizzare la rotazione relativa tra le sezioni e per farlo occorre visualizzare le rotation z (numerics) corrispondente al RBE nei nodi linkati, sia nella struttura aperta che in quella chiusa. Il rapporto tra i due vale 648, per cui la rigidezza della trave chiusa è 648 volte più grande di quella a sezione aperta; quindi, per esempio,i brancardi è preferibile progettarli a sezione chiusa qual'ora sia possibile.
Trave mista
Come esempio di applicazione degli RBE2 realizzeremo una trave in meshatura mista lunga 300 mm, incastrata in una estremità e caricata dall’altra. Essi verranno utilizzati per dare continuità di sforzi tra i diversi tipi di mesh. Per fare ciò ci sono diverse vie, ad esempio creare due diversi RBE2 sui punti medi estremali (reference) e legarli sui nodi estremali della mesh (tieds), per poi legare i due RBE2. Un altro modo (quello che useremo in seguito) è legare le due estremità di due mesh adiacenti ad un unico reference. La trave che utilizzeremo è lunga 300 mm, a sezione circolare cava con raggio medio di 10 mm e spessore 4 mm. Essa è divisa in questo modo:
- 0 – 100 mm è utilizzato il metodo mesh 3D;
- 100 – 200 mm è utilizzato il metodo shell;
- 200 – 300 mm è utilizzato il metodo beam.
Passaggi e osservazioni
Cominciamo col posizionare quattro punti per definire le tre sezioni.
mesh generation → point add → (0,0,0) , (100,0,0) , (200,0,0) , (300,0,0)
3D
Partiremo con la mesh 3D. Ci posizioneremo nel piano YZ , noto il raggio esterno (12 mm) e il raggio interno (8 mm), posizioneremo a queste distanze due nodi lungo Y relativamente al punto (0,0,0). Creeremo una line tra i due, la si suddividerà in quattro parti ed eseguirò due expand. La prima expand sarà di 5 gradi per 72 volte; la seconda sarà lungo x (di translation) di 10,0,0 per 10 volte.
premere RY+ fino ad allinearsi ai punti (porsi nel piano YZ)
nodes add → 0,8,0 (raggio interno)nodes add → 0,12,0 (raggio esterno)element class → line (2) elements add → unire i due nodisubdivide → division → 4,1,1 (è il vettore locale dell'elemento u,v,w) → elements → selezionare la line → tasto destro
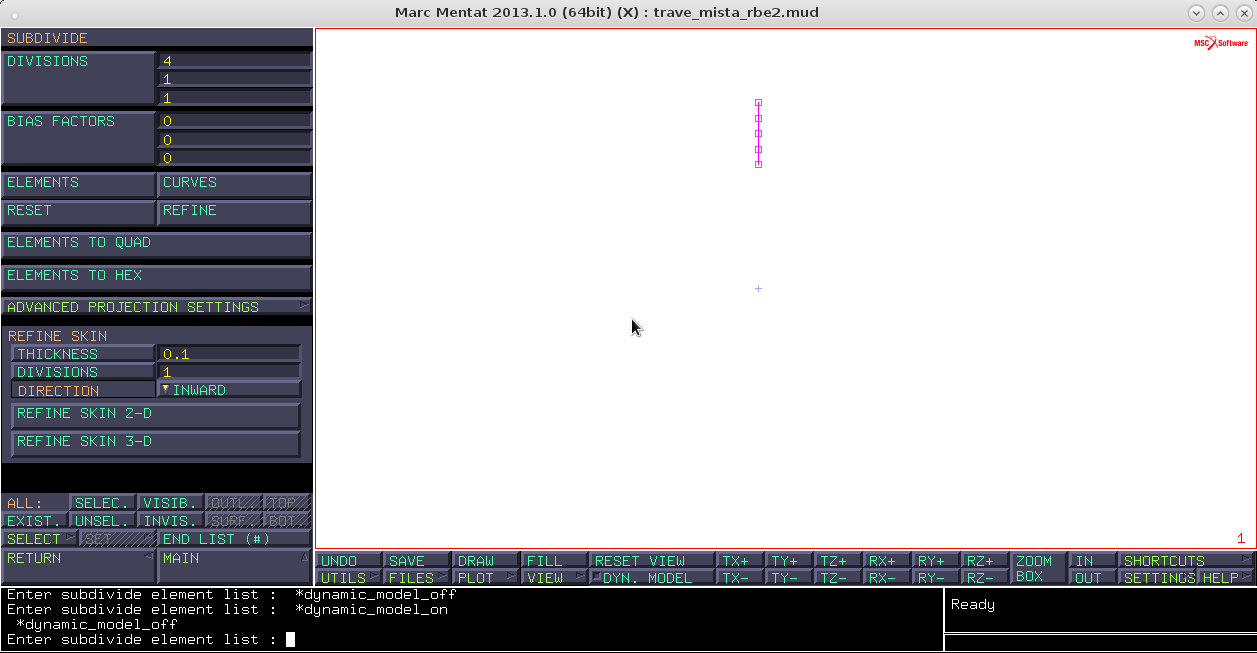
Vediamo il comando expand: questo comando serve per passare da un ordine di dimensione al superiore (line → shell, shell → 3D). Le specifiche del comando sono:
- rotation angles (è l'angolo per ogni ripetizione);
- repetitions (è il numero delle ripetizioni);
- centroid (è il centro su cui avviene l'expand);
- remove (rimuove l'entità di partenza);
- shift (l’entità di partenza viene spostata alla posizione finale);
- save (l’entità di partenza rimane salvata alla posizione iniziale);
expand → rotation angles 5,0,0 → repetition 72 → mode remove → elements → seleziono e tasto destro → reset
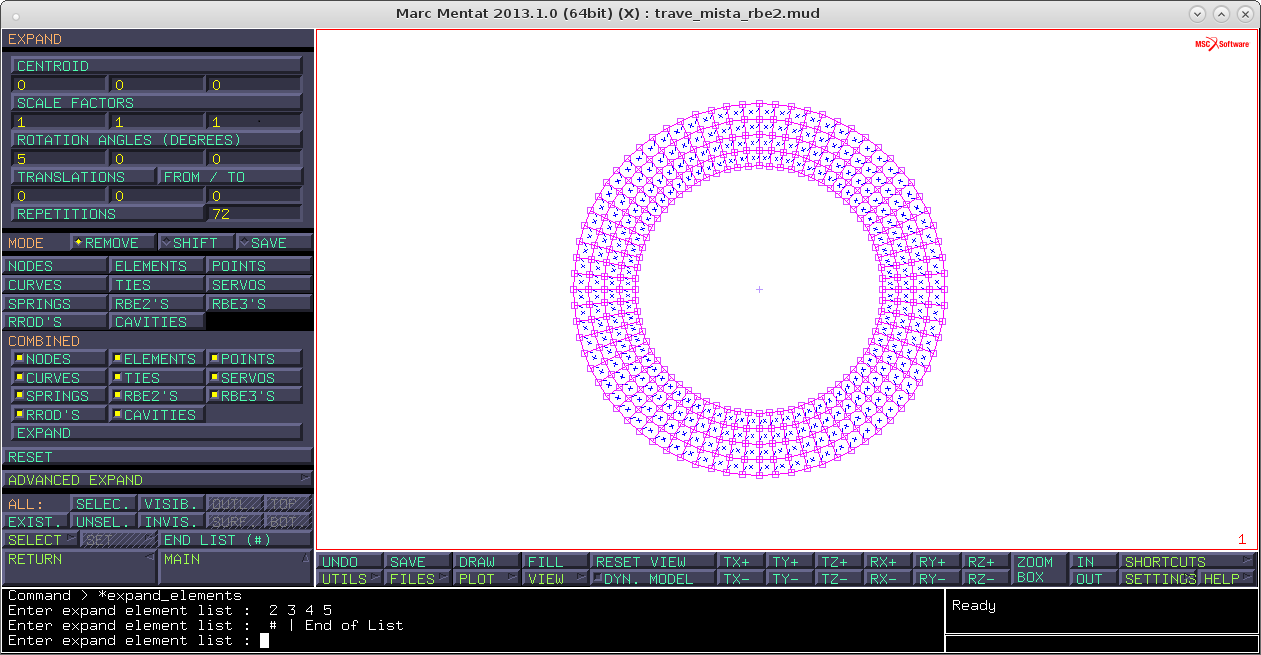
traslation 5,0,0 → repetition 100/5 =20 → elements → seleziono e tasto destro reset view → fill return → sweep → all
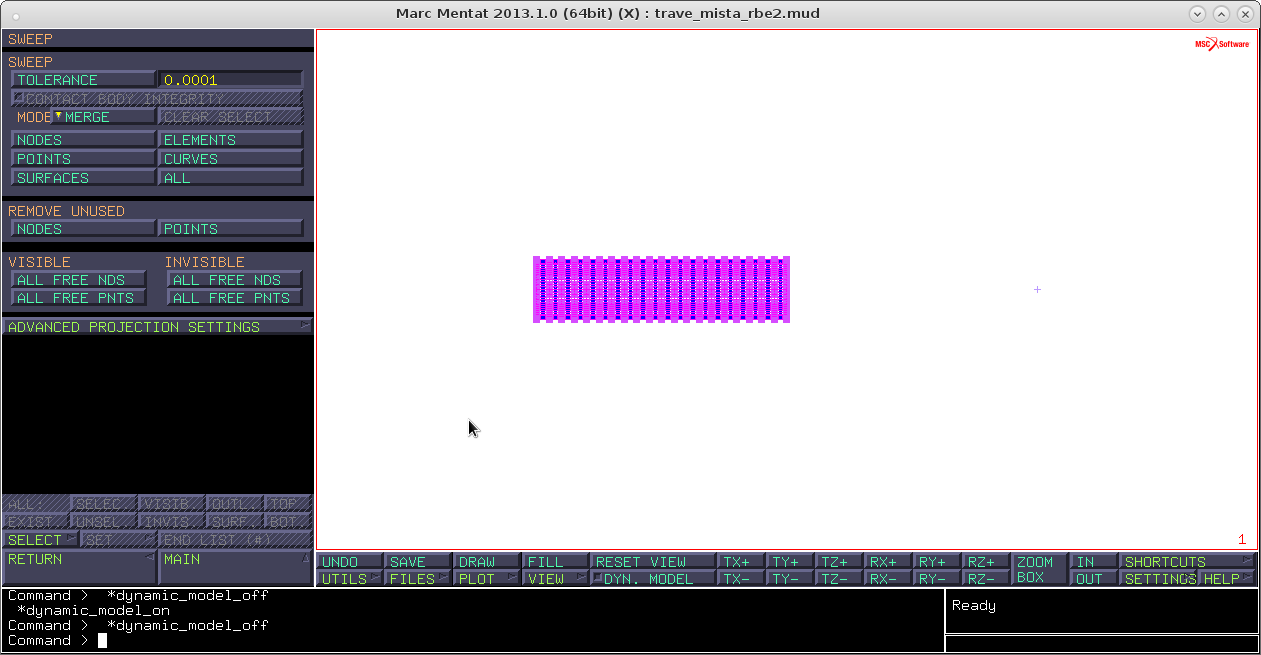
Il comando set: esso permette di raggruppare diversi elementi sotto lo stesso nome. In questo modo, agendo sul nome, rendo visibili o meno interi gruppi di elementi.
select → store (elements) → inserisco il nome (3D) → ok → seleziono tutto → tasto destro visibilitiy → none (invisibile)
Shell
Passiamo ora alla meshatura della shell, definita dal piano medio della trave.
mesh generation → node add → 100,10,0expand → reset → rotation 5,0,0 → repetitions 72 → nodes → seleziono solo il nodoexpand → reset → translation 5,0,0 → repetition 20 → elements → visibilemesh generation → sweep → nodes → visibile
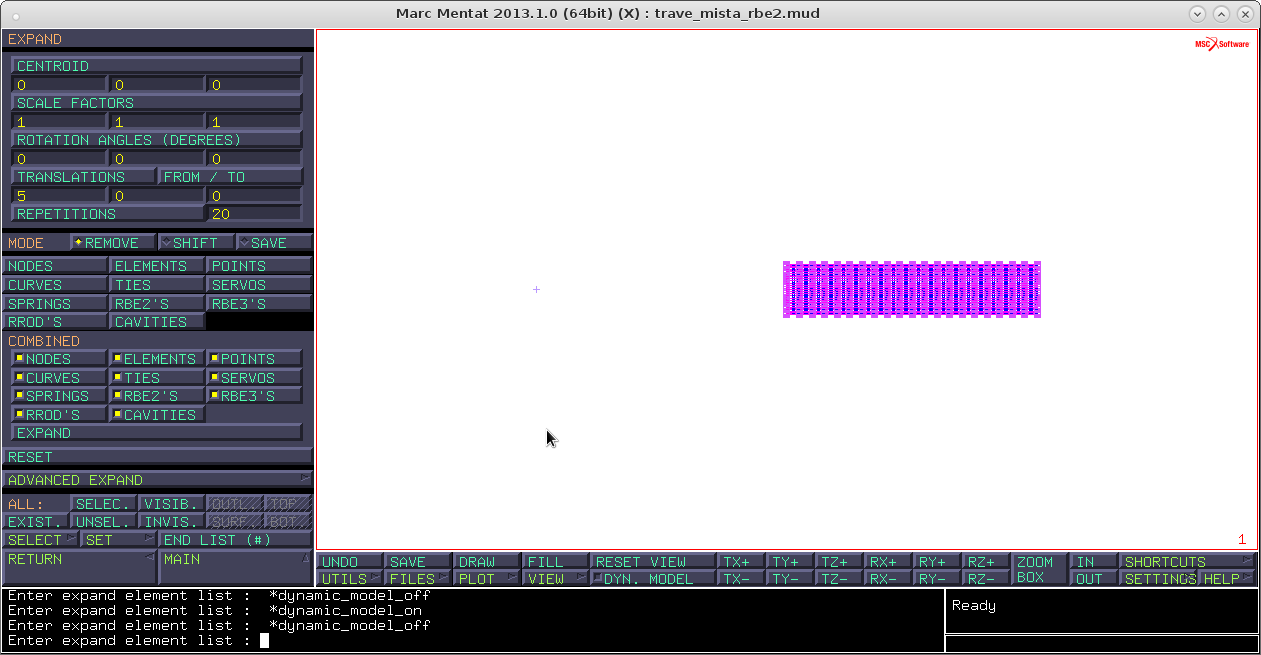
select → store (affianco a elements) → inserisco il nome (shell) → ok → visibile (a entrambi)
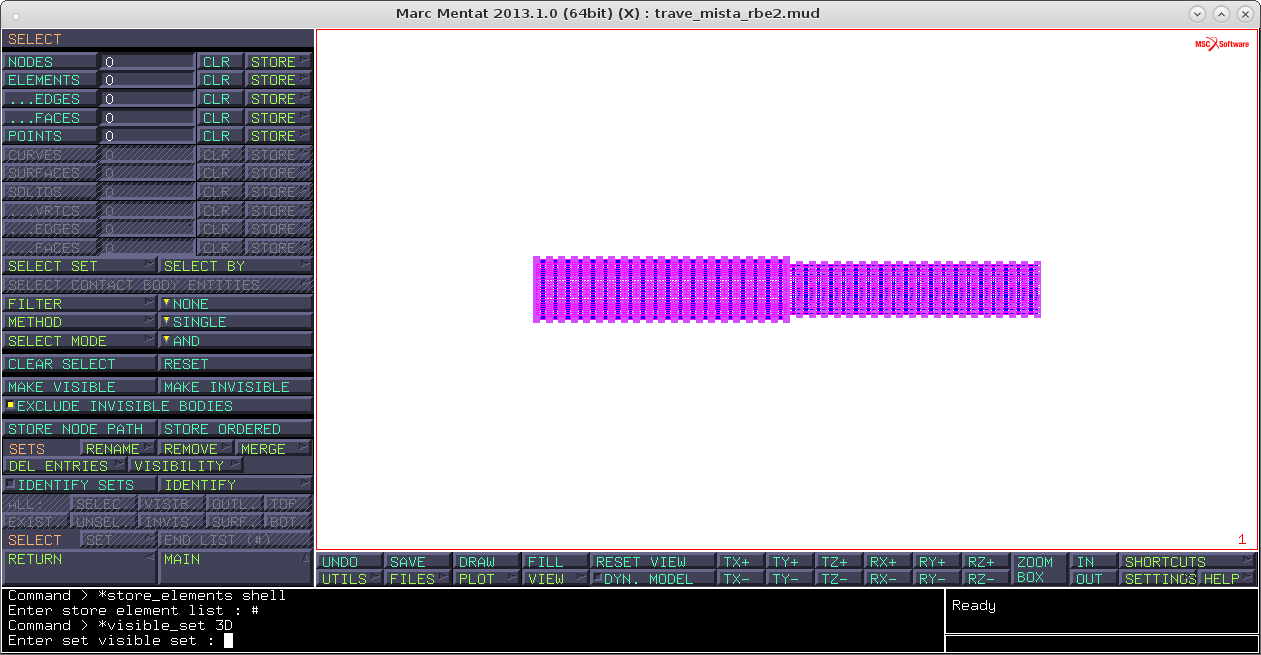
visibility → none,none (li rendo invisibili entrambi)reset view → fill
Beam
Finiamo la meshatura della trave con la parte del beam.
mesh generation → element class → line (2)mesh generation → elements add → aggiungere il beam nell'ultimo tratto a destra
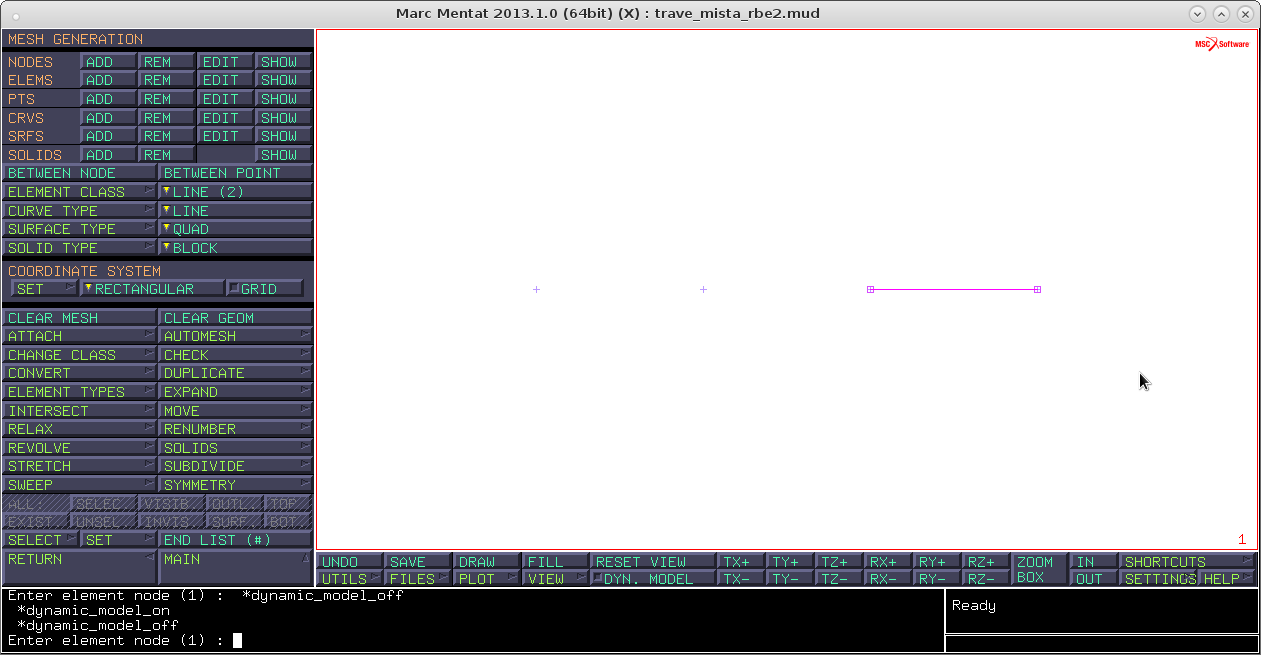
subdivide → 20,1,1 → elements → seleziono solo il beam → tasto destroreturn → sweep → nodes → visibileselect → store (elements) → inserisco il nome (line) → ok → visibilevisibility → all,all,all
Proprietà geometriche
Conclusa la meshatura, dobbiamo impostare ora le proprietà geometriche. Ovviamente per ogni tipologia di mesh l’impostazione è diversa. Ovviamente la meshatura 3D non ha bisogno di proprietà geometriche.
Beam
Partiamo col beam impostando la sezione circolare cava.
geometric proprieties → new → structural → 3D → thin-walled section beamproperties → radius 10, wall thickness 4
Nella definizione del piano locale basta non far coincidere l’asse della sezione col piano stesso. Un asse sghembo solitamente è sufficiente. Qui l’asse della trave è l’asse X, quindi lasciare 0,0,1 è sufficiente.
elements add → set → line
Shell
Passiamo alla shell definendo uno spessore di 4 mm.
new → structural → 3D → shellproperties → thickness 4 → okelements add → set → shell
Proprietà materiali
Continuiamo ora la definizione della trave impostando il materiale. La faremo in Alluminio, che ha Modulo di Young pari a 7e5 MPa e un coefficiente di Poisson di 0.3.
Material properties → material properties → new → standard → name: Alu → structural → Y.M. 70 000 , P.R. 0.3Elements add → existing
Continuità
Vediamo ora il fulcro dell’esercizio: definire la continuità tra le diverse metodologie di mesh. Creeremo un RBE2 tra il terminale del beam e la corona terminale della shell. Imposteremo il nodo reference sul nodo terminale del beam. Essendo il beam tridimensionale, attiveremo tutti i dof, in modo da passare tutti i gradi di libertà alla shell. Imporremo così moto rigido.
Main → Links → RBE2'S → retained nodes → seleziono il terminale beam → attivo tutti i dof
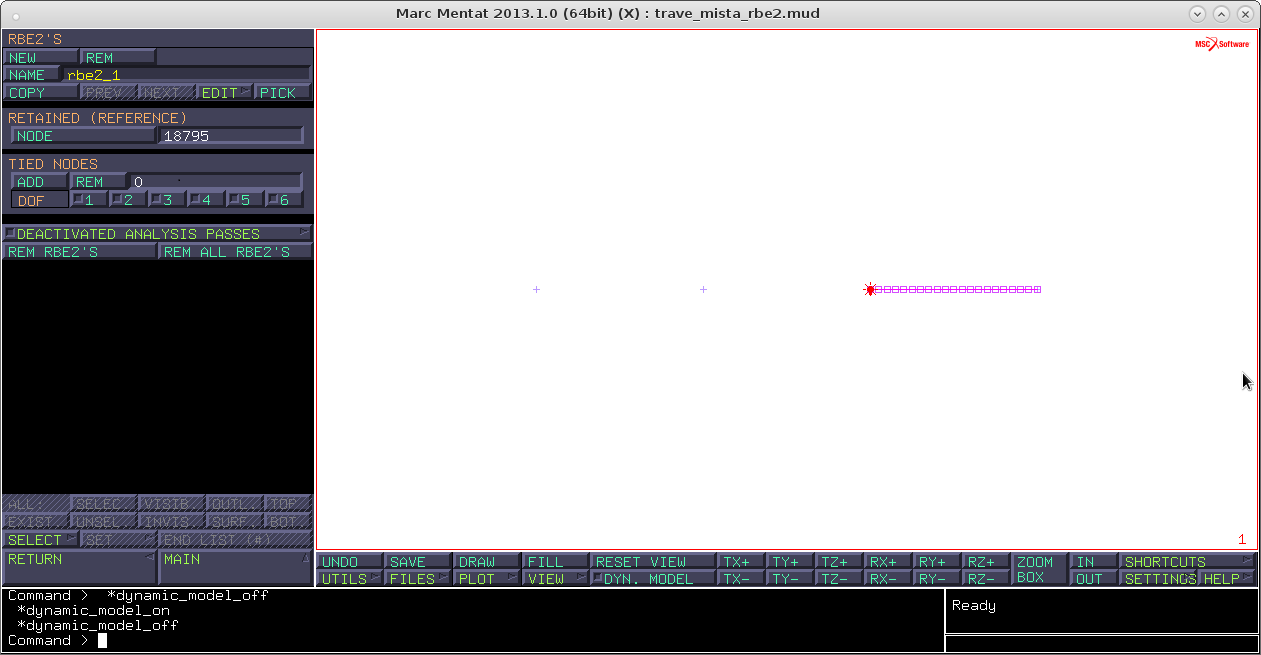
tied nodes add → seleziono la corona terminale shell → end list
È un errore definire il reference come tied di sé stesso, quindi lo rimuovo.
remove → rimuovo il nodo terminale del beam dai tides
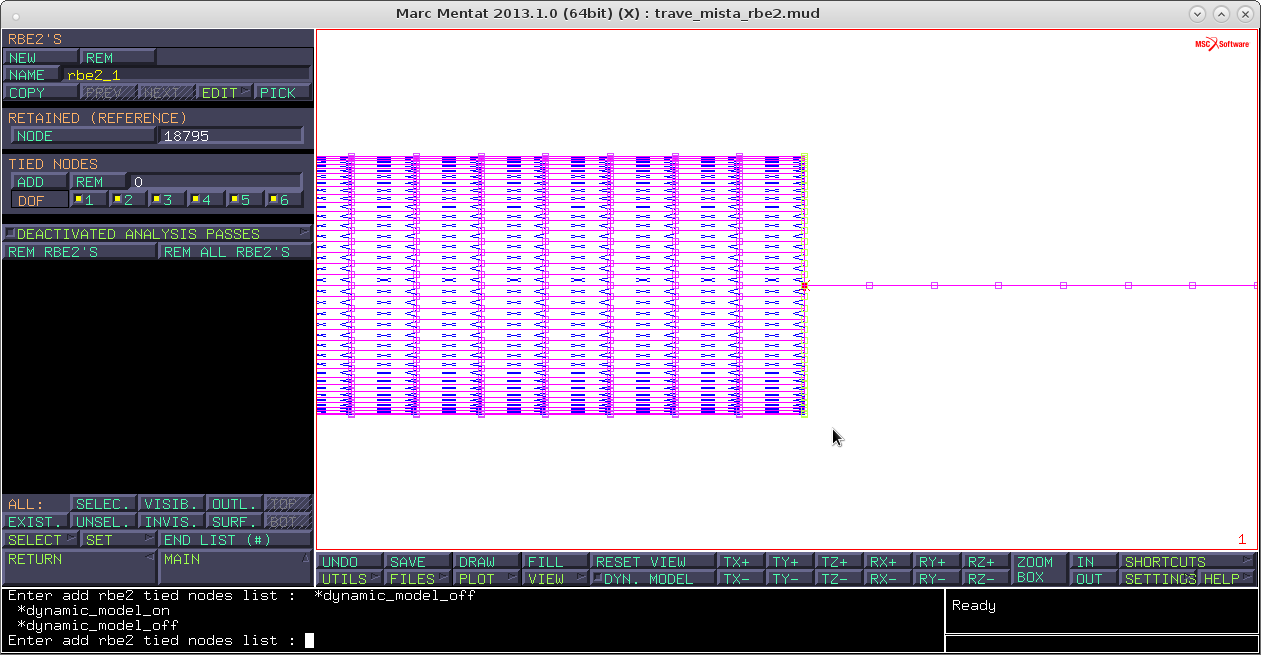
Tra la shell e la mesh 3D creo un nodo centrale che imposterò come reference. Successivamente, in modo analogo a prima, imposto i tieds che saranno i nodi estremali delle due mesh. Imposto shell e line invisibili.
mesh generation → nodes add → lo aggiungo al centro del terminale del 3D
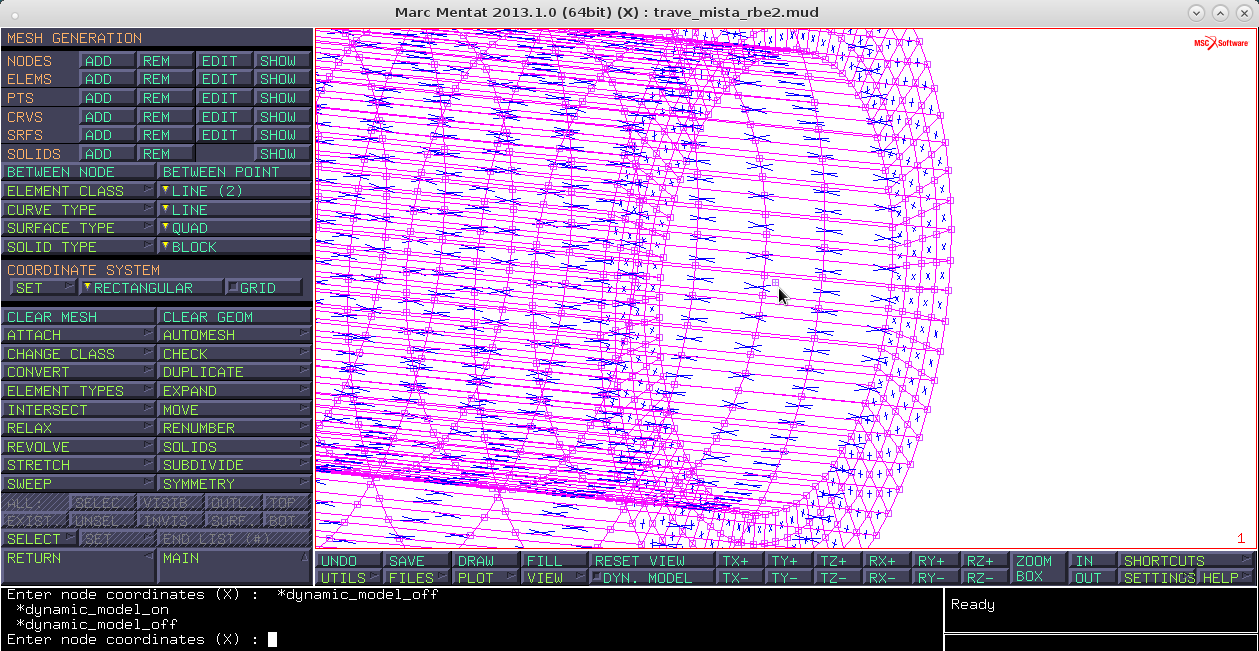
Links → RBE2'S → new → retained node e seleziono il nodo appena creato
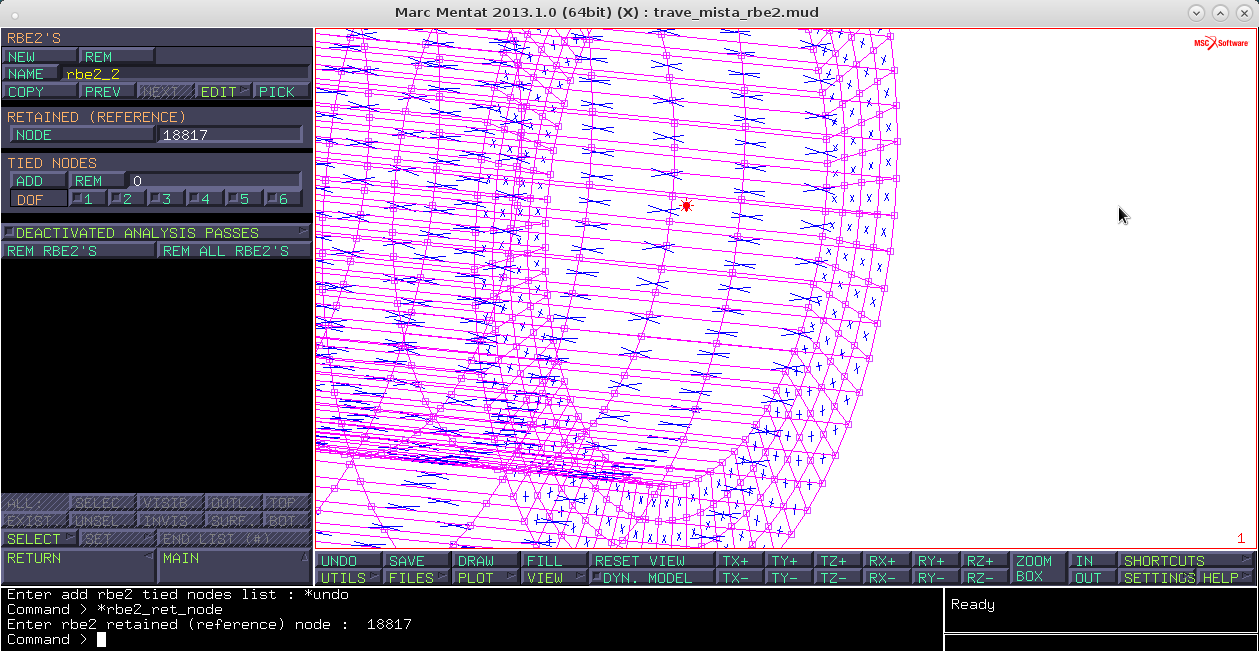
select → tutto visibile → reset view → fill → zoom box e mi avvicino all'interfaccia 3D/shellreturn → attivo tuti i dof → tieds nodes add → seleziono i nodi di interfaccia
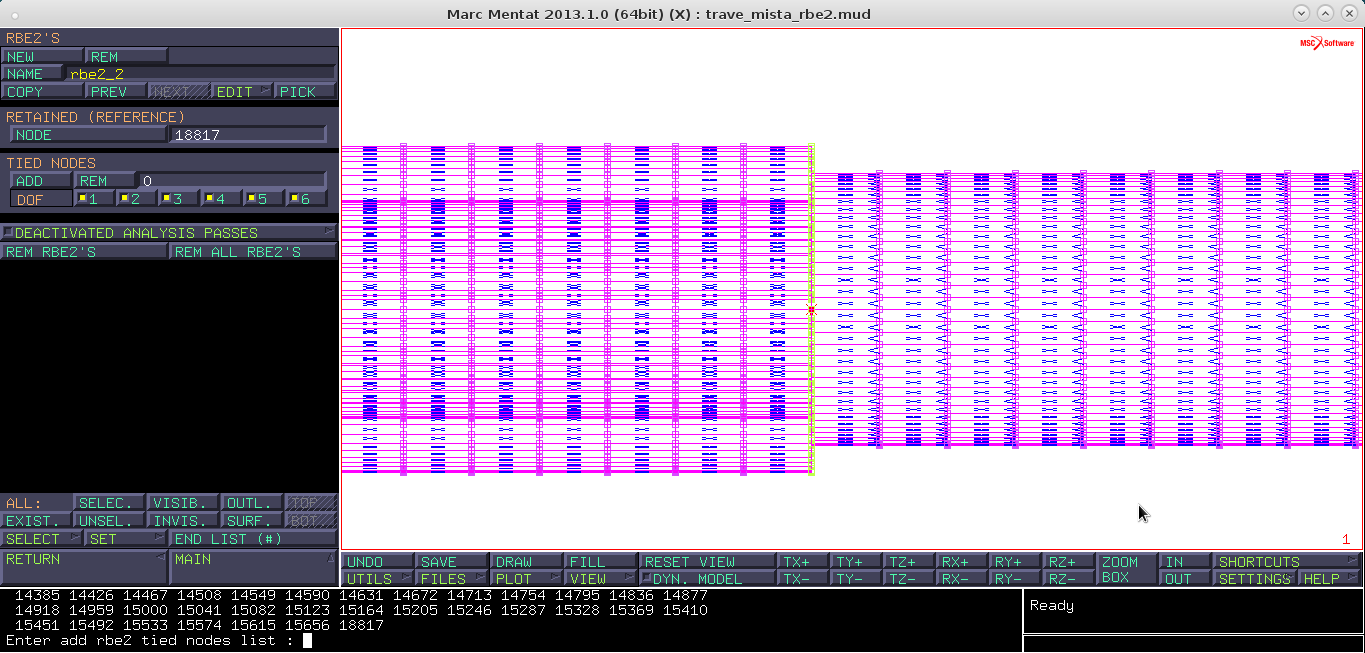
select → visibility → nascondo lo shell → aggiusto la vistareturn → remove tied → rimuovo il referencee dai tiedselect → rendo tutto visibile
Boundary Conditions
Concludiamo definendo ora l’incastro e il carico puntuale in Y di -1000 N sul beam. Essendo in 3D e lavorando solo sui nodi non ha senso bloccare le rotazioni. Infatti i bricks in 3D non hanno rotazioni.
Main menu → boundary conditions → new → Structural → fixed displacement → name: incastro → properties → displacement x,y,z 0 → oknodes add → aggiungo i nodi estremali a sinistra
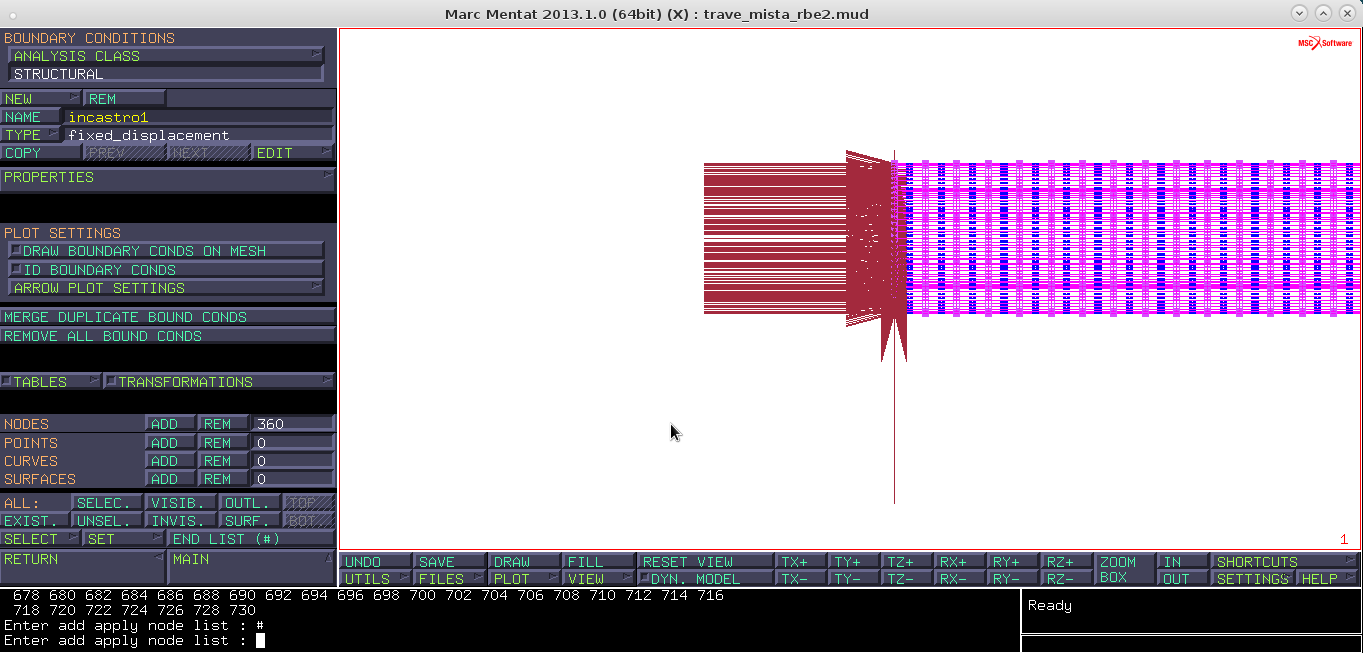
new → structural → point load → name: carico → properties → lungo Y di valore “-1000”nodes add → si aggiunge all'estremità destra
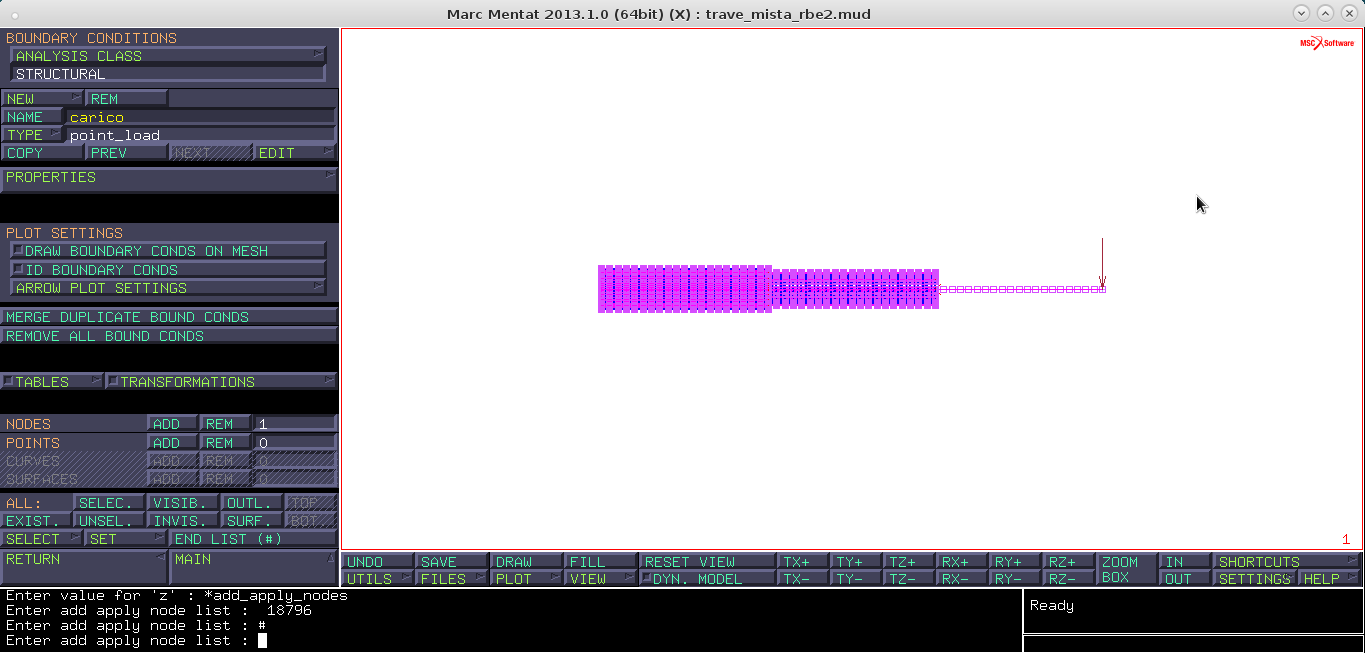
Concludiamo infine il lavoro lanciando il job.
main menu → job → new → structural → properties → job results
Selezioniamo gli sforzi che ci interessano:
- stress;
- elastic strain;
- equivalent Von Mises stress;
- praticamente tutto ciò che è “beam”.
jobs → run → submit → 3004 di exit number
Guardando i risultati (numerics) si può vedere la continuità degli sforzi nei punti di giunzione tra le varie tipologie di mesh.
main menu → results → open default → numerics
Autori e note
Autori
Cassi Tommaso mat. 104896 , Fergnani Federico mat. 105270 , Pellegrini Stefano mat. 212924
Note
Per ulteriori commenti e osservazioni sul modello iniziale dell'effetto Vlasov si rimanda alle lezioni precedenti.
Tabella di monitoraggio carico orario
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Cassi | 10 | — | — | — | — |
| Fergnani | 8 | — | — | — | — |
| Pellegrini | 12 | — | — | — | — |
| Mattia Canali | — | 1 | — | — | — |
| Vincenzo Iasevoli | — | 0.5 | — | — | — |
| Revisore 2 | — | — | — | — | — |
| Revisore 3 | — | — | — | — | — |
| Revisore 4 | — | — | — | — | — |
| Totale | — | — | — | — | — |
</hidden>
Note di revisione
PATTUME
Per utilizzare Alt nell'attivare il dynamic model occorre andare dal menu GNOME in
System Preferences Windows
e portare Movement key da Alt a Super (or “Windows logo”) prima di lanciare Mentat.
Per lanciare mentat 2013 dalle postazioni battere
mentat2013.1 -ogl -glflush
in un terminale.
Modello ad elementi finiti di riferimento
Modello postazioni inizio lezione profilo_aperto_analisi_vlasov_3d_v003.mud
“fetta” di profilo a sezione sottile aperta/chiusa a torsione con libero spostamento fuoripiano, teoria del De Saint Venant (trave infinitamente lunga, libero ingobbamento ai terminali). Attivando o disattivando la b.c. variante_sezione_chiusa_antisymm_pxz_ny impongo o meno la continuità tra il modellato e la sua immagine per antisimmetria.
Per le antisimmetrie vedi schema  , colonna a destra.
, colonna a destra.
Il modello è costruito con due piani di antisimmetria, piano zx a normale y e piano xy a normale z, ed è caricato mediante una RBE2 con parziale vincolamento dei gg.d.l. dei nodi tied/slave/dipendenti; in particolare si impone che i soli spostamenti entro piano di sezione siano comuni tra corpo deformabile e corpo rigido.
Al nodo di controllo è applicata una coppia in dir. z di 0.5 Nmm, che composta alla coppia immagine per antisymm ny impone un momento torcente di 1Nmm (unitario). All'immagine per antisymm nz del corpo rigido modellato è applicato un momento torcente uguale e contrario.
Contiene 2 jobs per sezione aperta e sezione chiusa.
Da osservare:
- la rotazione al nodo di controllo indotta dalla coppia torcente applicata (già fatto giov. scorso)
- le componenti di tensione “component 31 of stress in preferred system” con andamento lineare “a farfalla” lungo lo spessore di parte nella sezione aperta e costante nel caso di sezione chiusa (già fatto giov. scorso). Il sistema di coordinate locali è così definito
- 1: direzione entro piano di sezione lungo lo sviluppo del profilo
- 2: direzione entro piano di sezione lungo lo spessore del profilo (normale alle pareti)
- 3: direzione lungo l'asse della trave
- la presenza di spostamento z e il relativo ordine di grandezza nel caso di sezione aperta
- l'assenza di tensioni $\sigma_z$, ossia “component 33 of stress in preferred system”
I risultati di rigidezza torsionale per sezione aperta e chiusa alla de Saint Venant sono raccolti entro il foglio di calcolo; in particolare si è raccolto il dato di rotazione z al nodo di controllo della RBE2 indotta dal momento torcente unitario applicato. Nel foglio di calcolo sono pure state inserite le stime di rigidezza torsionale ottenute applicando le formule per sezioni a parete sottile aperta e chiusa; i risultati sono in linea con i dati FEM.
La rigidezza della sezione chiusa risulta ~648 volte quella della sezione aperta, a parità di materiale, area, e momento d'inerzia. Si nota che le due sezioni hanno pari comportamento a flessione.
Si può passare quindi al caso di trave a lunghezza finita (l/d=10), con d=120 mm dimensione caratteristica di sezione), aperto su di un secondo Mentat per agevolare il confronto. Tale modello è stato ottenuto dal precedente con scalatura 300% in z e con successivo subdivide in 300 suddivisioni in z.
Su questo modello si blocca il warping (spost. z) ai terminali (si impone la planarità delle sezioni, ovvero la loro natura rigida dato che il momento torcente non induce spostamenti xy entro sezione), attivando tutti i gg.d.l. nella definizione della RBE2.
I terminale di trave diventano quindi corpi rigidi, come se il profilato fosse saldato di testa a un corpo molto massivo.
Si lancia il calcolo e si osservano per la sezione aperta e chiusa le rotazioni indotte dal momento torcente unitario campione applicato; si inseriscono nel foglio di calcolo e si calcola la rigidezza torsionale della trave aperta/chiusa finita con terminali a ingobbamento (warping) ristretto. Si nota che la rigidezza del profilato a lunghezza finita, con terminali vincolati a moto di corpo rigido, è maggiore di quella prevista dal de Saint Venant per un fattore ~6 per mille nel caso di sezione sottile chiusa e di ~100 volte nel caso di sezione sottile aperta.
Si nota inoltre la presenza di tensioni “component 33 of stress in preferred system” non trascurabili nel caso a warping ristretto (confrontarli ad esempio con l'entità della comp 31), massime nell'intorno degli RBE2 e a scalare verso la mezzeria della trave.
ATTENZIONE: il picco di sigma 33 in estremità di trave è associato ad una singolarità tensionale tipica della connessione tra una struttura deformabile e una struttura rigida (indotta principalmente da strizione per effetto poisson impedita). Dalla forte discontinuità tensionale tra il primo e il secondo strato di elementi si evince la presenza di un'anomalia, che giustifichiamo con la natura singolare dello stato tensionale al punto. Le singolarità tensionali saranno trattate più approfonditamente in una lezione di teoria dedicata.
Al contempo la componente z di spostamento è nulla in estremità di trave in corrispondenza dell'RBE2 (coerentemente con warping nullo), e si accresce spostandosi verso la mezzeria, senza tuttavia raggiungere gli ordini di grandezza che ho rilevato nella fetta di trave alla De Saint Venant (vedere confronto diretto tra le due deformate amplificate di 1e6, e i fondoscala della scala cromatica).
Si verificano infine le forze trasmesse dalla RBE2 al corpo deformabile visualizzando le 'Tying forces' dal menu vector plot sia nel caso a lunghezza finita, warping impedito ai terminali che nel caso “fetta alla de Saint Venant”. In quest'ultimo caso le azioni sono entro sezione e richiamano la farfalla delle tau, nel caso a warping impedito invece sono azioni principalmente assiali, con lieve componente normale alla parete a contrastare l'espansione per effetto poisson (la parete è infatti localmente in compressione).
Si definisce “effetto Vlasov” l'aumento di rigidezza torsionale tipico delle sezioni sottili aperte associato al contrasto del libero warping delle sezioni.
Per verificare l'importanza di tale effetto su di una trave indubitabilmente snella si procede a una ulteriore scalatura di 10x in direzione z del modello che porta la trave ad un rapporto d/l=100.
Da menu mesh generation→move scalo il modello e rilancio il calcolo. Mi riservo di analizzare a posteriori l'affidabilità dei risultati in presenza di elementi fortemente allungati in z, ad esempio controllando la (dis)continuità delle tensioni in direzione z.
Da questo modello allungato osservo uno spostamento z alla mezzeria che è sì dell'ordine di quello previsto dal modello De Saint Venant, ma è comunque ancora sensibilmente minore (1.207e-4 vs 2.051e-4 mm per 1Nmm di Mt applicato). E la trave è indubitabilmente snella.
Si commenta in particolare l'apparente aumento di dimensione della sezione terminale ruotata (utilizzo anche qui un fattore di amplificazione della deformata) dovuto al fatto che la modellazione è lineare e quindi anche le rotazioni sono rappresentate in forma linearizzata, ossia i nodi si spostano lungo la tangente e non lungo la circonferenza.
Ciò è dovuto alle approssimazioni linerizzate delle funzioni trigonometriche $\sin(\theta)\approx \theta$ e $\cos(\theta)\approx 0$. Questa formulazione è tipicamente definita “in piccole rotazioni”. Le rotazioni sono effettivamente piccole, e solo amplificate diventano problematiche.
In realtà la formulazione a piccole rotazioni può essere utilizzata anche in grandi rotazioni se questa deriva tangenziale dei nodi non risulta problematica, come nella trave in oggetto. Il baricentro della trave ad esempio non risente degli spostamenti tangenziali spuri, e di solito in quel punto si campionano gli spostamenti e le rotazioni, né risentono della deriva tangenziale le deformazioni e le tensioni, che rimangono ingegneristicamente affidabili anche se la deformata perde credibilità.
Discorso diverso ad esempio nel caso di un perno di banco di albero motore che ruota entro la sua sede al supporto di banco; il sistema nasce con gioco a $\theta=0$, poi con la rotazione dell'albero il perno, nell'ipotesi linearizzata di piccole rotazioni, tende ad aumentare di diametro ricoprendo prima il gioco e poi inducendo una crescente interferenza. In questo caso la modellazione linearizzata perde interesse ingegneristico ed è necessario passare ad una modellazione in grandi rotazioni che tratti i termini trigonometrici in forma nonlineare.
raccordo a T scritto 2011/06/24
modello, carichi come da traccia, spessore parete 3 mm, materiale Alluminio (E=70000 MPa, nu=0.3, rho=2.7e-9 tonn/mm^3)
Si introduce con questo modello la modellazione a gusci (shell).
Si precisa la denominazione lastra/piastra/guscio secondo il Belluzzi.
Si introduce un sistema di riferimento locale all'elemento piastra, con direzione 3 normale e direzioni 1,2 entro piano tangente.
Si introduce l'osservazione che se la piastra è sottile le componenti di deformazione entro piano $\epsilon_1,\epsilon_2,\gamma_{12}$ variano linearmente lungo lo spessore.
Si introduce la modellazione a “segmenti rigidi” per i nodi allineati lungo lo spessore, che è compatibile con l'osservazione sulle deformazioni. Si nota che ad esempio una rotazione relativa di due segmenti affiancati induce una deformazione flessionale lineare da top a bottom.
I nodi definiscono la rototraslazione di questi “segmenti rigidi”.
Si definisco “superficie superiore, o top”, “superficie inferiore, o bottom” sulla base della numerazione dei nodi di elemento (se guardo l'elemento da sopra la superficie TOP, la numerazione appare antioraria), si introduce l' ID BACKFACES.
Si associa la formulazione “shell”, il valore di spessore (3mm) e l'offset (+1.5mm) mediante opportuna geometric property.
Chiamo superficie di riferimento quella su cui giacciono nodi ed elementi, che normalmente coincide con la superficie mediana del materiale, ma può essere differenziata operando sull'offset. Tipicamente i modellatori solidi (solidworks) esportano infatti le superfici esterne, e non le medie.
Si visualizzano gli elementi con il loro spessore dal menu PLOT→ELEMENT,Settings→RELATED PLOT SETTINGS,Shell attivando PLOT EXPANDED e PLOT OFFSETS
Decido di non utilizzare simmetrie/antisimmetrie per mantenere piena arbitrarietà delle sollecitazioni applicate.
Si duplicano per MESH GENERATION→SYMMETRY“ tutti gli elementi del modello e il nodo di controllo attorno al piano con normale 1 0 0 passante per 0 0 0; si duplicano quindi tutti gli elementi del modello rispetto al piano con normale 1 0 0 passante per 0 0 0''. Segue sweep.
Imposto materiale Alluminio.
Procedo quindi a creare 3 RBE2 sui terminali di trave, per poter più agevolmente applicare le azioni esterne. Osservo che queste RBE2 non perturbano la soluzione a trave nel caso di momento torcente applicato, e perturbano la soluzione per “solo” impedimento della strizione per effetto Poisson a sforzo normale e flessione. Valuterò a posteriori Tying Forces e stato tensionale nell'intorno della RBE2.
Procedo nel caso ad incastrare il nodo di controllo della trave innestata ed ad applicare un momento flettente ad uno dei terminali della trave corrente. Nella lezione di oggi ho inserito una sola RBE2, ma tu puoi andare avanti fino a fine modellazione, casomai analizzando i risultati con opzione “Out & mid” ecc ecc ecc.