Richiami di teoria della trave

Si definisce “trave” un solido geometrico con una dimensione preponderante rispetto alle altre; la teoria che permette di definire lo stato tensionale della stessa, detta teoria della trave, si basa sulle seguenti ipotesi:

• Materiale isotropo omogeneo e elastico lineare;
  
• Trave in equilibrio nello spazio e in assenza di vincoli;
  
• Assenza di forze di volume (in particolare la forza peso) e forze di superficie applicate soltanto alle facce estremali [σ_x=σ_y=τ_xy=0];
• Sezioni piane e che restano tali;
  

Il corpo così decritto presenta 6 gradi di libertà di cui tre traslazioni e tre rotazioni attorno a tre assi coordinati. Nei casi applicativi, invece, è limitato nei suoi spostamenti tramite la presenza di vincoli. Quest’ultimi interagiscono con il corpo attraverso reazioni vincolari che sottraggono gradi di libertà.
Esempi di vincolo nel piano sono:

• Cerniera: Vincolo doppio che impedisce lo spostamento del punto vincolato lungo una qualsiasi direzione del piano del problema, consentendo la rotazione;
• Incastro: Vincolo triplo che limita tutti i possibili moti del punto vincolato;
• Carrello: Vincolo semplice che impedisce lo spostamento lungo l’asse del carrello;
  

Altri tipologie di vincolo possono essere ottenute tramite la combinazione di quest’ultimi (doppio pendolo, biella, ecc.).
Un solido vincolato subisce forze e momenti dall’esterno e ristabilisce l’equilibrio in ogni sezione grazie alla nascita di reazioni interne. Tali reazioni si dividono in:

• Sforzo normale: Componente risultante esercitata lungo l’asse z, solitamente scelto come asse longitudinale della trave;
• Taglio: Componente ortogonale all’asse baricentrico;
• Momento flettente: Momento applicato con direzione ortogonale all’asse della trave;
• Momento torcente: Momento applicato con direzione parallela all’asse della trave;

La distribuzione di queste sollecitazioni sulle sezioni causa uno stato tensionale responsabile di deformazioni ed eventuali rotture. Le caratteristiche delle sollecitazioni sono indipendenti dalla sezione e dal materiale, se la struttura è isostatica ossia i gradi di vincolo coincidono con i gradi di libertà. Consideriamo il seguente esempio:

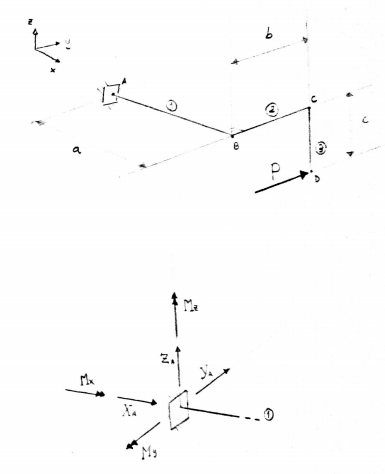
Per risolvere la struttura in figura si inizia imponendo l'equilibrio alla traslazione e alla rotazione nei sei possibili gradi di libertà dello spazio; in particolare si ha che all'incastro sono presenti tre forze dirette lungo gli assi: X_A,Y_A,Z_A quindi:

$$ \left\{\begin{matrix} &X_{A} = 0 & \\ &Y_{A}+P=0 & \\ &Z_{A}=0 & \end{matrix}\right. $$
da cui ricaviamo Y_A=-P.
Allo stesso modo all'incastro sono applicati anche tre momenti resistenti attorno agli assi coordinati, M_x,M_y,M_z e, come sopra, imponiamo l'equilibrio alla rotazione, scegliendo un generico punto, nel nostro caso A, per cui otteniamo:
$$ \left\{\begin{matrix} &P\cdot c \ + M_{x} = 0 & \\ &M_{y}=0 & \\ &P\cdot a \ + M_{z} = 0 & \end{matrix}\right. $$ da cui ricaviamo i valori:
$$ -P\cdot c = M_{x} $$ $$ -P\cdot a = M_{z} $$ a questo punto la struttura può dirsi in equilibrio.

Controlla fibre tese Mf!!

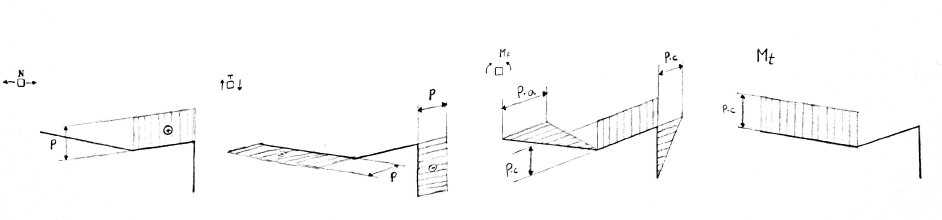
Per determinare le sollecitazioni interne, prendiamo in considerazione il tratto 3 di trave, su cui agisce il carico P; esso provoca uno sforzo di taglio negativo di entità P e un momento flettente che agisce attorno all'asse x, crescente lungo l'asse della trave e di valore massimo pari a P⋅c, che raggiunge all'intersezione con la trave 2 (punto C).
Consideriamo, ora, il secondo tratto di trave: su di esso si scarica il momento flettente di cui sopra, P⋅c, il quale resta costante lungo tutta la lunghezza b della trave; inoltre anche il carico P si scarica sotto forma di sforzo normale trattivo e dunque positivo, di entità P.
Per quanto riguarda la trave 1, su di essa il momento flettente P⋅c diventa torcente perché applicato attorno all'asse x e come tale resta costante lungo tutta la lunghezza a per poi annullarsi in corrispondenza dell'incastro (punto A), laddove è presente la reazione M_x, uguale e opposta.
D'altra parte il carico P, pensato applicato all'estremità B della trave 1, genera un momento flettente attorno a z, crescente lungo la stessa fino al valore P⋅a che si ottiene all'incastro, dove anch'esso viene bilanciato dal momento M_z ivi presente. La forza P, inoltre, produce un taglio costante, di entità -P, che in presenza del vincolo viene eliminato dalla reazione Y_A.
Nelle figure seguenti è possibile notare l'andamento delle sollecitazioni interne lungo la :

Dato il seguente telaio semplificato, è definito il sistema di riferimento considerando come asse strada, l’asse X, asse Y parallelo al piano stradale e asse Z ortogonale ai precedenti.

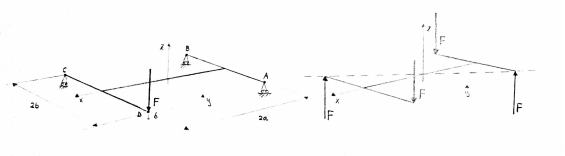
Tale sistema è labile nello spazio in quanto i vincoli eliminano 3 gradi di libertà rispetto i 6 totali poiché ogni carrello impedisce solo il moto lungo l’asse Z.
Dal punto di vista delle sollecitazioni indotte nel materiale ciò è irrilevante perché non vi sono carichi nelle direzioni di possibile moto.
Al fine di rendere tale struttura isostatica è possibile introdurre una cerniera in qualsiasi punto in modo da impedire i moti liberi (traslazione in x, y e rotazione intorno all’asse z), tuttavia tale vincolo non introduce alcuna reazione vincolare rispetto la situazione precedente; risulterebbe scarico in quanto lungo quelle direzioni non ci sono carichi applicati da indurre spostamenti.
Attraverso considerazioni di equilibrio alla rotazione, è possibile ricavare le reazioni vincolari lungo Z; per equilibrio attorno alla diagonale AC la reazione vincolare nel nodo B è pari in modulo e verso del carico P. Per medesime considerazioni di equilibrio lungo il segmento CD la reazione vincolare nel nodo C ha modulo pari a P e verso opposto al carico applicato. Per concludere l’analisi statica la reazione vincolare nel nodo A ha modulo pari a al carico e verso opposto.
La struttura è geometricamente simmetrica ma la distribuzione dei vincoli non lo è, tuttavia sostituendo a quest’ultimi le rispettive reazioni vincolari la distribuzione dei carichi risulta antisimmetrica.
L’antisimmetria può essere definita a partire dal concetto di simmetria; invertendo forze e momenti da un solo lato del piano di simmetria di una struttura antisimmetrica, questa diventa simmetrica.
Riferendosi al problema in questione la struttura presenta 3 piani di antisimmetria rispetto la distribuzione dei carichi di cui XZ perpendicolare all’asse Y, XY perpendicolare all’asse Z e il piano ZY ortogonale all’asse X.
In presenza di antisimmetria posso studiare parte della struttura perché il resto sarà derivabile tramite le regole dell’antissimetria.
Tagliando la struttura è possibile sostituire ad una delle due parti dei vincoli i quali eviteranno spostamenti o/e rotazioni incompatibili con la presenza della porzione di corpo mancante.

Regole di sostituzione dei vincoli:
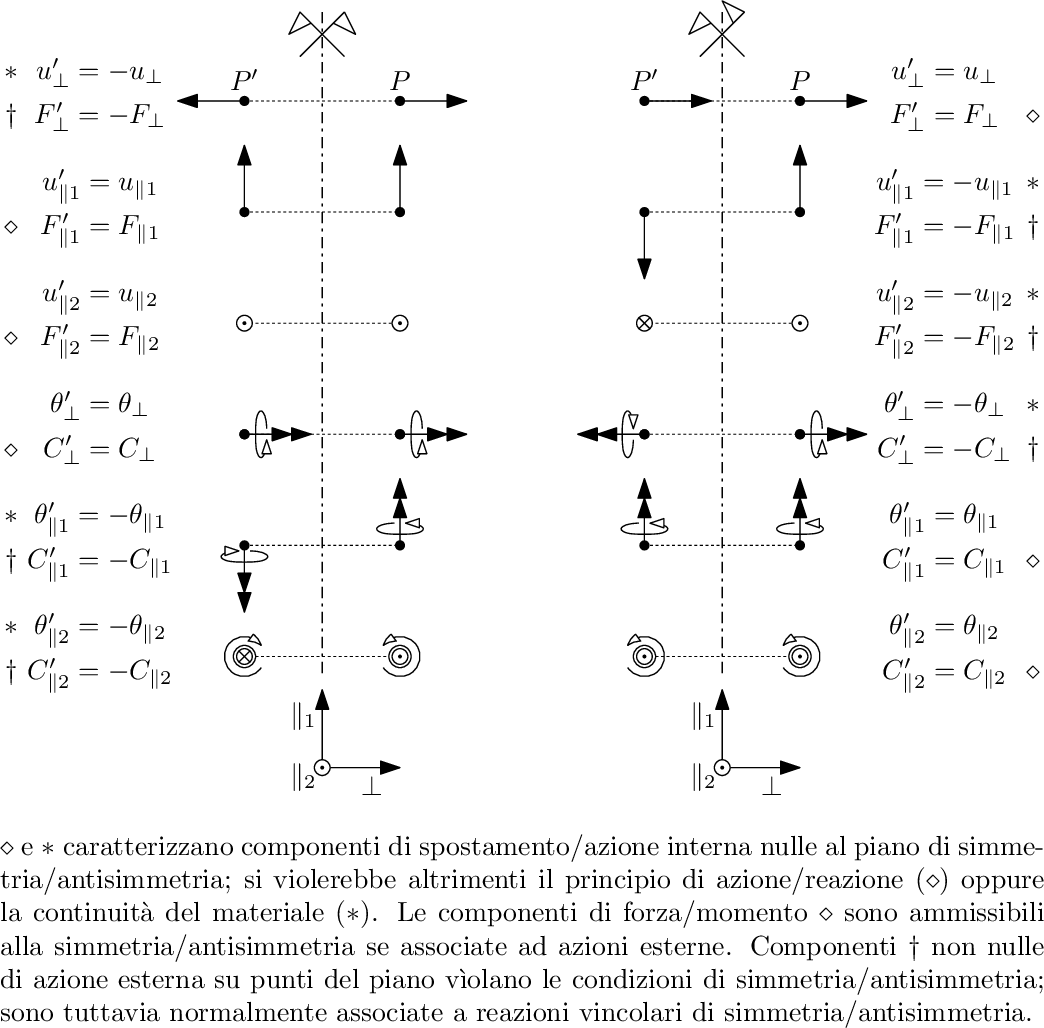
Gli spostamenti consentiti per figure attraversate da un piano di simmetria o di anti-simmetria sono tutti quelli che non comportano una separazione o compenetrazione tra le parti in cui è divisa la struttura, ossia lasciano in contatto i punti che lo erano precedentemente. Immaginiamo una trave tagliata da un piano di simmetria o antisimmetria x,y con normale z e consideriamo i diversi spostamenti a cui è soggetta la superficie di contatto:

Traslazione lungo l'asse z, normale al piano:
Per una struttura simmetrica, tale spostamento comporta la separazione tra le parti della trave, che risulterebbe soggetta a due forze di verso opposto, pertanto non è consentito; viceversa per una struttura antisimmetrica, la traslazione è ammessa in quanto le due parti della trave sono, soggette a forze nello stesso verso.

Traslazione lungo l'asse y, giacente sul piano:
Per una struttura simmetrica lo spostamento di una parte in direzione y comporta uno spostamento nello stesso verso della parte restante, pertanto tale movimento è consentito; viceversa, per una struttura antisimmetrica, lo spostamento di cui sopra comporterebbe una traslazione in verso opposto tra le parti, quindi non è ammesso.

Traslazione lungo l'asse x, giacente sul piano:
Analogamente al caso precedente, per una struttura simmetrica a uno spostamento in direzione x corrisponde un movimento nello stesso verso delle parti, dunque è ammesso; d'altro canto per una struttura antisimmetrica, tale movimento non è consentito poiché comporta uno scostamento in versi opposti delle due metà, con evidente separazione del materiale.

Rotazione attorno all'asse z, normale al piano:
Tale rotazione, per una struttura simmetrica, é consentita, in quanto le due parti ruoterebbero nello stesso verso; viceversa questa rotazione non è ammessa nel caso di travi antisimmetriche.

Rotazione attorno all'asse y, giacente sul piano:
Per una struttura simmetrica un simile movimento non è consentito perché i due tronconi in cui è divisa la trave ruoterebbero in versi opposti con conseguente rottura della trave originaria; per strutture antisimmetriche, invece, è uno spostamento ammesso.

Rotazione attorno all'asse x, giacente sul piano:
Una rotazione attorno all'asse x comporta, per la struttura simmetrica, contemporaneamente una compenetrazione e un distacco delle superfici originariamente a contatto e dunque risulta non essere consentito; nel caso di una struttura antisimmetrica, tale rotazione è ammessa, poiché le due parti ruotano nello stesso verso.

Con riferimento alla tabella di figura, la struttura simmetrica consente traslazione lungo gli assi x e y e rotazioni attorno all'asse z; la struttura antisimmetrica, invece ha tali movimenti bloccati e viceversa consente la traslazione lungo l'asse z e le rotazioni attorno agli assi x e y.