Indice
Azione di taglio su una trave costituita da due parti
Azione tangenziale e normale (parte 1 e 2)
Si consideri una trave che, anziché essere costituita da un unico elemento, è caratterizzata dalla sovrapposizione di due elementi identici per forma geometrica e dimensioni. Si consideri inoltre una forza $\mathit{P}$ con direzione ortogonale alla trave e applicata in mezzeria sull’elemento superiore, come rappresentato in figura.
La trave è vincolata con una cerniera ed un carrello a terra che generano entrambi una forza di reazione diretta verticalmente di entità $\mathit{\frac{P}{2}}$. Le dimensioni della trave sono: $\mathit{l}$ per la lunghezza, $\mathit{h}$ per l’altezza dell’intera trave, $\mathit{\frac{h}{2}}$ per l’altezza di ciascuno dei due componenti e $\mathit{b}$ lo spessore della trave (non rappresentato in figura). La trave così costituita risulta in generale meno rigida di una trave realizzata in un unico pezzo poiché, se i due elementi risultano semplicemente appoggiati l’uno sull’altro, non si ha trasmissione del taglio e la freccia di deformazione in mezzeria risulterà superiore alla trave realizzata di pezzo. Invece se si interpone tra le due parti della trave uno strato infinitesimo di colla, o le si imbullona tra loro, la rigidezza diventa paragonabile a quella della trave in un pezzo unico. Questo perché la colla è in grado di trasmettere il taglio e la giunzione delle due metà con bulloni consente di creare una distribuzione di pressione (che può essere ritenuta uniforme) tra le due superfici di contatto. La pressione comporta lo sviluppo di forze di attrito radente su tali superfici che rappresentano proprio il mezzo di trasmissione del taglio tra i due elementi. Si supponga di avere una trave capace di trasmettere il taglio tra i due elementi. Si determini ora l’entità della distribuzione dell’azione tangenziale alle superfici di contatto tra le due parti, che sarà uniforme. Si consideri solo metà della trave di partenza poiché è possibile individuare un piano di simmetria che divide a metà l’intera trave.
Come si può vedere dalla figura, l’intera sezione di mezzeria della trave risulta caricata da una distribuzione a farfalla di $\sigma _{f}$, il cui valore massimo può essere determinato da quello del momento flettente in tale sezione.
$M_{f}= \frac{P}{2}\ast \frac{l}{2}$
da cui
$\sigma_{f}= \frac{P\ast l }{4}\ast \frac{6}{b\ast h^{2}}$
Si consideri ora solo una delle due parti di cui la trave è costituita. È possibile rappresentare il carico agente sulla sua sezione come la sovrapposizione di una distribuzione uniforme di $\frac{\sigma _{f}}{2}$ e di una a farfalla di entità massima $\frac{\sigma _{f}}{2}$, come nella figura di seguito.
L’azione assiale risultante di tali distribuzioni deve essere necessariamente equilibrata da una distribuzione di $\tau$ sulla superficie di contatto tra i due elementi della trave e questa azione tangenziale alle superfici può essere ritenuta uniforme e calcolata tramite l’equilibrio.
$\frac{\sigma _{f}}{2}\ast b\ast \frac{h}{2}= \tau \ast \frac{l}{2}\ast b$
Esplicitando $\tau$ in tale relazione e sostituendovi l’espressione di $\sigma _{f}$ si ottiene:
$\tau = \frac{\frac{P}{2}}{b\ast h}\ast \frac{3}{2}$
Individuato il valore di $\tau$ è possibile confrontarlo con la massima azione di taglio ammissibile da un incollaggio o con il massimo valore della forza d’attrito ottenibile tra le superfici in caso di giunzione con bulloni (funzione della pressione agente tra esse). Si può così verificare la reale capacità della trave di trasmettere il taglio, ripartendo il carico tra i due elementi. Vogliamo ora individuare l’azione ortogonale alle due superfici di contatto dei due elementi di trave. Su tali superfici agisce la pressione dell’eventuale giunzione con bulloni utilizzata per unire le due parti. Tale pressione non deve essere considerata come componente dell’azione cercata, poiché non è dovuta al carico di taglio P cui l’intera trave è soggetta. Bisogna invece capire come il taglio P si ripartisce tra le due parti della trave. Infatti, se si conosce la porzione di taglio agente su ciascuna componente della trave, essa risulta distribuita uniformemente su tutto l’elemento e ortogonate alla superficie di contatto.
Il taglio agente su ogni elemento della trave deve essere tale da garantire la continuità del materiale nella condizione deformata. Se si considera sempre metà trave e si ripartisce il taglio in modo che sia $\mathit{\frac{P}{2}}$ sull’elemento superiore e nullo sull’elemento inferiore, la deformazione risultante genererebbe compenetrazione del materiale, e quindi questa no può essere la reale ripartizione del taglio $\mathit{\frac{P}{2}}$ agente su ciascuna metà della trave. Si può verificare che la reale ripartizione del taglio vede agire una forza pari a $\mathit{\frac{P}{4}}$ su ciascun elemento della trave, che risulta quindi l’azione di taglio agente su ogni elemento della struttura considerata (si considerino sempre tutte le forze applicate sulla sezione della trave). Il taglio $\mathit{\frac{P}{2}}$ si ripartisce quindi esattamente a metà tra i due elementi della trave, condizione che garantisce la continuità del materiale nella condizione deformata.
Consideriamo la trave superiore per controllare come si deforma. È presente un’azione tagliante dovuta all’incollaggio nella parte inferiore. Trasportandola sull’asse baricentrico diventa un carico assiale distribuito equilibrato da $N$; però per far questo si genera una coppia di trasporto, che è una coppia distribuita, il cui valore può essere ricavato imponendo l’equilibrio alla rotazione:
$$c\cdot dl=\tau \cdot b\cdot dl\cdot \frac{h}{4} \rightarrow c=\tau \cdot b\cdot \frac{h}{4}$$
Quindi nella parte superiore della trave agiscono le seguenti forze:
dove $$M_{f}=\frac{\sigma _{f}}{2}\cdot \frac{b\cdot \left ( \frac{h}{2} \right )^{2}}{6}$$
$$N=\frac{\sigma _{f}}{2}\cdot b\cdot \frac{h}{2}$$
Mentre in quella inferiore le azioni assiali sono uguali e contrarie mentre la coppia distribuita e il momento flettente sono gli stessi. Perciò, essendo le deformazioni assiali uguali e contrarie, le due parti di trave non si accorciano e allungano allo stesso modo; tuttavia saranno nulli gli spostamenti in direzione assiale all’interfaccia delle due travi perché sia nella parte inferiore della trave superiore che nella parte superiore della trave inferiore le tensioni generate da $N$ e $\ M_{f}$ sono uguali e contrarie.
Per il calcolo degli spostamenti trasversali $N$ può essere trascurata in quanto non è influente. In questo modo ottengo sforzi identici nella trave sopra e in quella sotto avendo queste stessa sezione, stesso carico e stesse condizioni al contorno di spostamento indotto; quindi, di conseguenza, le due travi avranno punto per punto lo stesso identico abbassamento e reazione, il che vuol dire stessa deformata e stessa modalità di cedimento. Per cui se abbiamo due travi, queste, si dividono i carichi applicati. Le considerazioni fatte valgono sia per le deformate puramente flessionali che per quelle flesso-taglianti. Se invece che garantire la trasmissione del $\tau$ con l’incollaggio mettessimo, ad esempio, un appoggio lubrificato verrebbero a mancare le coppie concentrate e le azioni di sforzo assiale distribuito e verrebbero trasmessi solo i carichi concentrati:
Si può verificare che se $J$ è il momento di inerzia della sezione originale, allora $J$ della trave composta sarà diverso in base al tipo di collegamento:
$$\left\{\begin{matrix} J=\frac{b\cdot h^{3}}{12} \rightarrow travi\, unite\\ \\ J=2\cdot \frac{b\cdot \left ( \frac{h}{2} \right )^{3}}{12} \,=\, \frac{b \cdot h^{3}}{48}\rightarrow travi\; divise \end{matrix}\right.$$
Stato tensionale in travi soggette a Taglio e Momento torcente
Sezioni specifiche (parte 3)
Si consideri una sezione sottile aperta a C di spessore uniforme. Per ricavare le $\tau$ taglianti si parte dalla farfalla flessionale sulla sezione. Si tracciano gli assi locali $x$ e $y$ a partire dal baricentro della sezione e si suppone che sia applicata una forza di taglio $T_{y}$ in direzione $y$.
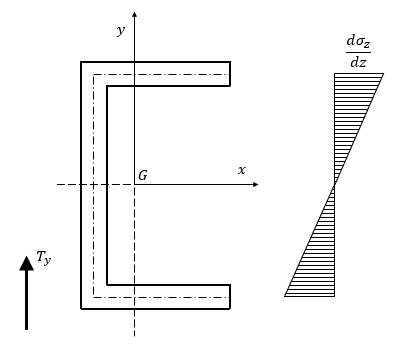
La sezione ha un asse di simmetria $x$, che è quindi anche asse principale di inerzia e $J_{xy}= 0$. $\sigma_{z}$ è uniforme su tutti i punti disposti su rette poste ad una certa distanza dall’asse di simmetria. La costruzione grafica sul piano è rappresentativa, in questo particolare caso di pura curvatura attorno all’asse $x$. Se così non fosse, la farfalla flessionale varierebbe entro piano e fuori piano anziché essere piana. Facendo considerazioni di equilibrio su ogni concio di struttura, si integra $\frac{d\sigma_{z}}{dz}$ su aree via via crescenti e si trovano le tensioni taglianti per ogni punto della struttura.
$$\overline{\tau }\cdot t=\iint_{A^\star}\frac{d \sigma_z}{dz} d A$$
Nei punti terminali le $\tau$ si annullano perché si calcola il momento del primo ordine su un sistema baricentrico.
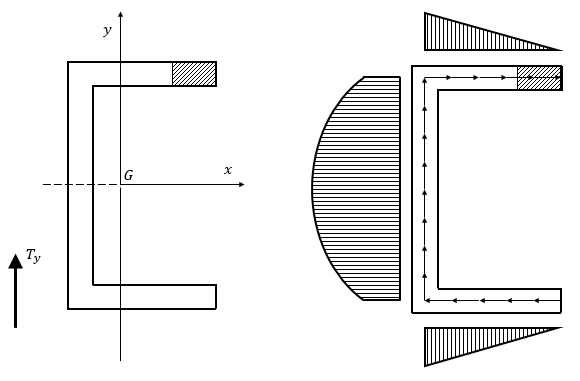
La distribuzione di $\tau$ non può che essere quella in figura, perché definita dall’equilibrio su ogni concio secondo la formula di Jourawski. Tutti gli sforzi di taglio $\tau$ agenti su un ramo della sezione a C hanno la stessa retta d’azione e possono essere sommati ottenendo forze cumulative rappresentate graficamente nella figura sottostante.
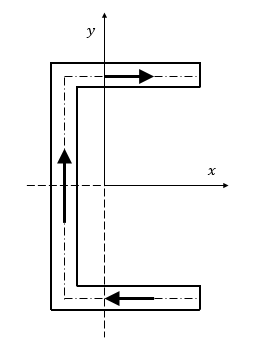
La risultante verticale (in direzione $y$) di tutte le azioni è uguale al taglio applicato $T_{y}$, mentre le forze orizzontali che si sviluppano sono forze indotte dal taglio. Considerando il taglio applicato al baricentro, la distribuzione delle forze nella figura di prima non sarebbe staticamente equivalente a questo caso particolare. La risultante verticale è la medesima nei due casi, ma gli sforzi $\tau$ agenti sui rami estremi della sezione a C generano coppia. Dunque la forza di taglio $T_{y}$ non può essere considerata applicata nel baricentro al fine di ottenere la distribuzione di figura. Una volta trovati gli sforzi di taglio tau con la formula di Jourawski, si può individuare il punto in cui applicare la forza di taglio, attraverso considerazioni di equilibrio alla rotazione. Il taglio è applicato in direzione $y$, ma il parametro da ricavare è la distanza d fra un punto di riferimento e la retta d’azione del taglio stesso. Scegliendo come punto di riferimento il baricentro, si ricava il momento dato dagli sforzi di taglio rispetto a questo (coppia $M$ associata agli sforzi $\tau$). Si trova d imponendo:
$$ M_{\tau}=d\cdot T_{y}$$
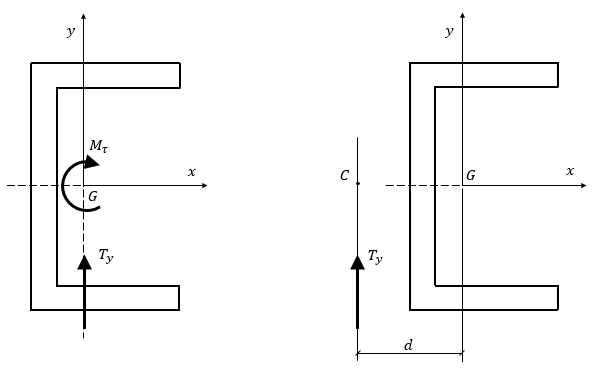
La distanza d denota la posizione di un punto $C$, detto centro di taglio, tale che se il taglio ha retta d’azione passante per $C$, allora genera le tensioni trovate attraverso la formula di Jourawski.
Le condizioni per cui:
- $\sigma _{z}\neq 0$
- $\sigma _{x}=\sigma_{y}=\tau _{xy}=0 $
- $\tau_{zx}=\tau_{yz}=0 $
non è detto che siano verificate nel caso multimateriale: il modulo di Young $E$ può variare, ma è necessario che il modulo di Poisson $\nu$ sia omogeneo nella sezione affinché queste relazioni siano valide. Tutti i metalli hanno modulo di Poisson $\nu \approx 0,3$, per cui il vincolo è rispettato anche con metalli diversi nella stessa sezione. Un secondo vincolo è che il materiale sia isotropo; in alcuni casi anche un materiale ortotropo con asse di ortotropia allineato con la trave rispetta lo stato tensionale.
Torsione in sezione sottile chiusa
Nel caso di torsione in sezione sottile chiusa, si assume che le $\tau$ siano uniformi lungo lo spessore della parete (nelle sezioni sottili aperte invece si assume che l’andamento delle tensioni $\tau$ da torsione vari linearmente nello spessore). Consideriamo una porzione di sezione sottile chiusa a spessore non uniforme soggetta a momento torcente.
Nell’ipotesi che $\sigma_{z} = 0$, l’equilibrio alla traslazione è: $$t _{1}\,\tau _{1} = t _{2}\,\tau _{2}$$ Poiché questa relazione è valida per ogni sezione 1 e 2 della sezione iniziale, definita un’ascissa curvilinea $s$ che scorre lungo la parete, si può ugualmente scrivere: $$t (s)\tau (s) = \,cost. \,=\,\bar{t}\,\bar{\tau} \:\:\: \forall s$$ Per valutare il valore specifico di $t (s)\tau (s)$ si calcola il momento risultante dovuto alle $\tau$ da torsione in tutta la sezione rispetto ad un polo qualunque (ad esempio il baricentro della sezione), e lo si pone pari al momento torcente agente sulla sezione: $$M_{t} = \oint t(s) \,\tau(s) r(s) \,ds = \bar{t}\,\bar{\tau}*2A_{m}$$ con $r(s)$ braccio della forza $ t(s) \,\tau(s) \,ds$ rispetto al polo considerato e $ A_{m}$ area all’interno della curva che definisce i piani medi delle pareti. Dunque, punto per punto lungo la sezione si avrà: $$ \tau(s)\,=\,\frac{M_{t}}{2A_{m} \, t(s)}$$ Si noti che la resistenza a torsione della sezione a pareti sottili chiusa dipende da un’area pressoché vuota, vista la definizione di $ A_{m}$; infatti questo tipo di sezione risulta molto vantaggioso in termini di rapporto resistenza/peso. Tramite considerazioni di tipo energetico, si può scrivere la rigidezza torsionale per sezioni sottili chiuse come: $$K_{t}\,=\,\frac{4\,A_{m}^{2}}{\oint \,\frac{1}{t}\,ds}$$ [Si consideri un concio di trave di lunghezza $\Delta z $ alle cui estremità sono applicati due momenti torcenti, entrambi di intensità $M_{t}$ ma in verso opposto. Detto $\Delta\theta $ l’angolo di rotazione relativa tra gli estremi delle estremità del concio, la rigidezza torsionale $K_{t}$ è definita in modo da verificare la seguente espressione: $\Delta \theta \, = \,\Delta z \, \frac{M_{t}}{G\,K_{t}}$ ]
Taglio in sezioni sottili chiuse
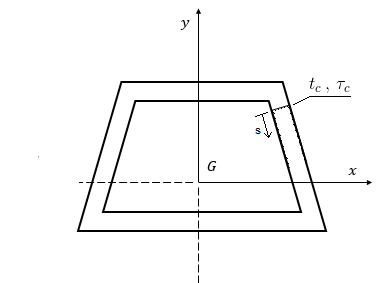
Si prenda una sezione sottile di tipo trapezio, che ha un asse di simmetria, caricata con una forza di taglio $T_{y}$ allineata all’asse di simmetria stesso.
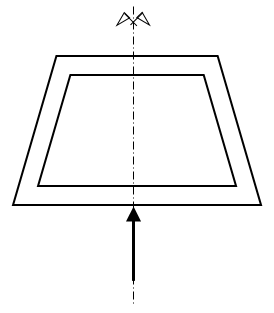
Se c’è simmetria, sia centro di taglio che baricentro appartengono all’asse di simmetria. Non si riesce in questo caso ad isolare un concio di sezione con solo taglio. Nel caso di sezioni simmetriche, facendo due tagli simmetrici, per simmetria anche gli sforzi $\tau$ sono uguali. Dato un certo $\delta \sigma _{z}$, viene equilibrato per metà dalle azioni su un lato e per metà dalle azioni sull’altro. Su sezioni chiuse simmetriche si può dunque applicare Jourawski a patto di isolare il concio di sezione attraverso due tagli simmetrici anziché uno solo.
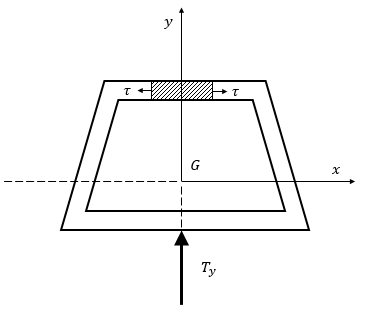
Alternativamente, si può dire che sull’asse di simmetria le $\tau$ sono nulle: isolando una porzione di struttura con due tagli, di cui uno sull’asse di simmetria, il disequilibrio delle $\sigma _{z}$ variabili lungo l’asse viene assorbito interamente dalle $\tau$ presenti sul secondo lato del concio.

Il vero problema si pone se la sezione chiusa non è simmetrica oppure se, pur essendo simmetrica, è caricata da una forza di taglio ortogonale all’asse di simmetria.

In questo caso non si sa più dov’è il centro di taglio. Isolando una porzione di struttura e prendendo il solo disequilibrio di $\sigma _{z}$ non si riesce a trovare la distribuzione di $\tau$, perché non si riesce mai ad isolare un concio con un solo taglio e non c’è nessuna relazione notevole su $\tau$.
Taglio in sezioni sottili chiuse generiche
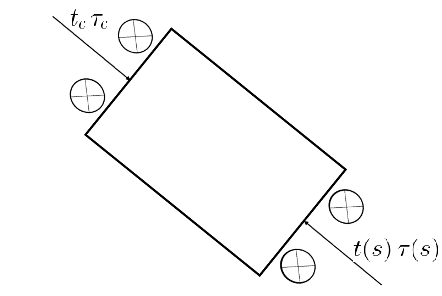
Consideriamo una sezione di riferimento trapezoidale (come la precedente), e definiamo su di essa un’ascissa curvilinea $s$ che scorra lungo tutta la parete sottile. Operiamo un taglio all’interno della sezione e indichiamo con $t _{c}$ lo spessore della sezione e con $\tau _{c}$ le tensioni di taglio presenti in quella specifica sezione.
Operando due tagli all’interno della sezione, è possibile isolarne una porzione.
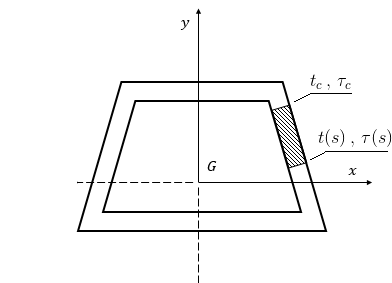
Su questo concio di sezione si consideri il disequilibrio flessionale, che è equilibrato dalle due azioni $t _{c}\tau _{c}$ e $t (s)\tau (s)$.
ATTENZIONE: $\tau_c e \tau(s)$ di figura non possono essere equiversi se utilizzo una comune convenzione per i segni; in particolare dovrebbe risultare $\tau(s)$ uscente e $\tau_c$ entrante
di conseguenza i due contributi dovrebbero avere segno opposto nell'equazione di cui sotto.
Essendo tuttavia $tau_c$ da rilevarsi attraverso la soluzione di un'equazione algebrica, un errato utilizzo della convenzione sui segni dovrebbe essere compensata da un coerentemente errato segno sui risultati.
L’equilibrio alla traslazione fuori piano impone che: $$\tau\left(s \right )t\left(s \right )+ \tau_C t_C =\iint_{A^\star}\frac{d \sigma_z}{dz} d A $$
con $ A^\star$ area compresa dal concio di sezione. Poiché è sempre possibile calcolare l’integrale presente a destra nella precedente formula (in quanto la farfalla flessionale è definita anche per questa sezione), si trova l’espressione di $\tau (s)$ in funzione del parametro $t _{c}\tau _{c}$. Dunque con Jourawsky si ottiene una formulazione di $\tau (s)$ a meno della costante $t _{c}\tau _{c}$.
Assegnare un valore arbitrario a tale quantità equivale, osservando l’analisi tensionale delle sezioni sottili chiuse a torsione, ad imporre un certo valore di momento torcente alla sezione. Si deve dunque scegliere il valore ottimale di $t _{c}\tau _{c}$ che, in questo caso, corrisponda all’avere momento torcente nullo applicato alla sezione (che NON è $t _{c}\tau _{c}=0$).
Si consideri l’energia potenziale elastica associata ad una sezione soggetta sia ad un’azione di taglio sia ad un momento torcente:1) $$U\,=\,\frac{1}{2}\frac{M_{t}^{2}}{G\,K_{t}}\,+ \,\frac{1}{2}\frac{T_{x}^{2}}{G\,A_{m}}\xi$$ con $\xi$ fattore correttivo per il taglio. Essendo il termine legato al momento torcente sempre positivo o al più uguale a zero, quando $ M_{t}=0 $ l’energia potenziale ha un minimo relativo; dunque il valore di $t _{c}\tau _{c}$ che annulla $M_{t}$ è anche punto di minimo di $U$, per il quale si ha:
$$ \frac{\partial U}{\partial t_C \tau_C} = 0 $$
Scrivendo l’energia potenziale elastica come
$$U = \oint \frac{\tau^2(s)}{2G} \,t(s)\, ds$$
è possibile ricavare l’esatto valore di $t _{c}\tau _{c}$ sfruttando le relazioni scritte finora. $$ \frac{\partial U}{\partial \left(\tau_C t_C \right )} = \oint \frac{ +2\left( \tau_C t_C \right) - 2 \left( \int_{0}^{s} \frac{d \sigma_z}{dz} t \;d \cdot \right) }{2G} t\; ds =0 $$ e quindi $$ \tau_C t_C = \frac{ \oint \frac{ \int_{0}^{s} \frac{d \sigma_z}{dz} t \;d \cdot }{G} t\; ds }{\oint \frac{ t }{G} \; ds } $$
Lista dei simboli
| $\mathit{P}$ | carico totale della trave in due elementi |
| $\mathit{l}$ | lunghezza della trave |
| $\mathit{h}$ | altezza della trave |
| $\mathit{b}$ | spessore della trave |
| $M_{f}$ | momento flettente |
| $\sigma_{f}$ | azione assiale dovuta al momento flettente |
| $\tau$ | azione tangenziale |
| $t$ | spessore sezione |
| $G$ | modulo di elasticità a taglio |
| $U$ | energia potenziale elastica |
Autori, note e ringraziamenti
Autori
Andrea Farini, Matteo Fiaschi, mat. 103523, Giovanni Garlaschelli, mat. 104110, Armando Longobardi, mat. 101261.
Tabella di monitoraggio carico orario
Ore-uomo richieste per la compilazione della pagina.
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Andrea Farini | 5 | — | — | — | |
| Matteo Fiaschi | 5 | — | — | — | |
| Giovanni Garlaschelli | 6 | — | — | — | |
| Armando Longobardi | 6 | — | — | — | |
| Vincenzo Marotta | 1 | — | — | — | |
| Revisore 2 | — | — | — | — | |
| Revisore 3 | — | — | — | — | |
| Revisore 4 | — | — | — | — | * |
| Totale |
blabla </hidden>
PATTUME
Taglio in sezioni sottili aperte
Applicazione di Jourawsky su sezioni sottili aperte. Procedura per la determinazione del centro di taglio
Taglio in sezioni sottili chiuse
Applicazione di Jourawsky su sezioni sottili aperte. Procedura per la determinazione del parametro incognito $\tau_c t_c$.
Energia potenziale elastica di un concio di trave in taglio/torsione, $\tau \equiv \tau_{zs}$ con $s$ ascissa curvilinea a scorrere sulla parete sottile a partire dal punto di taglio C.
Definizione $tau(s)$ sui tratti della sezione sottile $$ \tau\left(s \right )t\left(s \right )=\iint_{A^\star}\frac{d \sigma_z}{dz} d A - \tau_C t_C = \int_{0}^{s} \frac{d \sigma_z}{dz} t(\cdot) d \cdot - \tau_C t_C $$
Energia associata alla combinazione taglio / momento torcente indotto dal carico traverso se applicato con braccio $d$ rispetto al centro di taglio
$$ U = \oint \frac{\tau^2(s)}{2G} t(s) ds=\oint \frac{\left( \int_{0}^{s} \frac{d \sigma_z}{dz} t(\cdot) d \cdot - \tau_C t_C \right)^2}{2G} t(s) ds =\frac{1}{2}T_y v_C + \underbrace{ \frac{1}{2} \underbrace{T_y d}_{M_t} \theta}_{\leq 0} $$ ove $v_C$ è lo spostamento in direzione y del centro di taglio
Essendo l'energia relativa al momento torcente $\leq 0$, il caso a $d$ nullo è un minimo dell'energia potenziale elastica.
$$ \frac{\partial U}{\partial t_C \tau_C} = 0 $$
$$ \frac{\partial U}{\partial \left(\tau_C t_C \right )} = \oint \frac{ +2\left( \tau_C t_C \right) - 2 \left( \int_{0}^{s} \frac{d \sigma_z}{dz} t \;d \cdot \right) }{2G} t\; ds =0 $$ e quindi $$ \tau_C t_C = \frac{ \oint \frac{ \int_{0}^{s} \frac{d \sigma_z}{dz} t \;d \cdot }{G} t\; ds }{\oint \frac{ t }{G} \; ds } $$