Indice
Azione interna in travi spaziali: stato tensionale e deformativo
Con particolare riferimento a profilati in parete sottile.
Richiami di teoria dell'elasticità
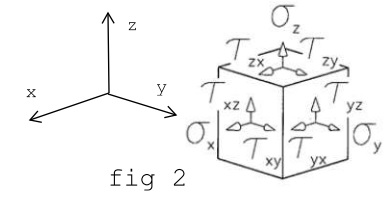
Stato tensionale
Stato deformativo

Legame costitutivo
Legame tra componenti di tensione e componenti di deformazione per un materiale elastico lineare isotropo
$$ \def\X{\frac{E\left(1-\nu\right)}{\left(1-2\nu\right)\left(1+\nu\right)}} \def\Y{\frac{E\nu }{\left(1-2\nu\right)\left(1+\nu\right)}} \begin{bmatrix} \sigma_{x}\\ \sigma_{y}\\ \sigma_{z}\\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{bmatrix} = \begin{bmatrix} \X&\Y&\Y&0&0&0 \\ \Y&\X&\Y&0&0&0 \\ \Y&\Y&\X&0&0&0 \\ 0 &0 &0 &G&0&0 \\ 0 &0 &0 &0&G&0 \\ 0 &0 &0 &0&0&G \end{bmatrix} \begin{bmatrix} \epsilon_{x}\\ \epsilon_{y}\\ \epsilon_{z}\\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{bmatrix} $$
$$ \def\X{\frac{1} {E}} \def\Y{\frac{-\nu}{E}} \def\Z{\frac{1} {G}} \begin{bmatrix} \epsilon_{x}\\ \epsilon_{y}\\ \epsilon_{z}\\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{bmatrix} = \begin{bmatrix} \X&\Y&\Y&0&0&0 \\ \Y&\X&\Y&0&0&0 \\ \Y&\Y&\X&0&0&0 \\ 0 &0 &0 &\Z&0&0 \\ 0 &0 &0 &0&\Z&0 \\ 0 &0 &0 &0&0&\Z \end{bmatrix} \begin{bmatrix} \sigma_{x}\\ \sigma_{y}\\ \sigma_{z}\\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{bmatrix} $$
Si noti che:
- E rappresenta il modulo di Young,
- $\nu$ rappresenta il coefficiente di Poisson (per i materiali di nostro interesse, principalmente metallici, vale circa 0,3)
- G rappresenta il modulo di taglio, legato a E e $\nu$ dalla relazione:
$$ G=\frac{E}{2\left ( 1+\nu \right )} $$
Sforzo normale e momento flettente (puro)
Si considera uno stato tensionale uniassiale $\sigma_z = E \epsilon_z$.
Taglio
Applicazione della formula di Jourawski a sezioni in parete sottile aperta e chiusa.
Taglio in sezioni sottili aperte
Applicazione di Jourawsky su sezioni sottili aperte. Procedura per la determinazione del centro di taglio
Taglio in sezioni sottili chiuse
Applicazione di Jourawsky su sezioni sottili aperte. Procedura per la determinazione del parametro incognito $\tau_c t_c$.
Energia potenziale elastica di un concio di trave in taglio/torsione, $\tau \equiv \tau_{zs}$ con $s$ ascissa curvilinea a scorrere sulla parete sottile a partire dal punto di taglio C.
Definizione $\tau(s)$ sui tratti della sezione in parete sottile $$ \tau\left(s \right )t\left(s \right )=\iint_{A^\star}\frac{d \sigma_z}{dz} d A - \tau_C t_C = \int_{0}^{s} \frac{d \sigma_z}{dz} t(\cdot) d \cdot - \tau_C t_C $$
Suppongo qui $\sigma_z$ uniforme lungo lo spessore (stato di taglio membranale).
Energia associata alla combinazione taglio / momento torcente indotto dal carico traverso se applicato con braccio $d$ rispetto al centro di taglio
$$ U = \oint \frac{\tau^2(s)}{2G} t(s) ds=\oint \frac{\left( \int_{0}^{s} \frac{d \sigma_z}{dz} t(\cdot) d \cdot - \tau_C t_C \right)^2}{2G} t(s) ds =\frac{1}{2}T_y v_C + \underbrace{ \frac{1}{2} \underbrace{T_y d}_{M_t} \theta}_{\geq 0} $$ ove $v_C$ è lo spostamento in direzione y del centro di taglio
Essendo l'energia relativa al momento torcente $\geq 0$, il caso a $d$ nullo è un minimo dell'energia potenziale elastica.
$$ \frac{\partial U}{\partial t_C \tau_C} = 0 $$
$$ \frac{\partial U}{\partial \left(\tau_C t_C \right )} = \oint \frac{ +2\left( \tau_C t_C \right) - 2 \left( \int_{0}^{s} \frac{d \sigma_z}{dz} t(\cdot) \;d \cdot \right) }{2G} t\; ds =0 $$ e quindi $$ \tau_C t_C = \frac{ \oint \frac{ \int_{0}^{s} \frac{d \sigma_z}{dz} t \;d \cdot }{G} t\; ds }{\oint \frac{ t }{G} \; ds } $$
Torsione
PATTUME
Lucidi della lezione
Lucidi e appunti spicci
Materiale di riferimento/approfondimento per sezioni in parete sottile chiusa e aperta a torsione
C. Felippa, Torsion Of Open Thin Wall (OTW) Sections C. Felippa, Torsion Of Closed Thin Wall (CTW) Sections