Indice
ARGOMENTI DELLA LEZIONE
In questa lezione si sono trattati tre diversi argomenti:
- Comandi vari di maxima;
- Introduzione al FEM:Finite Element Method;
- Introduzione al software Marc Mentat.
COMANDI VARI DI MAXIMA
Il file utilizzato nel laboratorio è il seguente: comandi sparsi maxima
Descrizione della funzione di alcuni comandi utili di Maxima di cui non è stata fatta menzione durante le lezioni precedenti al laboratorio odierno. Informazioni ed esempi ulteriori si possono trovare nella guida di Maxima accessibile dal menu aiuto, oppure digitando, rispettivamente, le istruzioni “describe (comando)” ed “example (comando)” direttamente nel testo del programma.
ratsubst (a, b, expr)
Sostituisce gli elementi “b” dell’espressione “expr” con l’elemento “a” e restituisce l’espressione risultante.
fullratsubst (a, b, expr)
La funzione “fullratsubst (a, b, expr)” ha le stesse caratteristiche della precedente, ma si reitera fino a che il risultato non varia più a seguito di un'ulteriore sostituzione. Utile quando l’espressione risultante e quella da modificare hanno una o più variabili in comune.
assume (pred_1, …, pred_n)
Attribuisce delle specifiche condizioni a uno o più elementi e restituisce una lista contenente le assunzioni assegnate. I predicati “pred_1, …, pred_n” assegnati possono essere solamente espressioni con gli operatori relazionali “>” , “<” ed “=”.
forget (pred_1, …, pred_n)
Rimuove le assunzioni stabilite tramite il comando assume.
makelist (expr, i, i_0, i_max, step)
Restituisce una lista di elementi ottenuti dall’espressione “expr” sostituendo la variabile “i” con valori che vanno da “i0” a “imax”; “step” indica il passo da considerare tra due elementi dell’intervallo “[i_0, …, i_max]”, può essere omesso.
plot2d ([plot_1, …, plot_n], x_range, legend)
Visualizza in una finestra secondaria il grafico di uno o più “plot” forniti in una lista, che possono essere espressioni, funzioni o liste. Quando si vogliono visualizzare più grafici, questi devono dipendere tutti da una variabile definita in “x_range” la cui sintassi è “[var, min, max]” dove si esplica la variabile considerata in “var”, il suo valore minimo “min” e massimo “max”. I plot possono anche essere definiti nella forma “[discrete, [x1, …, xn], [y1, …, yn]]”. “discrete” indica l’uso della forma discreta, che plotta un set di punti con le rispettive coordinate. Le liste successive devono avere la stessa lunghezza e sono interpretate rispettivamente come le coordinata “x” e “y” dei punti da plottare. L’istruzione “legend” è facoltativa, specifica le etichette dei grafici visualizzati. La sintassi del comando è “[legend, name_1, …, name_n]”. Se viene omesso, le curve sono chiamate con il nome del plot corrispondente.
wxplot2d ([plot_1, …, plot_n], x_range, legend)
Per visualizzare il grafico all’interno della finestra di Maxima basta usare “wxplot2d”.
trigsimp (expr)
Semplifica le identità trigonometriche note nell’espressione “expr”.
trigexpand (expr)
Espande le funzioni trigonometriche di somme di angoli all’interno di “expr”. Il comando si ripete una volta, per implementarlo continuamente fino a che il risultato non cambia più (ovvero non ci sono più funzioni da sostituire), bisogna mettere una virgola dopo “trigexpand (expr)” e poi digitare “trigexpandtimes=true”.
solve (expr, x)
Risolve l’equazione algebrica “expr” rispetto alla variabile “x” e restituisce la lista delle soluzioni. Se la soluzione dell’equazione non è univoca, l’istruzione “globalsolve = true” (che assegna alla variabile “x” il valore della soluzione appena ottenuta) non può essere usata, il valore di “x” va attribuito tramite un’assegnazione successiva. Se l’equazione è fornita senza il segno “=”, Maxima assume implicitamente “expr=0”.
comandi base per i numeri complessi
In Maxima un numero complesso è composto dalla somma della parte reale e della parte immaginaria moltiplicata per l’unità immaginaria “%i”. I comandi “realpart (expr)” e “imagpart (expr)” forniscono rispettivamente la parte reale e la parte immaginaria di “expr”. La funzione “exponentialize (expr)” converte un’espressione trigonometrica nella sua forma esponenziale complessa. Al contrario, “demoivre (expr)” compie il passaggio inverso, cioè gli esponenziali complessi della funzione “expr” vengono convertiti nelle equivalenti funzioni trigonometriche.
quad_qag (f(x), x, a, b, key)
Per un computer è impossibile calcolare un integrale analiticamente, perciò bisogna approssimarlo. L’integrazione numerica, o quadratura numerica, consiste in una serie di metodi che stimano il valore di un integrale definito, senza dover calcolare la primitiva della funzione integranda. In Maxima questa operazione è implementata dal comando “quad_qag” che integra la funzione “f(x)” secondo la variabile dipendente “x”, tra gli estremi “a” (inferiore) e “b” (superiore). “key” è un numero tra 1 e 6, indica il metodo di quadratura da adottare (solitamente si utilizza il metodo 1, i metodi di ordine maggiore sono usati per integrandi fortemente oscillanti). “quad_qag” restituisce una lista di 4 elementi, che sono rispettivamente:
- risultato dell’integrazione numerica;
- errore assoluto stimato;
- numero di valutazioni della funzione;
- codice errore (0 indica che non si riscontrano errori).
zeromatrix (m, n)
Crea una matrice di m righe ed n colonne, composta solo da zeri. È possibile assegnare un valore arbitrario ad un elemento specifico della matrice, specificando prima il nome della matrice in questione, i numeri rispettivamente di riga e colonna dell’elemento desiderato tra parentesi quadre, il simbolo di assegnazione “:” e il valore da assegnare.
transpose (A)
Restituisce la trasposta della matrice “A”, cioè una seconda matrice “A’” tale per cui “A [i,j] = transpose (A) [j,i]”. Se “A” è una matrice triangolare superiore, digitando “A – transpose (A)” si crea una matrice antisimmetrica, ovvero una matrice la cui trasposta è pari alla sua opposta.
matrix ([r_1], …, [r_n])
Costruisce una matrice rettangolare le cui righe sono composte dagli elementi delle liste “[r_1], …, [r_n]”. Tutte le liste devono avere lo stesso numero di elementi.
genmatrix (a, m, n)
Genera una matrice di “m” righe ed “n” colonne in base alle istruzioni fornite in “a”. “a” può essere definito da un’espressione “lambda” costruita come segue: “lambda ( [i,j], f(i,j) )” dove “f(i,j)” è una generica funzione di “i” (indice riga) e “j” (indice colonna) che fornisce come risultato il valore dell’elemento in posizione “i,j”.
coefmatrix ([eq_1, …, eq_n], [x_1, …, x_n])
Restituisce una matrice con i coefficienti delle variabili “x_1, …, x_n” del sistema di equazioni lineari “eq_1, …, eq_n”. Le equazioni possono essere dichiarate direttamente all’interno di “coefmatrix”, in alternativa è sufficiente richiamare equazioni già definite precedentemente. Per visualizzare anche la colonna dei termini noti bisogna usare il comando “augcoefmatrix”. Le equazioni “eq_1, …, eq_n” vengono considerate automaticamente in forma implicita.
prodotto tra matrici
Il simbolo dell’operatore del prodotto riga per colonna tra due matrici è “.“.
calcolo del determinante di una matrice
Il comando “determinant (A)” calcola il determinante della matrice “A”.
INTRODUZIONE AL FEM: FINITE ELEMENT METHOD
Il metodo FEM è un metodo numerico, sviluppato per risolvere il problema del calcolo degli sforzi nelle strutture. È indicato per risolvere problemi complessi ed avere informazioni sullo stato tensionale dei componenti o delle strutture.
PRIMO PASSO: SUDDIVIDERE LA STRUTTURA IN ELEMENTI
L’intera geometria è suddivisa in porzioni dette elementi, a formare un reticolo che prende il nome “mesh”. Gli elementi servono a descrivere il campo degli spostamenti in maniera semplice, di solito attraverso una rappresentazione polinomiale. I nodi (non necessariamente i vertici), e non i lati, sono i punti di collegamento tra gli elementi.
GLI ELEMENTI E IL CAMPO DEGLI SPOSTAMENTI
Gli elementi o celle si dividono in 2D e 3D. In base al tipo di elemento di utilizzato il numero di G.D.L. può variare da 2 a 6-7.
Tra quelli 2D i più utilizzati sono quelli triangolari, ma ne esistono anche quadrati o segmenti (conci di trave). Le celle esaedriche o i prismi a base triangolare sono inevece diffuse nel 3D.
L’unione di tutti gli elementi dà un’approssimazione sfaccettatata del dominio elastico.
Il primo errore del metodo è legato alla dimensione degli elementi: per non avere errore di discretizzazione sono necessari elementi di dimensione tendente a zero, non utilizzabili perchè comporterebbero infiniti gradi di libertà, perciò gli elementi avranno dimensioni finite, da cui il nome FEM.
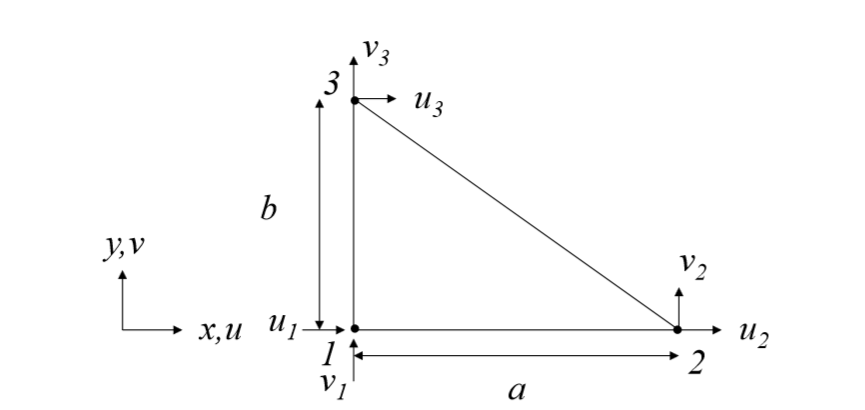
Ad ogni nodo si associano delle incognite per gli spostamenti nelle direzioni cartesiane e per le rotazioni. Per descrivere gli spostamenti di un punto interno al triangolo si definiscono le funzioni di forma per ogni nodo.
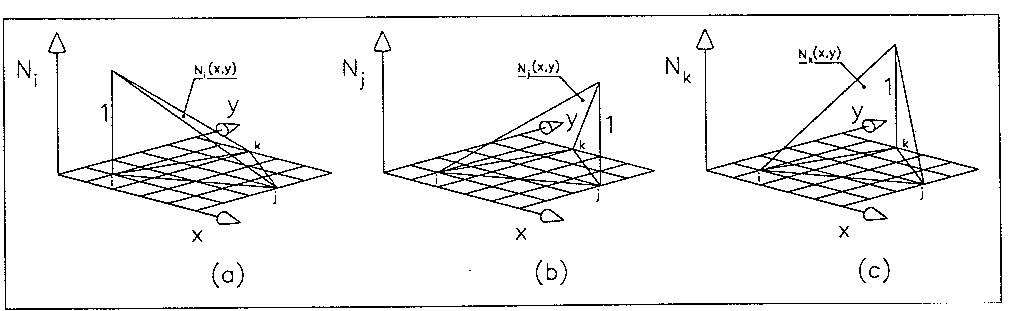
Quest’ultime possono essere:
- Lineari
- Quadratiche
- Cubiche
- Bilineari
Sono funzioni che valgono 1 sul nodo associato e 0 sugli altri. La funzione di forma del nodo “i” è “Ni”. Essa è una porzione triangolare del piano. Lo spostamento di un punto interno del triangolo è la media pesata degli spostamenti dei nodi. I pesi saranno proprio le funzioni di forma.
$U(x,y)= N_{i}(x,y)\times U_{i}+N_{j}(x,y)\times U_{j}+N_{k}(x,y)\times U_{k}$
Tale formula vale anche per punti esterni, ma in genere non si ha interesse nell’ utilizzarla in tale modo. Dopo aver legato il campo di spostamenti all’interno di ogni elemento ai valori degli spostamenti assunti dai nodi si procede alla soluzione del problema elastico impostato in modo da ottenere il valore degli spostamenti nodali (spostamenti e rotazioni). Essendo questi le nostre incognite, il metodo si dice anche metodo agli spostamenti. Non è possibile però definire qualunque spostamento. Se infatti si usano funzioni di forma lineari, gli elementi non potranno curvarsi. A questo punto risulta evidente il secondo errore del metodo: con le definizioni degli spostamenti si aumenta la rigidezza della struttura, ovvero data la struttura e i carichi troverò spostamenti inferiori rispetto a quelli reali e, allo stesso modo, imponendo gli spostamenti otterrò rigidezze maggiori di quelle effettive. Queste approssimazioni sono accettabili per avere un metodo che ci consente di fare i calcoli e risolvere il problema iniziale. La continuità delle soluzioni è garantita perché valgono gli stessi spostamenti sui nodi in comune tra più lati, questo significa che per modellare una cricca sono necessari due nodi sovrapposti, altrimenti sarà impossibile per gli elementi allontanarsi. L’elemento rappresenta anche un’iperstaticità che definisce la reazione elastica del materiale quando subisce una deformazione diversa da quella di corpo rigido.
Nel nostro esempio di una lastra piana forata con sforzo di trazione uniforme il corpo è piano con deformata piana. Posso quindi eliminare l’incognita in direzione “z”. Per semplificare ancora il problema e occupare meno memoria RAM, essendo struttura e carichi simmetrici possiamo occuparci di un quarto di piastra e ottenere una soluzione più rapida.
Riferimenti: The Finite Element Method da Boresi Schmidt, 5a edizione.
INTRODUZIONE A MARC MENTAT
È un software nato negli anni ’70, il codice è indicato per il calcolo di strutture non lineari. Questo software è composto da due parti, l’interfaccia grafica e il solutore; rispettivamente Mentat e Marc. Si noti come sia possibile eseguire dal computer in uso l’interfaccia grafica e mandare i file *.txt, contenente i dati e le matrici per il calcolo, al solutore che può essere un server collegato in rete e molto più potente di quello in uso.
LANCIARE MARC MENTAT
Riga di comando per lanciare il software:
mentat2013.1 -ogl -glflush
NOTA BENE
Prima di introdurre i comandi basilari del software si faccia notare che:
- Tutte le scritte in VERDE indicano un MENU;
- Tutte le scritte in GIALLO indicano un COMANDO.
Ogni volta che si fornisce un input (che sia scrivere parole o numeri) si deve sempre premere “invio” per poterlo inserire nel software.
Nel caso in cui il software sembri bloccato, controllare che non ci siano altre finestre dello stesso che richiedano un input.
Si ha a disposizione un solo “undo” (annulla), infatti al primo undo verrà annullata l’operazione precedente; ma se premuto una seconda volta verrà annullato l’annulla precedente facendo tornare la modifica precedentemente annullata. Pertanto si consiglia di salvare varie versioni del file
GUIDA ALLE ESTENSIONI DEI FILE
Il software utilizza le seguenti estensioni:
- *.mfd, *.mud sono le estensioni con cui viene salvato il modello;
- *.dat è il file che viene dato come input al solutore (Marc);
- *.t16, *t19 sono i file in cui vengono salvati l’output del solutore;
- *.log, *.out contengono una specie di diario su cui vengono riportate tutte le azioni e gli errori del solutore.
APRIRE E SALVARE UN FILE
Per aprire un file
FILES → OPEN
NOTA BENE: una volta aperto il file apparirà una crocetta al centro dello spazio di visualizzazione del modello, premere “fill” per regolare automaticamente lo zoom e visualizzare il modello importato.
Per salvare un file con nome
FILES → SAVE AS
Per salvare un file
FILES → SAVE
MUOVERE IL MODELLO NELLO SPAZIO
DYNAMIC MODEL
Se il “led” relativo è acceso il dynamic model è “on”, altrimenti se il led è spento esso è su “off”.
- Se il led è acceso con il mouse è possibile ruotare e spostare la vista;
- Se il led è spento con il mouse è possibile selezionare gli oggetti.
COMANDI MOUSE
TASTO DESTRO: Tenendo cliccato il tasto si può trascinare il mouse verso l’esterno o l’interno per aumentare o diminuire lo zoom;
TASTO CENTRALE: Tenendolo premuto si può ruotare il modello;
TASTO SINISTRO: Tenendolo premuto si può trascinare il modello.
COMANDI VISTA
FILL: Regola lo zoom in modo da vedere l’intero modello a schermo.
RESET VIEW: Si porta la vista con piano z negativo disposto perpendicolarmente rispetto allo schermo.
RZ+: Ruota di 10° in senso positivo rispetto a Z il modello. RZ-: Ruota di 10° in senso negativo rispetto a Z il modello. Quanto visto per RZ+ e RZ- vale anche per RY+, RY-, RX+, RX-.
ZOOM BOX: Tenere cliccato il tasto sinistro del mouse, si disegni il rettangolo che contenga la zona del modello che si vuole zoomare. Una volta rilasciato il mouse la zona selezionata occuperà tutto lo schermo.
CAMBIARE LO SFONDO IN BIANCO
Per cambiare il colore dello sfondo da nero a bianco:
UTILS → POSTSCRIPT → SETTINGS → PREDIFINED COLORMAPS → 2
Per portare lo schema dei tasti in scala di grigi:
CONFIGURATION → DEVICE → MENU COLORS → COLOR TABLE→ GRAY
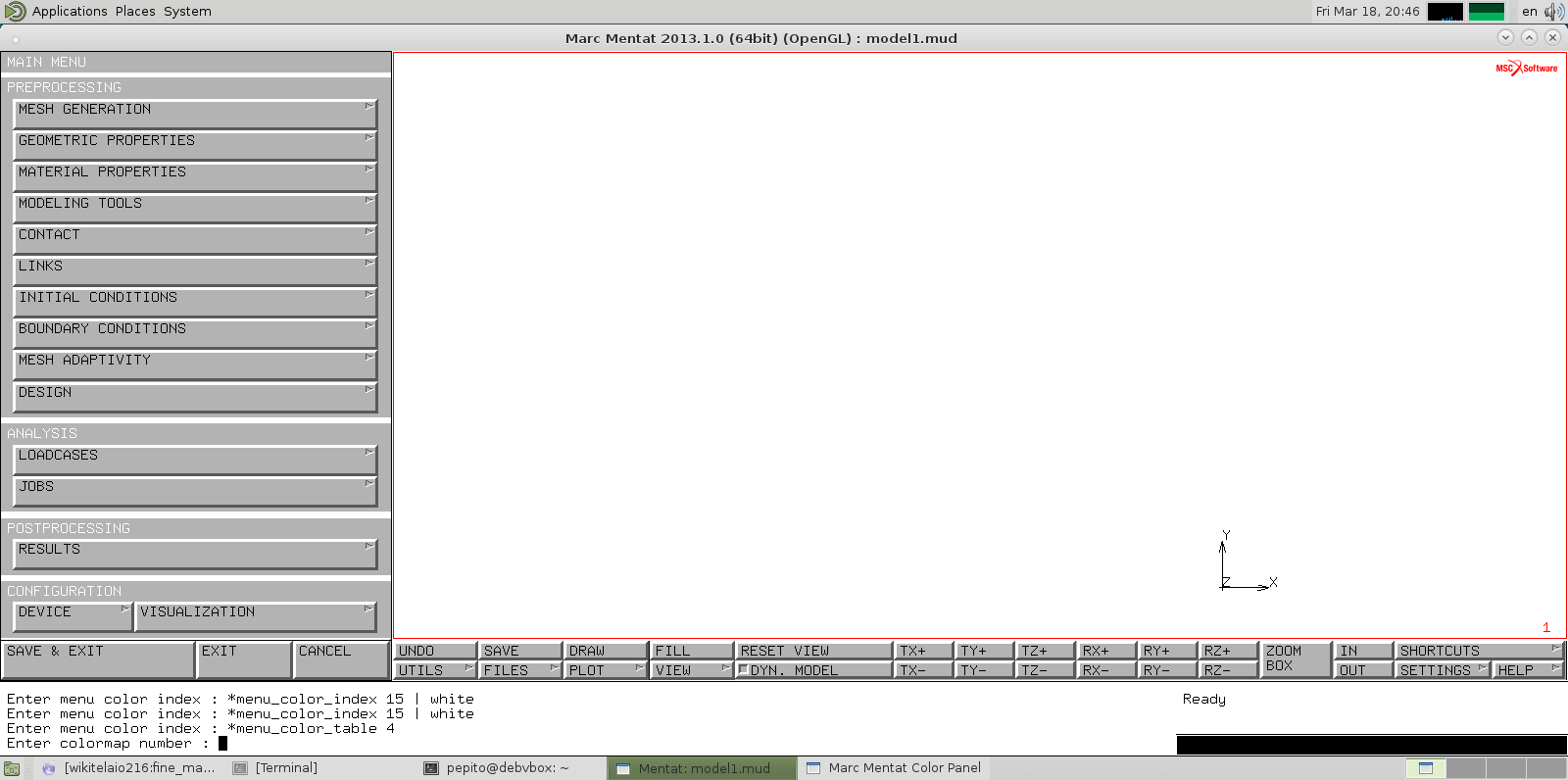
NAVIGAZIONE NEI MENU
In ogni menù si hanno 2 comandi:
RETURN: Torna al menu precedente (in alternativa si può cliccare il tasto destro del mouse).
MAIN: Torna al menu principale.
MIGLIORARE LA VISUALIZZAZIONE DELLE CURVE
Per migliorare la visualizzazione delle curve ed eliminare la “sfaccettatura” delle stesse.
PLOT → CURVES → SETTINGS → PREDIFINED SETTINGS → HIGH → REGEN
NASCONDERE ELEMENTI
Se si vogliono nascondere le curve del modello o i nodi, ect.
PLOT → CLICCARE E SPEGNERE IL LED DELL'ELEMENTO DA NASCONDERE → REGEN
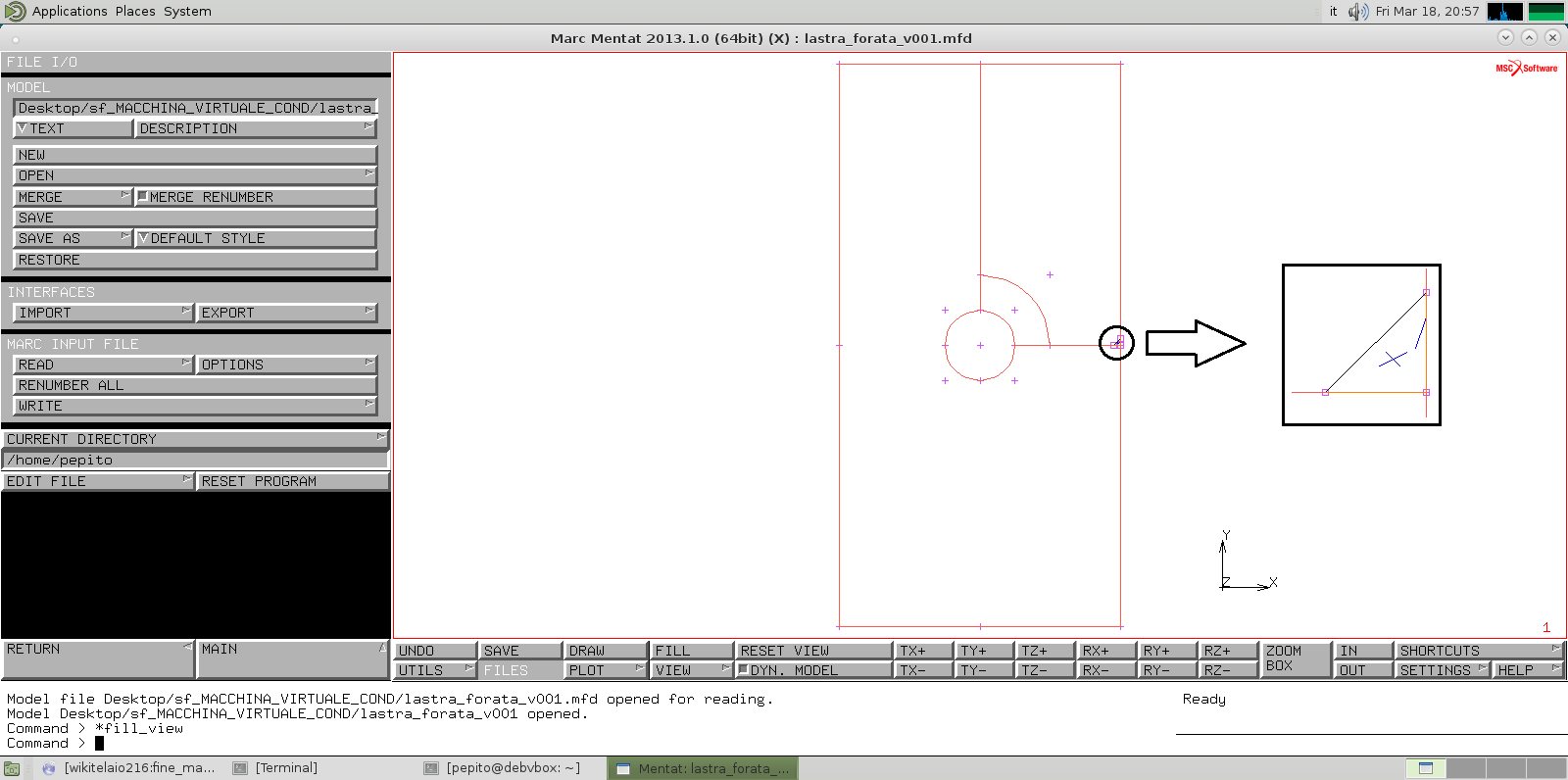
ESEMPIO DELLA PIASTRA FORATA
Si consideri il modello d’esempio presente in questa pagina lastra_forata_v000.mfd . Esso viene fornito con la mesh già eseguita, si vogliono cancellare tutti gli elementi finiti triangolari tranne quello in basso a destra.
VISUALIZZAZIONE LINEE DEL MODELLO
Nel modello vengono utilizzati diversi colori:
ROSA: Indica i nodi.
NERO: indica le linee che compongono gli elementi finiti (se si avesse lo sfondo nero allora queste linee sarebbero bianche).
ARANCIONE: indica le linee che compongono il modello.
ELIMINAZIONE ELEMENTI
Per eliminare gli elementi non necessari:
MESH GENERATION → ELEMENTS → REMOVE → SELEZIONARE GLI ELEMENTI → END LIST
NOTA BENE: Si controlli che il led del dynamic mode sia spento per poter selezionare gli oggetti. Invece che premere “end list” è possibile premere il tasto destro del mouse o digitare “#”.
SELEZIONE DEGLI ELEMENTI: Gli elementi sono selezionabili tenendo premuto il tasto sinistro del mouse e facendoli stare all’interno, gli elementi che non saranno completamente all’interno di tale rettangolo non saranno selezionati.
DESELEZIONE: Per deselezionare gli ultimi elementi selezionati cliccare il tasto centrale del mouse.
ELIMINAZIONE DEI NODI INUTILIZZATI
Una volta eliminati gli elementi rimangono i nodi inutilizzati, quindi per eliminarli:
MESH GENERATION → SWEEP → REMOVE UNUSED → NODES
COLLASSO DEI NODI AL DI SOTTO DI UNA CERTA DISTANZA
Per eliminare i nodi che si trovano al di sotto di una certa distanza definita nel menu:
UTILS → DISTANCE → SELEZIONARE I DUE NODI
ASSEGNARE LE PROPRIETA’ PER LA SIMULAZIONE
Nel caso in esame dato che la piastra è sottile e il caricamento è uniforme si suppone che la deformazione dell’elemento finito sia piana, per assegnare questa condizione all’elemento:
GEOMETRIC PROPRIETES → NEW → STRUCTURAL →PLANAR → PLANE STRESS
ASSEGNARE LO SPESSORE ALLA PIASTRA
Per assegnare lo spessore alla piastra:
GEOMETRIC PROPRIETES → THICKNESS → DIGITARE IL VALORE DELLO SPESSORE → SELEZIONARE GLI ELEMENTI
IDENTIFICARE LE PROPRIETA’ ASSEGNATE
Per identificare graficamente le diverse proprietà assegnate, visualizzate ognuna con un colore diverso:
GEOMETRIC PROPROPERTIES → ID. GEOMETRIES
MODELLO DI FINE ESERCITAZIONE
Il modello a cui si è giunti alla fine dell'esercitazione, cioè con tutti i nodi e gli elementi eliminati tranne quello in basso a desta è scaricabile da lastra_forata_v001.mfd Il risultato finale sarà il seguente:
Autori, note e ringraziamenti
- Agazio Gianluca Lucifero mat. 101168
- Federico Lodigiani mat. 101938
- Alessandro Mattei mat. 101383
Tabella di monitoraggio carico orario
Ore-uomo richieste per la compilazione della pagina.
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Lucifero | 6 | — | — | — | 6 |
| Lodigiani | 6 | — | — | — | 6 |
| Mattei | 6 | — | — | — | 6 |
| Andrea Gombia | — | 2 | — | — | — |
| Revisore 2 | — | — | — | — | — |
| Revisore 3 | — | — | — | — | — |
| Revisore 4 | — | — | — | — | — |
| Totale | 18 | — | — | — | 18 |
La sezione relativa ai revisori è da compilarsi a cura del curatore. </hidden>
PATTUME
Maxima
carrellata varie istruzioni utili. comandi sparsi maxima
Metodo degli Elementi finiti
Modello di riferimento: lastra_forata_v000.mfd
Riga di comando per lanciare Mentat
mentat2013.1 -ogl -glflush
Riferimenti: The Finite Element Method da Boresi Schmidt, 5a edizione.