Indice
Lezione 3
Funzione di forma
Considero un elemento triangolare a tre nodi.
Ai tre nodi $\mathbf{i}$, $\mathbf{j}$ e $\mathbf{k}$ è possibile associare tre funzioni di forma.
- $N_{i} (x,y)$
- $N_{j} (x,y)$
- $N_{k} (x,y)$
L’andamento delle funzioni di forma è per scelta, lineare e ad ognuna di essa è associato un grado di libertà. Se ci fosse un grado di libertà “pressione idrostatica al centro dell’elemento” avrei anche una funzione di forma associata.
La funzione di forma è una funzione che ha questa caratteristica:
- associata al nodo $\mathbf{i}$ ha valore $\mathbf{1}$ sul nodo $\mathbf{i}$ e valore $\mathbf{0}$ sui nodi $\mathbf{j}$ e $\mathbf{k}$.
- associata al nodo $\mathbf{j}$ ha valore $\mathbf{1}$ sul nodo $\mathbf{j}$ e valore $\mathbf{0}$ sui nodi $\mathbf{i}$ e $\mathbf{k}$.
- associata al nodo $\mathbf{k}$ ha valore $\mathbf{1}$ sul nodo $\mathbf{k}$ e valore $\mathbf{0}$ sui nodi $\mathbf{i}$ e $\mathbf{j}$.
| nodo $i$ | nodo $j$ | nodo $k$ | |
|---|---|---|---|
| $N_{i} (x,y)$ | 1 | 0 | 0 |
| $N_{j} (x,y)$ | 0 | 1 | 0 |
| $N_{k} (x,y)$ | 0 | 0 | 1 |
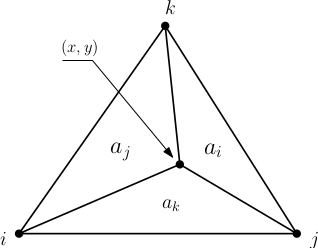
Considerando la seguente figura è possibile definire:
- $N_{i}(x,y)=\frac{a_{i}}{a}$
- $N_{j}(x,y)=\frac{a_{j}}{a}$
- $N_{k}(x,y)=\frac{a_{k}}{a}$
dove $a$ è l'area totale dell'elemento triangolare, mentre $a_{i}$, $a_{j}$, $a_{k}$ sono le aree dei triangoli opposti ai nodi $i$, $j$, $k$.
Una volta definite queste tre funzioni, posso scrivere gli spostamenti in direzione $x$ entro l’elemento come:
$$ u\left(x,y\right)=N_i\left(x,y\right)u_i+N_j\left(x,y\right)u_j+N_k\left(x,y\right)u_k $$
Lo spostamento in direzione $x$ all’interno del triangolo è definito come combinazione, con pesi $u_{i}$ , $u_{j} $ , $u_{k} $ , dei valori che le tre funzioni di forma hanno in quel punto.
Stesso dicasi per $v(x,y)$:
$$ v\left(x,y\right)=N_i\left(x,y\right)v_i+N_j\left(x,y\right)v_j+N_k\left(x,y\right)v_k $$
Quindi, un’alternativa a definire una forma lineare del campo degli spostamenti entro l’elemento è definire tre funzioni di forma lineari, una per ogni grado di libertà (la cui combinazione sarà implicitamente un campo lineare), e combinando quelle funzioni di forma (quei valori delle incognite legati ai gradi di libertà) trovo tutto il campo degli spostamenti entro l’elemento.
In definitiva posso costruire elementi semplicemente definendo grado di libertà e relative funzioni di forma.
Torniamo alla definizione di spostamento come combinazione lineare di $\alpha_{1} $, $\alpha_{2} $,…, $\alpha_{6} $.
$$ u(x,y)=\alpha_{1}+\alpha_{2}x+\alpha_{3}y $$ $$ v(x,y)=\alpha_{4}+\alpha_{5}x+\alpha_{6}y $$
E' noto che dal campo degli spostamenti posso ricavare le deformazioni per differenziazione come segue:
$$ \varepsilon_{x}=\frac{\partial u}{\partial x}=\alpha_{2} $$ $$ \varepsilon_{y}=\frac{\partial v}{\partial y}=\alpha_{6} $$ $$ \gamma_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}=\alpha_{3}+\alpha_{5} $$
Risulta che ad esempio, quando passo dagli spostamenti alle deformazioni, le quote $\alpha_{1} $ e $\alpha_{4} $ scompaiono, ossia $\alpha_{1} $ e $\alpha_{4} $ sono delle quote di spostamento che non generano deformazione. $\alpha_{1} $ possiamo caratterizzarla come una traslazione rigida in direzione $x$, $\alpha_{4} $ è una traslazione rigida in direzione $y$, e quindi possiamo misurare i due moti di corpo rigido. I moti di corpo rigido, per definizione, sono moti in cui l’elemento non si deforma. Quindi per questo stato di deformazione sono nulli. Pertanto si può dire che le deformazioni sono nulle per:
$$ \alpha_{1}=\lambda_{1} \qquad \forall\lambda $$ $$ \alpha_{4}=\lambda_{2} \qquad \forall\lambda $$
Ma si hanno deformazioni nulle anche nel caso in cui $\alpha_{3} $ e $\alpha_{5} $ sono uguali e opposte:
$$ \alpha_{3}=\lambda_{3} $$ $$ \alpha_{5}=-\lambda_{3} $$ $$ \Rightarrow\alpha_{3}=-\alpha_{5} $$
In forma parametrica ho definito quelle tre forme di spostamento che danno deformazioni nulle.
Analizziamo il significato geometrico di $\alpha_{3} $ e $\alpha_{5} $.
Possiamo vedere come $\alpha_{3} $ e $\alpha_{5} $ sono legati ad una deformazione di tipo di rotazione.
Considero il piano $xy$.
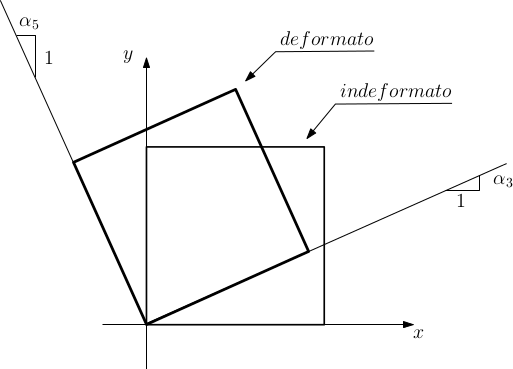
Ho un elemento che inizialmente nasce come un quadrato. Supponiamo di dare un moto che sia legato puramente ai coefficienti $\alpha_{3} $ e $\alpha_{5} $. La deformazione che ottengo è una deformazione tipo “rombo”.
Il quadrato è l’indeformata. Il rombo è la deformata.
Consideriamo il lato del quadrato giacente sull’asse $x$ in configurazione indeformata.
Notiamo che:
- il punto ad $x=0$, in configurazione deformata, è rimasto fermo in questo esempio di pura deformazione a taglio;
- gli altri punti del lato si spostano in direzione verticale sempre di più (per $x$ crescenti).
In particolare la funzione spostamento verticale $v(x,y)$ cresce con legge lineare.
La pendenza possiamo vederla legata a $\frac{\partial v}{\partial x}$. Cioè la variazione di spostamento in direzione $y$, man mano mi muovo in $x$, dà luogo a questa forma del lato deformato del cubetto (quello del rombo) ed è legata a $\frac{\partial v}{\partial x}$, che nel caso specifico è uguale ad $\alpha_{5} $.
Se $v$ fosse uguale a zero per ognuno di questi punti, $v$ sarebbe una costante in $x$ e $\frac{\partial v}{\partial x}$ sarebbe uguale a zero e questo lato rimarrebbe sulla configurazione indeformata.
Consideriamo adesso il lato del quadrato giacente sull’asse $y$ in configurazione indeformata.
In questo caso la configurazione deformata è legata allo spostamento in direzione $x$, via via crescente in $y$, dei nodi che, in configurazione indeformata, si trovavano sull’asse $y$.
In particolare:
- il nodo ad $y=0$ non si sposta in direzione $x$;
- il nodo in corrispondenza dell’altro estremo del lato considerato si sposta di una data quantità;
- tutti i nodi si spostano con legge lineare.
Possiamo quindi vedere come pendenza di questo lato sulla deformata la derivata parziale $\frac{\partial u}{\partial y}$.
Ovvero, andando a campionare i punti via via crescenti in $y$, la crescita lineare può essere caratterizzata geometricamente da una retta con pendenza $\frac{\partial u}{\partial y}$, che è uguale anche ad $\alpha_{3} $ .
Si chiama deformazione tagliante la somma delle due derivate.
Per piccoli spostamenti, ovvero quando è possibile assumere che angolo e tangente coincidano, la deformazione totale del cubetto, cioè lo spostamento angolare tra l’indeformata e la deformata vede un angolo che è $\alpha_{3} $ + $\alpha_{5} $ .
La deformazione a rombo viene caratterizzata come scostamento dalla forma quadrata di angolo:
$$ \alpha_{3} + \alpha_{5} = \gamma_{xy} $$
Cosa succede se $\alpha_{5} $ = - $\alpha_{3} $ , o viceversa?
Se andiamo a costruire la deformata del quadratino elementare con $\alpha_{5} $ e $\alpha_{3} $ che sono uguali ed opposti otteniamo semplicemente un quadratino ruotato.
Pertanto quando $\alpha_{3} $ = -$\alpha_{5} $ si ha una pura rotazione intorno all'asse $z$.
Matrice di legame spostamenti -> deformazioni
Abbiamo visto che esiste un legame tra $\varepsilon_{x}$, $\varepsilon_{y}$ e $\gamma_{xy}$ , e gli spostamenti $u_{i}$, $v_{i}$, $u_{j}$, $v_{j}$, $u_{k}$, $v_{k}$ dei tre nodi del triangolo.
Le deformazioni sono ricavate dagli spostamenti per differenziazione (la differenziazione è un operatore lineare).
In generale indico:
- il vettore colonna avente come componenti le deformazioni con $\mathbf{\varepsilon}$.
- il vettore che contiene i sei spostamenti dei sei gradi di libertà sul triangolo con $\mathbf{\delta}$ .
Il legame tra $\mathbf{\varepsilon}$ e $\mathbf{\delta}$ , essendo lineare, può essere rappresentato come una premoltiplicazione per matrice.
$\Rightarrow$ si può definire completamente questo legame lineare come una matrice, che chiamiamo $\mathbf{B}$, che premoltiplica $\mathbf{\delta}$.
Come si ricava $\mathbf{B}$?
Abbiamo visto che $\mathbf{\varepsilon}$ è funzione lineare delle incognite $\alpha_{1} $, … , $\alpha_{6} $. Le incognite $\alpha_{1} $, … , $\alpha_{6} $ sono funzioni lineari degli spostamenti. Combino le due funzioni lineari, e trovo una relazione lineare “combo” che posso esprimere nella forma della matrice $\mathbf{B}$.
La matrice $\mathbf{B}$ è una matrice che, ai fini della coerenza del prodotto matrice-vettore, deve essere una matrice a 6 colonne e 3 righe.
$$ \newcommand{\vec}[1]{\smash{\underline{#1}}} \newcommand{\mat}[1]{\smash{\underline{\underline{#1}}}} \begin{bmatrix}\varepsilon_{x} \\ \varepsilon_{y} \\ \gamma_{xy} \end{bmatrix} = \underbrace{ \frac{1}{2A} \begin{bmatrix} y_j - y_k & 0 & y_k - y_i & 0 & y_i - y_j & 0 \\ 0 & x_k - x_j & 0 & x_i - x_k & 0 & x_j - x_i \\ x_k - x_j & y_j - y_k & x_i - x_k & y_k - y_i & x_j - x_i & y_i - y_j \end{bmatrix} }_{\mat{B}} \begin{bmatrix} u_i \\ v_i \\ u_j \\ v_j \\ u_k \\ v_k \end{bmatrix} $$
Facendo un'analisi dimensionale degli elementi dell'equazione scritta in precedenza si nota che:
- le componenti del vettore $\mathbf{\delta}$ sono lunghezze [mm];
- le componenti del vettore $\mathbf{\varepsilon}$ sono delle variazioni di lunghezza su lunghezza, quindi sono numeri puri.
$\Rightarrow$ l'unità di misura degli elementi di $\mathbf{B}$ è [1/mm].
Se gli spostamenti sono lineari, le deformazioni (che sono le derivate degli spostamenti) devono essere per forza delle costanti; quindi $\varepsilon_{x}$ , $\varepsilon_{y}$ , $\gamma_{xy}$ non variano sull'elemento.
Se si verifica il caso in cui le deformazioni sono costanti lungo l'elemento, ma non costanti lungo il corpo, tra elemento ed elemento ci deve essere per forza una discontinuità deformativa.
Ovviamente poiché in generale i corpi non hanno stato deformativo uniforme, risulterà che, ad esempio, tra un elemento e l’altro le deformazioni saranno discontinue.
In particolare ho sempre una rappresentazione “a gradini” delle deformazioni.
Matrice di legame Tensioni -> Deformazioni
Una volta note le deformazioni, possiamo ricavare le tensioni. È possibile definire un legame tensioni-deformazioni che, nel caso specifico, è la legge di Hooke.
Sotto ipotesi di linearità, tensioni e deformazioni sono linearmente correlate. È quindi possibile scrivere $\sigma_{x}$, $\sigma_{y}$, $\tau_{xy}$ , che sono le tre componenti di tensione sul piano, come prodotto di una matrice, che qui chiamiamo $\mathbf{D}$, per il vettore delle deformazioni $\varepsilon_{x}$, $\varepsilon_{y}$ , $\gamma_{xy}$ :
$$ \newcommand{\vec}[1]{\smash{\underline{#1}}} \newcommand{\mat}[1]{\smash{\underline{\underline{#1}}}} \begin{bmatrix}\sigma_{x} \\ \sigma_{y} \\ \tau_{xy} \end{bmatrix} = {\mat{D}} \begin{bmatrix}\varepsilon_{x} \\ \varepsilon_{y} \\ \gamma_{xy} \end{bmatrix} $$
scritta in forma compatta $\boldsymbol{\sigma }=\boldsymbol{D}\boldsymbol{\varepsilon}$
$\boldsymbol{D}$ è una matrice 3×3 proporzionale al modulo di Young $E$.
Stati piani
La matrice di legame costitutivo legata al completo tridimensionale è una matrice 6×6, perchè lega le sei componenti nello spazio. Noi ne usiamo delle versioni ridotte, che sono matrici 3×3. Sono di base proporzionali al modulo di Young. Ne abbiamo a disposizione, per stati piani, una varietà, perchè una varietà sono i possibili stati piani che possiamo considerare.
Da notare che il solo concetto di stato piano è un'approssimazione, perchè nessun corpo con cui abbiamo a che fare ha natura piana, ma sono tutti quantomeno tridimensionali.
Quindi quando si parla di “stati piani” implicitamente bisogna introdurre qualche ipotesi semplificativa che riduca un corpo spaziale ad un problema piano.
Di matrici di stati piani ne abbiamo almeno due. Le due principali sono:
- matrice di legame costitutivo per stato di tensione piana;
- matrice di legame costitutivo per stato di deformazione piana.
Dopodichè abbiamo:
- stato di tensione-deformazione-spostamenti assialsimmetrici;
- stato di deformazione piana generalizzata.
Lo stato di tensione piana è costruito nell’ipotesi che tutte le componenti di tensione che coinvolgono contributi fuori piano siano nulle. Quindi lo stato di tensione piana vede la tensione fuori piano $\sigma_{z}$, uguale alla tensione tagliante con contributo fuori dal piano $\tau_{zx}$, uguale alla tensione tagliante con contributo fuori piano $\tau_{yz}$, uguali a zero:
$\sigma_{z}=\tau_{zx}=\tau_{yz}=0$
Stato di deformazione piana, viceversa, significa che le componenti di deformazione fuori piano sono nulle. Quindi la deformazione fuori piano $\varepsilon_{z}$ è uguale a zero, così come le deformazioni taglianti che coinvolgono un moto fuori piano $\gamma_{zx}$ e $\gamma_{yz}$:
$$\varepsilon_{z}=\gamma_{zx}=\gamma_{yz}=0$$
Lo stato di deformazione piana generalizzata si può scrivere, su una deformazione tagliante, come:
$$\gamma_{zx}=\gamma_{yz}=0$$
ma $\varepsilon_{z}$ lineare sul piano xy:
$$\varepsilon_{z}=\alpha_{7}+\alpha_{8}x+\alpha_{9}y$$
Diciamo che la deformazione piana generalizzata vede una deformazione in direzione normale al piano che non è costante, uguale a zero, ma è, ad esempio, lineare.
Questo stato lo abbiamo in genere in corpi traviformi, e $\alpha_{8}$ e $\alpha_{9}$ diventano curvature.
Un corpo tridimensionale è modellabile e approssimabile come un corpo soggetto a stato tensionale piano se per esso sono valide le seguenti ipotesi:
- è assimilabile a una figura piana estrusa fuori piano per uno spessore (esempio provino a osso di cane);
- il corpo è sottile (descritto completamente dalla sua proiezione su un piano) ed è caricato entro piano.
N.B. Se è caricato fuori piano non è possibile applicare una trattazione con stato piano. Sia geometria che caricamento devono essere descrivibili entro piano.
La relazione $\boldsymbol{\sigma }=\boldsymbol{D}\boldsymbol{\varepsilon}$ in caso di stato tensionale piano diventa
Forma deformazioni → tensioni
$$ \begin{bmatrix}\varepsilon_{x} \\ \varepsilon_{y} \\ \gamma_{xy} \end{bmatrix} = \cfrac{1}{E} \begin{bmatrix} 1 & -\nu & 0 \\ -\nu & 1 & 0 \\ 0 & 0 & 2(1+\nu) \end{bmatrix} \begin{bmatrix}\sigma_{x} \\ \sigma_{y} \\ \tau_{xy} \end{bmatrix} $$
Forma tensioni → deformazioni $$ \newcommand{\vec}[1]{\smash{\underline{#1}}} \newcommand{\mat}[1]{\smash{\underline{\underline{#1}}}} \begin{bmatrix}\sigma_{x} \\ \sigma_{y} \\ \tau_{xy} \end{bmatrix} = \underbrace{ \cfrac{E}{1-\nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \cfrac{1-\nu}{2} \end{bmatrix} }_{\mat{D}} \begin{bmatrix}\varepsilon_{x} \\ \varepsilon_{y} \\ \gamma_{xy} \end{bmatrix} $$
A questo punto abbiamo definito le tensioni e le deformazioni sull’elemento.
Le tensioni sono funzione lineare delle deformazioni. Le deformazioni sono costanti sull’elemento, quindi anche le tensioni sono costanti sull’elemento, nel caso triangolare a tre nodi.
Matrice di rigidezza per l'elemento triangolare
Il nostro obiettivo è quello di definire una matrice di rigidezza per l’elemento, ossia una matrice che leghi le sei componenti di forza nodale e le sei componenti di spostamento nodale.
Vogliamo quindi trovare la matrice $\mathbf{K}$ che leghi il vettore $\boldsymbol{F}$ alle componenti di spostamento (che costituiscono il vettore $\boldsymbol{\delta}$ ).
$$ \newcommand{\vec}[1]{\smash{\underline{#1}}} \newcommand{\mat}[1]{\smash{\underline{\underline{#1}}}} \underbrace{ \begin{bmatrix} F_{x,i} \\ F_{y,i} \\ F_{x,j} \\ F_{y,j} \\ F_{x,k} \\ F_{y,k} \end{bmatrix} }_{\vec{F}} = {\mat{K}} \underbrace{ \begin{bmatrix} u_i \\ v_i \\ u_j \\ v_j \\ u_k \\ v_k \end{bmatrix} }_{\vec{δ}} $$
Il nostro scopo è andare a costruire questa matrice $\mathbf{K}$. Per ora siamo arrivati a costruire le tensioni entro l’elemento.
Come procediamo?
Il problema è, sostanzialmente, trovare un’equivalenza tra le forze di cui sopra e le tensioni entro l’elemento.
Se ho uno stato tensionale definito entro l’elemento ho anche uno stato tensionale definito sul bordo.
$F_{x,k}$ e $F_{y,k}$ ad esempio potrebbero essere definiti in funzione della risultante delle azioni di tipo tensionale sul bordo. Potrebbe essere una definizione valida.
Io so che sul bordo ho delle $\sigma_{x}$, ho delle $\sigma_{y}$, e delle $\tau$; posso imporre che questa distribuzione di $\sigma$ e $\tau$ sia equilibrata dalle forze $F_{x}$, $F_{y}$ equivalenti sui due nodi.
Purtroppo una definizione di quelle forze per equilibrio delle tensioni di interfaccia sul lato definito tra i due nodi non è né univoca né efficace. Quindi quelle forze non sono le risultanti dello stato tensionale sul bordo.
L’equivalenza viene costruita in forma energetica.
Suppongo di avere un vettore spostamento nodale qualunque $\boldsymbol{\delta}$, e quindi implicitamente una qualunque configurazione deformata dell’elemento.
Questa configurazione deformata dà luogo ad un’energia potenziale elastica interna all’elemento, ossia un’energia potenziale elastica legata alla deformazione di ogni punto interno all’elemento.
Tuttavia, per imporre questa configurazione, servirà agire dall’esterno con delle forze. Quindi ci saranno delle forze esterne che compiranno lavoro.
Per qualunque configurazione deformata dell’elemento, descritta completamente da un vettore $\boldsymbol{\delta}$, posso ricavare un’energia potenziale elastica e un lavoro delle forze esterne;
queste ultime sono $F_{x,i}$, $F_{y,i}$, $F_{x,j}$, $F_{y,j}$, $F_{x,k}$, $F_{y,k}$, definite come quelle forze che è necessario applicare dall’esterno per mantenere l’elemento in quella configurazione deformata.
Il lavoro delle forze esterne, che possiamo chiamare lavoro esterno $L_{e}$, è uguale a:
$$ L_{e}=\frac{1}{2}{\vec{F}}^{T}{\vec{δ}} $$
Se definisco $\boldsymbol{F}$ come un vettore colonna, $\boldsymbol{F}^T$ è un vettore riga e moltiplicandolo per il vettore colonna $\boldsymbol{\delta}$ ottengo:
$$ L_{e}=\frac{1}{2} \begin{bmatrix} F_{x,i} & F_{y,i} & F_{x,j} & F_{y,j} & F_{x,k} & F_{y,k} \end{bmatrix} \begin{bmatrix}u_{i} \\ v_{i} \\ u_{j} \\ v{j} \\ u_{k} \\ v_{k} \\ \end{bmatrix} $$
Volendo estendere il prodotto riga per colonna:
$$ L_{e}=\frac{1}{2}(F_{x,i}u_{i} + F_{y,i}v_{i} + F_{x,j}u_{j} + F_{y,j}v{j} + F_{x,k}u_{k} + F_{y,k}v_{k}) $$
L’ $\frac{1}{2}$ è legato al fatto che sia il vettore $\boldsymbol{F}$ che il vettore $\boldsymbol{\delta}$ sono legati alla configurazione finale.
Tuttavia, nel passare dallo spazio inizialmente scarico alla configurazione finale, $\boldsymbol{F}$ e $\boldsymbol{\delta}$ sono cresciuti linearmente.
Il lavoro esterno finale è uguale all’integrale dall’istante $0$ al tempo $t$ della potenza istantanea.
La Potenza istantanea è legata alla forza $\boldsymbol{F}$, che è funzione del tempo, per un vettore velocità.
$$ L_{e}=\int_{0}^{t}{\vec{F}}(t){\vec{v}}\, dt = {\vec{F}_{medio}}{\vec{δ}} $$
Questa forza $\boldsymbol{F(t)}$ però non è una costante durante tutta l’operazione di caricamento, ma cresce linearmente durante la fase di carico, pertanto il valore integrato può essere considerato come il suo valore medio durate questa operazione.
A questo punto abbiamo la definizione del lavoro esterno in funzione di qualunque configurazione $\boldsymbol{\delta}$. Andiamo a vedere com’è il lavoro interno.
Il lavoro interno nasce dall’energia di deformazione elastica, che è definita punto per punto sull’elemento.
La densità di energia potenziale elastica è definita come:
$$ U=\frac{1}{2}{\vec{σ}}^{T}{\vec{ε}}\ $$
Anche qui $\boldsymbol{\sigma}$ ed $\boldsymbol{\varepsilon}$ sono valori a fine caricamento, a fine deformazione.
Questa è una densità, ossia un’ energia per unità di area (in quanto in questo caso siamo nel piano). Quindi per avere l’energia potenziale elastica su tutto l’elemento devo integrare su tutta l’area dell’elemento.
$\Rightarrow$ il lavoro interno, che è anche uguale all’energia potenziale elastica, è definito come:
$$ L_{i}=\int_{area}\frac{1}{2}{\vec{σ}}^{T}{\vec{ε}}\, da $$
A questo punto abbiamo sostanzialmente tutto quello che ci serve per calcolare, in funzione dello spostamento, l'energia interna.
In particolare sappiamo che:
$$ {\vec{ε}}={\mat{B}}{\vec{δ}} $$
Inoltre:
$$ {\vec{σ}}={\mat{D}}{\vec{ε}}={\mat{D}}{\mat{B}}{\vec{δ}} $$
Facendo il trasposto di $\boldsymbol{\sigma}$ abbiamo che:
$$ {\vec{σ}}^{T}=({\mat{D}}{\mat{B}}{\vec{δ}})^{T}={\vec{δ}}^{T}{\mat{B}}^{T}{\mat{D}}^{T} $$
Il lavoro interno è quindi uguale a:
$$ L_{i}=\frac{1}{2}\int_{area}{\vec{δ}}^{T}{\mat{B}}^{T}{\mat{D}}^{T}{\mat{B}}{\vec{δ}}\, da $$
Tale integrale è costante sull'elemento e risulta
$$ L_{i}=\frac{1}{2}a{\vec{δ}}^{T}{\mat{B}}^{T}{\mat{D}}{\mat{B}}{\vec{δ}}=\frac{1}{2}{\vec{F}}^{T}{\vec{δ}}=L_{e} $$
[N.B.: ${\mat{D}}={\mat{D}}^{T}$ essendo ${\mat{D}}$ simmetrica]
ponendo ${\vec{F}}^{T}{\vec{δ}}={\vec{δ}^{T}}{\vec{F}}$ in modo da semplificare i ${\vec{δ}^{T}}$ da entrambi i membri si ottiene:
$$ {\vec{F}}=a{\mat{B}}^{T}{\mat{D}}{\mat{B}}{\vec{δ}} $$
Avendo già definito ${\vec{F}}={\mat{K}}{\vec{δ}}$ possiamo quindi ricavare la matrice di rigidezza ${\mat{K}}$
$$
{\mat{K}}=a{\mat{B}}^{T}{\mat{D}}{\mat{B}}
$$
Si ricava così la matrice rigidezza $\mathbf{K}$ per l'elemento triangolare a tre nodi.
$\mathbf{K}$ è una matrice simmetrica 6×6 proporzionale al modulo di Young $E$ con rango variabile da 0 a 6 a seconda dei casi.
[N.B. rango → numero di autovalori non nulli]
In particolare per $\mathbf{K}$ il rango assume valore $6-3$, cioè $3$, poichè tre moti di corpo rigido (due traslazioni e una rotazione) danno forze nulle.
Perciò si hanno tre forme di spostamento nei nodi a cui è associata una forza elastica con autovalore nullo.
L'elemento elastico da noi considerato simula il movimento di una struttura, ma esso è legato ad altri elementi triangolati:
$\Rightarrow$ è necessario capire come passare dalla matrice $\mathbf{K}$ del singolo elemento alla rigidezza dell'intera struttura.
Tale matrice sarà costruita sulla base di un insieme di incognite che sono gli spostamenti degli elementi nodali della struttura.
Consideriamo la seguente struttura formata da tre elementi triangolari.
Il vettore degli spostamenti $\delta$ è il seguente $$ {\vec{δ}}={ \begin{bmatrix} u_1 \\ v_1 \\ u_2 \\ v_2 \\ u_3 \\ v_3\\ u_4 \\ v_4 \\ u_5 \\ v_5 \\ \end{bmatrix} } $$
Il vettore delle forze esterne da imporre sui nodi per mantenere in equilibrio il sistema è il seguente $$ {\vec{F}}={ \begin{bmatrix} F_{x,1} \\ F_{y,1} \\ F_{x,2} \\ F_{y,2} \\F_{x,3} \\ F_{y,3} \\F_{x,4} \\ F_{y,4} \\F_{x,5} \\ F_{y,5} \\ \end{bmatrix} } $$
Quindi possiamo scrivere $$ {\vec{F}_{strut}}={\mat{K}_{strut}}{\vec{\delta}_{strut}} $$
Bibliografia
- Antonio Strozzi, Costruzione di Macchine, Pitagora Editrice Bologna
- Antonio Strozzi, Dispensa: Progettazione assistita di strutture meccaniche