La caratteristica principale del costrutto di IF aritmetico è che all'interno delle parentesi si ha un risultato numerico e non un risultato logico, come invece avviene nella struttura semplice di IF dove la sequenza logica si basa sul True o False. Un'altra caratteristica è quella di avere una stringa a 3 vie, cioè 3 etichette che sono poste dopo aver definito la funzione da eseguire per ottenere il risultato numerico; Esempio:

     if ( b**2-4*a*c) 100,200,300
 100    print *, 'Roots are Complex'
     go to 400
 200    print *, 'Single Real Root' 
     go to 400
 300    print *, 'Two Real Roots'
 400 continue

Queste 3 etichette 100, 200, 300 successive ad IF hanno il seguente significato:
se l'espressione aritmetica (in questo caso il discriminante di un equazione di secondo grado) fornisce un valore inferiore a zero allora esegui la prima etichetta della stringa (in questo caso legge l'etichetta di riferimento 100 e va ad eseguire il comando con la medesima etichetta);
se l'espressione fornisce un valore uguale a zero allora esegui l'etichetta 200;
se l'espressione fornisce un valore maggiore di zero allora esegui l'etichetta 300.

Il comando go to 400 serve per saltare le righe di comando successive a quella appena eseguita e uscire dall'IF aritmetico.

Studiamo l'Input/Output su file mediante un esempio, con l'obiettivo di utilizzare una subroutine per il campionamento della funzione seno(x)/x entro un dato intervallo, concludendo con una successiva subroutine il quale, sulla base di tali campionamenti, calcoli l'integrale con la regola dei trapezi.
Bisogna per prima cosa definire la funzione, definire l'intervallo di integrazione e si campionerà questa funzione su “n” punti equispaziati lungo tale intervallo. Successivamente con questi campionamenti si calcolerà l'integrale utilizzando delle somme di aree e infine si restituirà il risultato a video.

In teoria, tale flusso logico potrebbe essere inserito interamente nel programma principale, ottenendo i medesimi risultati. Nonostante ciò, è comunque preferibile suddividere tali entità logiche in sottoprogrammi; in tal modo il programma, oltre a essere più leggibile, avrà in esso una serie di subroutine utilizzabili in futuro per altri programmi.
Inizilizziamo il primo programma:
program campiona

    implicit none
    double precision myfun, a , b , x , xi
    integer n , i
    write(*,*) 'inserire a,b,n'
    read(*,*) a, b, n
    write(*,*) 'campionamenti:'
    

dove:

• myfun è la funzione da campionare;
  
• a,b sono gli intervalli di campionamento;
  
• n sono le suddivisioni del campionamento;
  
• i indice per scorrere i campionamenti;
  

A questo punto vogliamo aprire il file, scriverci i campionamenti e salvare il file come campionamenti.txt; il comando da dare è:

    open( UNIT=10, FILE='campionamenti.txt', STATUS='NEW', ACCESS='SEQUENTIAL', FORM='FORMATTED')
    

dove:

1. UNIT = numero serve per dare un nome al file interno al programma. Si possono scegliere numeri da 1 a 99, esclusi 5 e 6 che sono riservati per stdin e stdout.
2. FILE = nomefile.txt apre il file considerato.
3. STATUS = NEW se il file è stato creato con il comando,
   STATUS = OLD se il file è stato già creato e lo sto modificando,
   STATUS = SCRATCH se il file è temporaneo, cioè viene creato per l'uso temporaneo del programma e poi viene cancellato.
4. ACCESS = SEQUENTIAL se il file viene letto rispettando l'ordine degli elementi (cioè ad esempio per leggere il trentesimo deve passare per i 29 elementi prima di questo);questa definizione è scelta di default se omessa;
   ACCESS = DIRECT se l'elemento nel file viene letto direttamente, senza dover passare per i precedenti; in quest'ultimo caso bisogna però obbligatoriamente definire la lunghezza che i record hanno per poter giungere a quello selezionato(per record si intendeono le informazioni registrate e si assumono di lunghezza costante), per fare ciò si aggiunge di seguito RECL = numero che indica appunto la lunghezza dei record.
   
5. ERR = numero indica di andare al label numero se ci sono problemi, quindi esce dal file.
6. FORM = FORMATTED indica che c'è un vincolo sulla formattazione delle cifre significative;questa definizione è scelta di default se omessa;
   FORM = UNFORMATTED indica che si utilizza la formattazione corrente, cioè la formattazione delle cifre così come appaiono in memoria.
   

Per quanto riguarda il FORM si può dire che entrambi vantano aspetti positivi e negativi. Lo standard di default FORMATTED, è semplice da leggere ed interpretare (es: file di testo leggibile dagli umani); gli svantaggi di quest'ultimo invece riguardano un'aspetto prevalentemente computazionale. FORMATTED ha una lettura di tipo sequenziale o “Accesso sequenziale”: legge i termini scorrendoli a partire dal primo, trovando nei separatori gli elementi di distinguo fra l'uno e l'altro. Tale procedimento purtroppo verrebbe svolto anche qualora si necessitasse di leggere solo gli ultimi 2 valori, aumentando in tal modo il numero di operazioni eseguite rispetto a quelle minime richieste. Un altro problema di tipo computazionale consiste nella memoria occupata dai singoli elementi. Un singolo carattere infatti può contenere molte di più delle 14 cifre da noi utilizzate. Il resto dello spazio rimane quindi inutilmente allocato. Sebbene non immediatamente interpretabile (una sequenza di byte), perché rappresenta l'immagine su disco di ciò che è presente in memoria , il form UNFORMATTED invece vanta un “comportamento” più efficace per quanto concerne l'aspetto computazionale es: se per ogni numero che scrivo vado a stoccare 8 byte, per andare a leggere l'ottavo numero salto i primi 56 byte e leggo i successivi 8 ( posso così spostare la testina del disco sull'ottavo elemento, anziché scorrere i primi 7 per arrivarvi) . “Scrivendo” le informazioni così come sono stoccate in memoria, tale form ci permette di “puntare” alla loro specifica posizione. In questo modo si può “saltare” da una cifra all'altra senza difficoltà ed in maniera più immediata, perché è nota a priori la lunghezza delle cifre precedenti (ad esempio se ho dei numeri reali in singola precisione ognuno di essi occupa 4 byte). Tale comportamento è chiamato ad “Random Access” o “Accesso Casuale”, tuttavia random non sta a significare una vera e propria selezione casuale, ma significa che posso puntare una qualsiasi slot (casella). Di default, la forma utilizzata è la FORMATTED.

Da questa distinzione appena descritta derivano le due scelte di utilizzo: FORMATTED SEQUENTIAL (scelta di default, se omessa) e UNFORMATTED DIRECT.

Il comando OPEN obbliga l'utilizzo di un comando CLOSE(valore unit) per chiudere il file.

Proseguiamo con il programma:

    do i=0,n
     xi = dble(i)/dble(n)
     x= a * (1.0d0 - xi) + b * xi
     write(10,*) x , myfun(x)
    enddo
    
    close(UNIT=10)
    
    stop
    end

dove:

• write(10,*) va a scrivere nel file chiamato con UNIT=10 i risultati ottenuti di x e di myfun.
  
• dble viene utilizzato per convertire un intero in doppia precisione.
  

Continuiamo con il programma:

    double precision function myfun(x)
    implicit none
    double precision x
    if ( x .GT. 0.0d0 ) then
     myfun=dsin(x)/x
    else
     myfun=1.0d0
    endif
    return
    end

dove :
seno(x) viene scelto in doppia precisione per omogeneità dei risultati, avendo definito tutto il programma in doppia precisione e per non lasciare l'overloading al programma (cioè la scelta della precisione viene fatta dal compilatore);
Programma completo a questo link campiona.for
Qui http://www.obliquity.com/computer/fortran/intrinsic.html è possibile scegliere la sintassi per tutte le funzioni.
Questo file invece testaccform.for è stato utilizzato per trovare quale fosse la scelta di default tra FORMATTED e UNFORMATTED (CHE abbiamo visto essere FORMATTED).

Andiamo adesso a scrivere il secondo programma, che andrà a leggere il file campionamenti.txt e svolgerà l'integrale con il metodo dei trapezi:

    program integra
    implicit none
    double precision xnew,ynew,xold,yold,accumulo
    integer i

Accesso sequenziale, formato formatted di default

    open(UNIT=10,FILE='campionamenti.txt',STATUS='OLD')

Inizializzo variabile di accumulo a valore nullo

    accumulo=0.0d0

Inizializzo variabile contatore campionamenti letti

    i=0

Ciclo sommando contributi alla variabile di accumulo

 20 continue
    read(UNIT=10, FMT=* , END=100) xnew , ynew
    i=i+1
    if ( i .GE. 2 ) then
      accumulo = accumulo + (xnew-xold) * (ynew+yold)/2.0d0
      write(*,*) i
    endif
    xold=xnew
    yold=ynew
    goto 20

Finiti i contributi, stampo a video i risultati

100 write(*,*) accumulo
    stop
    end

dove:
read(UNIT=10, FMT=* , END=100) xnew , ynew legge il file contrassegnato con UNIT=10 (cioè quello appena creato con i campionamenti), dove END=100 ha la funzione di far uscire dal ciclo quando andrò a leggere un elemento che non è nel file (se non ci fosse questo END=100 il ciclo non avrebbe una fine in quanto non è indicata un arresto per l'indice i).
Osservo che il numero di contributi = numero di righe lette - 1, perchè i punti di campionamento sono uno in più; per questo motivo mi serve un contatore i.
Inoltre le prime due coordinate che leggo vengono prese come estremi per costruire il trapezio successivo (per queso c'è la denominazione new e old);
Otteniamo così l'accumulo eseguito e il risultato dell'integrale con il metodo dei trapezi: https://cdm.ing.unimo.it/dokuwiki/_media/wikipaom2015/schermata_del_2015-03-20_17_54_22.png

Esistono in rete delle librerie di riferimento in cui è possibile trovare molti programmi svolti. Le più famose sono:

LAPACK (Contiene operazioni matriciali, calcolo di rango, determinante ecc.)

BLAS (contenente operazioni matriciali)

LAPACK (Linear Algebra PACKage) è un insieme di librerie software usate per effettuare calcoli scientifici ad alto livello. Tali librerie sono state scritte in Fortran 77 e sono di dominio pubblico, anche se esistono delle personalizzazioni di queste librerie a pagamento. L'ultima versione è la 3.5.0 del 16 novembre 2013. Mediante queste librerie, è possibile effettuare calcoli di notevole importanza, come il calcolo di autovalori ed autovettori di matrici, risoluzione di sistemi lineari, fattorizzazioni di matrici, e molto altro ancora. Ad esempio, esistono delle procedure interne, nascoste all'utente, in grado di trasformare la matrice iniziale in una matrice tridiagonale, per poi calcolare effettivamente autovalori ed autovettori. Come dipendenza questa libreria richiede l'installazione di un'altra libreria: la BLAS (Basic Linear Algebra Subprograms). Le procedure all'interno di tale libreria consentono di effettuare calcoli scientifici di più basso livello, come il calcolo del prodotto scalare tra due vettori, prodotto matrice per vettore, etc.

BLAS (Basic Linear Algebra Subprograms) sono routine standard che forniscono elementi di base per l’esecuzione delle operazioni su vettori e matrici. Il Livello 1 di BLAS esegue operazioni scalari, vettoriali e vettore-vettore, il Livello 2 di BLAS esegue operazioni matrice-vettore, e il Livello 3 di BLAS risolve operazioni matrice-matrice. Poiché BLAS risulta particolarmente efficiente, portatile, e ampiamente disponibile, è comunemente usata per lo sviluppo di software di algebra lineare di alta qualità.

Esempio di utilizzo librerie Lapack, che utilizza la subroutine ZGEEV:

     Program Eigenvalue

c finding the eigenvalues of a complex matrix using LAPACK

     Implicit none

c declarations, notice double precision

      complex*16 A(3,3), b(3), DUMMY(1,1), WORK(6)
      integer i, ok

c define matrix A

     A(1,1)=(3.1, -1.8)
     A(1,2)=(1.3, 0.2) 
     A(1,3)=(-5.7, -4.3)
     A(2,1)=(1.0, 0)
     A(2,2)=(-6.9, 3.2)
     A(2,3)=(5.8, 2.2)
     A(3,1)=(3.4, -4.0)
     A(3,2)=(7.2, 2.9)
     A(3,3)=(-8.8, 3.2)

c c find the solution using the LAPACK routine ZGEEV

      call ZGEEV('N', 'N', 3, A, 3, b, DUMMY, 1, DUMMY, 1, WORK, 6, 
    $WORK,ok)

c c parameters in the order as they appear in the function call c no left eigenvectors, no right eigenvectors, order of input matrix A, c input matrix A, leading dimension of A, array for eigenvalues, c array for left eigenvalue, leading dimension of DUMMY, c array for right eigenvalues, leading dimension of DUMMY, c workspace array dim>=2*order of A, dimension of WORK c workspace array dim=2*order of A, return value c c output of eigenvalues

     if (ok .eq. 0) then
     do i=1, 3
     write(*,*) b(i)
     enddo
     else
     write (*,*) "An error occured"
     endif
     end

Compilare il codice di cui sopra,con il seguente comando(previa installazione delle librerie lapack):
gfortran provalapack.for -llapack && ./a.out

Nota: quando utilizziamo delle librerie esistenti bisogna stare attenti a tutte le variabili e subroutine definite ma che sono sovrabbondanti per i nostri scopi, quindi si preferisce richiamare il programma già compilato con il comando call.
Nel nostro esempio si può vedere nella subroutine ZGEEV le molteplici variabili che sono definite: http://www.netlib.org/lapack/explore-3.1.1-html/zgeev.f.html
Questo è il file dell'esempio visto che trova gli autovalori di una matrice complessa:provalapack http://www.physics.orst.edu/~rubin/nacphy/lapack/codes/eigen-f.html

FINE PARTE FORTRAN DEL CORSO

Nel seguito andiamo a determinare la matrice di rigidezza K di una molla con due carichi applicati alle rispettive estremità della stessa che deformano la molla allungandola.
Definiamo gli estremi della molla in configurazione indeformata tramite la seguente coppia di coordinate:
$$ (x_i,y_i),(x_j,y_j) $$ Successivamente definiamo gli estremi della molla in configurazione deformata:
$$ (x_i+u_i,y_i+v_i),(x_j+u_j,y_j+v_j) $$ A questo punto calcoliamo la differenza tra gli estremi così da trovare l'allungamento della molla (dl):


Adesso calcoliamo l'energia potenziale U della molla in configurazione deformata tramite la seguente formula:
$$ U=1/2\delta ^TK\delta $$ dove:

• δ è il vettore degli spostamenti nodali:

$$ \delta =\begin{bmatrix} u_i\\ v_i\\ u_j\\ v_j \end{bmatrix} $$

• K matrice di rigidezza.
  

Quindi potrei scriverla come:
$$ U=\frac{1}{2}\sum_{i}\sum_{j}K_{ij}\delta_{i}\delta_{j} $$ Allora possiamo scrivere l'energia potenziale elastica U tramite la sua espansione di Taylor arrestata al secondo ordine, ricordando la seguente definizione:

A second-order Taylor series expansion of a scalar-valued function of more than one variable can be written compactly as $$ T(\mathbf{x}) = f(\mathbf{a}) + (\mathbf{x} - \mathbf{a})^\mathrm{T} \mathrm{D} f(\mathbf{a}) + \frac{1}{2!} (\mathbf{x} - \mathbf{a})^\mathrm{T} \,\{\mathrm{D}^2 f(\mathbf{a})\}\,(\mathbf{x} - \mathbf{a}) + \cdots $$

where $ D f(\mathbf{a}) $ is the gradient of $f$ evaluated at $\mathbf{x} = \mathbf{a}$ and $D^2 f(\mathbf{a})$ is the Hessian matrix.
Nel nostro caso sarà:

• T(x) è l'energia potenziale elastica U(x);
• La matrice rigidezza K è invece l'Hessiana H(x), dove
  

$$ \begin{bmatrix} H \end{bmatrix}_{ij}=\frac{\partial F}{\partial x_{i}}\frac{\partial }{\partial y_{i}}\begin{bmatrix} H \end{bmatrix}_{ij} $$ valutato in x=a
Proseguiamo quindi imponendo che K sia una matrice nulla per poi assegnare gli elementi:

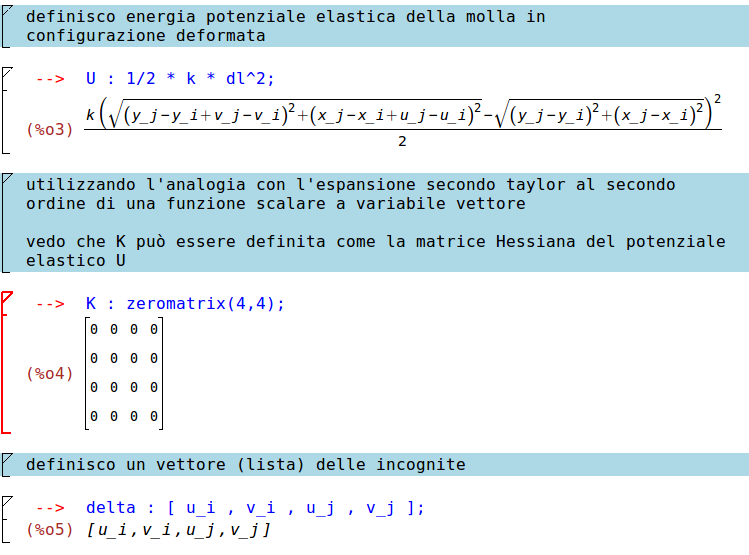
Nota: l'espansione in serie di Taylor viene eseguita attorno alla configurazione di equilibrio, cioècon il sistema scarico.\\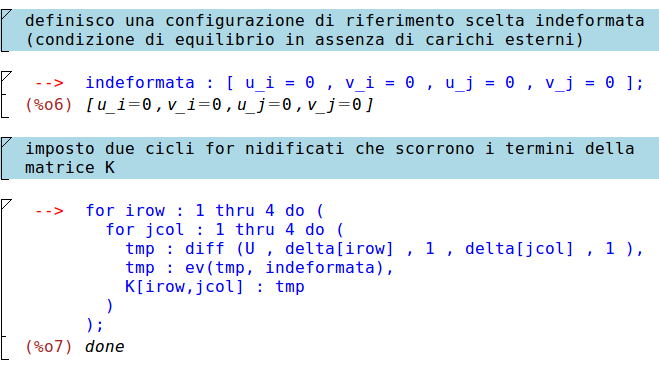
dove nei cicli nidificati il passo di avanzamento di lettura elementi è 1 (step 1) che è stato omesso in quanto sottinteso.
Se avessimo voluto visualizzare tmp prima di valutarlo con l'indeformata avremmo dovuto scrivere disp(tmp).
Possiamo adesso visualizzare la matrice di rigidezza K, trovata utilizzando il teorema di Schwarz, il quale afferma che (sotto opportune ipotesi) l'ordine con il quale vengono eseguite le derivate parziali in una derivata mista di una funzione a variabili reali è ininfluente.

Programma a questo link kmolla.wxmx

block ( [ v_1 , … , v_m ] , expr_1 , … , expr_n )

Blocco valuta expr_1 , … , expr_n in sequenza e restituisce il valore dell'ultima espressione valutata . La sequenza può essere modificata per andare a…, fino a… , e ritorna alla funzione… .
L' ultima espressione valutata è expr_n, a meno che è presente 'ritorna a …', o un'espressione contenente 'per andare a…'.
Alcune variabili v_1 , … , v_m possono essere dichiarate localmente al blocco ; queste si distinguono dalle variabili globali che hanno lo stesso nome. Se non sono dichiarate variabili locali, allora la lista può essere omessa.
All'interno del blocco qualsiasi variabile diversa da v_1 , … , v_m è una variabile globale.
NB:

block(… , … , …)

e semplicemente

(… , … , …)

non sono forme equivalenti, ma si differenziano ad esempio nel fatto che la seconda non gestisce l'eventuale natura locale delle variabili.
File esempio di verifica variabili locali blocco: test_variabili_locali_blocco.wxmx

Bibliografia e Approfondimenti:
http://www.star.le.ac.uk/~cgp/prof77.html

http://www.obliquity.com/computer/fortran/

http://www.idris.fr/data/cours/lang/fortran/F77.html