geometria piede di biella originaria

• modello in tensione piana
• spessore piede 12 mm
• spessore tasca 6 mm
• acciaio

modello cattedra a fine lezione scorsa

modello completo solo forzamento

modello completo con link per altri casi di carico

file txt estratti sul path plot al bordo interno del piede per i tre casi di:

• forzamento con interferenza 0.03 mm forz.txt
• carico trattivo (distribuzione pressione alla Demidov-Kolkin) di 10kN traz.txt
• carico compressivo (distribuzione pressione alla Giovannozzi) di 10kN comp.txt

foglio di calcolo per elaborazione elaborazione_dati_piede_biella.ods elaborazione_dati_piede_biella.xls

Riprendiamo dal file della lezione precedente: piede_biella, il quale contiene la modellazione della biella e della bronzina.
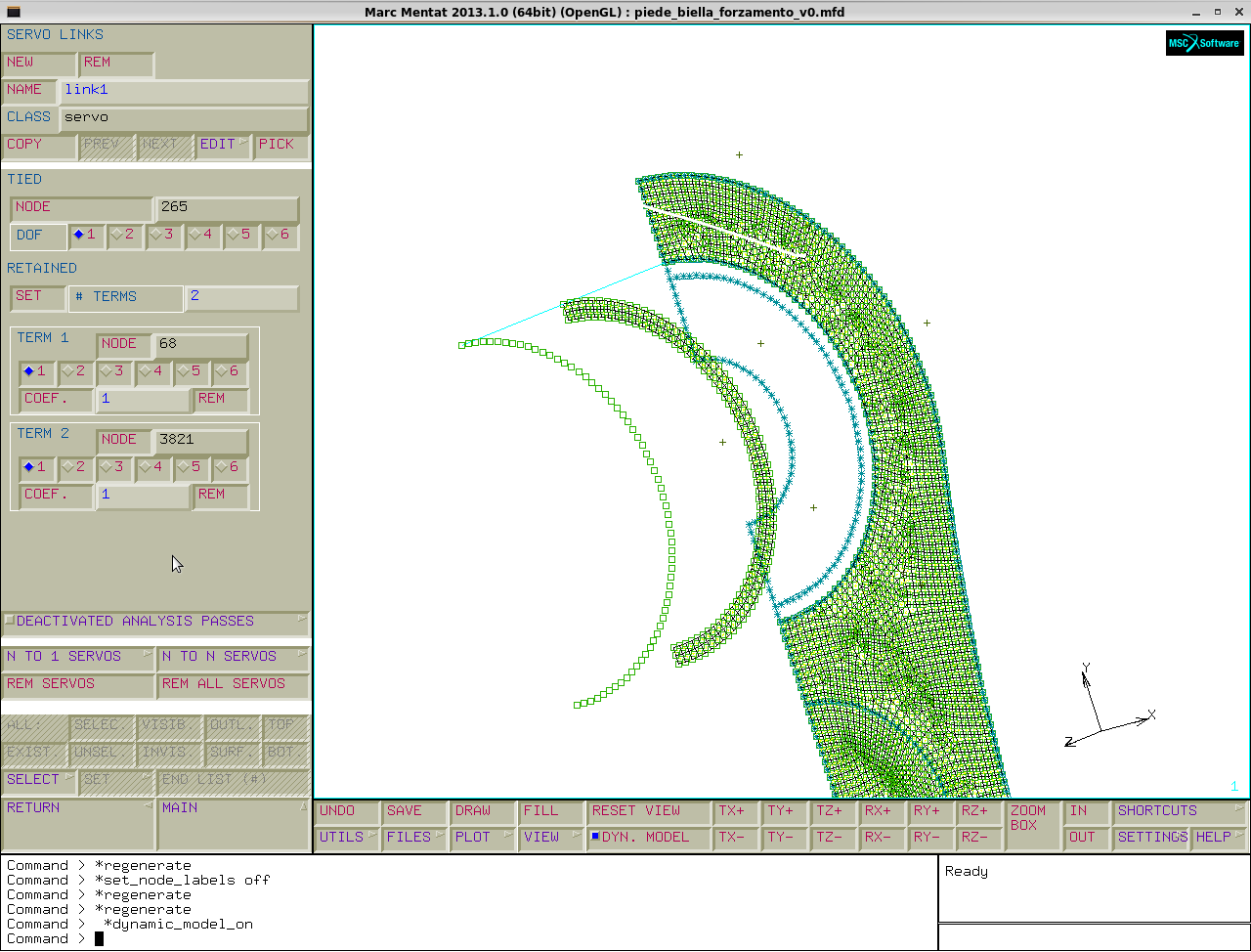
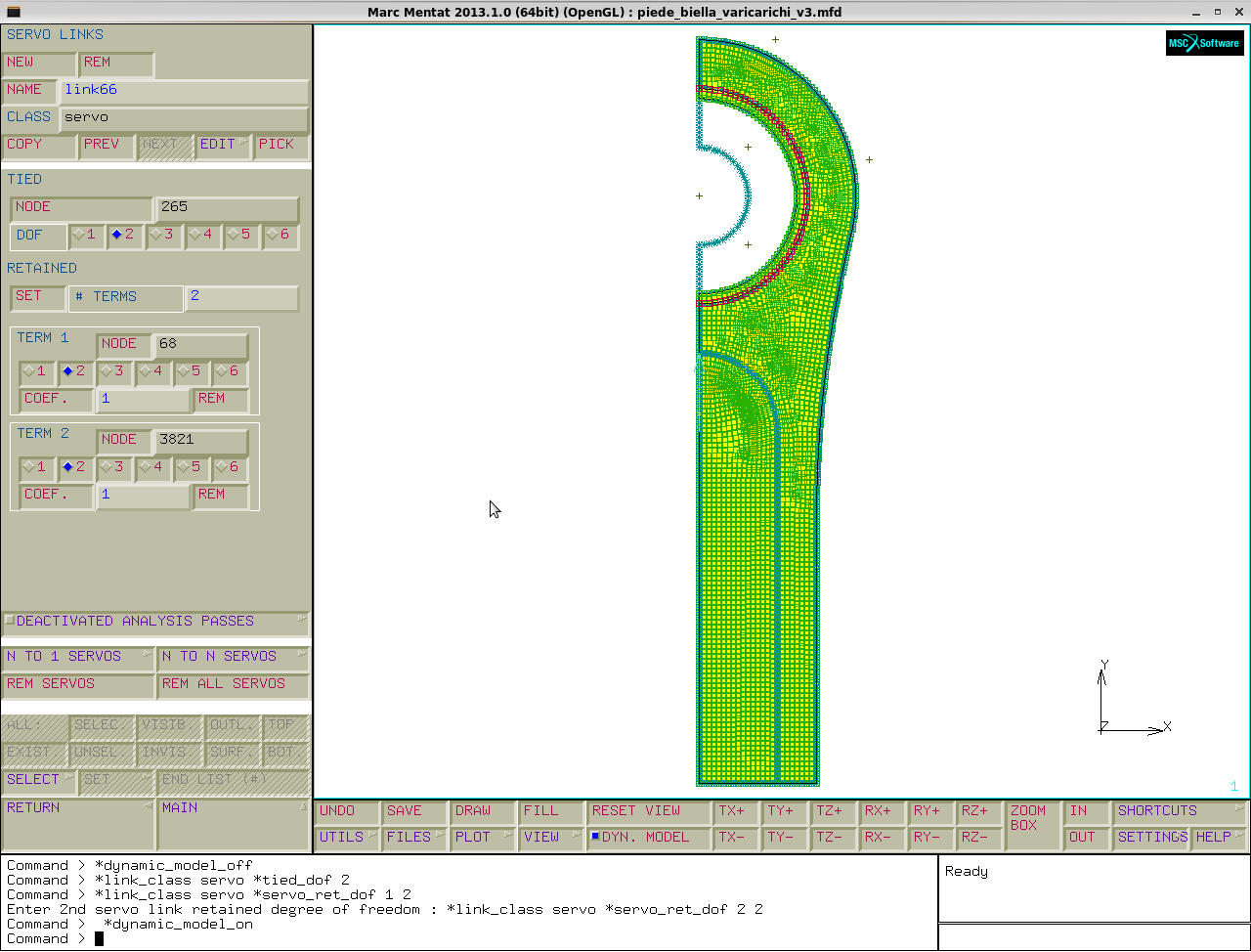
Avevamo già creato il servo link necessario a vincolare lo spostamento radiale del nodo 265 appartenente al piede, rispetto al nodo 68 della bronzina e al nodo 3821 dell' anello ausiliario tramite la relazione : $U_{265}=1*U_{68}+1*U_{3821}$.

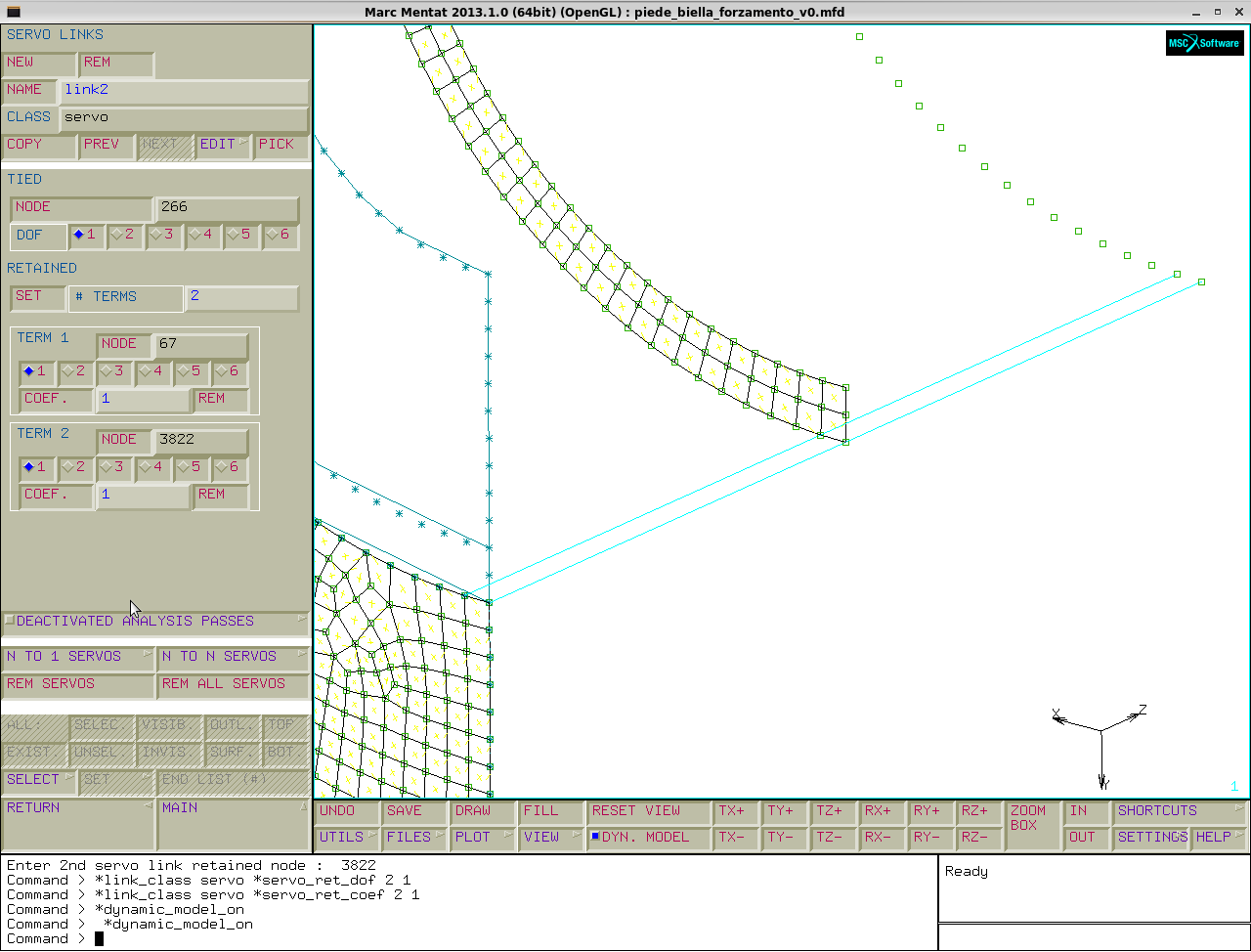
Si ripete la procedura per creare un servo link sul nodo successivo:
menu→link→servo link→new→tied→seleziono il nodo 266 sul piede e compilo la tabella come nell' immagine sotto mostrata, nella quale si vincola il primo g.d.l. del nodo 266 ai primi g.d.l. dei nodi 67 (bronzina) e 3822 (aux) tramite la relazione: $U_{266}=1*U_{67}+1*U_{3822}

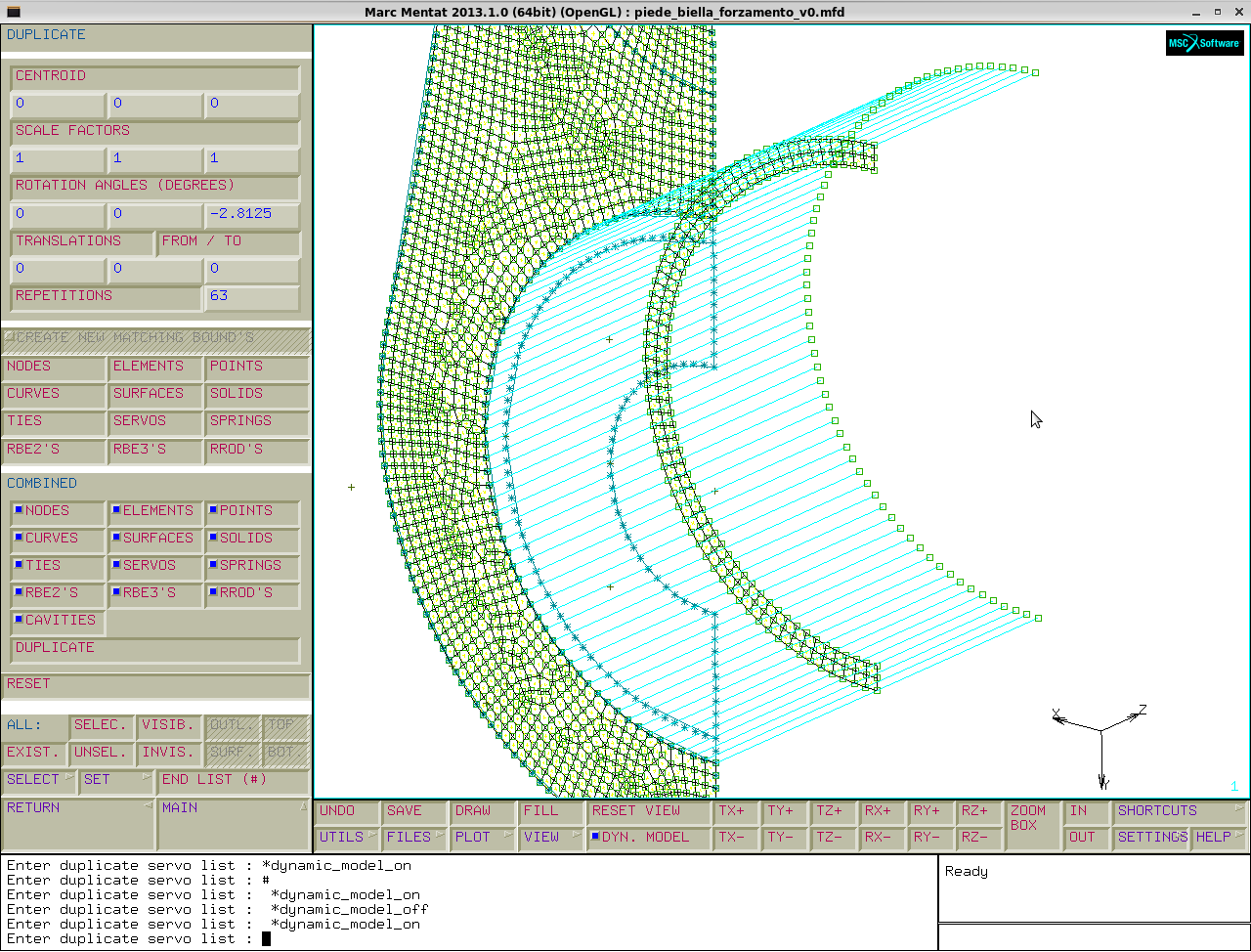
Si ripete il servo link per tutto l' anello interno del piede con la funzione duplicate:
menu→mesh generation→DUPLICATE (conviene schiacciare reset per pulire da operazioni precedenti)→rotation angles (0, 0, -180/64)→repetitions 63→servos:seleziono il secondo servo link→end list.

Dopo questa operazione si potrebbero avere nodi sovrapposti, allora si utilizza lo SWEEP con tolleranza 1/100 selezionando tutti (all) i nodi.

Così abbiamo duplicato i nostri link.
Ora dobbiamo definire il sistema di coordinate cilindrico:
menu→boundry conditions→transformations→coordinate system (permette di creare diversi sistemi di riferimento globali)→new→name:sistema_cilindrico→type:cylindrical→A(0,0,0);B(0,0,1);C(0,11,0).
Con:

• A=coordinata dell' origine
  
• B=punto qualunque sull'asse z
  
• C=punto per cui l' angolo del sistema cilindrico vale 0.

Ora dobbiamo associare il sistema cilindrico ai nodi di nostro interesse, per farlo risulta comodo far vedere solo quelli nascondendo gli altri:
plot→elements→settings→disattivo le facce e metto gli edges in outline (fa vedere solo quelli di bordo).

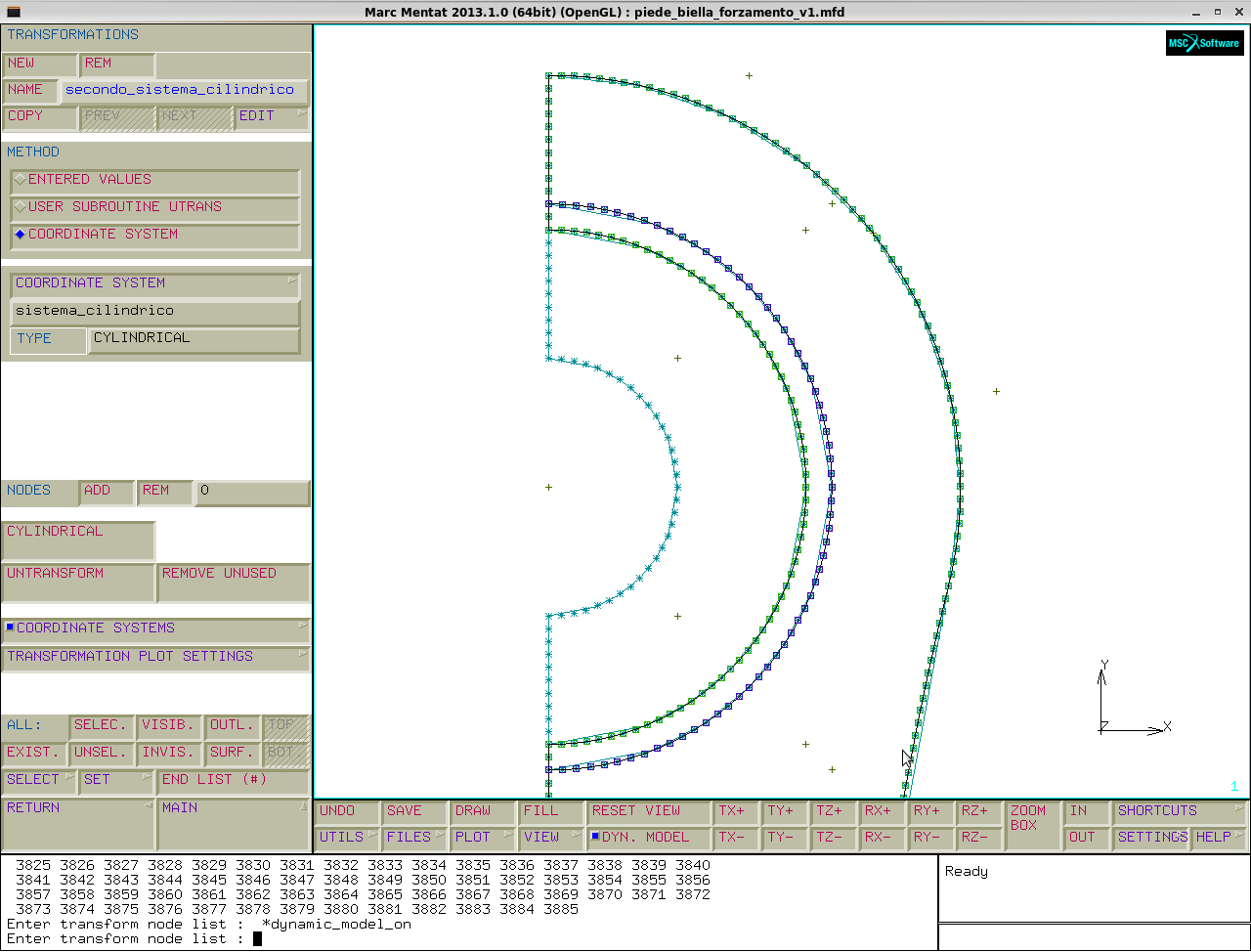
Ora andiamo su :
transformations→new→name:secondo_sistema_cilindrico→method:coordinate system→seleziono quello appena creato→inseriamo tutti i nodi associati ai link,con selezione poligonale (nodi evidenziati in figura)→end list.

Si procede ora con l' assegnazione delle boundry conditions; per il momento facciamo solo il calcolo del forzamento.
VINCOLO DI SIMMETRIA: servono due diversi tipi di vincolamento visto che abbiamo nodi con diverso sistema di riferimento.
Creiamo il primo:
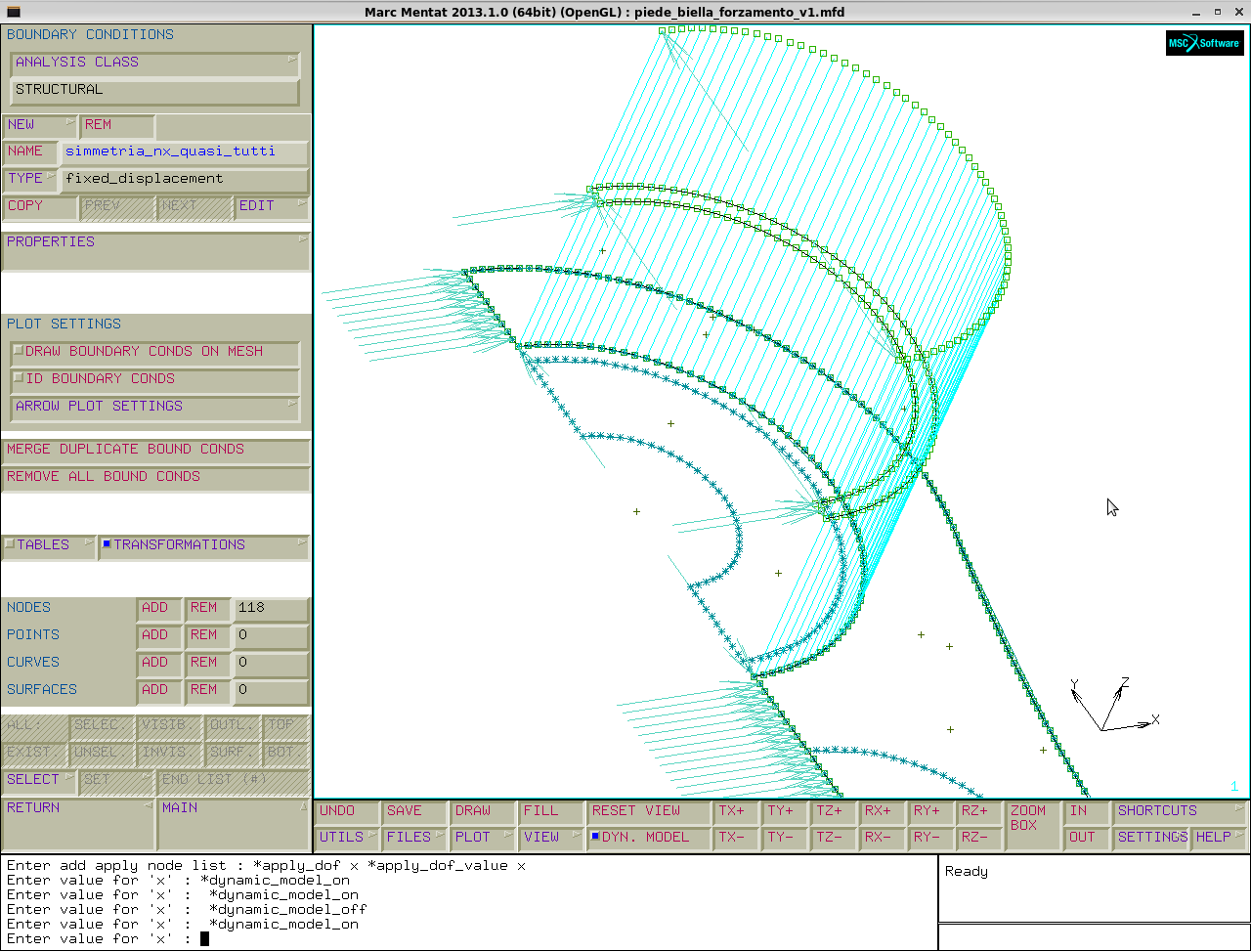
boundry conditions→new→name:simmetria_quasi_tutti→type: fixed displacement→properties:displacement x=0→nodes→add: seleziono solo la prima linea di nodi.

Però, come già detto, ciò non va bene per i nodi a cui è stato assegnato il sistema di riferimento cilindrico, quindi rimuovo questi nodi con nodes→remove→posso selezionare i nodi a mano, oppure utilizzare select by→transformations.
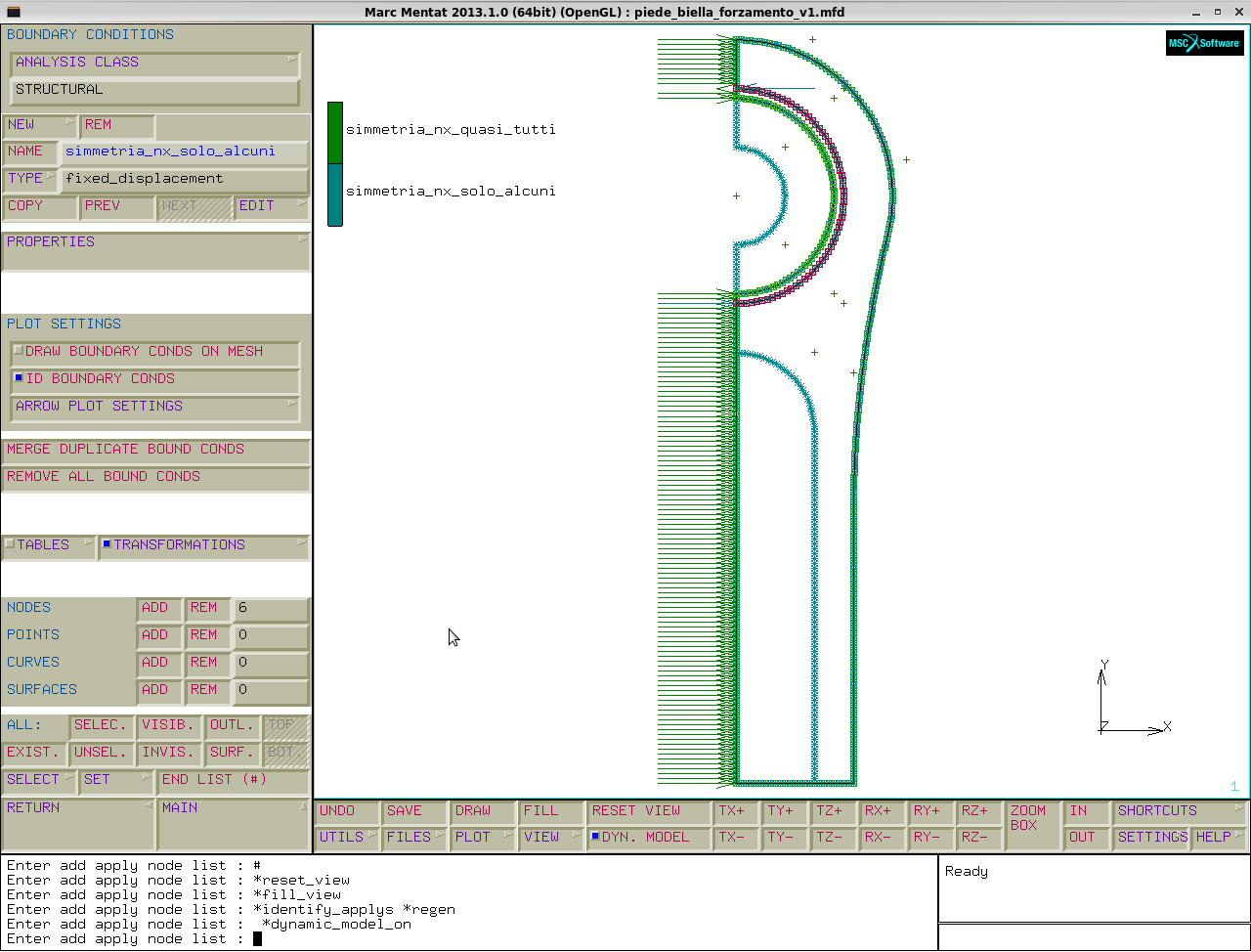
Ora blocchiamo il g.d.l. circonferenziale per i nodi col sistema di coordinate cilindrico:
boundry conditions→new→name: simmetria_solo_alcuni→fixed displacement→properties:displacement y=0 (è il secondo g.d.l, che per il sistema cilindrico corrisponde allo spostamento circonferenziale)→add nodes: seleziono i 6 nodi interessati→end list.

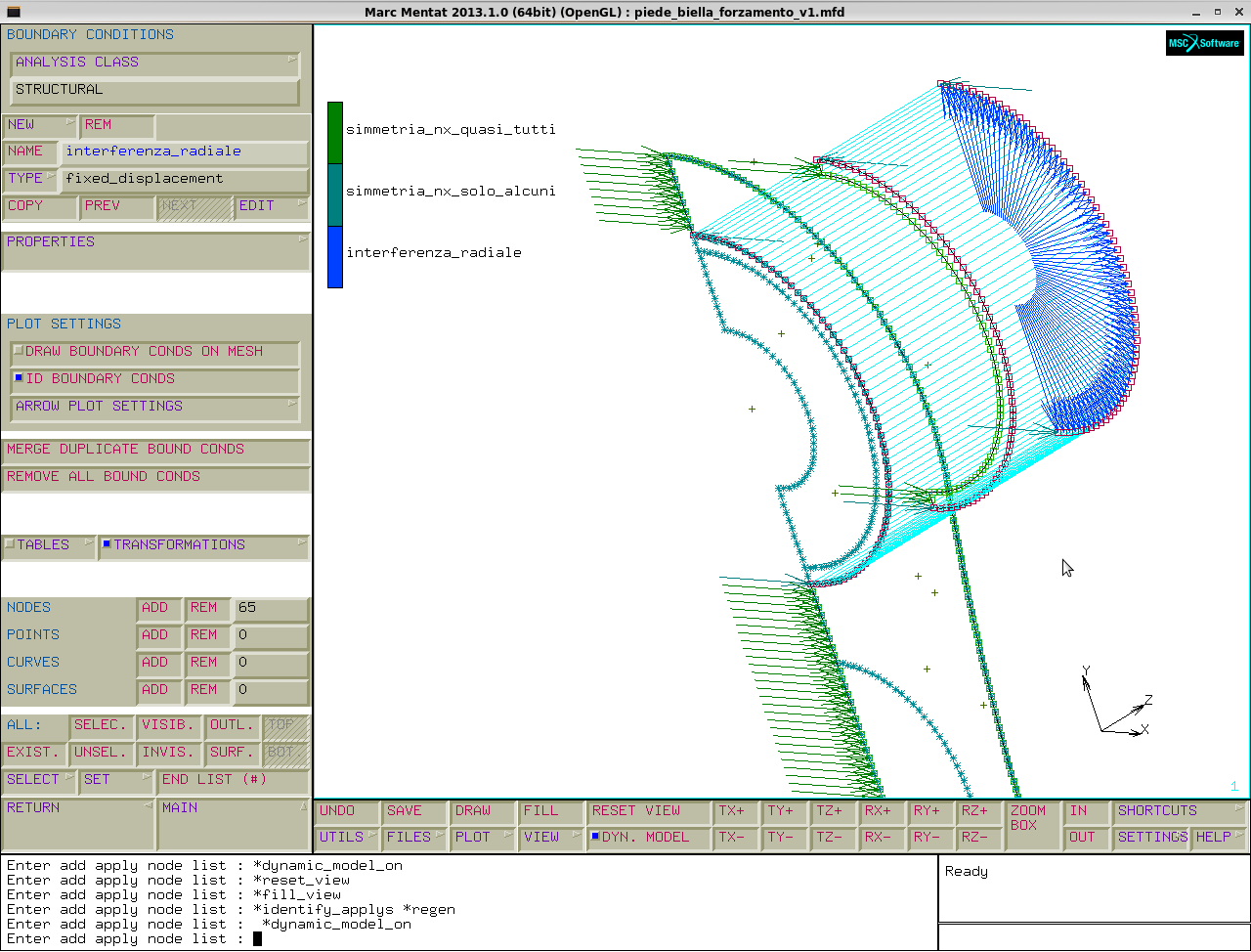
Ora creo la boundry conditions corrispondente alla INTERFERENZA tra bronzina e piede:
boundry conditions→name: INTERFERENZA_RADIALE→fixed displacement→properties:displacement x=0.03→ nodes→add:associo tutti i nodi ausiliari→end list.

Infine occorre eliminare i moti di corpo rigido residui, che nel nostro caso si riducono al solo spostamento lungo l' asse y.
Per eliminare questo moto di corpo rigido mi basta fissare solo uno dei due corpi, perchè questi sono collegati dai links:
boundry conditionsnew→name: posizionamento_y→properties: displacement y=0→nodes→add: seleziono un punto della biella (sarebbe meglio un punto scarico)→end list.

A questo punto si può lanciare il calcolo:
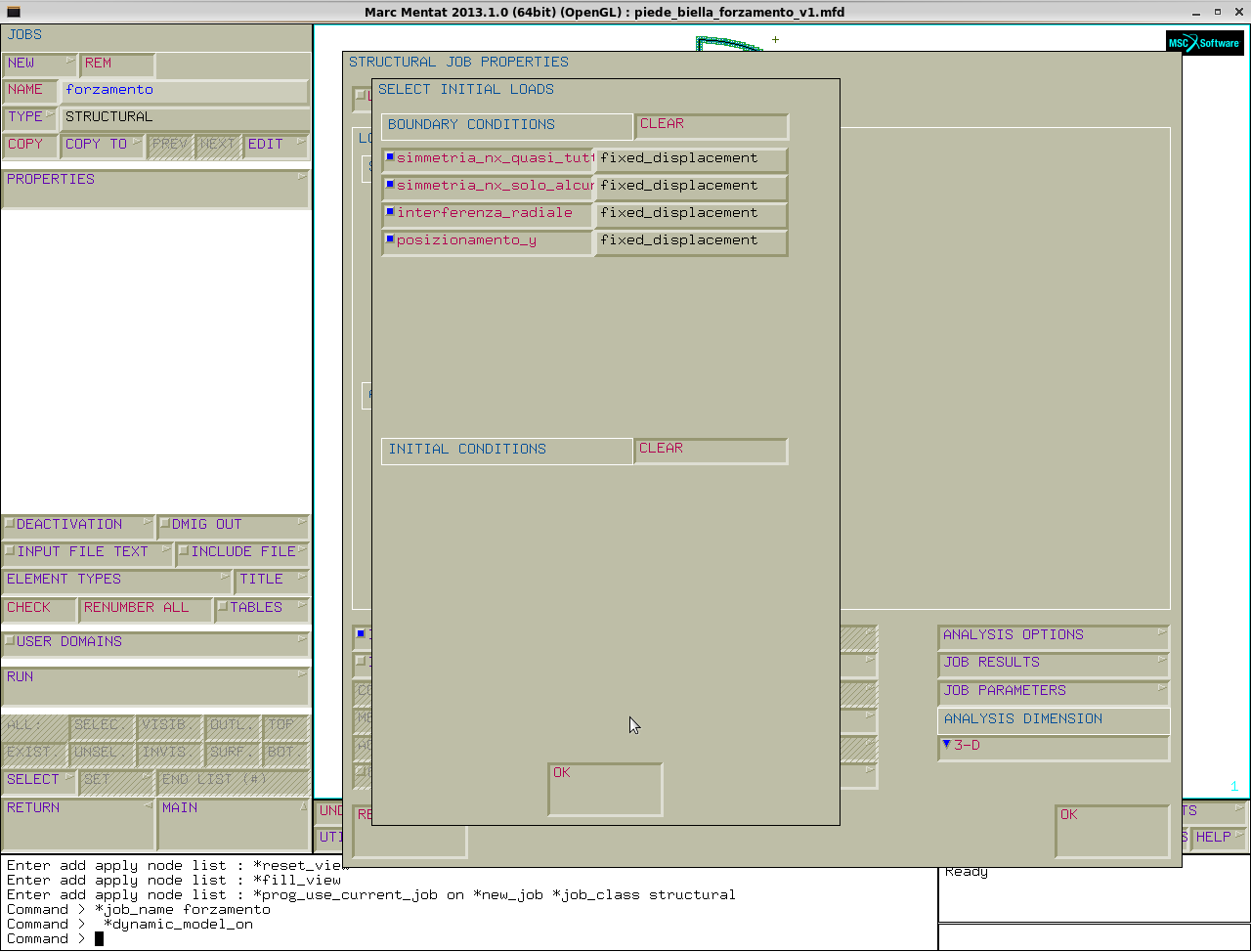
jobs→new→name:FORZAMENTO→properties:si selezionano tutti gli initial loads presenti→run.

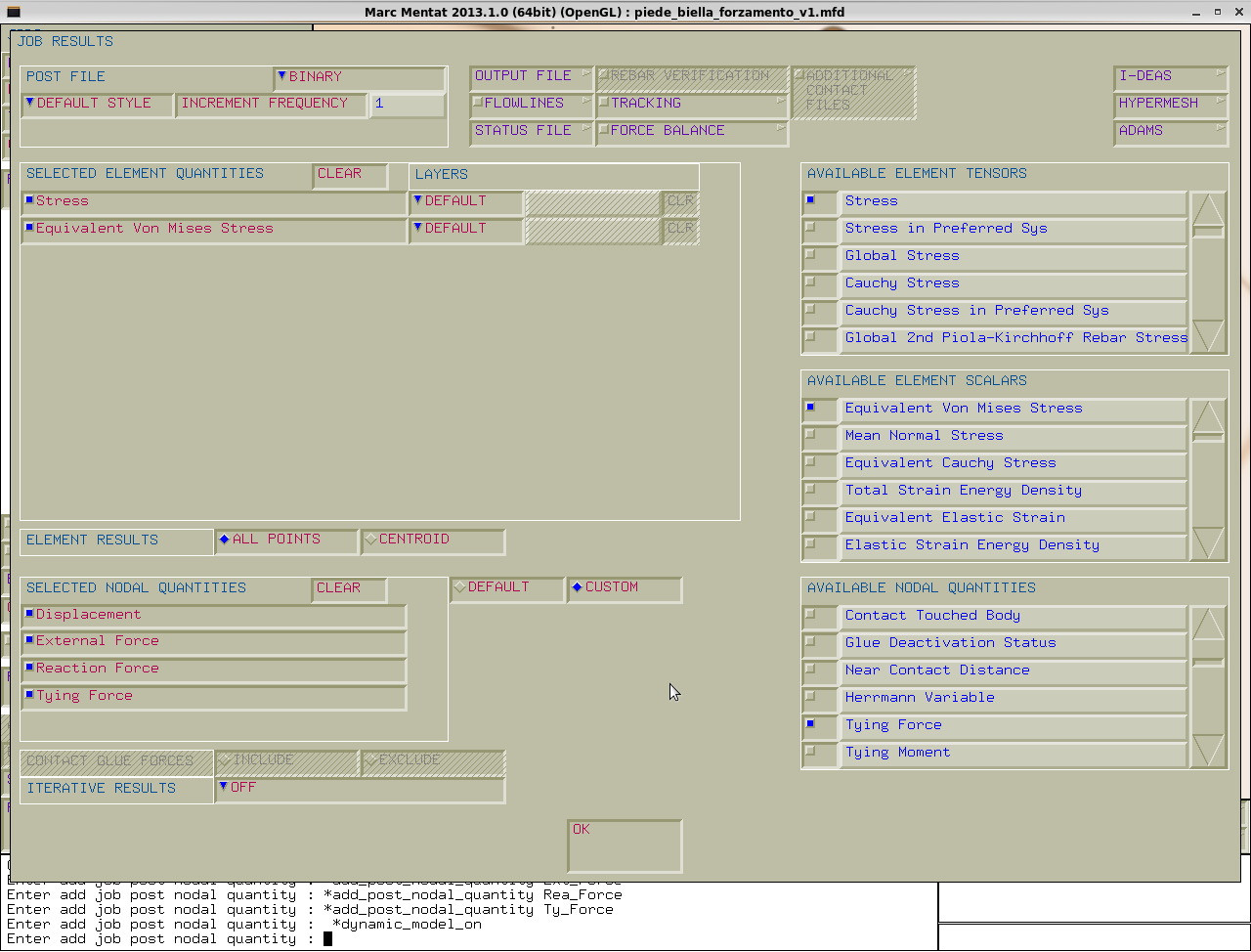
I risultati richiesti sono gli stress e l' equivalent von mises stress, mentre per le quantità nodali selezionate sono: displacement, external force, reaction force, tying force (sono le forze che i vincoli applicano alla struttura).

Potrebbe esserci un problema se si mettesse lo spostamento tangenziale dell' ausiliario tra le incognite, in quanto potrebbero esserci singolarità nella matrice, questo perchè l' ausiliario aggiunge altre incognite al problema.
Se il marc lavora bene non è necessaria nessuna operazione, altrimenti occorre imporre gli spostamenti tangenziali dell' ausiliario nulli.
Nel nostro caso non si sono verificati problemi, quindi si procede con l' analisi dei risultati.
RISULTATI:
conviene guardare piede e bronzina singolarmente:
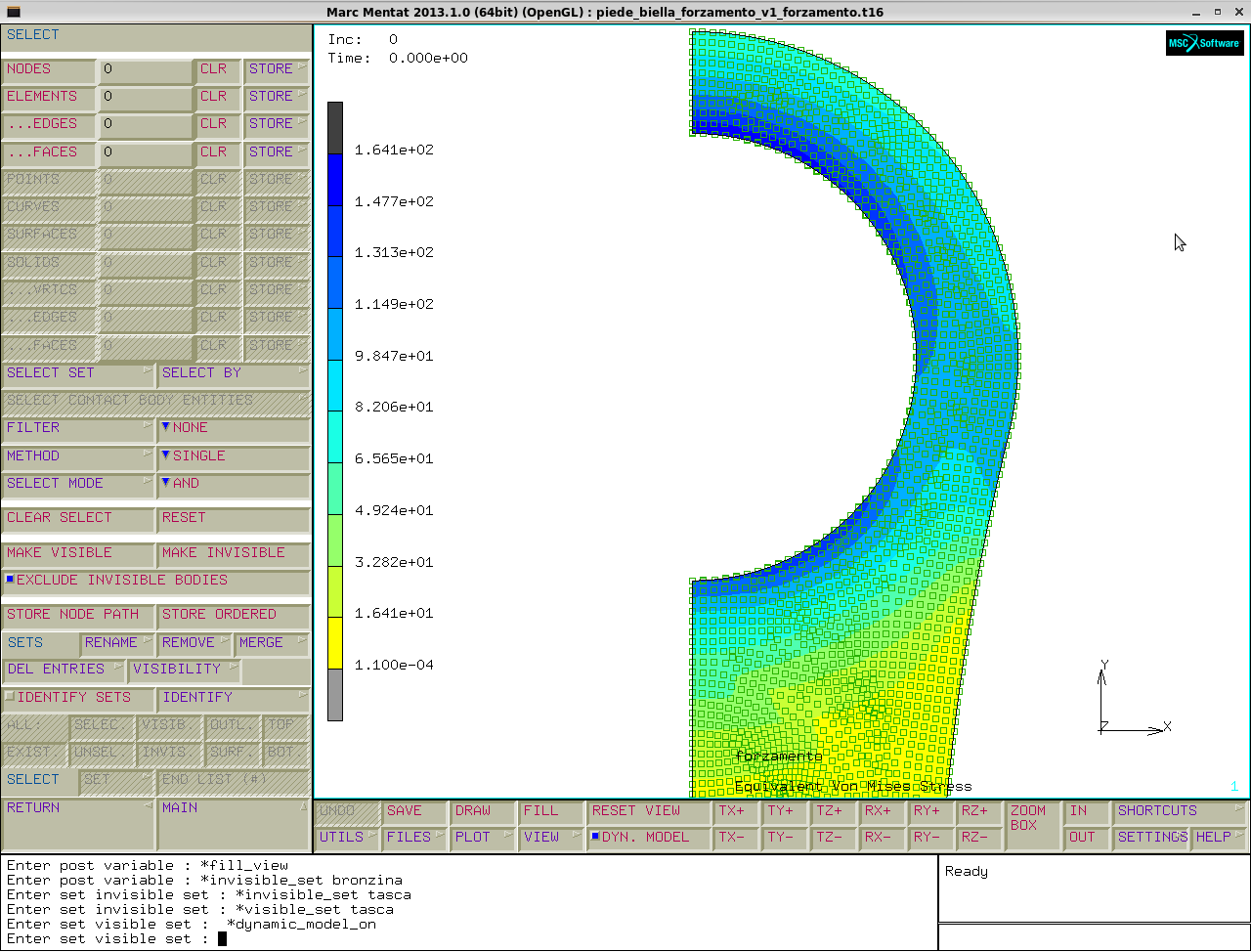
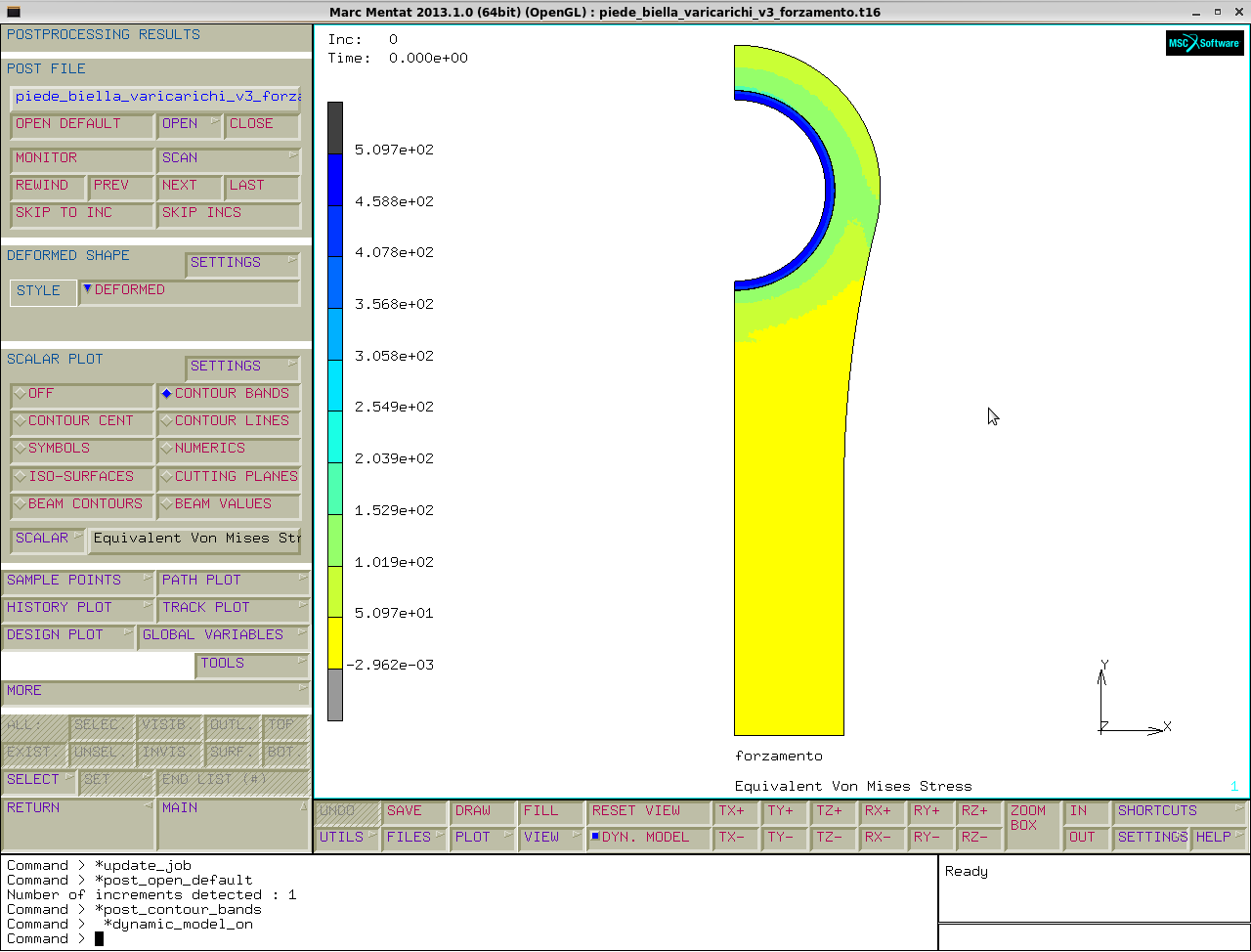
post file→select→visibility: disattiviamo la bronzina e guardiamo solo il piede.

Guardando l' equivalent von mises stress si vede che il forzamento non è una condizione di carico trascurabile in quanto raggiunge circa i 160 MPa.
Di fatto studiare il solo effetto del forzamento ha poco senso in quanto la biella è solita rompersi a causa dell' associazione del forzamento con cicli di lavoro.
Ci si chiede quando si ha un valore di forzamento sufficiente?
Se il forzamento fosse pari a 0, allora la bronzina non sarebbe solidale col piede, si avrebbe scorrimento e quindi usura.
Si ipotizzano due diverse condizioni per avere forzamento sufficiente:

• la bronzina non si deve staccare
• la bronzina non deve scorrere, altrimenti si avrebbe fretting fatigue.
  

FRETTING FATIGUE: può dare effetti positivi, nulli o negativi:

• lo scorrimento, quindi l' usura potrebbe eliminare le cricche che si formano in superficie (positivo)
• l' usura potrebbe favorire l' apertura delle cricche superficiali (negativo).
  

Quindi si può definire che il forzamento è sufficiente quando blocca la fretting fatigue.
Ora analizziamo e salviamo le forze nodali sull' interfaccia:
post processing→results→path plot (occorre definire il percorso)→node path: si clicca sul primo nodo del percorso e poi sugli altri a salti e infine sull' ultimo→end list.
Però il percorso sarebbe stato meglio farlo sul modello e non sui risultati, perchè in questi si ha tutto schiacciato sul piano z=0, quindi avrei 3 nodi sovrapposti.
menu→mesh generation→select→store node path→bordo interno piede: seleziono i punti come prima detto.
Rilancio il calcolo con il percorso rifatto.
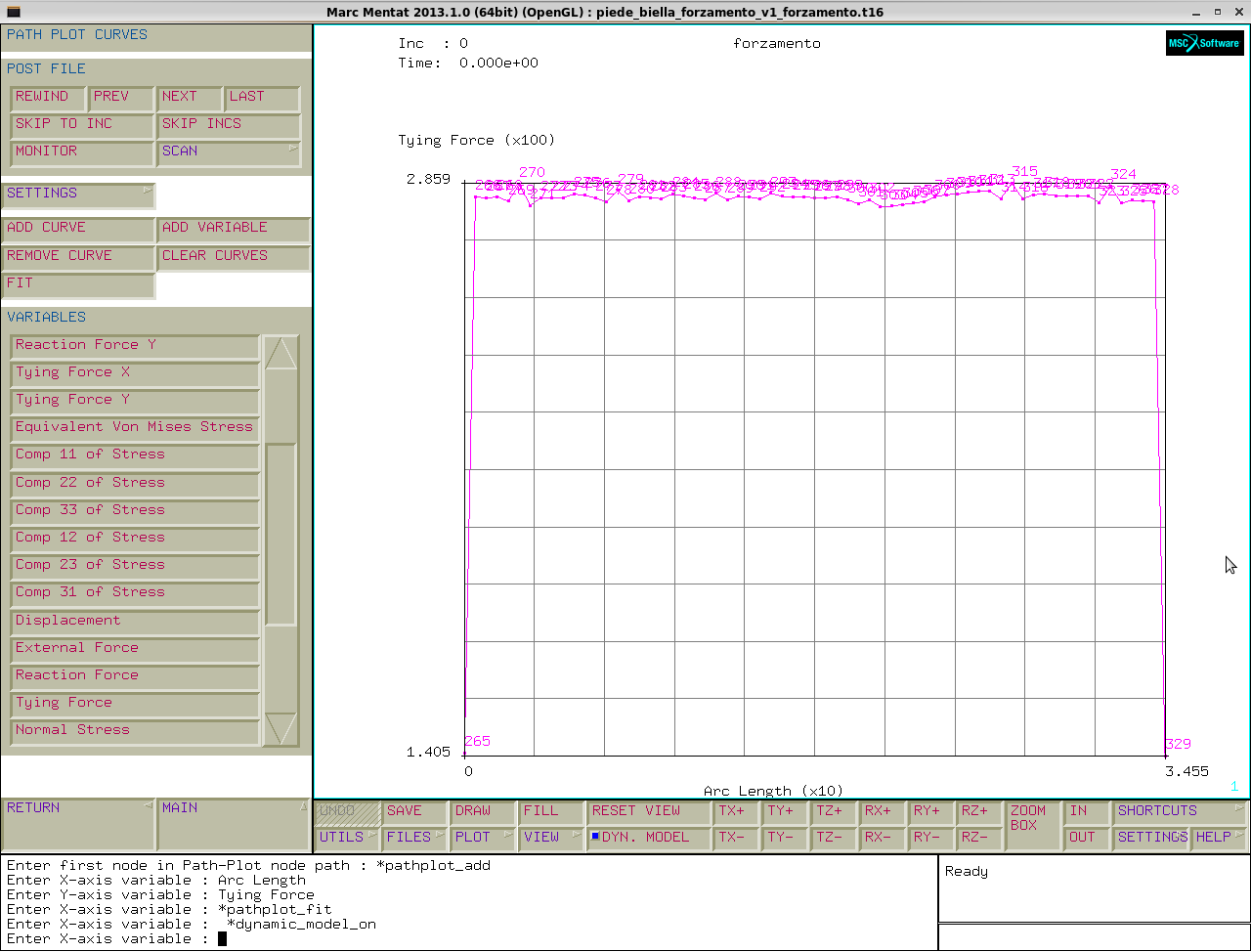
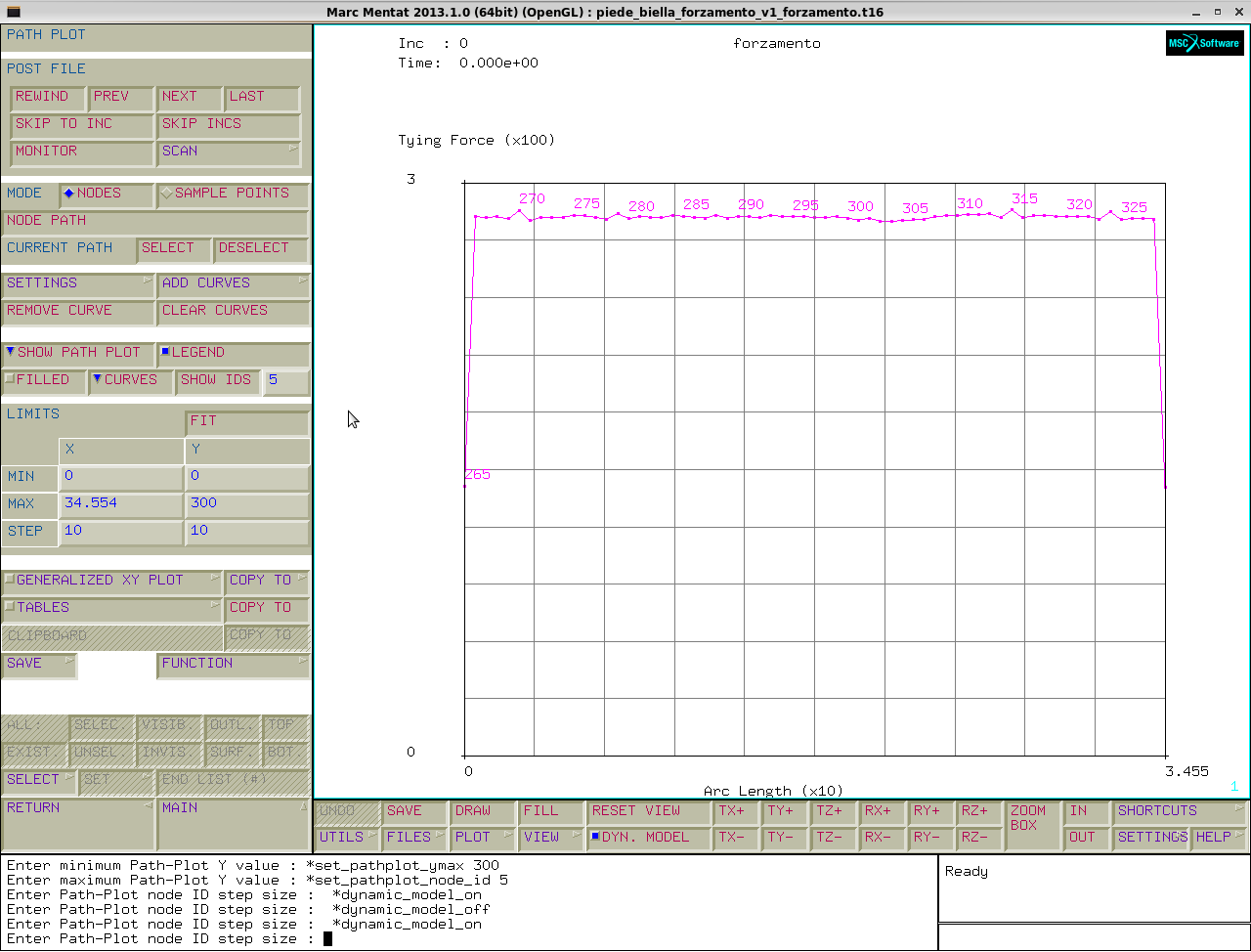
post file→path plot→node path→set→bordo interno piede→add curves→add curve→arc length (coordinata curvilinea x)→tying force (y)→fit→così otteniamo il grafico.

Mettiamo a posto la scala per visualizzare meglio.

Le forze dei legami sono circa la metà sui nodi esterni e praticamente costanti sul resto.
Le forze nodali uniformi, unite ad una mesh uniforme, permettono di ricavare una pressione di contatto uniforme.
Salviamo il grafico su un file di testo:
save→tying_forces_radiali_solo_forzamento.txt .

Ora dobbiamo creare le diverse condizioni di carico, cioè la TRAZIONE e la COMPRESSIONE.
La bibliografia ci fornisce due differenti forme per la pressione di contatto:

1. DEMIDOV-KOLKIN, $P_{max}=\frac{F}{2*r*S}$
2. GIOVANNOZZI, $P_{max}=\frac{3*F}{4*r*S}$
   

Per il caricamento trattivo si preferisce la prima, mentre per quello compressivo si preferisce la seconda.
Torniamo al modello e facciamo un job trattivo e uno compressivo.
Per fare ciò occorre prima cambiare le boundry conditions.
Prima ho imposto solo servo links sul g.d.l. radiale, mentre ora lo impongo anche sul g.d.l. tangenziale.
Copio il link 1→link 66→questo lo modifico mettendo il secondo g.d.l. : $V_{piede}=1*V_{bronzina}+1*V_{aux}$ .

mesh generation→duplicate→rotation→stesso passo di prima→repetitions:64 (1 in più di prima)→servos→scrivi “link 66”.
Rifaccio l' operazione di sweep per collassare i nodi duplicati.
A questo punto il modello contiene un conflitto di vincoli, allora rimuovo dal vincolo di simmetria i nodi problematici.
Inoltre dalla simmetria bisogna eliminare anche tutti i nodi che non sono nel piano di simmetria (errore commesso precedentemente, dovuto alla duplicazione).
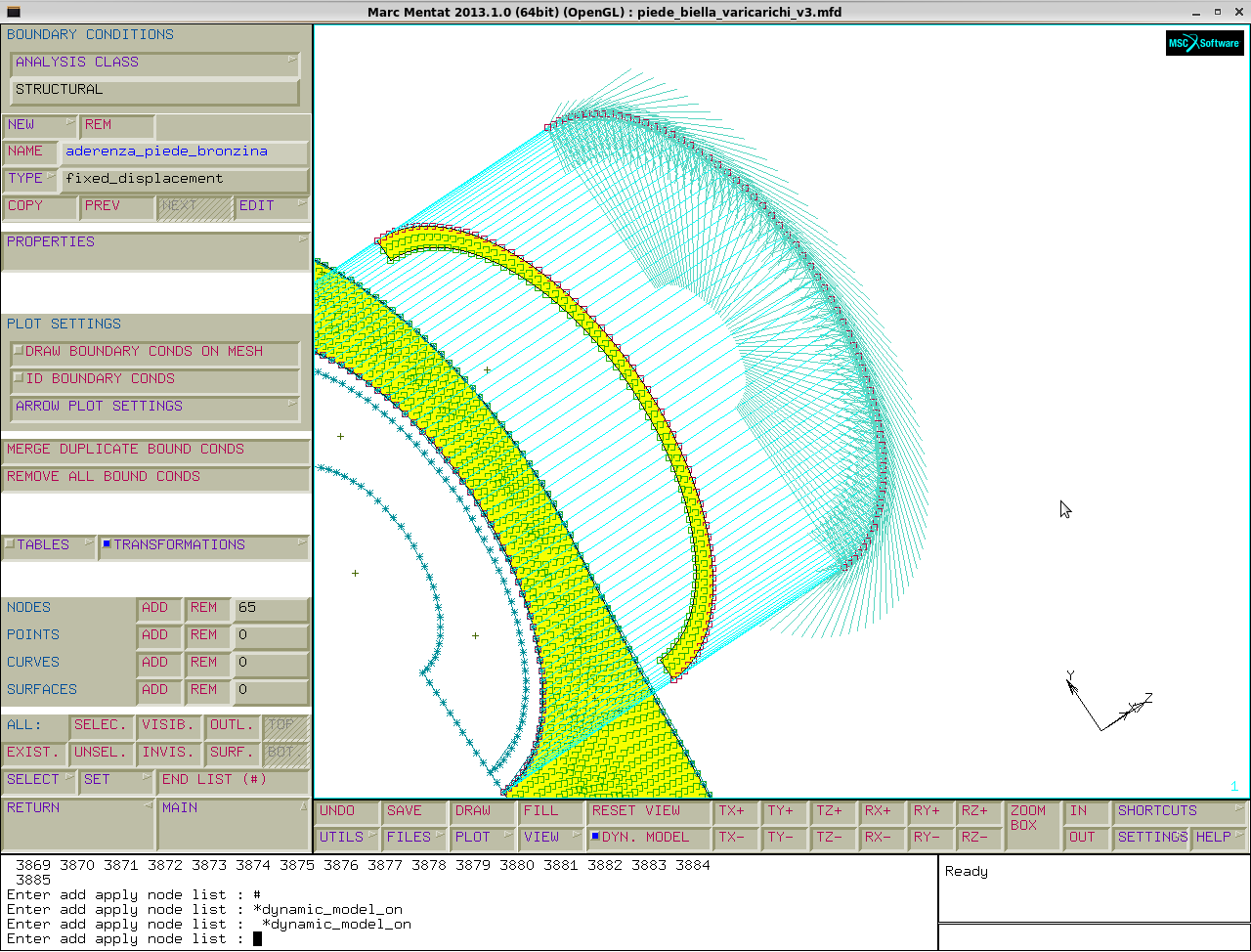
Creiamo una nuova boundry condition SPOSTAMENTO PIEDE=SPOSTAMENTO BRONZINA:
boundry conditions→new→name:ADERENZA_PIEDE_BRONZINA→fixed displacement→properties→displacement x=0 ; displacement y=0 →nodes→add→lo si applica ai nodi ausiliari.

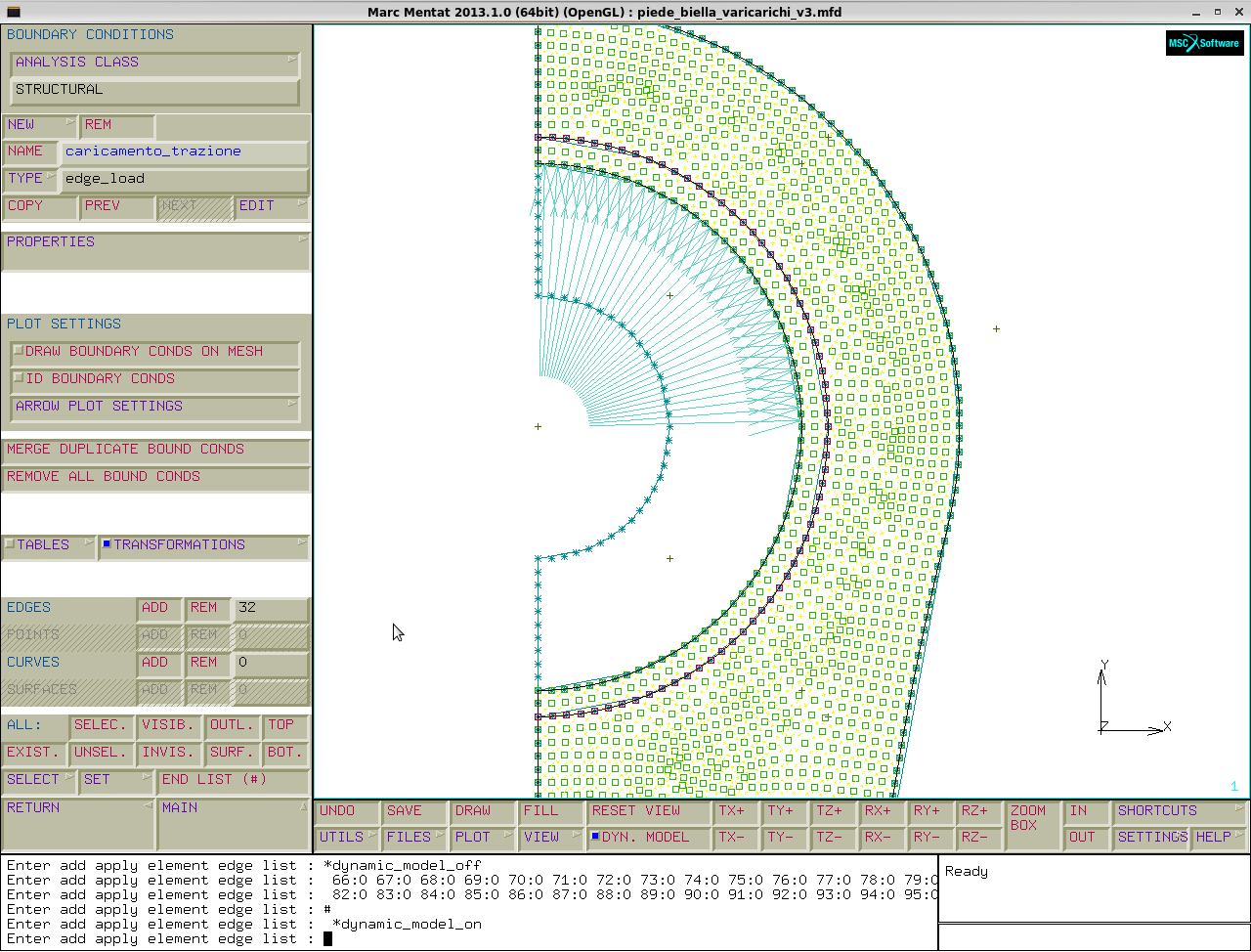
Ora si può procedere con il caricamento, ipotizziamo un carico trattivo (poi compressivo) di 10 KN:
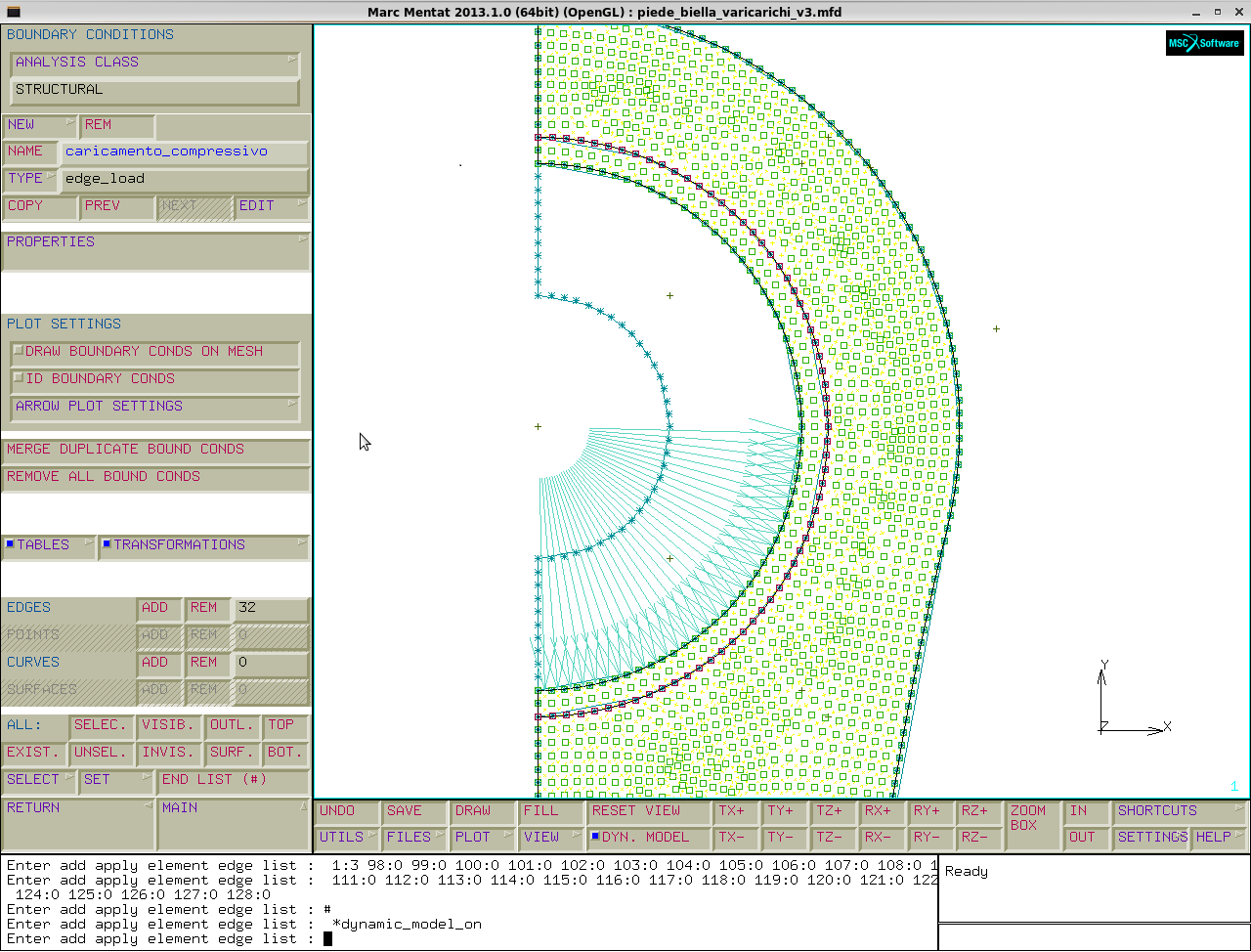
boundry conditions→new→name:CARICAMENTO_TRAZIONE→type→edge load→properties→edge load→pressure→41.66 MPa (calcolato con la formulazione Demidov-Kolkin)→edges add→selezioniamo 1/4 di interno biella.

Ora procediamo con il caricamento COMPRESSIVO.
Innanzitutto occorre creare una curva che vari con $\cos^2\theta$, come richiesto dalla formulazione del Giovannozzi:
tables→new→2 indipendent variables (x,y)→name: giova→V1→type:X0 coordinate(posizione del nodo sull' indeformata)→V2→type:Y0 coordinate.
Introduciamo la funzione ARCOTANGENTE2, la quale prende in input y e x e restituisce l' angolo.
→formula :cos(atan2(V2,V1)-Pi/2)^2.

boundry conditions→new→name: CARICAMENTO_COMPRESSIVO→type: edge load→properties→edge load→pressure→62.5 MPa→table→giova→edges→add→semiarco inferiore piede di biella.

Ora lanciamo i due calcoli:
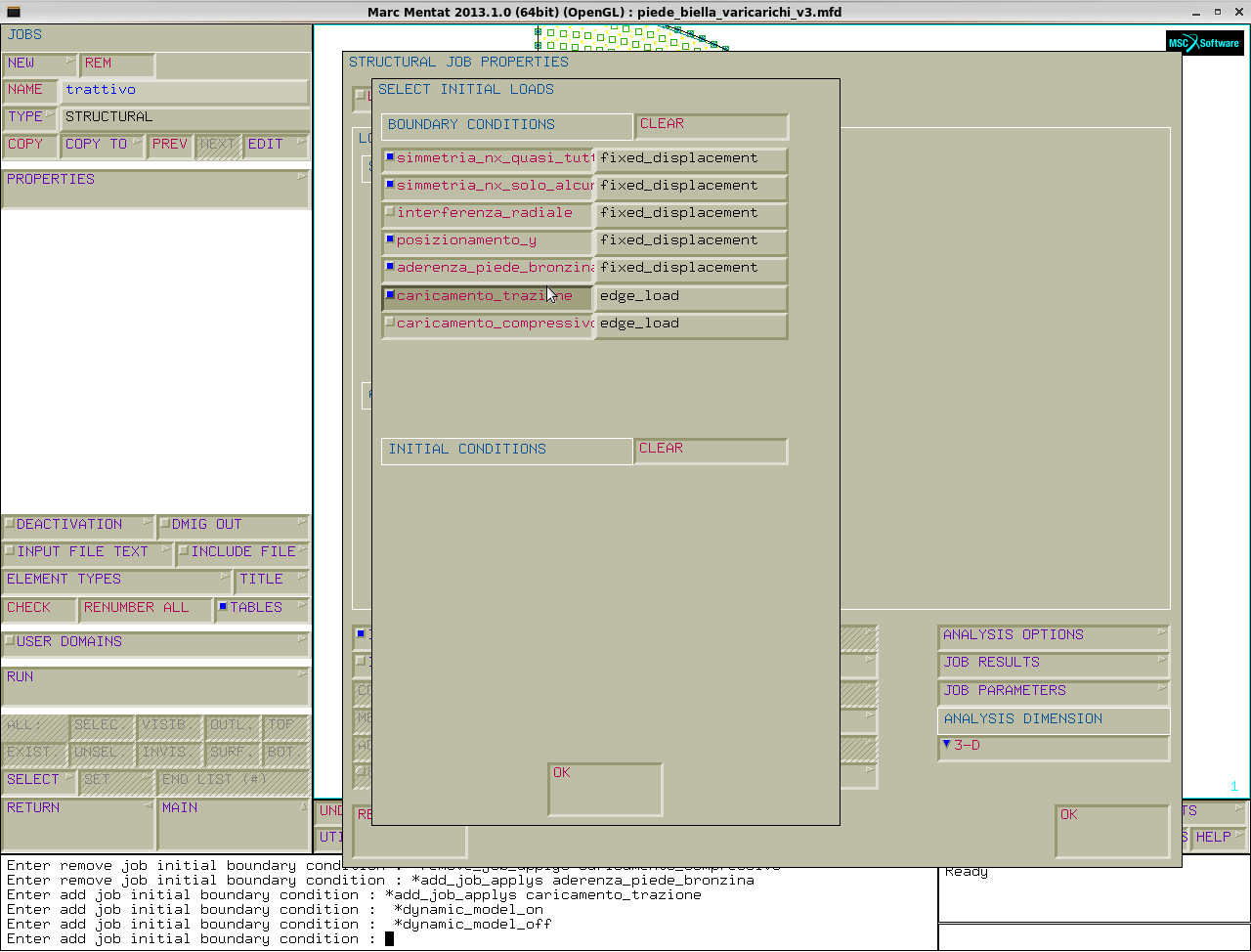
jobs→copy→name:trattivo→properties: disattivo interferenza radiale e caricamento compressivo.

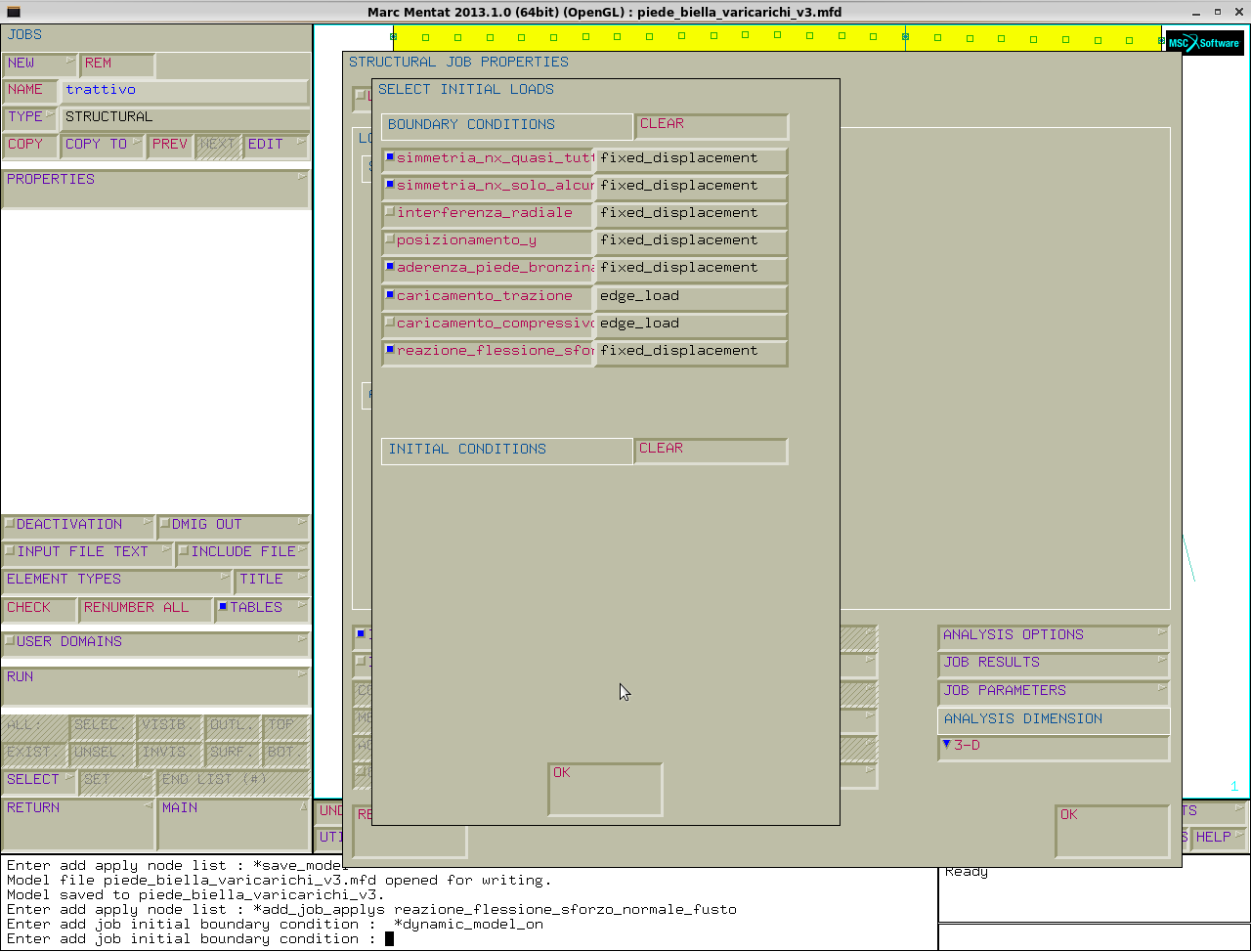
Però il caricamento trattivo non è autoequilibrato. allora disattiviamo il posizionamento y e creiamo una boundry condition che equilibri il carico:
boundry conditions→new→name: ipotesi_cinematica→fixed displacement→properties→displacement x=0→nodes→add: seleziono i nodi in basso→end list.

Ora rilancio il calcolo con questo initial load.

Lancio il calcolo anche nel caso compressivo adattando il caricamento.
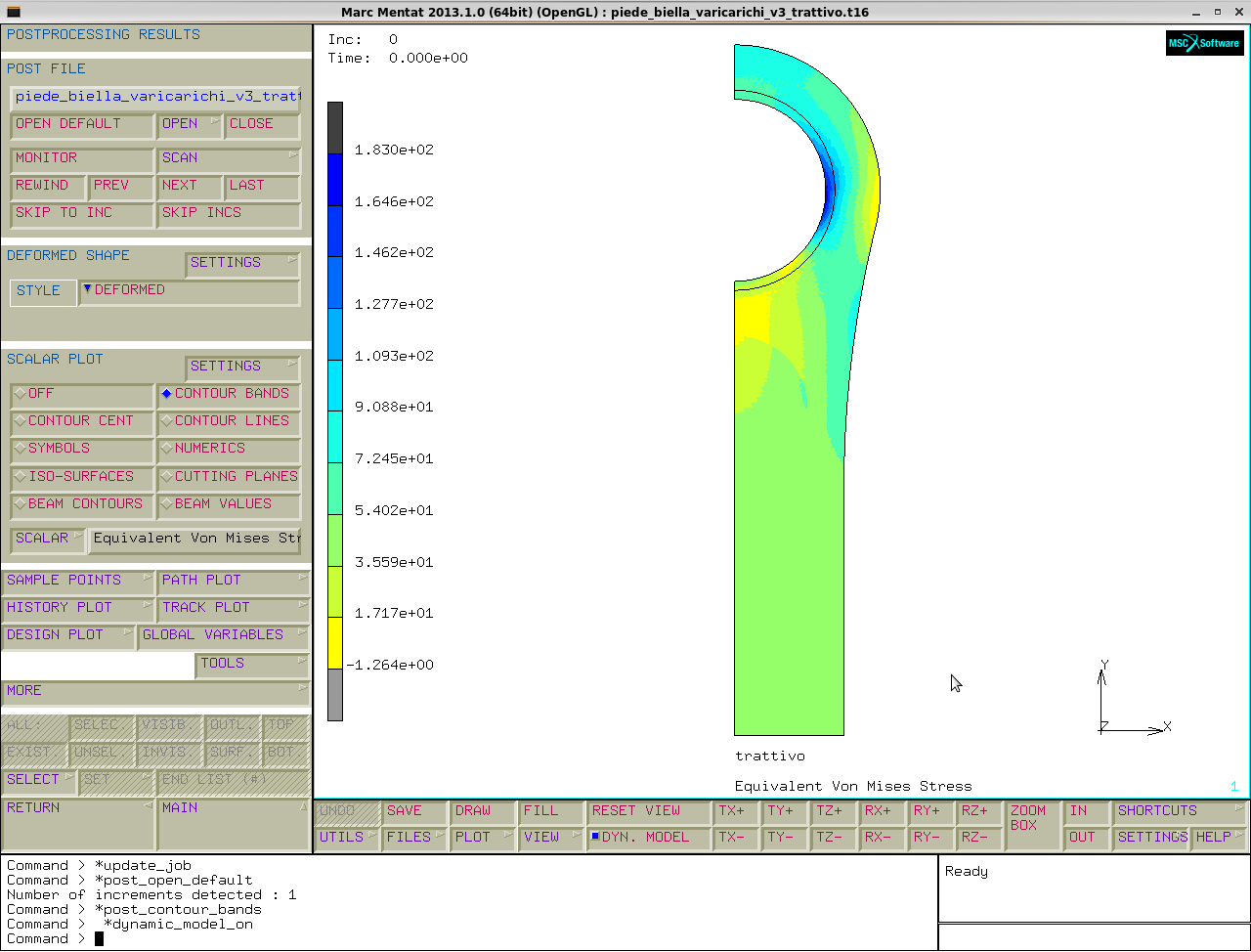
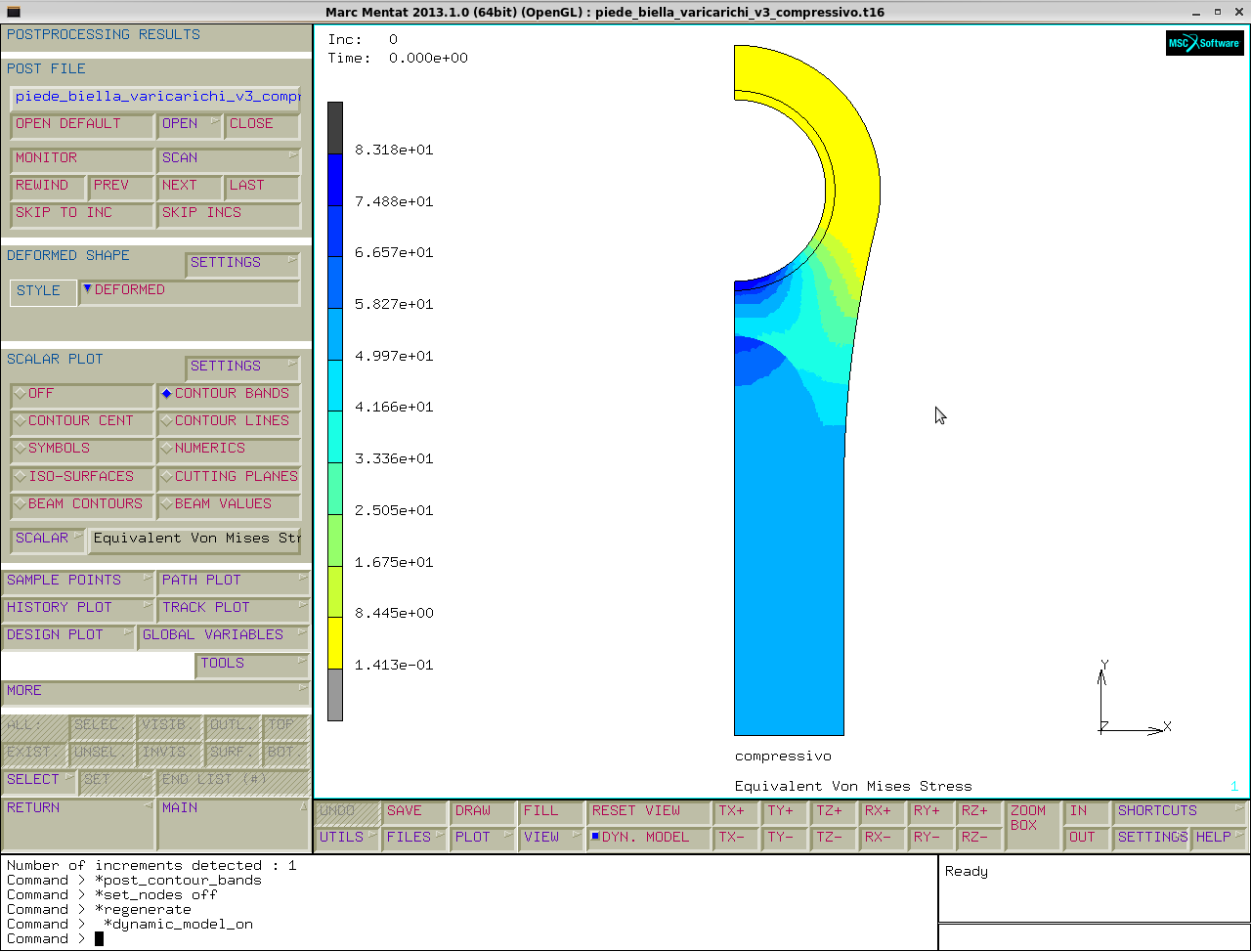
Otteniamo così le equivalent von mises stress per i tre casi: solo forzamento, trazione e compressione.

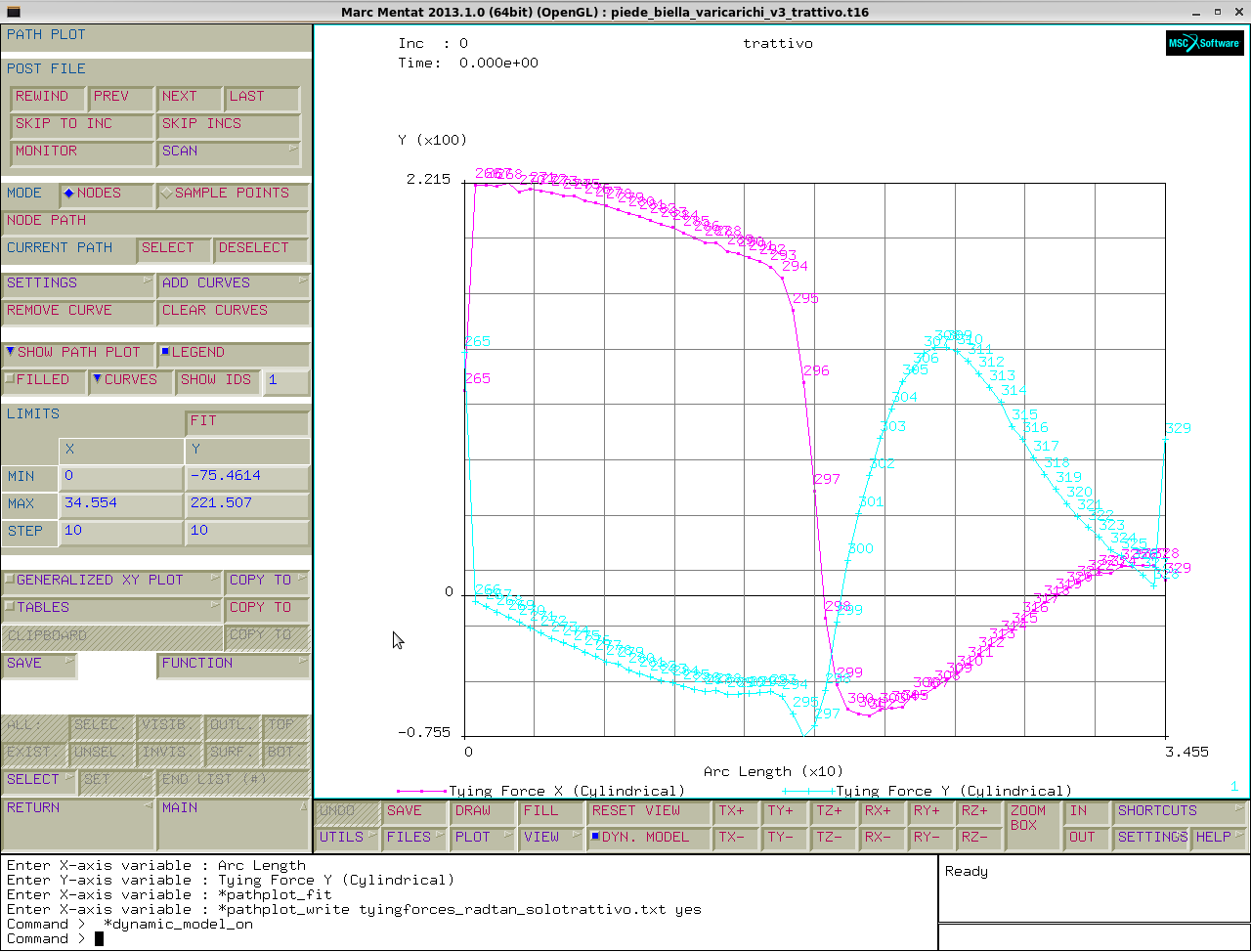
Infine guardiamo le forze all' interfaccia nel caso trattivo, scomponendole lungo x e lungo y:
trattivo→post file→original→scalar plot→results coordinate system→cylindrical→active.
Poi rigrafichiamo le tying forces rispetto all' arc length come fatto in precedenza.

Nella prossima lezione finiremo di analizzare i risultati ottenuti.

I motivi dell'open source

Intro FEM - da rileggere

code_aster_albero_fles_tors-1.pdf

seminario_code_aster_2015_albero_flex_tors.zip

albero_tors_nl.pdf

seminario_code_aster_2015_albero_flex_tors_nl.zip

seminario_code_aster_edf_08-advanced-nonlinear.pdf

login su cdm con estensioni grafiche:

ssh -X cdm

lancio salome su cdm:

salome

copia file con geometria su propria cartella home

cp /tmp/albero_d40_l40_d4_solo_geom.hdf ~/