Riprende dalla lezione precedente: Ho estratto modi propri e pulsazioni proprie del sistema, quindi abbiamo n coppie $w_i, x_i$, dove $w_i$ è la pulsazione propria, $x_i$ è il modo proprio associato.

In generale di queste ho una coppia per ogni grado di libertà del sistema.

Proprietà di questi modi propri:

Gli autovalori vengono definiti a meno di una costante arbitraria, tuttavia posso scegliere tra i tanti algoritmi di normalizzazione uno con significato fisico particolare

$$ \underline{\hat{x_i}}^T \underline{\underline{M}} \underline{\hat{x_i}} =1 \qquad\forall i $$

Mentre questa è una proprietà dimostrabile

$$ \underline{\hat{x_i}}^T \underline{\underline{M}}\underline{\hat{x_j}} =0 \qquad\forall i \neq j $$

Ho un’analoga proprietà associata alla matrice rigidezza, sempre per ogni i vale

$$ \underline{\hat{x_i}}^T \underline{\underline{K}}\underline{\hat{x_i}} = w_i ^2 $$ $$ \underline{\hat{x_i}}^T \underline{\underline{K}}\underline{\hat{x_j}} =0 $$ I modi propri sono ortogonali l’un l’altro, base massa e base rigidezza (proprietà non dimostrata), l’ortonormalizzazione rispetto alla massa fa si che rispetto alla rigidezza valga questa condizione per cui $$ \underline{\hat{x_i}}^T \underline{\underline{K}}\underline{\hat{x_i}} = w_i ^2 $$ dove $w_i$ è la pulsazione propria. Questo sempre se il modo proprio è normalizzato a massa modale unitaria.

Queste proprietà possono essere utili per il problema della risposta in frequenza: io avevo una forma algebrica

$$ (-w^2 \underline{\underline{M}} +jw \underline{\underline{C}} + \underline{\underline{K}} )\underline{\bar{x}}= \underline{\bar{f}} $$

Questo vettore contiene, per ogni grado di libertà la quota reale e immaginaria della forza esterna applicata, o modulo e facce della forza esterna applicata.

$$ \underline{f} (t) = Re (\underline{\bar{f}} e^{jwt}) $$

$$ \underline{x} (t) = Re (\underline{\bar{x}} e^{jwt}) $$

Questo tipo di gradi di libertà implica che noi descriviamo la deformazione della struttura per sommatoria pesata di forme di spostamento in cui si muove un solo grado di libertà, ossia $\bar{x} $ (configurazione della struttura) posso immaginarlo come somma di forme di moto elementari( es: sul primo grado di libertà si sposta il valore 1 e tutti gli altri sono fermi, moltiplicato per $\bar{x_1}$, ossia questa forma di moto è considerata, poi come peso la prima componente di questo vettore più una forma di moto diversa pesata per la seconda componente del vettore, …)

$$ \underline{\bar{x}} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ \vdots \end{pmatrix} \bar{x_1} + \begin{pmatrix} 0 \\ 1 \\ 0 \\ \vdots \end{pmatrix} \bar{x_2} + ... $$

Questo è un modo per rappresentare, variare arbitrariamente queste componenti in modo da rappresentare tutte le possibili configurazioni della struttura, non è l'unico. In geometria diremmo che lo spazio delle possibili configurazioni è lo spazio $\mathbb{R}^n $ dove n è il numero di gradi di libertà, dove il vettore (1 0 0 0 …) è una base di quello spazio vettoriale, non è però l'unica base, avrei $\infty^1 $ basi, questa è la base più comoda, ma ha proprietà poco interessanti per la nostra analisi. Immagino di usare una base diversa per $\mathbb{R}^n $, in particolare una base di $\mathbb{R}^n $ è una qualsiasi n-upla di vettori linearmente indipendenti rispetto agli altri. Ora so che gli autovettori sono tutti indipendenti l'un l'altro e sono proprio n.

$\bar{x_i}$ è la base per i = 1,…,n; devono essere linearmente indipendenti , posso usarli per costruire la base. Ora scrivo la mia generica configurazione non come somma associata alla base naturale, ma come somma di contributi

$$ \underline{\bar{x}} \in\mathbb{R}^n $$

$$ \underline{\bar{x}} = \begin{vmatrix} \vdots\\ {\hat{x_1}}\\ \vdots \end{vmatrix} \zeta_1 + \begin{vmatrix} \vdots\\ {\hat{x_2}}\\ \vdots \end{vmatrix} \zeta_2 + ... + \begin{vmatrix} \vdots\\ {\hat{x_n}}\\ \vdots \end{vmatrix} \zeta_n $$

L'ultimo termine mi costringerebbe a calcolare tutti i modi propri della struttura che diventa difficile nel continuo. Se uso tutti gli autovettori ho una base per $\mathbb{R}^n $, se non riesco a ricavarli tutti mi fermo ad un certo m (m $\leq$ n); se uso tutti i modi propri del sistema, variando i parametri, a ricoprire l'intero sistema $\mathbb{R}^n $ delle possibili configurazioni va bene, se ne uso un sottoinsieme non riesco a coprire tutto $\mathbb{R}^n $, ma copro solo un sottoinsieme di $\mathbb{R}^n $. Se il sottoinsieme contiene tutto ciò che è ingegneristicamente rilevante allora va bene, altrimenti dovrò ampliare, è possibile scrivere una possibile configurazione invece che per composizione di elementi della base naturale, per composizione degli elementi di una base costruita a partire da tutti o alcuni degli autovettori.

Nota bene: se ne prendo solo alcuni non posso più spaziare tutto $\mathbb{R}^n $, ma mi limito ad un sottoinsieme delle possibili configurazioni.

Quindi posso scrivere questo oggetto in forma compatta costruendo una matrice in cui raccolgo per colonne gli autovettori:

$$ \newcommand{\mat}[1]{\smash{\underline{\underline{#1}}}} \underline{\bar{x}} = \underbrace{ \begin{bmatrix} \vdots & \vdots & \cdots & \vdots \\ \hat{x_1} & \hat{x_2} & \cdots & \hat{x_m} \\ \vdots & \vdots & \cdots & \vdots \\ \end{bmatrix}}_{\mat{\hat{X}}} \newcommand{\mat}[1]{\smash{\underline{#1}}} \underbrace{ \begin{bmatrix} \xi_1\\ \xi_2\\ \vdots\\ \xi_m \end{bmatrix}}_{\mat{\bar{\xi}}} \qquad(1) $$

La matrice $ \underline{\underline{\bar{X}}}$ ha n righe ed m colonne ed il vettore $\underline{\bar{\xi}}$ ha n elementi; quindi posso scrivere: $ \underline{\bar{x}} = \underline{\underline{{\hat{X}}} }\underline{\bar{\xi}} $

Questa equazione può essere utilizzata nell’equazione algebrica di equilibrio, infatti inserendo $\underline{\bar{x}}$ ottenamo n equazioni di equilibrio in m incognite:

$$ \newcommand{\mat}[1]{\smash{\underline{#1}}} (- \omega^2 \underline{\underline{M}} + j\omega\underline{\underline{C}} + \underline{\underline{K}}) \underbrace{\underline{\underline{\hat{X}}} \underline{\bar{\xi}}}_{\mat{\bar{x}}} = \underline{\bar{f}} $$

Premoltiplicando $\underline{\underline{\hat{X}}}^T$, ottengo :

$$ \underline{\underline{\hat{X}}}^T (- \omega^2 \underline{\underline{M}} + j\omega\underline{\underline{C}} + \underline{\underline{K}})\underline{\underline{{\hat{X}}} }\underline{\bar{\xi}} = \underline{\underline{\hat{X}}}^T \underline{\bar{f}} $$

A questo punto posso scrivere:

$$ \newcommand{\mat}[1]{\smash{#1}} (-\omega^2 \underbrace{\underline{\underline{\hat{X}}}^T \underline{\underline{M}}\underline{\underline{\hat{X}}} }_{\mat{I}} + \newcommand{\mat}[1]{\smash{#1}} j \omega \underbrace{\underline{\underline{\hat{X}}}^T \underline{\underline{C}}\underline{\underline{\hat{X}}} }_{\mat{II}} + \newcommand{\mat}[1]{\smash{#1}} \underbrace{\underline{\underline{\hat{X}}}^T \underline{\underline{K}}\underline{\underline{\hat{X}}} }_{\mat{III}}) \underline{\bar{\xi}} = \underline{\bar{q}} \qquad(2) $$

Per le proprietà di ortogonalità, citate precedentemente, si ha che:

I

La $\underline{\underline{\hat{X}}}^T$ è una matrice riempita dagli autovalori per riga; infatti il termine segnato in rosso è uguale all’i-esimo autovettore del sistema, che sarebbe l’i-esima riga della matrice $\underline{\underline{\hat{X}}}^T$, moltiplicato per la matrice massa $\underline{\underline{M}}$ e per la j-esima colonna della matrice $\underline{\underline{\hat{X}}}^T$; ovvero:

$\underline{\hat{x_i}}^T \underline{\underline{M}} \underline{\hat{x_j}} = \delta_{ij}$

In particolare questa matrice ha termini non nulli quando i=j ,ovvero sulla diagonale principale, mentre vale 0 se i e j sono diversi. Quindi questa matrice risulta uguale alla matrice identità:

$\underline{\underline{\hat{X}}}^T = \underline{\underline{I}}$

II

Questo caso è simile al precedente, l’unica differenza è che il delta di Kroneker ($\delta_{ij}$) è moltiplicato per $\omega_(i)^2$:

$\underline{\hat{x_i}}^T \underline{\underline{K}} \underline{\hat{x_j}} = \delta_{ij} {\omega_{i}}^2$

In questo caso non ho una matrice identità ma ho una matrice diagonale della quale i termini diagonali sono le varie pulsazioni proprie:

Questa matrice la possiamo chiamare matrice $\Lambda$.

III

Per la MATRICE SMORZAMENTO non possiamo fare le precedenti considerazioni in quanto quest’ultima è una matrice non diagonale e bandata. Se questa matrice fosse diagonale il sistema (2) sarebbe un sistema in cui si avrebbe la somma dei tre contributi delle matrici diagonali, ovvero sarebbe un sistema a matrice diagonale. Un sistema a matrice diagonale ha la proprietà di non essere un sistema ma solo delle equazioni (nel nostro caso sarebbero 3) che si potrebbero risolvere l’una indipendentemente dall’altra, e quindi ha un costo computazionale molto basso.

Per sopperire a questo problema suppongo che $\underline{\underline{C}}$ risulti diagonale, ovvero impongo l’IPOTESI DI RAYLEIGH per cui:

$\underline{\underline{C}} = \alpha \underline{\underline{M}} + \beta \underline{\underline{K}} \qquad (3)$

Supponendo di poter ridurre lo smorzamento nella forma (3), ottengo ch il sistema (2) sotto le ipotesi di Rayleigh risulta diagonale: $$ \underline{\underline{\hat{X}}}^T \underline{\underline{C}} \underline{\underline{\hat{X}}} = \alpha \underline{\underline{I}} + \beta \underline{\underline{\Lambda}} $$

Così facendo ottengo un sistema:

$$ (-\omega^2 \underline{\underline{\hat{X}}}^T \underline{\underline{M}}\underline{\underline{\hat{X}}} + j \omega \alpha \underline{\underline{I}} + \beta \underline{\underline{\Lambda}} + \underline{\underline{\Lambda}}) \underline{\bar{\xi}} = \underline{\bar{q}} \qquad(4) $$

La matrice del sistema è diagonale, per cui posso scomporre il sistema (4) nelle equazioni indipendenti di cui è costituito. La sigola equazione risulta ($\forall i = 1, \dots , m$):

$$ (-\omega^2 \underline{\underline{I}} + j\alpha\omega + j\beta{\omega_i}^2\omega +{\omega_i}^2)\bar{\xi_i} = \bar{q_i} \qquad(5) $$

con: $\omega ^2$ : pulsazione della forzante

${\omega_i}^2$ : pulsazione propria, presa dalla matrice $\underline{\underline{\Lambda}}$

la (5) si risolve dicendo che :

$$ \bar{\xi_i} = \frac{\bar{q_i}}{(-\omega^2 + j\alpha\omega + j\beta{\omega_i}^2\omega +{\omega_i}^2)} $$ Quindi passo da un sistema da n equazioni in n incognite, ad n equazioni ed m incognite ad m dicisioni che non sono più un sistema.

In realtà mi accorgo che da questa equazione posso ricostruire l'equazione dinamica iniziale, infatti l' equazione precedente risulta essere la forma algebrica associata all'equazione:

$$ \ddot{\xi} + 2\omega_i (\frac{\alpha}{\omega_i}+\beta \omega_i) \dot{\xi} + {\omega_i} ^2 \xi = \bar{q}_i e^{j\omega t} $$

Se si prende un oscillatore ad 1 gdl ($\xi_i$), con massa unitaria, in cui lo smorzamento chiamato $\zeta_i$ forzato dalla forzante ($q_i e^{jwt}$), si ottiene dalla formula precedente. La soluzione di ognuna delle equazioni di cui si compone il sistema diagonalizzato può essere vista come associata ad un oscillatore ad 1 gdl. Mediante la diagonalizzazione del sistema arrivo a definire concettualmente m oscillatori a 1 gdl che si possono considerare indipendentemente l'uno dall'altro. $\zeta_i$ non è lo smorzamento dimensionale, ma è lo smorzamento frazione del critico, per cui quando: $\zeta_i$ = 0, la soluzione è di tipo periodico, quando $\zeta_i$ è piccolo si ha una soluzione di tipo oscillante di tipo periodico che però non perdura per ogni valore di smorzamento. Esiste un valore di smorzamento critico oltre il quale non esiste una soluzione periodica, ma un lento tendere ad una soluzione statica.

Scrivendo $\zeta_i$ = $\zeta_i e^{jwt}$ escludo di essere in condizione critica, quindi assumo di essere in condizione subcritica e quindi con smorzamento piccolo, in particolare perdo l'andamento armonico della soluzione per il valore di smorzamento $\zeta_i$ =1, motivo per cui deve essere $\zeta_i$ <1, ed è defino come frazione del valore critico a cui perdo la soluzione armonica del sistema.

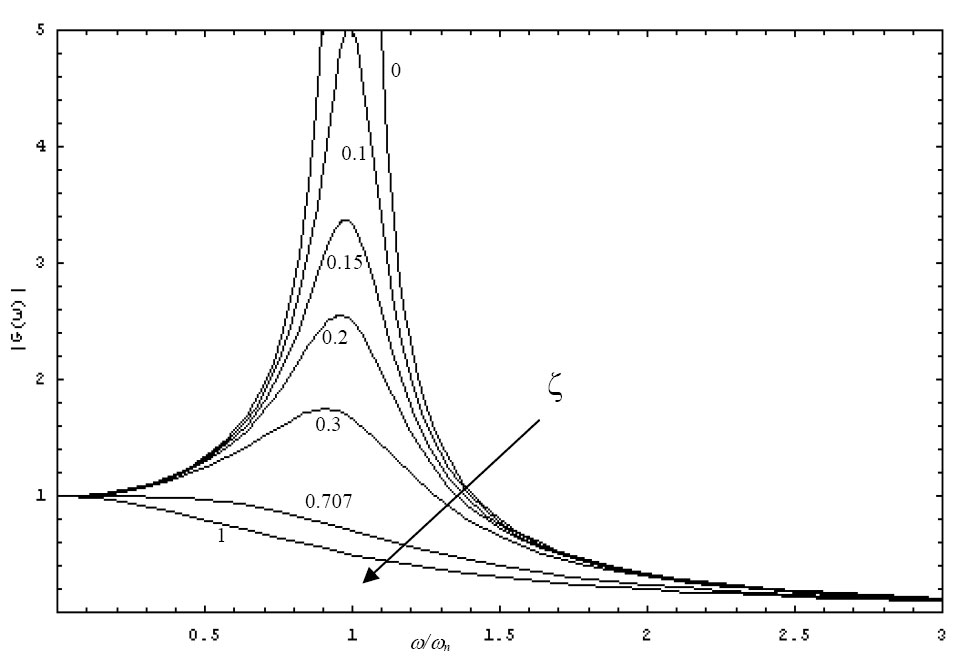
In questo diagramma è riportata una tipica funzione di risposta dell'oscillatore, e contiene più o meno tutte le possibili soluzioni.

Sull'asse x vi è il rapporto tra la (frequenza di eccitazione/frequenza propria), nel nostro caso si moltiplica tutto per $\pi_i$ e si ottiene il rapporto tra eccitante/i-esima pulsazione propria. Come asse y si ha XK/$F_0$, nel nostro caso

X = |$\xi_i$| che può essere complesso quindi prendo il modulo;

K = $\omega^2_i$ (in un oscillatore monodimensionale è la rigidezza)

$F_0$ = |$q_i$| modulo della forzante.

Nota la forzante e la pulsazione critica per ogni modo proprio, mi posiziono sull'asse x, noto o smorzamento $\zeta_i$ <1, (non si hanno informazioni per $\zeta_i$ >1 perchè la risposta non è periodica) riesco a ricavare $\xi_i$ da grafico ed ho la soluzione, ricavo il modulo |$\xi_i$| , e poi ricavo la fase.

Per ogni oscillatore trovo $\xi_i$ che è soluzione del problema. Questo deve essere moltiplicato per l'autovettore associato $x_i$ , e la somma dei contributi per ognuno dei modi propri considerati fornisce la risposta del sistema globale.

In conclusione dopo aver scomposto il sistema a n gdl in m oscillatori indipendenti, risolvo ogni oscillatore e poi ricompongo i risultati per avere la risposta del sistema globale. Questa procedure si chiama: ANALISI DI RISPOSTA PER SOVRAPPOSIZIONE MODALE.

Consideriamo per chiarezza un diapason, costruito in acciaio a bassissimo smorzamento strutturale. I modi propri, sono vari, ma uno dei possibili, consiste nella contro oscillazione dei bracci, ossia apertura e chiusura degli stessi in maniera simmetrica, solitamente tale moto si considera ad una frequenza di 440 Hz. Si consideri di ricercare la risposta del sistema ad una forza oscillate, parallela al suolo, applicata all'estremità superiore del braccio sinistro, diretta da sinistra a destra(diapason incernierato al suolo con bracci disposti disposti verticalmente), forza del tipo F=Re(e^jωt).

Al moto proprio considerato, risulta essere l'i-esimo (non sarà il più piccolo, conicidente con il moto smorzato),è associato lo smorzamento, ζi, molto basso, (ζi«1), tale da poterlo considerare uguale a zero, mediante approssimazione tollerabile. Si ci chiede, come si comporti il sistema diapason, con eccitamento modulato con forzante ω, uguale ad ωi, dunque pulsazione propria. Come evidente dal grafico, per smorzamento nullo, la risposta tenderà ad assumere valore infinito. Ciò accade perché, il picco del grafico, per piccoli smorzamenti, ho valore pari a 1/2 ζi. La condizione in analisi, viene detta condizione di risonanza, cioè eccitante pari alla pulsazione propria del sistema. Il problema così impostato, avrà come soluzione la somma di tanti moti propri, di cui uno, coincidente con la risonanza, che sarà il moto proprio moltiplicato per infinito. Tale moto, avrà oscillazione sempre crescente nel tempo, tendente appunto, ad infinito. La presenza della condizione di risonanza, rende trascurabili gli altri moti propri presenti. Se la forzante, assume un valore pari alla metà della più piccola frequenza critica, posizionandoci sul grafico della risposta, si può verificare, che mediante calcolo statico, si sottostima di un valore compreso tra radice di due e uno, la risposta del primo moto proprio, per tutti gli altri si avrà un errore inferiore; dunque dal rapporto tra la pulsazione eccitante e la più bassa delle pulsazioni proprie, si può verificare l'accuratezza, della soluzione puramente statica. In definitiva, si può affermare che l'utilità dell'analisi modale, è verificare la necessità di una analisi dinamica, o se in alternativa, sia sufficiente la trattazione statica. Ciò mediante l'output di una pulsazione caratteristica, da confrontare con le pulsazioni proprie, in particolare della prima che è in grado di eccitare il sistema. ( se la prima pulsazione propria è molto maggiore della pulsazione propria della forzante, si può effettuare una analisi statica). La validità dell'approssimazione del sistema a statico, è soggetta ad una soglia di errore, verificabile dal grafico della risposta in frequenza. Il fatto di considerare smorzamento nullo risulta di interesse ( ζi, solitamente non è inferiore al millesimo, per acciai armonici),puramente teorico, in quanto ζi, si compone non solo dell'effetto dato dal materiale, ma è somma di contributi dovuti a giunti o collanti di fissaggio, oltre che dal mezzo (fluido, di cui va considerata la massa messa in movimento) entro il quale avvengono le oscillazioni.

Tutte queste considerazioni le abbiamo fatte con una matrice nella forma di Rayleigh. Lo smorzamento nella forma di Rayleigh è una matrice che è rappresentata dalla composizione di due matrici, una di massa e una di rigidezza.

C = αM + βK

Dove le costanti α e β hanno unità sec^{-1} and sec rispettivamente. Per entrambe queste matrici di smorzamento, la matrice C è diagonale grazie all’ortogonalità dei modi: matrice di sistemi classicamente smorzati.

Se parlo di smorzamento strutturale mi va molto bene perché è proporzionale alla rigidezza. Viene naturale costruire una matrice di smorzamento come scalatura della matrice di rigidezza, perché il materiale che da una reazione elastica con leggero ritardo in modo implicito, ha un giro di isteresi e un ciclo di dissipazione. Risulta naturale definire questo coefficiente β nel caso che lo smorzamento sia di tipo strutturale dato che si riesce a ricavare ζ in funzione dello smorzamento naturale.

la matrice massa è una matrice definita positiva, che a fronte di un moto di corpo rigido ha una reazione inerziale , se ho $$\alpha \neq 0$$ ho una razione di tipo viscoso.

In assenza di smorzatori collegato a terra, cioè potrebbe essere l’area attorno a un corpo è uno smorzatore che lega il corpo con qualcosa di remoto fermo che dissipa energia. Esempio uno smorzatore legato a due punti a fronte di un corpo rigido della struttura non agisce. Nel caso abbia solo smorzatori tra punti della smorzatura farei in modo che questo $$\alpha = 0$$, se sono interni alla struttura questi punti non si ha smorzamento.

dalla matrice di smorzamento risulta:

$$ \bigl(\begin{smallmatrix} .& .& .& .& .\\ .& c& .& -c& .\\ .& .& 0& .& .\\ .& -c& .& c& .\\ .& .& .& .& . \end{smallmatrix}\bigr)$$

Se prendo la matrice di smorzamento rispetto alle due braccia del diapason , ho una matrice con 4 elementi non nulli. E' molto difficile rappresentare in forma di Rayleigh, matrice completamente piene senza nessun elemento nullo dato che è considerata come composizione di due matrici m e k. lo smorzamento in forma di Rayleigh è molto comodo. Se ho elementi smorzati concentrati conviene non usare questa forma ma analizzare la risposta del sistema semplicemente utilizzando il sistema algebrico da cui siamo partiti eseguendo una semplificazione della matrice di smorzamento dato che lo smorzamento è proporzionale alla rigidezza.

Per il calcolo dello smorzamento non si è ancora risolto allora possiamo adoperare due strade:

1- Prove sperimentali su telai vecchi. 2- Definire l'ampiezza della risposta con valori a caso , cioè scegliere in modo arbitrario i valori di z piccoli.

Si consiglia ζ piccoli per armonizzare la risposta, tale per cui facendo un confronto grafico fra ζ 0,1 centesimo è ζ valore nullo avrei un errore del 20%.

Per ζ nullo avrei ampiezze maggiori e un eccesso di risposta ed è un sistema conservativo, dato che non è definito lo smorzamento, dal momento che devo astenermi nel portare qualunque valore a risonanza e con diversi metodi numerici migliorare i risultati di smorzamento a valori crescenti.

Il moto di corpo rigido diventano modi propri a Hz nulla con il metodo fi Rayleigh.

Indicazioni damping ratio di riferimento:

https://engineering.purdue.edu/~ce573/Documents/Structural%20damping%20values_JDStevenson.pdf

http://iopscience.iop.org/1742-6596/268/1/012022/pdf/1742-6596_268_1_012022.pdf

http://teaching.ust.hk/~mech300/mech300_7_1_damping_ref.pdf

http://www.vibrationdata.com/tutorials/bolted_joint_damping.pdf