La prima parte della lezione è stata incentrata sull'impostazione del calcolo con Maxima delle caratteristiche di sollecitazione su una testa di biella.

N.B: Questo è uno degli esercizi da svolgere in vista dell'esame finale

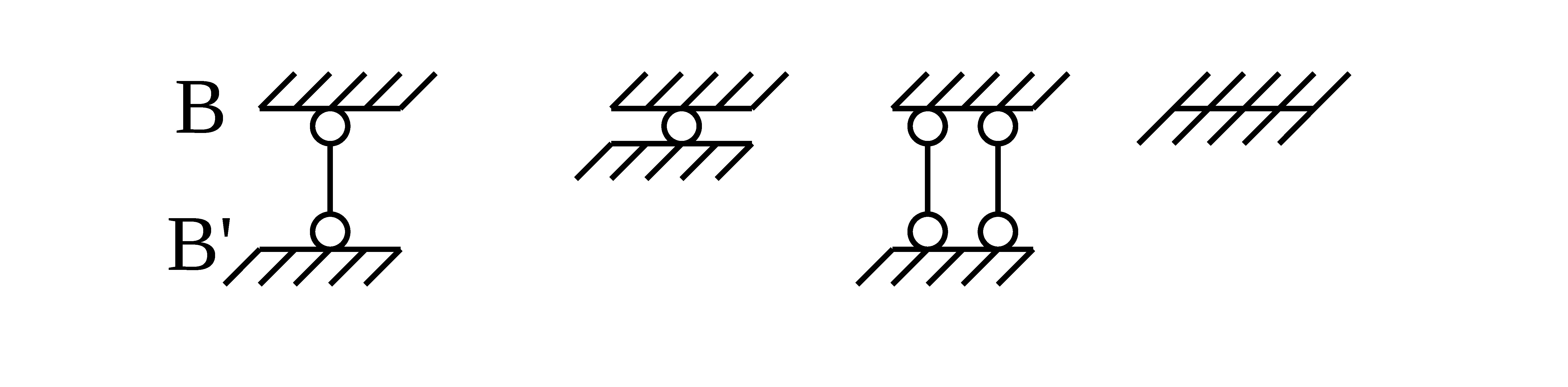
La testa della biella è formata da un cappello che viene imbullonato sul fusto; in questo esercizio, il collegamento tra il punto terminale del cappello (B) e l'estremo del fusto (B') deve essere simulato in uno dei 4 modi proposti, a seconda del numero di matricola:

1. pendolo semplice
2. cerniera
3. doppio pendolo
4. incastro

Durante lo svolgimento dell'esercizio (nel calcolo delle sollecitazioni con Castigliano) il cappello deve essere trattato come una trave puramente flessionale ad asse curvo ed a sezione costante (rettangolare in questo caso); tuttavia, poiché la variazione di lunghezza tra le fibre interne ed esterne è molto contenuta, possiamo trattarlo utilizzando la teoria della trave diritta.
Anche la prima parte del fusto può essere vista come una trave sottile incastrata al resto del corpo della biella, sebbene abbia una geometria tozza e curva.

Come parametri per lo svolgimento dell'esercizio utilizziamo:

• r_m = raggio medio della testa di biella
• h = altezza della trave (nel piano di studio)
• b = profondità della trave (spessore fuori piano)

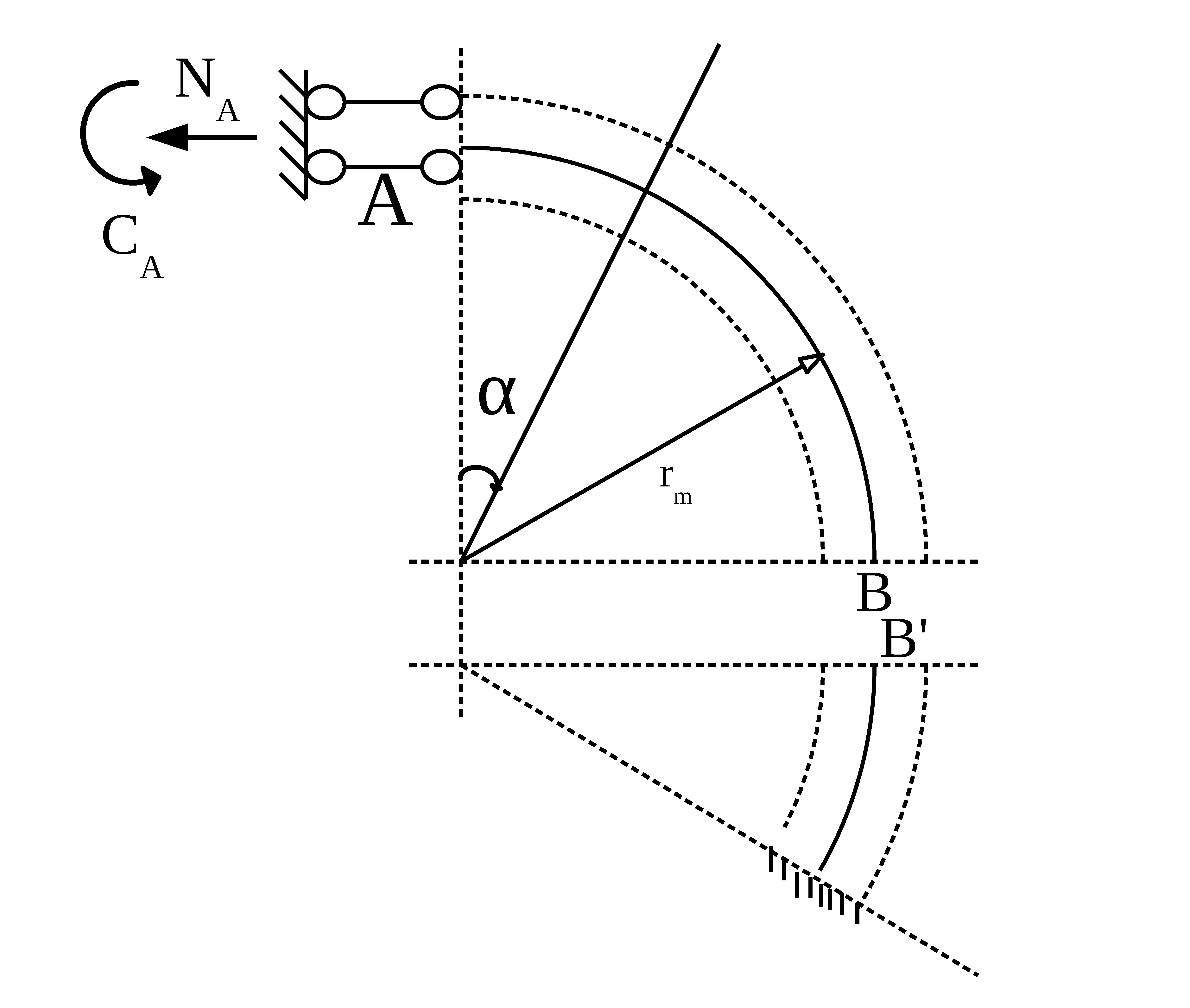
Di seguito potete vedere la rappresentazione della struttura in esame, con la sola omissione del vincolamento tra B e B'.
Per ragioni di simmetria viene rappresentata, dunque sottoposta al calcolo, solo metà della vera testa di biella.

A questo punto definiamo le reazioni vincolari, ovvero le incognite del problema:
-nel punto A, sull'asse di simmetria, immaginiamo una connessione con la restante parte del cappello tramite un doppio pendolo che darà luogo a due reazioni vincolari:

• N_a = reazione di sforzo normale
• C_a = coppia di reazione

-nel punto B di connessione tra cappello e fusto, a seconda del numero di matricola, possiamo avere i 4 tipi di vincolamento sopra descritti che porteranno altre reazioni vincolari: essi potranno (in 3 casi su 4) far insorgere reazioni iperstatiche.

1. bielletta (pendolo semplice): aggiunta di una sola reazione di sforzo normale (N_b) , rendendo così la struttura isostatica.
2. cerniera: aggiunte due reazioni vincolari, una di sforzo normale (N_b) e una di taglio (T_b), che porteranno un grado di iperstaticità.
3. doppio pendolo: aggiunge due reazioni vincolari, sforzo normale (N_b) e una coppia (C_b), che danno un grado di iperstaticità.
4. continuità materiale (incastro): due gradi di iperstaticità, essendo aggiunte tre reazioni vincolari: N_b, T_b, C_b.

NOTA: Se ci fosse continuità fra testa e cappello, il sistema sarebbe 3 volte iperstatico (sarebbe un arco chiuso infatti) ma siccome il carico è simmetrico tolgo il taglio in A introducendo un bipendolo.

Occorre ora stabilire la forma del caricamento imposto al cappello, che nella realtà è provocato dalla combustione e/o dalle forze di inerzia del gruppo pistone-spinotto-biella. In letteratura esistono tre modelli per la distribuzione di pressione applicata alla superficie interna del cappello:

1. soluzione alla Kolkin: viene ipotizzato un caricamento a pressione costante, p(α)=p₀ (considerando una coordinata angolare α, positiva in senso orario e nulla nel punto A), dell'arco superiore della testa; considerando una seconda coordinata angolare θ, positiva in senso orario e nulla nel punto A, possiamo ritenere la struttura caricata per 0<θ<π/2.
2. soluzione alla Giovannozzi: si ipotizza un caricamento a pressione variabile con la quota angolare, p(α)=p₀cos²(α), sempre sull'arco superiore della testa (0<θ<π/2).
3. soluzione alla Demidov-Kolkin: viene ipotizzato un caricamento a pressione costante, p(α)=p₀, su una parte inferiore di geometria: 0<θ<π/4.

DOMANDA: se cambio il tipo di caricamento, pur generando la stessa forza risultante verticale, cambia anche lo stato tensionale nella biella?

• Se la struttura è isostatica, lo stato deformativo (dunque tensionale) nella zona ESTERNA a quella in cui avviene il cambio di caricamento NON VARIA, purché il nuovo caricamento produca la medesima risultante.

In base a questa regola, nel caso di vincolamento tra cappello e fusto con pendolo semplice, il passaggio da un caricamento a un altro non produrrà effetti nella metà inferiore della testa, dato che il cambio di distribuzione di pressione interessa solo la parte superiore. Pertanto, per studiare le tensioni nel fusto si potrebbe perfino evitare di considerare un particolare caricamento, sostituendolo con la sola forza risultate, ottenendo così un problema molto più semplice.
Negli altri casi (iperstatici) invece le tensioni interne dipenderanno dal tipo di carico in tutta la struttura.

A titolo di esempio, si pensi al caso della seggiovia esposto nel libro “Costruzione di macchine” del prof. Strozzi: se sostituiamo i carichi P/2 di due persone a sedere con una sola forza P (somma delle due) applicata nel baricentro dei due carichi precedenti, si vede come il momento flettente nel resto della struttura non subisca variazioni, se quest'ultima è isostatica. Se si aggiunge ad esempio un carrello sotto al sellino si iperstaticizza la struttura, e il momento flettente non sarà più indipendente dal tipo di carico nel braccio della seggiovia.

Ora che il problema è stato impostato inizia lo svolgimento dei calcoli. Come primo passo si calcola la forza P risultante derivante dalla distribuzione di pressione; di essa interessa solo la componente verticale, dato che a causa della simmetria del problema la componente orizzontale agente su una mezza testa si annullerà con quella dell'altra mezza, mentre sarà quella verticale a scaricarsi sul resto della biella e ad essere equilibrata dalle reazioni vincolari.
P si calcola con un semplice integrale:

$P=\int\limits_a^b p(\alpha) \cdot r_m \cdot b \cdot \cos(\alpha) \mathrm{d}\alpha$

dove:

• Caricamento 1: $p(\alpha)= p_0$ ; $[a;b]=[-\frac{π}{2};\frac{π}{2}]$
• Caricamento 2: $p(\alpha)= p_0 \cdot \cos^2(\alpha)$ ; $[a;b]=[-\frac{π}{2};\frac{π}{2}]$
• Caricamento 3: $p(\alpha)= p_0$ ; $[a;b]=[-\frac{π}{4};\frac{π}{4}]$

$r_m \cdot \mathrm {d}\alpha$ rappresenta l'arco infinitesimo su cui agisce la pressione p(α). Otteniamo così una forza, la cui componente verticale viene calcolata mediante il prodotto con il cos(α). Infine si moltiplica il tutto per lo spessore intrapiano b.

La risultante di pressione P sarà dunque una funzione lineare della distribuzione di pressione p₀.

Per stabilire quali equazioni sono necessarie per l'identificazione delle incognite del problema è necessario fare alcune distinzioni tra i vari casi di vincolamento tra il cappello e il fusto:

Il caso di vincolamento tramite pendolo semplice rende la struttura isostatica perciò, tramite le equazioni di equilibrio, è possibile ricavare il valore delle nostre 3 incognite:

1. N_a = $\int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} p(\alpha) \cdot \sin (\alpha) \mathrm{d}\alpha$
2. N_b = $\frac{P}{2}$
3. C_a = $\int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} p(\alpha) \cdot r_m \cdot b \cdot r_m \cdot \sin (\alpha) \mathrm{d}\alpha + N_b \cdot r_m$

Riguardo al calcolo di C_a, all'interno dell'integrale, valuto la forza come prodotto tra l'arco e lo spessore su cui agisce la pressione p(α) e la moltiplico per il suo braccio rispetto al punto A ($r_m \cdot \sin(\alpha)$) a cui sommo la componente di momento flettente dovuta alla reazione vincolare in B.
Per convenzione, i contributi di coppia sono positivi se portano in trazione l'estradosso.

In questi casi non basta l'imposizione delle equazioni di equilibrio ma è necessario imporre adeguate condizioni di congruenza degli spostamenti dei punti vincolati.
Come prima cosa attraverso le equazioni di equilibrio della struttura è necessario esprimere un'incognita iperstatica in funzione delle restanti:
$C_a= f (P, N_a)$ o viceversa.
Successivamente è necessario imporre come condizione di congruenza (a seconda delle condizioni di vincolo):

• spostamento nullo in direzione x del punto A, se voglio trovare N_a
• rotazione nulla allo stesso punto, se si vuole C_a

Nel caso dell'incastro, che possiede due gradi di iperstaticità, sarà necessario imporre entrambe le relazioni appena descritte, ovvero un sistema di due equazioni in due incognite.

Data la presenza di un'incognita iperstatica diventa necessario definire l'energia potenziale elastica della struttura per poter trarre le informazioni necessarie per il calcolo del momento flettente. Il Teorema di Castigliano offre un'alternativa all'uso delle condizioni di congruenza.

Come primo passo, è necessario identificare il momento flettente che grava su ogni sezione della struttura, che per inciso è anche un dato di interesse. Per fare questo ci serviremo di due variabili angolari: θ è l'angolo che identifica la sezione a cui è riferito il momento flettente, mentre α è una variabile ausiliaria che spazia nel campo di θ.
Considerando positivo il momento flettente che tende le fibre all'estradosso, possiamo scrivere per il tratto caricato:

$M_{f1}(\theta)= C_A + r_m \cdot (1-\cos\theta) \cdot N_A - \int\limits_0^\theta r_m \cdot \sin(\theta-\alpha) \cdot p(\alpha) \cdot b \cdot r_m \mathrm{d}\alpha \hspace{2cm} \theta \in [0;\alpha_{max}]$

dove considero la forza infinitesima dovuta alla pressione $dF = p(\alpha) \cdot b \cdot r_m \cdot d \alpha$ e come suo braccio $r_m \cdot \sin(θ-α)$.
L'estremo superiore di integrazione varia a seconda del caricamento e vale π/2 per caricamenti alla Kolkin o alla Giovannozzi mentre vale π/4 in caso di caricamento alla Demidov-Kolkin (sarebbe il massimo angolo α a cui è applicata pressione).
Mentre per il tratto scarico l'equazione del momento flettente risulta:

$M_{f2}(\theta)= C_A + r_m \cdot (1-\cos\theta) \cdot N_A - \int\limits_0^{\alpha_{max}} r_m \cdot \sin(\theta-\alpha) \cdot p(\alpha) \cdot b \cdot r_m \mathrm{d}\alpha \hspace{2cm} \theta \in [\alpha_{max};\theta_{max}]$

dove $\theta_{max}=$angolo d'incastro

Dato che non ho forze esterne applicate nella congiunzione B-B', le equazioni appena viste valgono anche nel tratto di fusto che è stato simulato. Per questo posso calcolare il momento flettente fino all'incastro.

Usando entrambe le espressioni di M_f calcolo l'energia potenziale elastica totale della struttura:

$U=\int\limits_0^{\alpha_{max}} \frac{M_{f1}^2(\theta)}{2EJ}\cdot r \mathrm{d}\theta + \int\limits_{\alpha_{max}}^{\theta_{max}} \frac{M_{f2}^2(\theta)}{2EJ}\cdot r \mathrm{d}\theta $

NOTA: In Maxima è possibile scrivere un'unica equazione definita a tratti, ma risulta più comodo usare due equazioni distinte per il momento flettente e sommare poi i contributi all'energia elastica.

Grazie al Teorema di Castigliano si trovano facilmente le condizioni da imporre per determinare le incognite iperstatiche:

$\frac{\partial}{\partial N_A}(U)=0$

$\frac{\partial}{\partial C_A}(U)=0$

NOTA per MAXIMA: quando andiamo a differenziare una variabile con Maxima, anche se abbiamo definito in precedenza y=3x², il programma opererà in questo modo:
diff(y+x,x,1)=1
diff(3x²+x,x,1)=6x+1
Dunque, attenzione a come effettuate le derivazioni! Fate la valutazione di ogni singolo termine che compare nell'espressione da derivare!

La seconda parte della lezione ha riguardato l'analisi dei risultati ottenuti dal modello FEM del piede di biella, con spinotto e bronzina, focalizzando l'attenzione su alcune curiosità del problema.

Tra la bronzina e lo spinotto vi è presente un gioco diametrale di 8 centesimi verso il basso, mentre nella parte alta c’è contatto non lungo le intere superfici di interfaccia, ma teoricamente su un solo nodo (nella realtà c'è una superficie di contatto, secondo la teoria di Hertz). Per ottenere una condizione del genere si parte da una geometria corretta che viene costruita sul nominale e poi aggiunta la tolleranza. Inoltre il caricamento è di 10000N su metà piede.

Purtroppo questo nodo in comune non è fisso durante la simulazione di un intero ciclo di lavoro del pistone: quando viene applicato un carico trattivo allo spinotto, verso l'alto nel nostro modello, il contatto avviene nel nodo posto sul piano di simmetria nella parte superiore della superficie interna della bronzina, per cui il gioco “si concentra” nella parte bassa dell'accoppiamento; ma quando avviene l'inversione del carico (compressivo), il nodo di contatto è quello diametralmente opposto.

Nel momento esatto dell'incrocio, si ha un distacco dello spinotto della bronzina, per permettere questo scambio di punti di contatto: in altri termini, il programma sgancia tutti i link precedentemente imposti poiché registra una tensione trattiva su di essi, per poi ricrearli ove si generi compenetrazione di materiale Il piede di biella è un corpo elastico posizionato nello spazio solo finché tocca lo spinotto, attraverso la bronzina, poiché è ad esso che sono stati assegnati i vincoli di posizionamento. Pertanto, nell'istante dell'incrocio, il piede diventa un corpo labile e la sua matrice di rigidezza diviene singolare, interrompendo l'analisi e il solutore rilascia l’errore 2004.

Se il contatto è necessario per posizionare uno dei corpi, che nel nostro caso serve per posizionare nello spazio il piede, occorre che dall’istante 0 i due corpi si tocchino. In assenza dei link generati dinamicamente una volta riscontrati il contatto dei due corpi, il piede è labile. Se parto da questa condizione e comincio ad applicare una forza trattiva, questi link inizialmente attivati perché c’è contatto a fronte di carichi trattivi vengono sganciati fino a quando tutti i link sono sganciati, i due corpi non si toccano piú e la matrice diventa singolare: si avrebbe impossibilità di simulare una condizione sinusoidale della zona inferiore perché all’inversione di carico si ha un sistema di vincoli che si attivano appena si inverte il carico in modo da prendere il carico dall’altra direzione.

SOLUZIONE non simulo l'intero ciclo di carico del gruppo pistone, ovvero non simulo il momento dell'incrocio. In quell'istante infatti la struttura è scarica, dato che non abbiamo trasmissione di forze tra spinotto e resto della biella; pertanto possiamo simulare il ciclo spezzandolo in tre parti:

1. Parto dal modello con i link di contatto per il carico compressivo e applico tale carico (opportunamente modulato) fino al suo annullamento prima dell'incrocio
2. Spostamento rigido dello spinotto per farlo andare nella configurazione trattiva
3. Applicazione del carico trattivo (modulato anch'esso)
4. Questo percorso di simulazione non verrà affrontato, ma ci si limiterà a vedere il solo caricamento trattivo.

RISULTATI CASO TRATTIVO

L’istante 0 è un istante scarico che serve ad attivare i link prima che il sistema diventa labile. Il solutore vede il contatto iniziale su una certa area, poiché i nodi sono più vicini di una certa tolleranza, ossia la Distance Tollerance. Quando i nodi sono più vicini di questa distanza sono agganciati i link. Partendo dai 4 link iniziali, se uno di questi avrà un collegamento trattivo verrà sganciato.

Dopo aver applicato la prima frazione di carico, ossia dopo 1/100 di tempo e con 1/10 di carico, i link subiscono una condizione trattiva e vengono sganciati con uno solo che rimane ancora agganciato. L’area di contatto, a questo punto, sarebbe di difficile definizione perché va da 0 ad 1 elemento, con un errore dovuta alla risoluzione ridotta. Ad un certo punto l’area di contatto evolve. All’incremento 100, tempo 1 applico il carico di 10000N, ottenendo un sovraccarico, con la riultante delle forze visualizzata su un HISTORY PLOT (Si acquisiscono solo i dati globali di modello con la varibaile sull’asse x tempo e su l’asse y forze in direzione y sulla bronzina). All’istante 2 si ha un carico di 40000N: in tal modo ci si rassicura che la pressione applicata al fusto dia come risultante su mezzo piede 10000 N conoscendo la legge; si tratta di un termine di controllo utile ai fini del calcolo.

Considerando le pressioni di contatto si osserva che pur non arrivando ad un contatto pari a pi/2, le pressioni non sono alla Giovannozzi ma alla Davidov Kolkin e vanno fino a pi/4 come il caso dell’esercizio precedente. Modellando un sovraccarico, il sistema si comporta in modo che la pressione di contatto continua a crescere fino a carichi sufficientemente alti dove continuerà a cresce lentamente. Il sistema approccia la distribuzione di pressione di quella in assenza di gioco. La condizione asintotica che si ottiene per carichi elevati in presenza di gioco è analoga a carichi finiti in assenza di gioco. Lo stato tensionale della struttura viene monitorato al punto più tensionato del piede (per vederlo si vedono i valori numerici dei nodi) in funzione del carico applicato alla struttura. Anche in questo caso si effettua un HISTORY PLOT, settando tutti gli incrementi e imponendo sull’asse x il Carico applicato al corpo, e sull’asse y la Equivalent Von Mises Stress. Si note che seppur debolmente il sistema è non lineare perché la biella viene vista come se fosse una trave, dove per i carichi è diverso applicare un carico concentrato ad un carico distribuito.

RISULTATI CASO COMPRESSIVO

Se si considera il caso compressivo si nota lo stesso comportamento del caso trattivo solo che il carico è applicato nella zona inferiore e il gioco è nella parte alta. Inizialmente si avranno 4 nodi a contatto che man mano si sganciano con l’area di contatto che si evolve fino ad approcciare il caso in assenza di gioco.