dati geometrici piede biella:

• diametro interno piede 22.5 mm
• diametro esterno piede 30.5 mm
• diametro interno bronzina 20.5 mm
• spessore assiale piede 21.86 mm

materiale acciaio, tensione critica per cicli all'origine 800 MPa.

Spinotto:

• diametro interno 10.5 mm
• accoppiamento con gioco diametrale 0.08 mm
• lunghezza assiale 46 mm

Carico:

• a trazione 14 kN
• a compressione 32 kN

modello a fine lezione scorsa

biella_cfd_cattedra_v009_speriamo.mud

Scarichiamo e apriamo il file della lezione precedente:

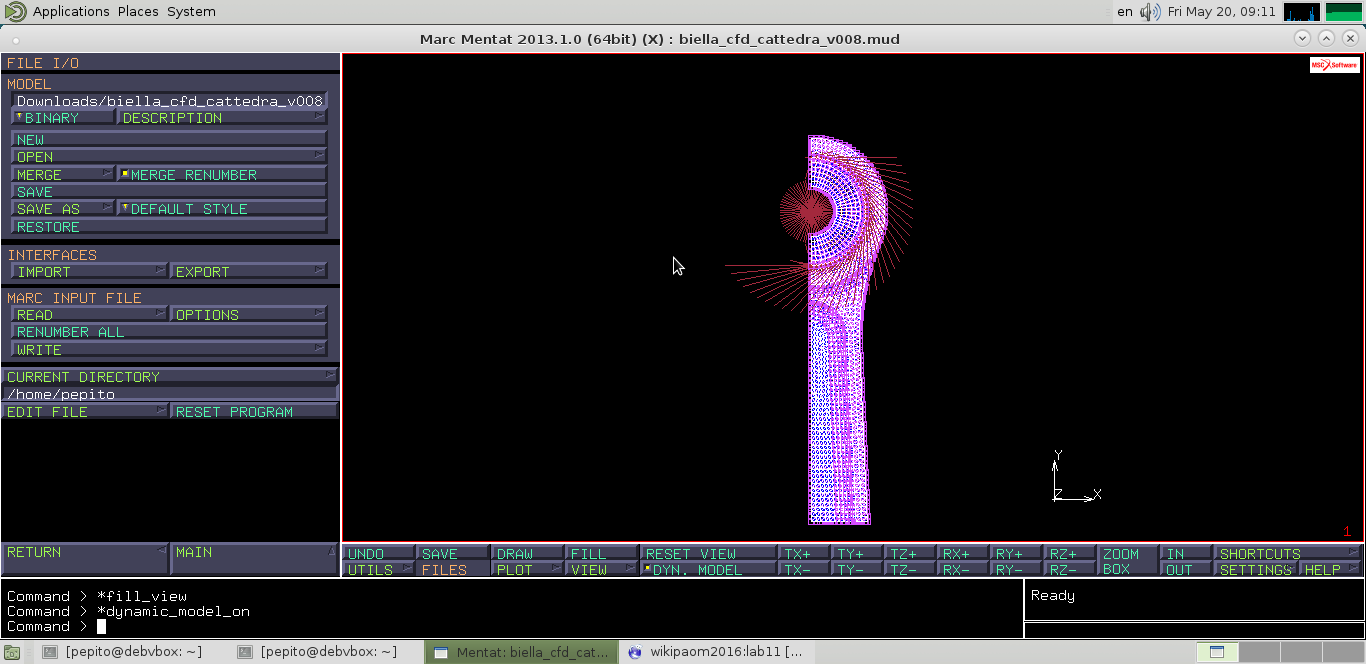
Le boundary conditions del blocco dei nodi ausiliari impone un’aderenza tra le superfici interne del piede e superfice esterna della bronzina; altri vincoli sono i vincoli di simmetria sul piano <yz> sia per i nodi con sistema di riferimento cartesiano <xyz>, sia per i nodi dov'è stato inserito un sistema di riferimento cilindrico; abbiamo un vincolo di simmetria nel piano <xy>, un vincolo che impone la planarità della sezione di interfaccia con la testa di biella e una pressione distribuita nelle aree di contatto tra pistone e spinotto la cui risultante è stata calcolata in modo da essere 14kN. Spinotto e bronzina sono costruiti con 8 centesimi di gioco, e lo spinotto è stato posizionato in modo che il punto di incipiente contatto, in questa zona i corpi spinotto e bronzina si toccano all'istante zero. Quindi bisogna ricordarsi di portare i corpi almeno in incipiente di contatto, altrimenti il tratto che i corpi compiono prima di arrivare al contatto è moto di corpo rigido che produce una singolarità. Avevamo dato una pressione definita come: carico/area diametrale= 28.568 che è stata modulata nel tempo con una tabella di tipo quadratica dove il carico non viene applicato in un solo colpo.

In un grafico t/p il carico di 28.5668 è raggiunto solo nel tempo 1 di simulazione e la legge di simulazione è di tipo parabolico in modo tale da avere piccoli incrementi di carico costanti quando l’area di contatto è ridotta e quando l’area cresce recupero a passi più grossi la differenza di carico che ci rimane.

Dove lanciando l'algoritmo del N-R, questo risolve la struttura partendo da un carico, non troppo lontano (almeno a livello di carico applicato) da quello d’arrivo. Vediamo che ci sono dei nodi in posizioni strane, abbiamo ri-scalato lo spinotto per avere il gioco al collegamento con la boccola, purtroppo ci sono rimasti questi nodi spuri che devono essere eliminati, perciò effettuiamo un: REMOVE > UNUSED NODES. Successivamente facciamo uno SWEEP con tolleranza 0.01, cosa che altrimenti non posso fare dopo l’impostazione del contatto: MESH GENERATION > SWEEP

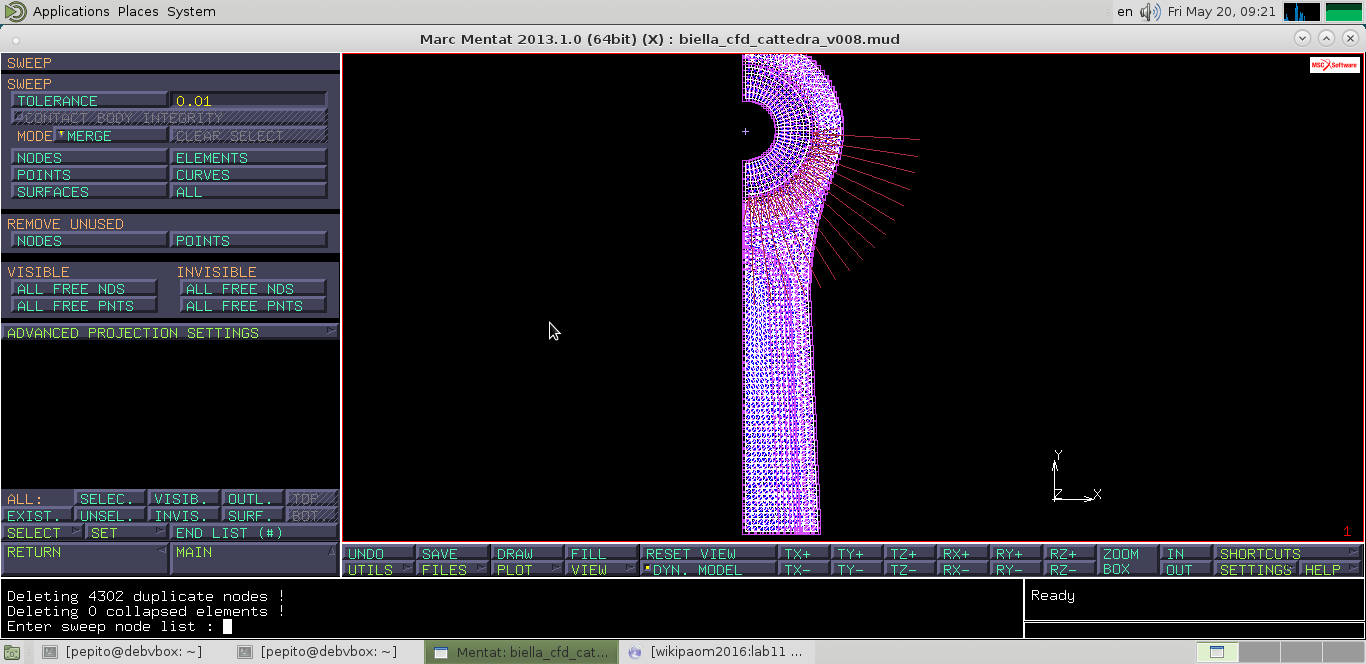
Ricordandoci che abbiamo un solo UNDO, conviene salvare il file usando dei nomi incrementali. Dobbiamo impostare il contatto tra spinotto e boccola e per farlo bisogna portare i due corpi a toccarsi. Come prima cosa controllo che vi siano dei SET per distinguere i vari elementi, allora vado in: MAIN MENU > MESH GENERATION > SELECT > ELEMENTS > STORE

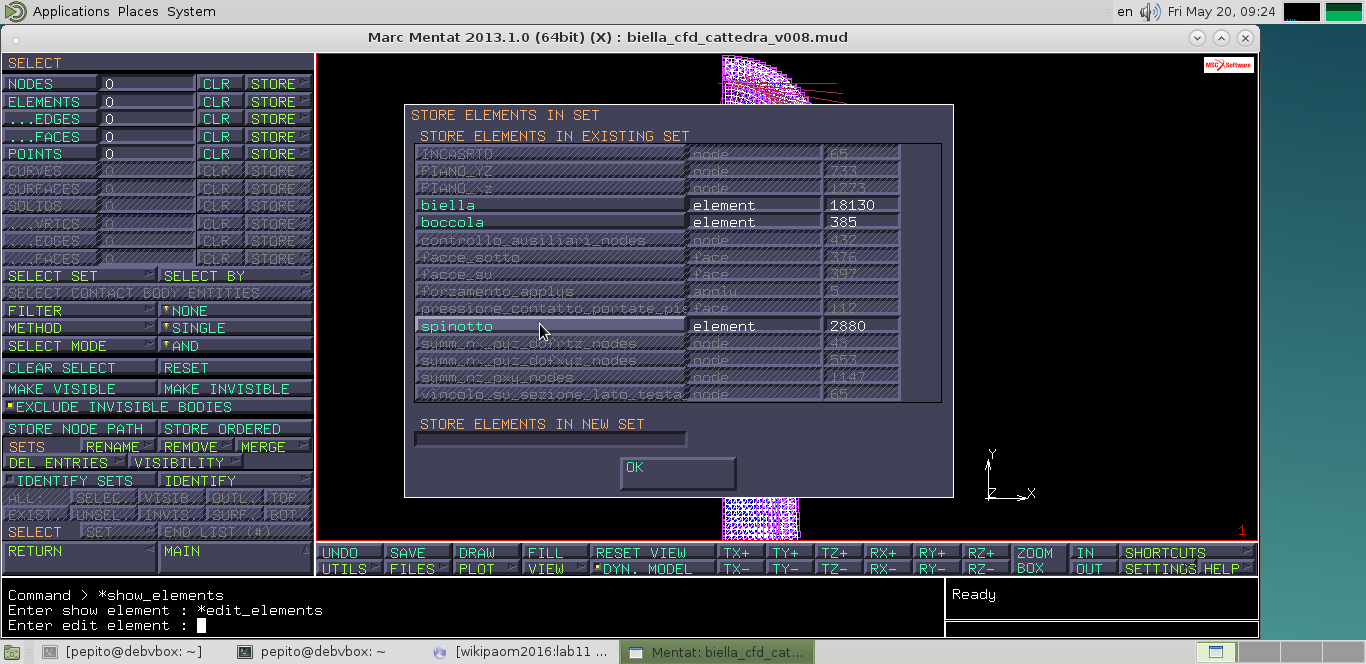
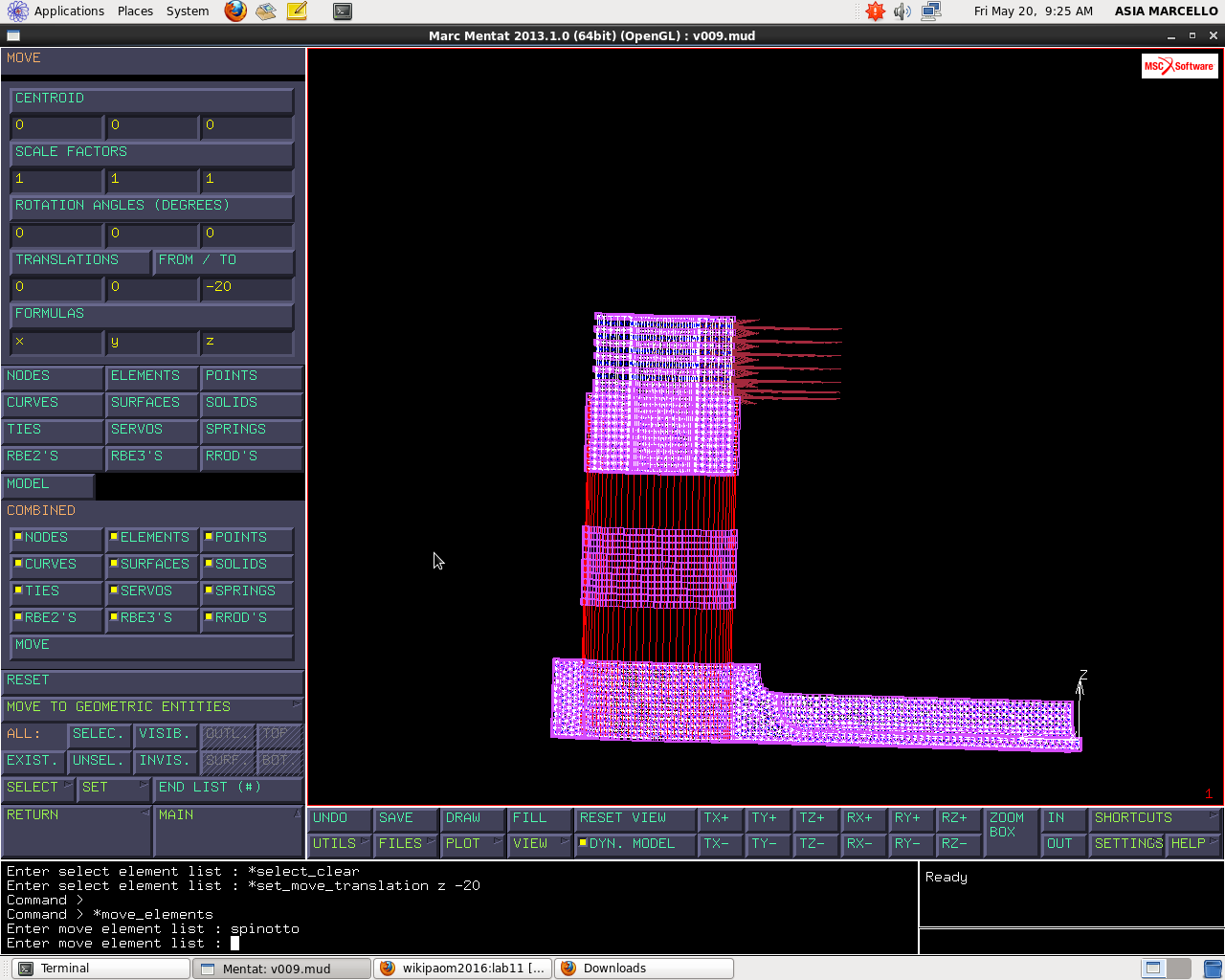
Verificato che ci sono i set, andiamo a spostare lo spinotto; vediamo che ci sono 20mm di distanza in direzione z tra bronzina e spinotto, di conseguenza andiamo in:

MESH GENERATIONS > MOVE > TRANSLATIONS: -20

Mi chiede quali elementi e seleziono quelli dal set creati: SPINOTTO.

Ora dobbiamo spiegare che vi è un vincolo di non compenetrazione tra questi due corpi. La definizione di corpo in Marc-Mentat è un po’ particolare, vi sono due tipi di corpi: rigidi e deformabili. I rigidi sono descritti da entità geometriche (curve o superfici), i deformabili sono degli elementi. Nel nostro caso abbiamo due elementi deformabili che sono il corpo spinotto e il corpo bronzina. Andiamo in: MAIN MENU > CONTATC > CONTACT BODIES Dobbiamo creare due corpi di contatto ambo deformabili: NEW > MESHED DEFORMABLE > NAME: BOCCOLA ELEMENTS > ADD: BOCCOLA (385 elementi)

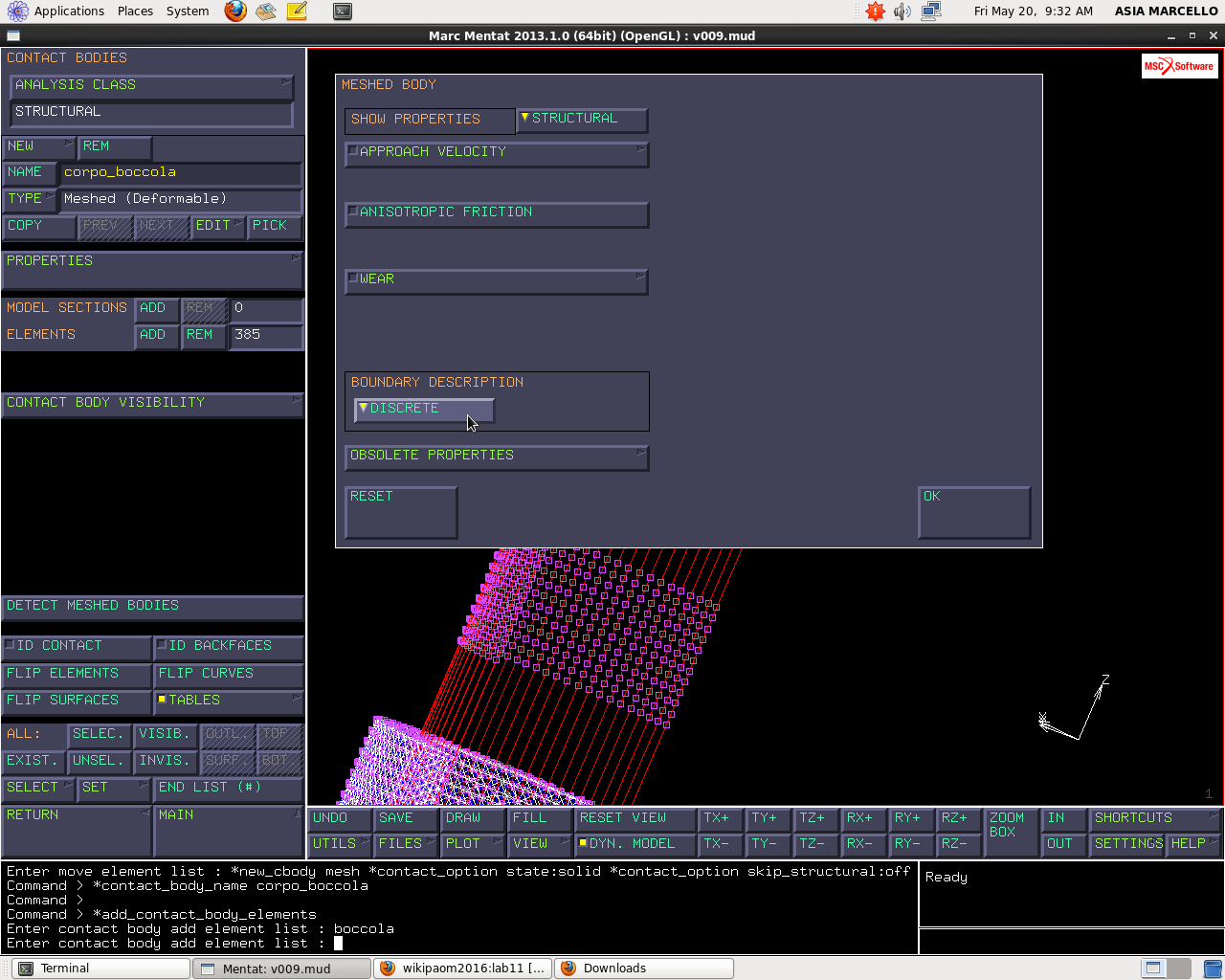
Come proprietà inseriamo BOUNDARY DESCRIPTION > DISCRETE che vuol dire si suppone le superfici del corpo vengano prese dalle facce dell’elemento senza interpolazioni polinomiali; se portiamo in ANALYTICAL le superfici vengono prese come delle pezze polinomiali costruite a interpolare localmente le facce dell’elemento. Creiamo un secondo corpo di contatto, sempre deformabile, di nome CORPO SPINOTTO, a cui sono associati tutti gli elementi del set SPINOTTO. A proprietà selezioniamo ANALYTICAL: di questo copro dobbiamo considerare le superfici, quindi è interessante decidere se le superfici vengono modellate in forma discreta o analitica; mi accorgo che entra in quella casistica di fenomeni che non devono succedere a causa della discontinuità. Se facciamo: IDENTIFY > CONTACT vedo colorate le facce interessate al contatto; Se faccio: PLOT ELEMENTS > SOLID > REGEN; Se faccio: PLOT > ELEMENTS > SETTING >EDGE (non tutti quelli di superfice) ma solo OUTLINE angolo dove ho brusche inclinazioni delle facce degli elementi. Mi vengono visualizzati solo gli elementi dove c’è discontinuità.

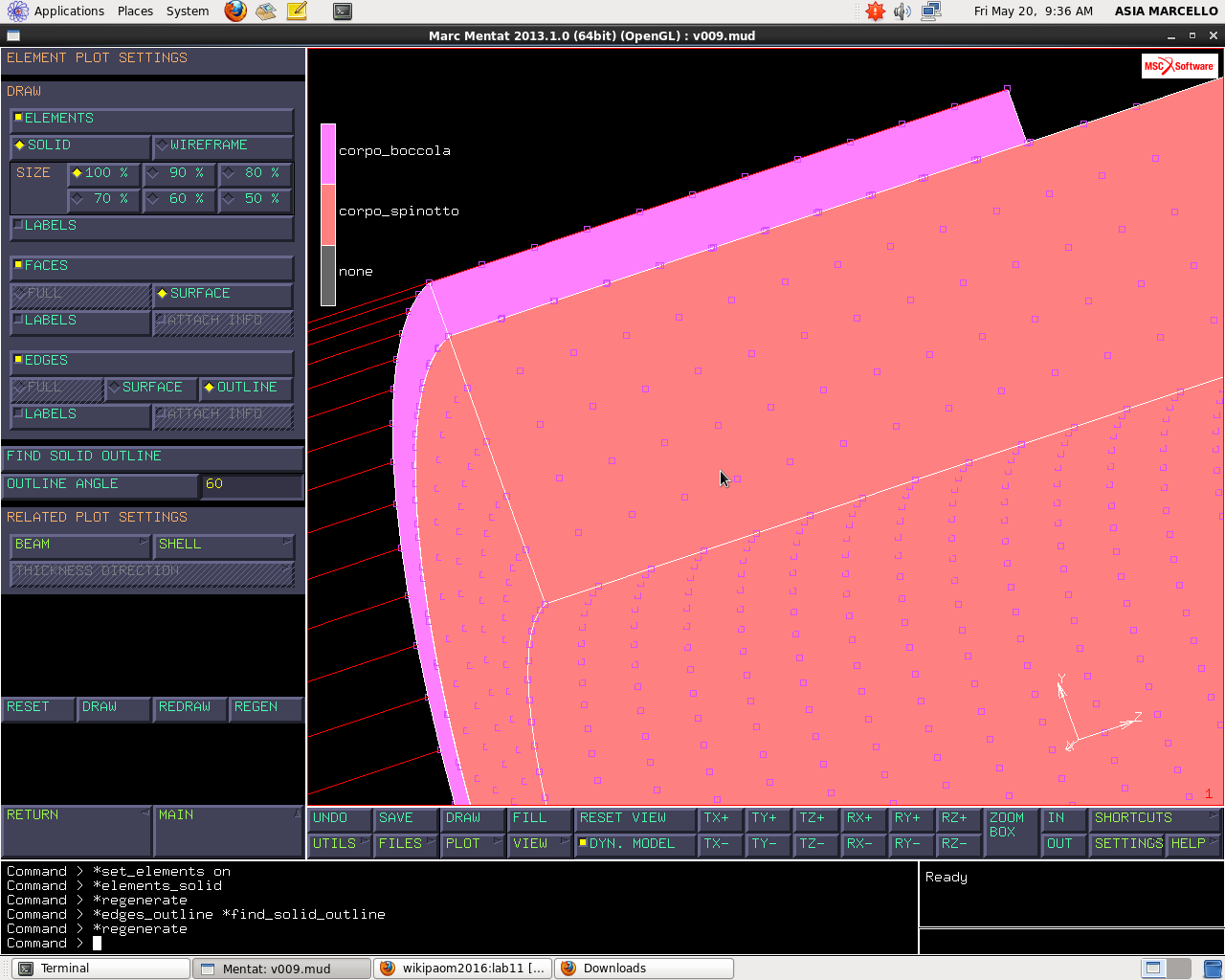
Quindi ritorno in MAIN MENU > CONTACT > CONTACT BODIES > PROPERTIES> BOUNDARY DESCRIPTIONS > SETTINGS

Le discontinuità le rileva in maniera automatica quando vede un angolo soglia di 60°, ma non essendo certi che li vada a individuare tutti, li troviamo ni singolarmente (siamo nel caso 3D quindi le discontinuità sono degli spigoli, se fossimo nel caso 2D sarebbero dei nodi che estrusi fuori piano diventerebbero degli spigoli): DISCONTINUITY > METHOD > MANUAL > 3D EDGES > ADD > ALL >VISIBLE Ci sarebbero anche gli spigoli della bronzina che però non vengono visualizzati perché considera solo il sottoinsieme degli edges che appartengono al corpo spinotto.

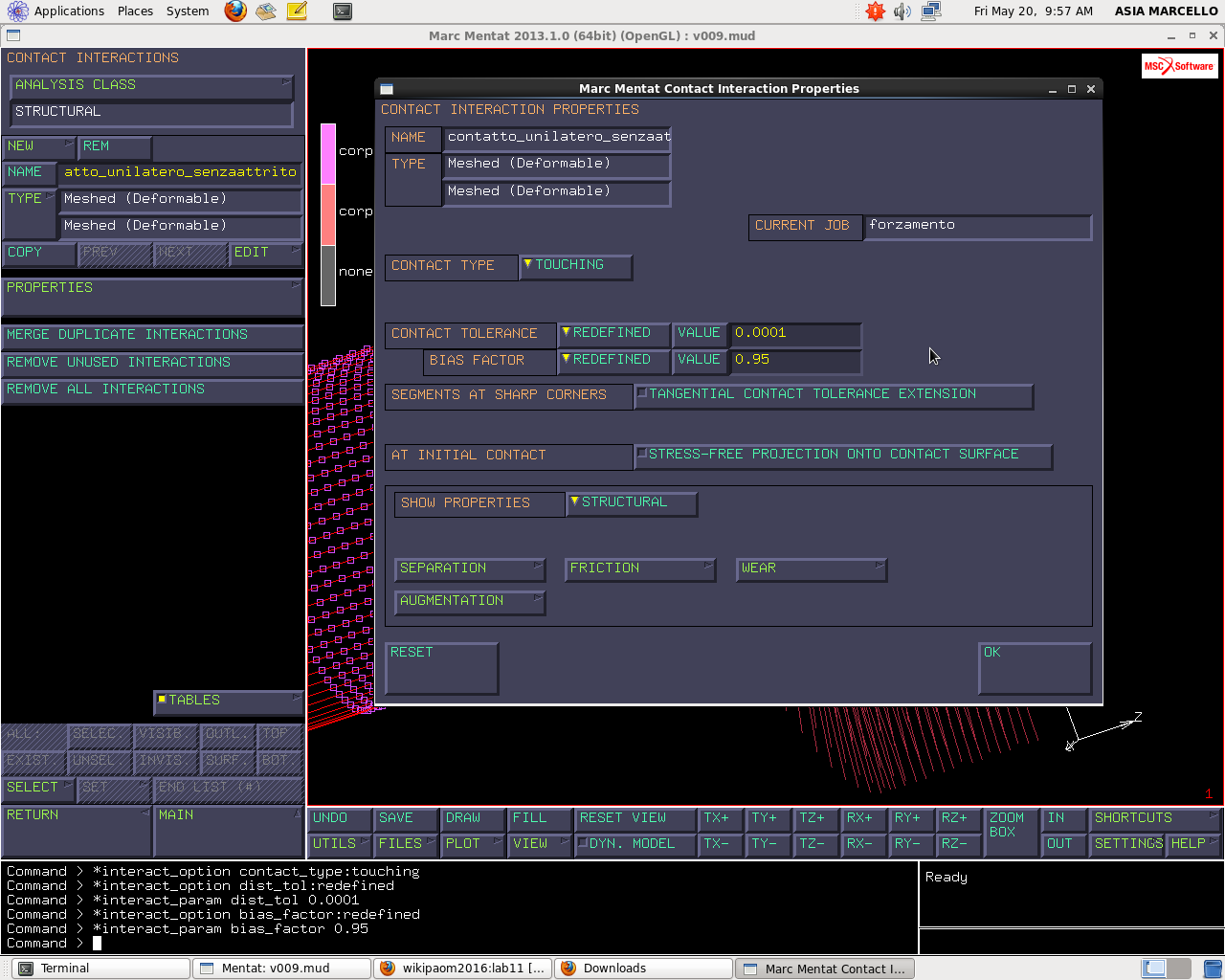
Una volta definito i contact bodies, definiamo le interazioni che ci sono tra corpo e corpo, questo lo facciamo in MAIN MENU > CONTACT > CONTACT INTERACTIONS NEW > MESHED vs MESHED > NAME: contatto unilatero senza attrito PROPERTIES: TOUCHING (contatto monolatero) e GLUED (incollato, contatto bilatero privo di aderenza, che può essere rotto raggiunti certi limiti).

            (inserire immagine distance tollerance)

Il concetto di CONTACT TOLLERANCE merita di essere approfondito: considero un corpo di cui considero la superficie, la tolleranza è una tolleranza nell'intorno di quella superficie: prendo una fascia che comprende una parte un po' sopra e un po’ sotto quella superficie, quella fascia mi va a definire la DISTANCE TOLLERANCE. In questa distance tollerance, è individuato un BIAS FACTOR che definisce la posizione di questa fascia rispetto alla superficie. In particolare abbiamo che, considerando un bias factor come di default di 0.95, abbiamo che: il 2.5% è fuori e il 97.5% è dentro. Quando un nodo è fuori dalla fscia di cui considero i nodi, il nodo non tocca; quando un nodo è fuori dalla fascia ma dentro al corpo potrebbe toccare; quando un nodo entra nella fascia viene considerato in contatto. Non ci si aspetti che vi sia la completa penetrazione, ma una tolleranza di contatto: se la tolleranza è troppo larga i nodi sono considerati in contatto prematuramente, se è troppo piccola probabilmente i tempi di calcolo si allungano perché l’algoritmo del contatto è più complesso. Bisogna inserire quindi una distance tollerance adeguata, di solito si inseriscono delle distance tollerance che vanno da 0.001mm a 0.0001mm sulle mesh. Quindi inseriamo come valore di CONTACT TOLLERANCE: 0.0001 e come BIAS FACTOR: 0.95 di default. Non attiviamo l’attrito, in questa maniera avremo un contatto privo d’attrito.

Definiti i corpi e le interazioni bisogna accorpare il tutto, andiamo in: CONTACT > CONTACT TABLES > NEW > NAME: Tutti i contatti > PROPERTIES In corrispondenza di SECOND i quadretti formano una tabella ad incrocio, dove ogni casella è l’interazione tra il corpo 1 o 2 e se stesso, se selezioniamo le caselle ad incrocio consideriamo l’interazione tra il corpo 1 e il corpo 2. Selezioniamo ACTIVE come tipo di interazione di contatto tra i due corpi, e a CONTACT INTERACTON seleziono l’interazione precedentemente creata: contatto unilatero senza attrito.

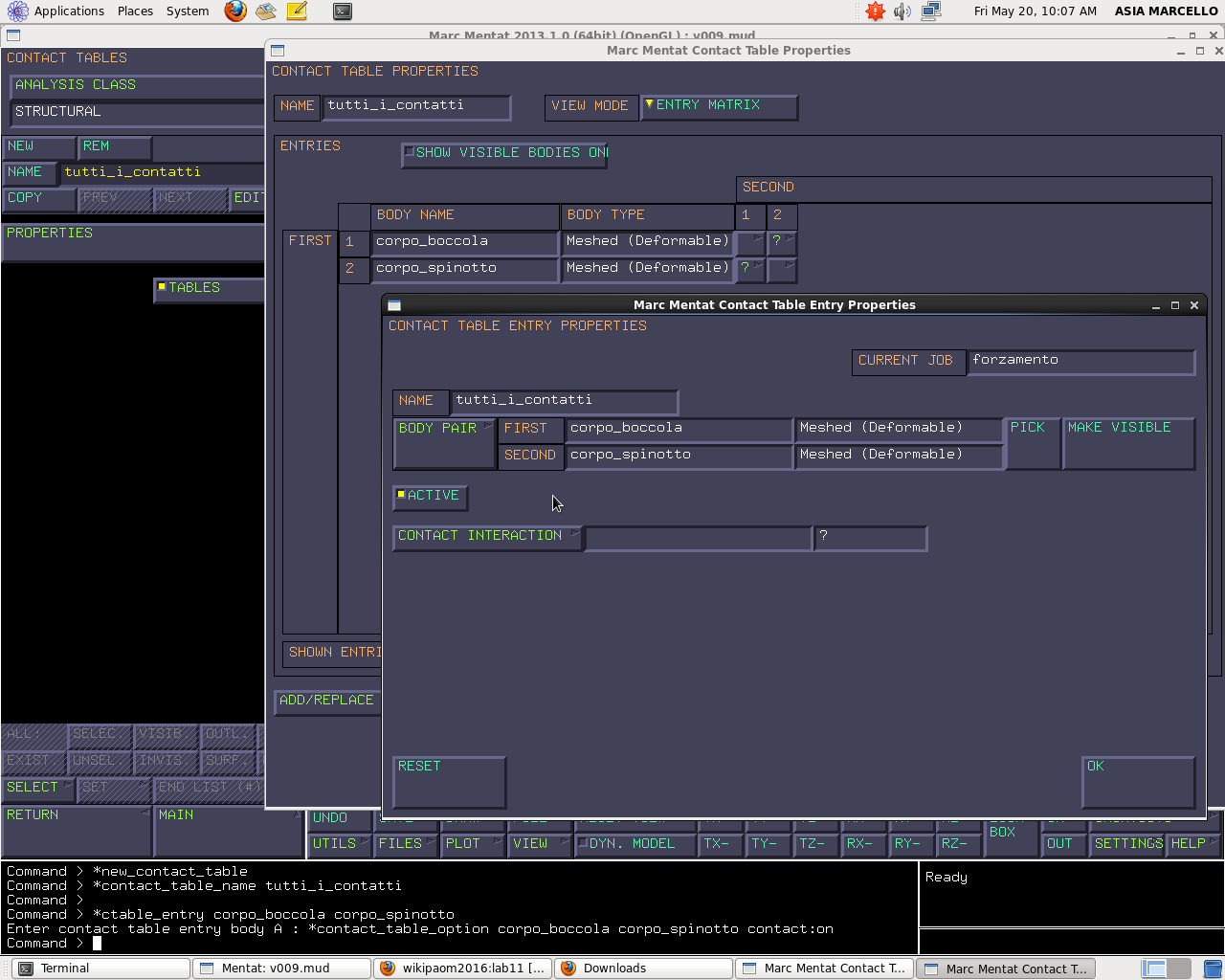
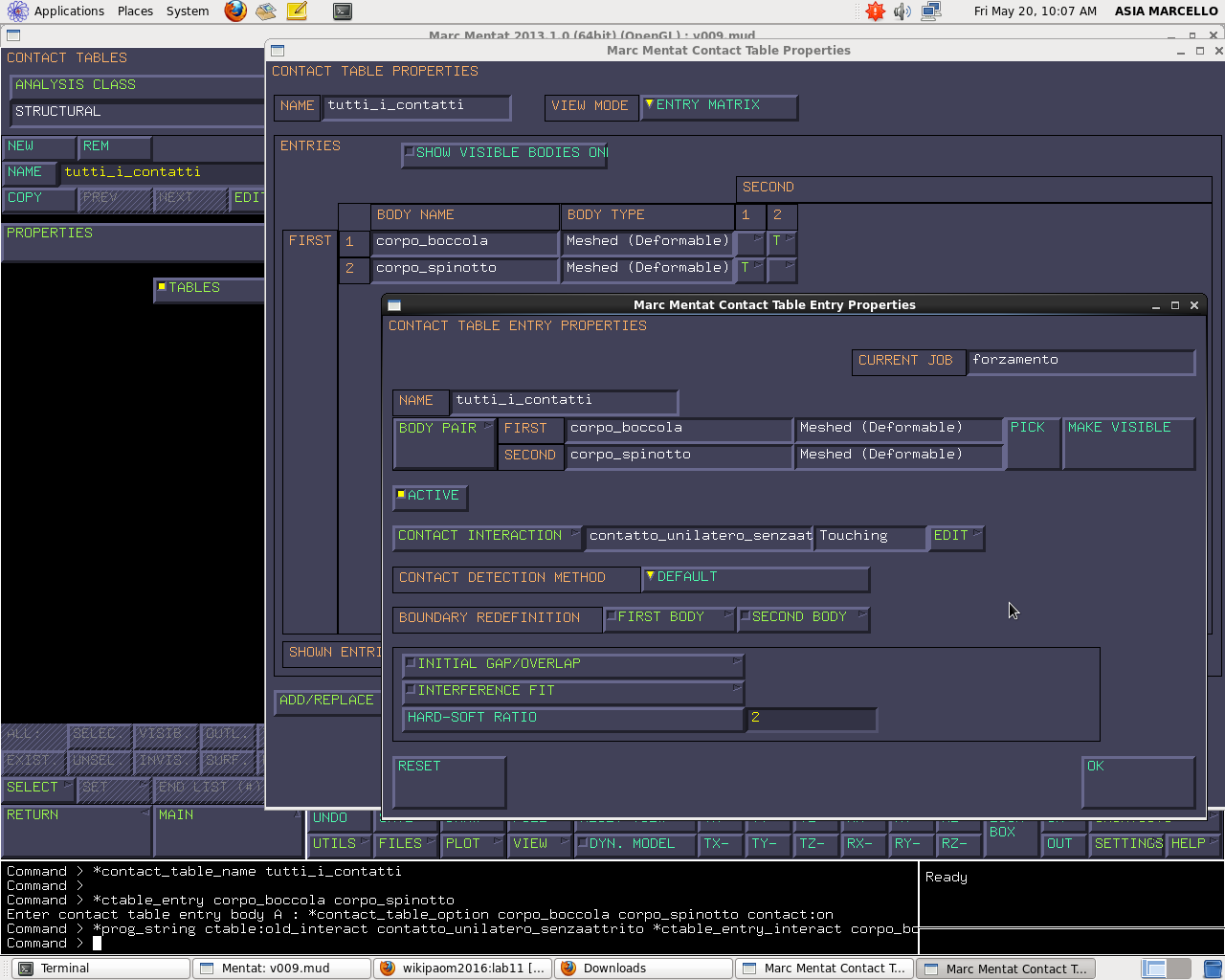
Importante il CONTACT DETECTION METHOD: default (non attendibile, non sappiamo cosa decida), first-second (utilizza i corpi del primo corpo sulle superfici del secondo), second-first (i nodi del secondo corpo sulle superfici del primo); nel nostro caso il corpo first è la boccola, il second è lo spinotto. Noi vogliamo impostare i nodi della boccola sulle superfici dello spinotto, quindi FIRST-SECOND.

A questo punto abbiamo definito l’interazione tra boccola e spinotto, creiamo un LOADCASE. MAIN MENU > LOADCASES > NEW > STATIC > NAME: CARICAMENTO TRATTIVO NON LINEARE (la non linearità è dovuta al fatto che il contatto sia monolatero, l’area di contatto varia con il carico, quindi variano i vincoli, e variando i vincoli varia la matrice di rigidezza e di conseguenza il carico non è lineare). PROPERTIES: LOADS > selezioniamo tutti i carichi; CONTACT > CONTACT TABLES > TUTTI I CONTATTI (Il pezzo di storia di carico utilizzerà quella tabella creata); CONVERGENCE TESTING > impostiamo una tolleranza agli spostamenti dello 0.01; TOTAL LOAD CASE TIME > 1 step dura un secondo e impongo 20 step di carico;

Definiamo il JOB, MAIN MENU > JOBS > NEW > STRUCTURAL > NAME > TRATTIVO; PROPERTIES > INITIAL LOADS e selezioniamo tutte le boundary conditions tranne la pressione di contatto che all'istante zero sarà nulla; all'istante zero questi sono i carichi, a cui seguirà il loadcase :caricamento trattivo non lineare; PROPERTIES > CONTACT CONTROL > METHOD > NODE TO SEGMENT;

FRICTION > NONE (NON VOGLIO ATTRITO)

INITIAL CONTACT ci dice qual è la tabella di contatto da considerare all'istante zero, quindi selezioniamo la tabella: tutti i contatti; in questo modo lo spinotto nasce in contatto con la boccola e si attivano i servo-link dell’interazione. JOB RESULTS chiedo di visualizzare le quantità come da foto seguente:

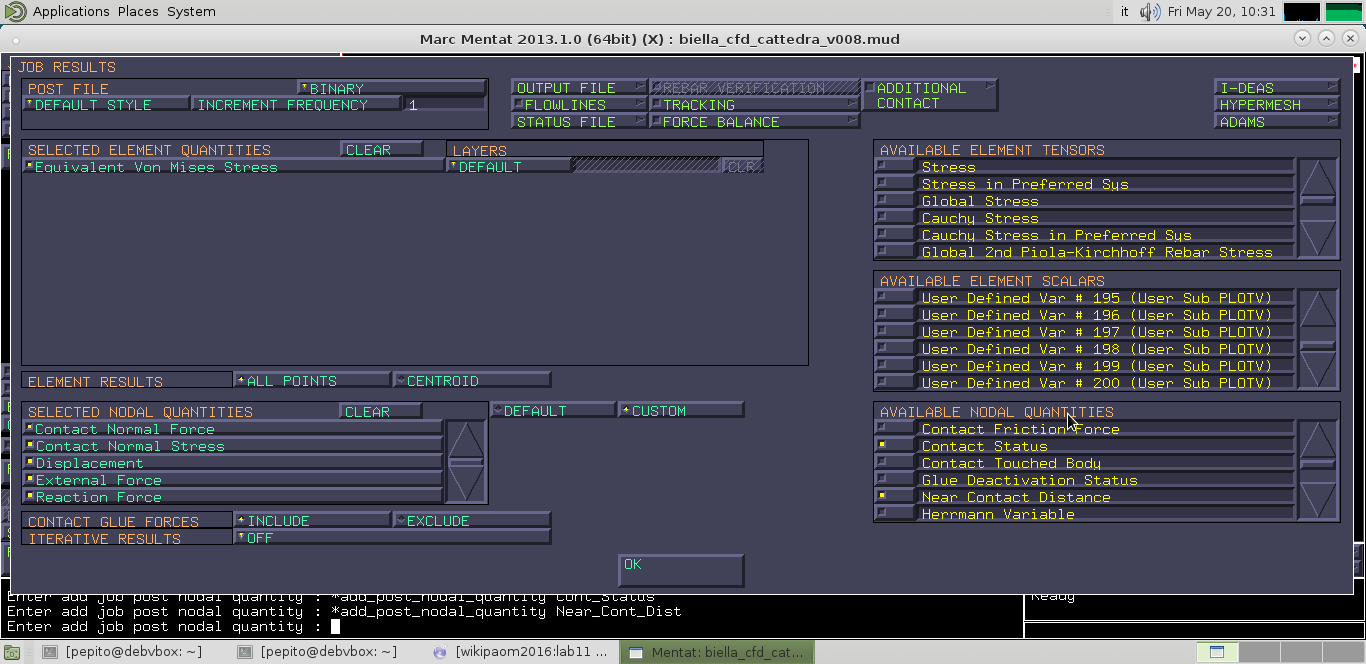
Diamo il RUN:

Si tratteranno di seguito contatti tra due corpi elastici oppure tra un corpo elastico ed uno rigido.

• Contatti progressivi: l’area di contatto cresce all’aumentare delle sollecitazioni applicate o degli spostamenti imposti.
• Contatti regressivi: l’area di contatto cala all’aumentare delle sollecitazioni applicate o degli spostamenti imposti.
• Contatti stazionari: l’area di contatto non varia all’aumentare delle sollecitazioni applicate o degli spostamenti imposti.
• Contatti recessivi: l’area di contatto cala istantaneamente ed in maniera discontinua all’applicazione, anche infinitesima, della sollecitazione. Successivamente resta invariata all’aumentare della stessa.

Esempio: accoppiamento albero-mozzo con spigolo vivo all’interfaccia tra i due corpi

• Contatto stazionario tra albero e superficie interna del mozzo in presenza di interferenza e senza carichi in gioco: all’aumentare dell’interferenza tra i due corpi l’area di contatto non varia (superficie di un cilindro avente come raggio il raggio dell’albero e come altezza la dimensione per cui il mozzo si impegna sull’albero). Il comportamento della struttura è lineare (non è dunque necessario utilizzare il Newton Rapson in presenza di questa situazione)

• Contatto recessivo tra albero e superficie interna del mozzo in assenza di interferenza e con momento flettente ad una delle estremità dell’albero: già per EPSILON INFINITAMENTE PICCOLO si ha distacco nel pt cerchiato (l’albero si flette più del mozzo e si crea una separazione delle due superfici). L’area di contatto comunque non varia all’aumentare del carico anche se il distacco cresce. Il comportamento della struttura è lineare DOPO il distacco, infatti i servo-link di contatto restano tali all’aumentare del caricamento

Esempio: accoppiamento albero-mozzo con spigolo arrotondato all’interfaccia tra i due corpi

• Contatto progressivo tra albero e superficie del interna del mozzo in presenza di interferenza e senza carichi in gioco: al crescere dell’interferenza aumenta il fronte di inizio del contatto.

• Contatto sia progressivo che regressivo tra albero e superficie interna del mozzo in assenza o presenza di interferenza e con momento flettente ad una delle estremità dell’albero; in presenza di interferenza, il contatto nasce progressivo, tuttavia:
  • Nell’estremo superiore, a causa della sollecitazione che tende distaccare le due superfici, diviene regressivo
  • Nell’estremo inferiore, al contrario, la sollecitazione tende a favorire il contatto tra le superfici ed il problema resta progressivo.

Il problema è non lineare in entrambi i casi di contatto progressivo e regressivo.

Nel caso trattato il contatto è progressivo.

Dal running del job osservo che il programma ha svolto 20 step di calcolo con 72 cicli quindi in media si hanno 72/20 iterati di N-R in tutta la storia di calcolo.

Vado in OPEN POST FILE.

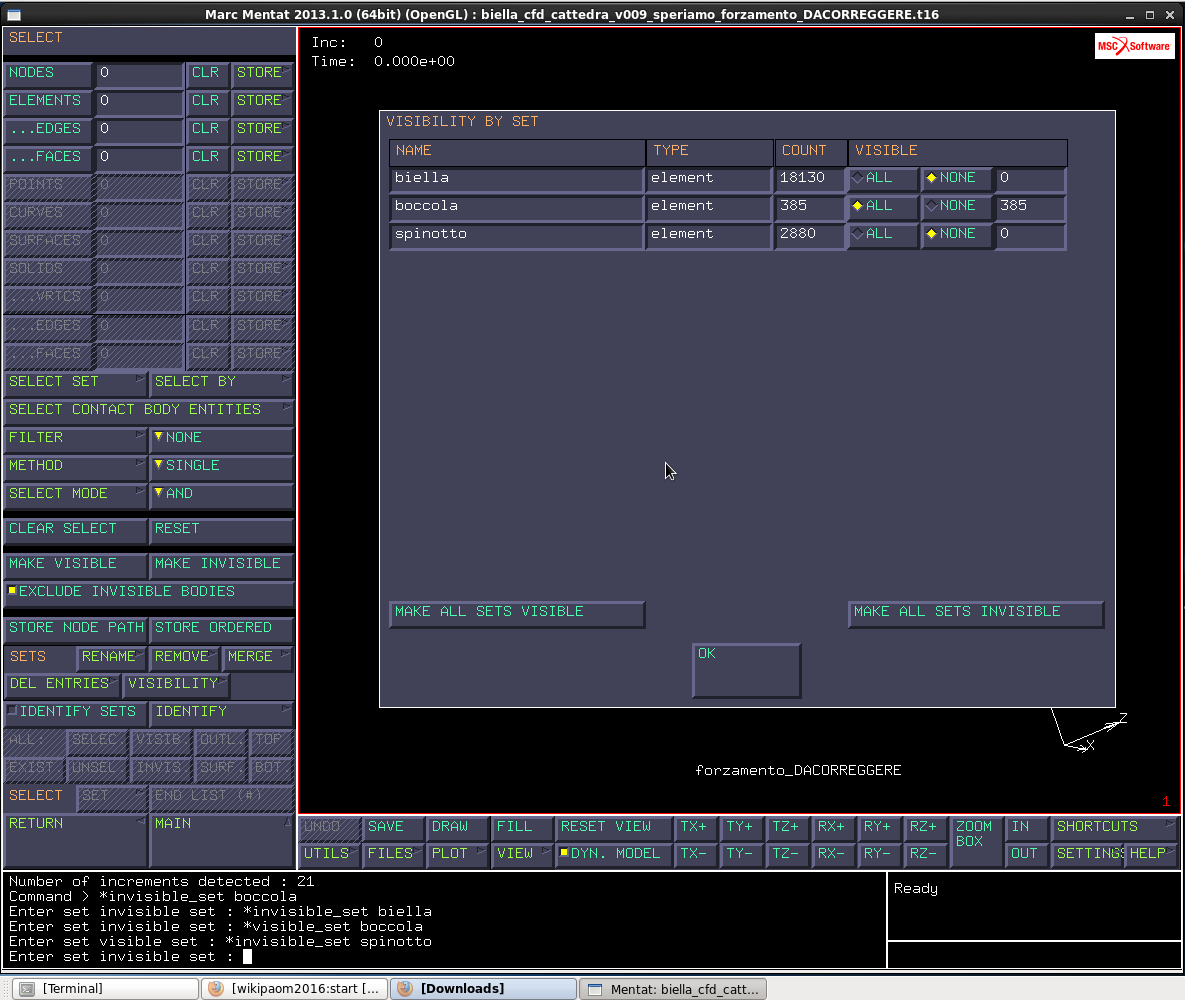
Per visualizzare i risultati relativi alla sola boccola: SELECT > VISIBILITY e seleziono per la boccola ALL, per biella e spinotto NONE.

Siamo interessati all’area di contatto quindi da SCALAR PLOT seleziono come scalar CONTACT STATUS .

Allo step 0 l’area di contatto è estesa alla prima sola fila di nodi essendo il sistema scarico. Gli altri nodi sono infatti in distacco per via del gioco.

screen

Procedendo con NEXT aumentano i livelli di carico e osservo che per incremento 3, ovvero al tempo 0.15 , e livello di carico 0.15 al quadrato per la pressione applicata, l’area di contatto si estende fino alla seconda fila di nodi.

screen

Con il crescere di carico, l’area di contatto aumento fino alla condizione in figura per incremento pari a 20.

Si ha un tipico esempio di contatto progressivo: il gioco ha un’influenza distaccante di valore fisso che si combina ad un carico che tende ad aumentare l’area di contatto. Tale area rappresenta l’equilibrio tra gioco e carico.

Siamo interessati ora alla distribuzione delle pressioni di contatto. Seleziono MORE > VECTOR > CONTACT NORMAL STRESS e porto su ON la visualizzazione dei vettori.

I vettori si plottano solo sui nodi in corrispondenza degli edges visibili e quindi solo su quelli di spigolo. Per visualizzare le pressioni di contatto su tutta la superficie e non solo sugli spigoli vado in POST ELEMENTS SETTINGS e cambio EDGES da OUTLINE A SURFACE. Infine REGEN.

Per aumentare la scala dei vettori vado in VECTOR PLOT > SETTINGS e porto in MANUAL la scala a 0.1.

Rilevo innanzitutto che le pressioni non sono massime in mezzeria per cui distribuzioni di contatto (alla \cos \theta o \cos^{2} \theta ) che prevedono forze massime sulla mezzeria non sono applicabili al piede di biella in trazione. Osservo inoltre che la pressione non è neanche uniforme in direzione assiale. Infatti in corrispondenza dell’indentazione si osserva che le tensioni sono più elevate per poi calare esponenzialmente all'aumentare della distanza da tale bordo. Siamo nel caso di una singolarità: indentatore a spigolo vivo su superficie elastica.

Per non avere a che fare con pressioni infinite si può smussare lo spigolo della boccola in lavorazione per ottenere uno spigolo arrotondato oppure aspettare che si usuri. Infatti, chiaramente con il tempo, i picchi di pressione agli estremi della boccola causeranno un’usura della superficie la quale recederà rispetto alla dimensione di alesaggio. Solo localmente allo spigolo i picchi di pressione tenderanno quindi a calare. Una valida alternativa consiste nel fare una lavorazione barellata della boccola, lavorazione più dettagliata ma anche più costosa. Invece di lavorare la superficie con l’alesatore e fare una superficie cilindrica viene leggermente barellata, si creano più giochi ai bordi invece che al centro e questo rende le pressioni di contatto più uniformi. L’usura in genere porta ad ottenere lo stesso risultato. Il problema in tal caso si avrebbe per quei motori che hanno vita troppo corta per usurarsi come, ad esempio, i motori della formula 1.

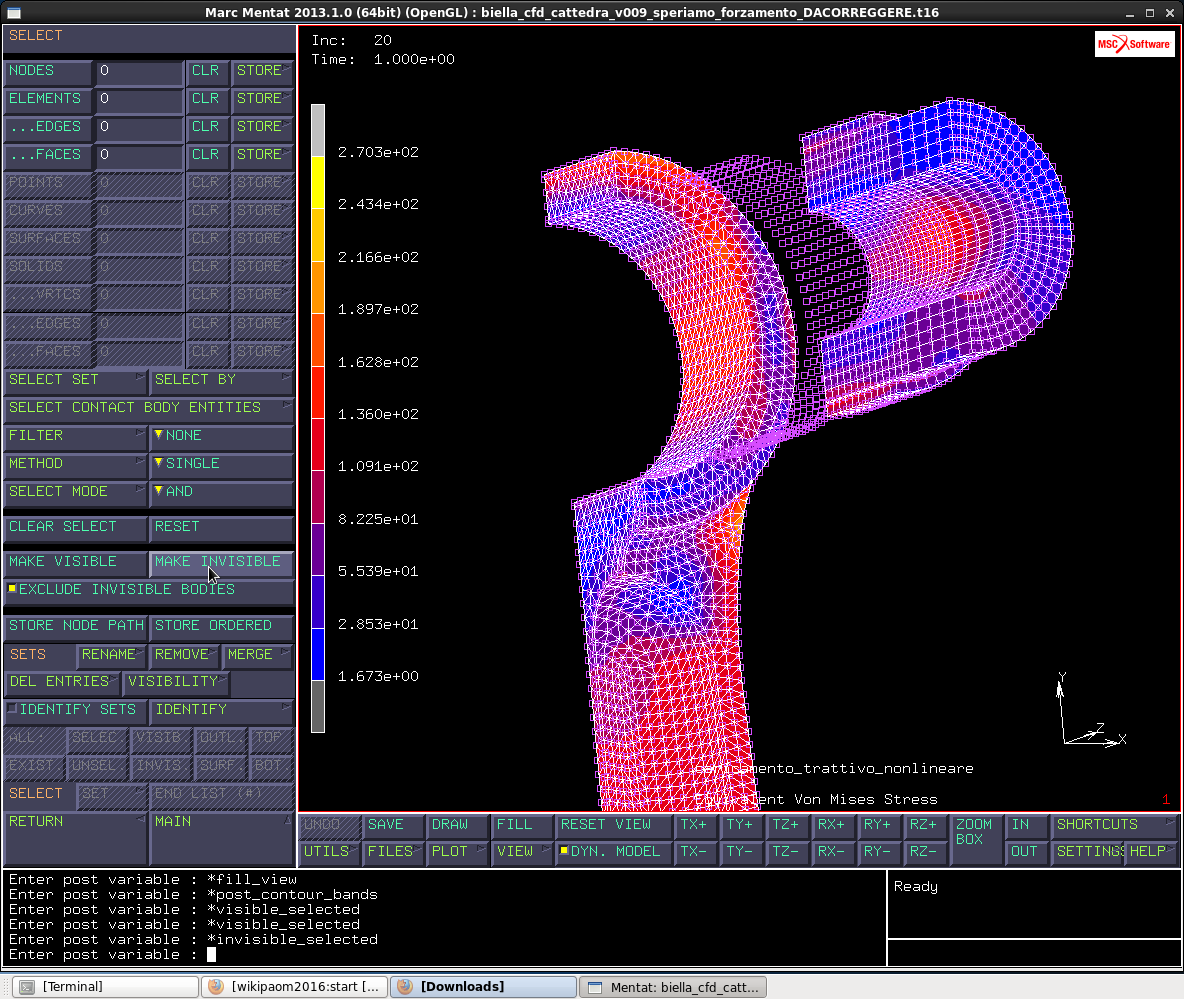
Visualizziamo ora lo stato tensionale del piede di biella: vado in SELECT > VISIBILITY e seleziono per il piede ALL, boccola NONE ,spinotto NONE.

Plottiamo le equivalent Von Mises Stress sul piede di biella quindi da SCALAR PLOT selezioniamo come SCALAR le EQUIVALENT VON MISES STRESS. Ricordiamo che le Von Mises Stress, in termini di singoli componenti, non sono lineari. Si combina lo stato tensionale del solo forzamento con la trazione.

Il calcolo in compressione risulta lo stesso di quello in trazione con le seguenti correzioni: le forze saranno applicate sui nodi inferiori anziché quelli superiori del piede di biella e considerati 32 KN compressivi invece di 14 KN trattivi, come indicato dalla traccia. Dalla condizione forzamento+trazione e forzamento+compressione si ottiene poi un ciclo di fatica per ogni punto del piede. La valutazione del ciclo si effettua via resistenza.

Ricordiamo che il calcolo in trazione è stato fatto in condizioni di aderenza. Per verificarle innanzitutto visualizziamo tutti gli oggetti di lavoro: SELECT > MAKE INVISIBLE. Non avendo selezionato nessun elemento appariranno tutti le parti.

Per quanto riguarda i nodi ausiliari ricordiamo che le reazioni vincolari su tali nodi non sono altro che le azioni scambiate nodo per nodo sull’interfaccia bronzina-piede. In tal caso non abbiamo singolarità tensoriale perché le due superfici sono allineate ed il materiale è omogeneo. Monitoriamo quindi questo stato tensionale.

Innanzitutto passiamo al sistema in coordinate cilindriche quindi da POST PROCESSING RESULTS in SCALAR PLOT SETTINGS, cliccare sulla voce RESULTS COORDINATE SYSTEM ed attivare CYLININDRICAL. Di default si ha come asse cilindrico l’asse z.

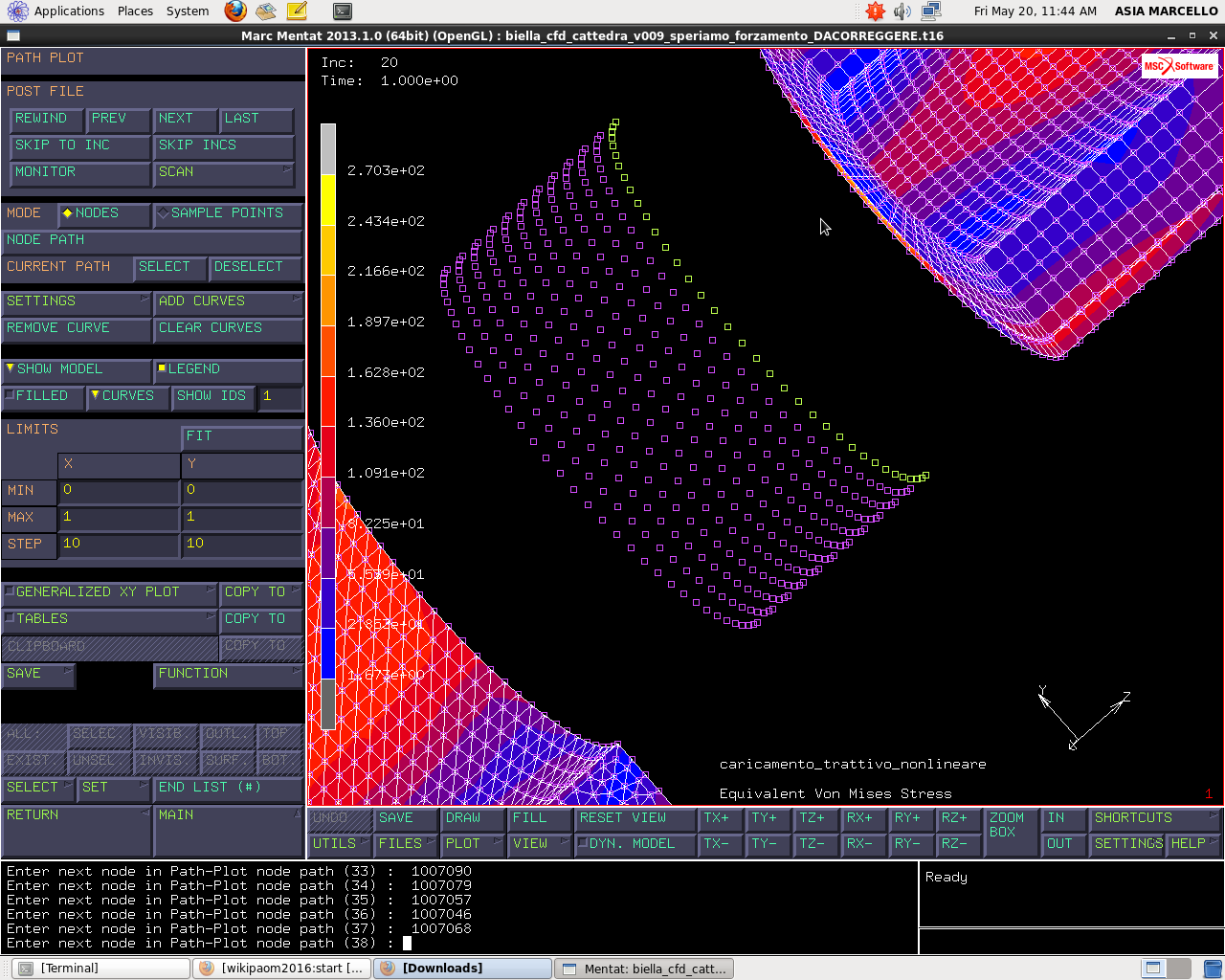
Vado in PATH PLOT, funzione che permette di fare grafici su una linea di nodi. Realizziamo ora grafici solo sulla linea di nodi di nostro interesse: POST PROCESSING RESULTS > PATH PLOT > NODE PATH e seleziono la prima fila di nodi ausiliari come in figura.

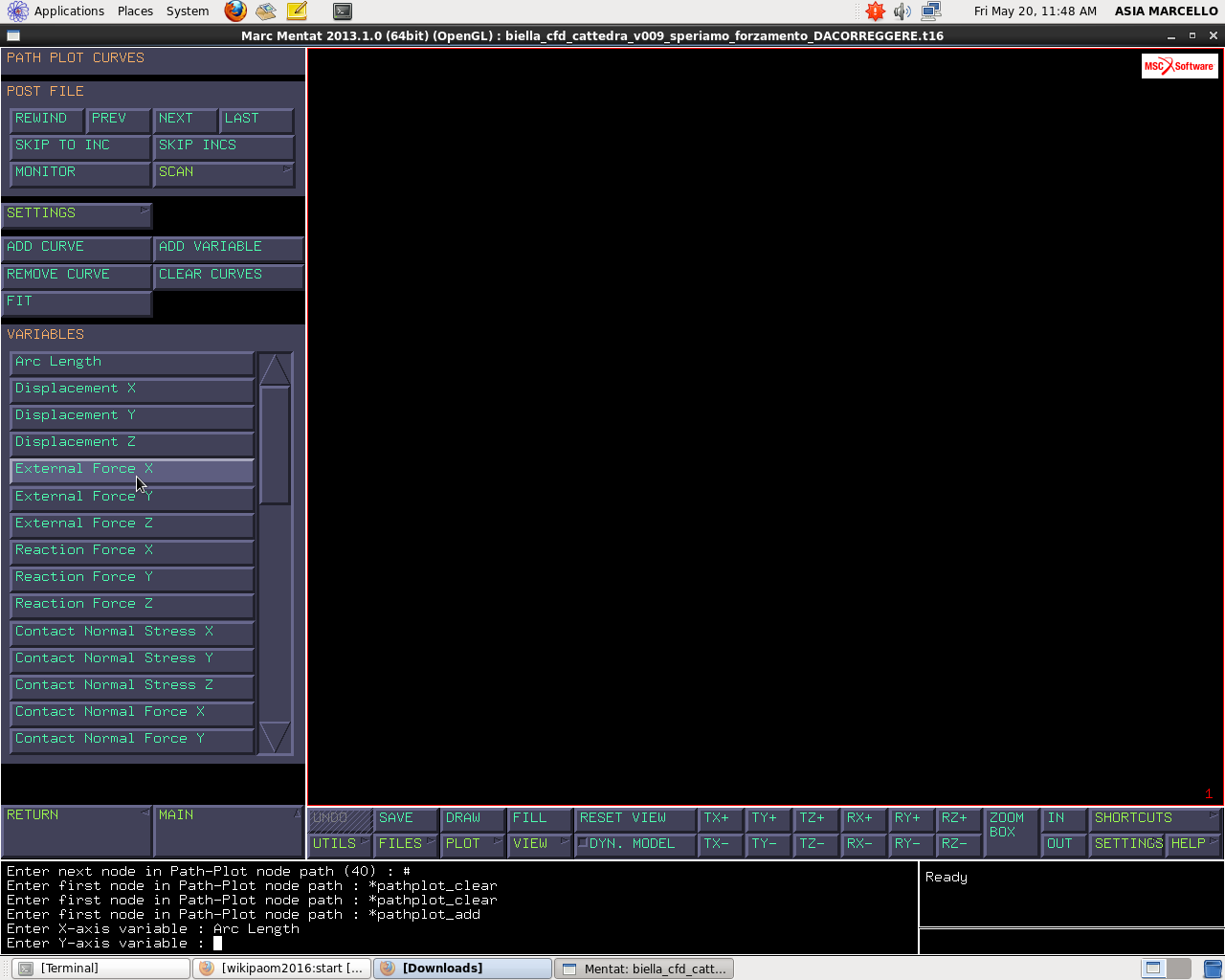
In questo modo definisco un percorso lungo i nodi di campionamento. A questo punto do il fine lista e lungo tale percorso plotto delle curve.Seleziono quindi ADD CURVES ed inserisco per la prima curva come variabile x ARC LENGHT, come variabile y REACTION FORCE X che in coordinate cilindriche rappresenta la radiale.

Per la seconda curva come variabile x ARC LENGHT, come variabile y REACTION FORCE Y che in coordinate cilindriche rappresenta la circonferenziale. Infine pe la terza come variabile x ARC LENGHT, come variabile y REACTION FORCE Z che in coordinate cilindriche rappresenta quella assiale.

Per quanto riguarda la convenzione dei segni, quando la reazione è positiva sotto carico risulta compressiva. In figura le curve gialle rappresentano le azioni assiali, le rosse le azioni circonferenziali, le verdi le azioni radiali che agiscono tra boccola e piede di biella sullo spigolo punto per punto.

In tutti i punti, esclusi primo e ultimo perché influenzati dalla simmetria, ho una forza normale e due tangenziali. Considero la radice della somma dei quadrati delle due forze tangenziali e affinché ci sia aderenza devo confrontare questo valore con il prodotto della forza normale per il coefficiente di attrito. Se il valore calcolato risultasse minore del prodotto, l’ipotesi di aderenza sarebbe effettivamente verificata. In alcuni punti, ad esempio in grande quantità sullo spigolo tra bronzina e piede la forza normale è trattiva quindi sembrerebbe non essere una condizione fisica. Ricordiamo tuttavia che bisogna aggiungere al caricamento trattivo il contributo dovuto all’interferenza. L’interferenza per come è stata costruita cioè senza attrito darà azioni tangenziali nulle e azione normale compressiva.

Salviamo il modello ottenuto e apriamo un nuovo foglio di lavoro: FILES > NEW

La molla elicoidale da modellare presenta le seguenti caratteristiche:

• raggio medio avvolgimento 20 mm;
• passo 15 mm;
• filo cavo de=12 mm, di=6 mm;
• in titanio (E=110000 MPa, nu=0.3, rho=4.7e-9 tonn/mm^3);
• 4.5 spire.

Ripassiamo innanzitutto al sistema in coordinate cartesiane seguendo le indicazioni fornite precedentemente.

Aggiungo un punto nell’origine degli assi: MESH GENERATION > POINTS ADD ed inserisco le coordinate 0, 0 ,0. Secondo le caratteristiche della molla, questa terminerà ad una distanza di 4.5 dall’origine. Inserisco un secondo punto di coordinate 0, 0, 4.5*15 essendo 15 il numero di avvolgimenti.

RESET VIEW > FILL: la molla si estende lungo z.

Creo ora il nodo sulla spira: NODES > ADD e fornisco le coordinate 20, 0, 0.

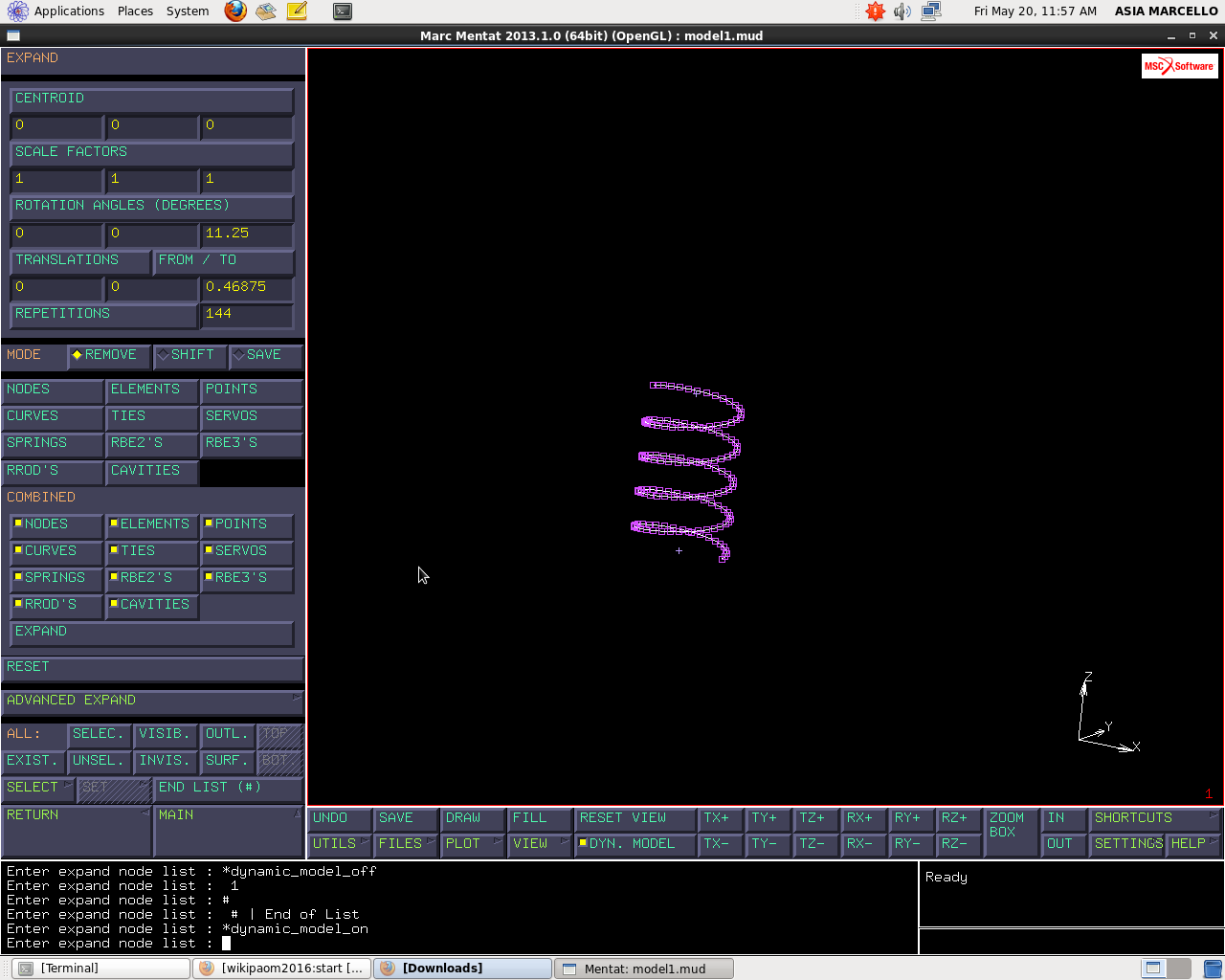
Procedo estrudendo il nodo fino ad ottenere la molla: da MESH GENERATION, seleziono EXPAND e modifico i valori di ROTAZIONE e TRASLAZIONE:

La rotazione avviene intorno all’asse z con passo pari a 360/32 in quanto voglio 32 passi circonferenziali.

La traslazione avviene assialmente quindi si modifica la cordinata z in 15/32 pari al passo sul giro fratto il numero di incrementi.

Si inseriscono un numero di ripetizioni pari a 32*4.5.

Selezionare NODES e cliccare sul nodo definito.

Per eliminare le ripetizioni selezionare SWEEP nel menu MESH GENERATION e applicare a tutti gli elementi lasciando la tolleranza di default.

Prima di inserire proprietà geometriche generiamo due nodi che fungeranno da nodi di controllo una volta definite le rbe2 opportune. In MESH GENERATION selezionare NODES > ADD e cliccare sui due punti definiti inizialmente.

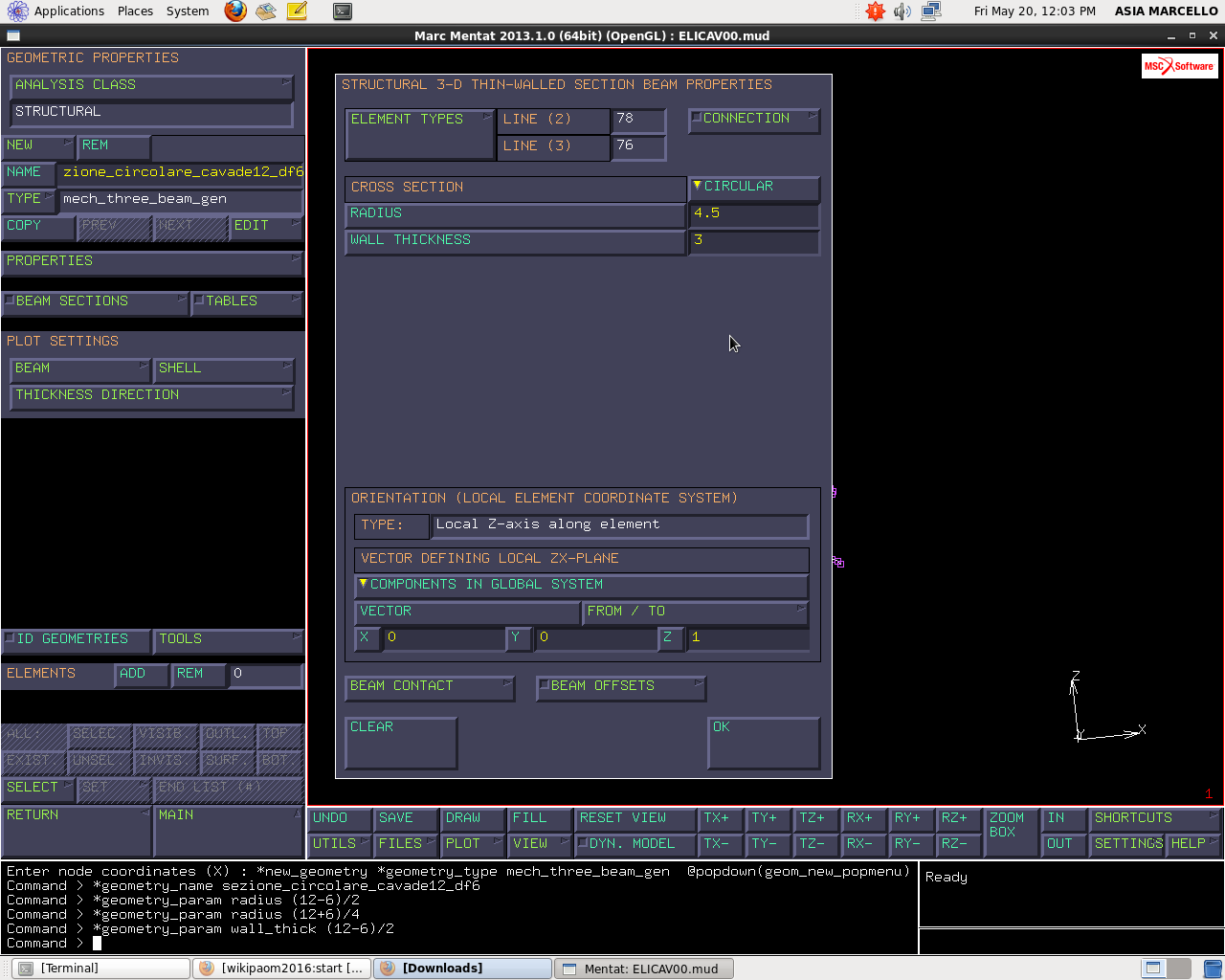
Definiamo ora la proprietà geometrica che descrive la sezione della trave: GEOMETRIC PROPERTIES > NEW > STRUCTURAL > 3D.

Per gli elementi trave si hanno diverse opzioni:

• TRUSS: è il puntone tirante che lavora solo su sforzo normale. Al fine di lavorare solo su sforzo normale ha integrate due cerniere sferiche in testa e coda, quindi ad un truss non è possibile trasmettere rotazione, inoltre non si posizionano mai due truss di fila. Le strutture fatte in truss devono essere perfettamente triangolarizzate sul piano e tetraedrizzate nello spazio, altrimenti sono labili.
• SOLID SECTION BEAM: permette di definire una trave a sezione piena.
• Nel nostro caso la trave è una THIN-WALLED SECTION BEAM, trave a sezione sottile che può aperta o chiusa. Nel caso specifico chiusa.

Rinominiamo con “sezione_circolare_cava_de12_di6”.

Si accede ora al menu PROPERTIES. La sezione può essere del tipo circolare o generale. Se generale devo disegnare un cad specifico delle sezioni dal menu BEAM SECTION. Quella di default è già implementata. Per la sezione circolare basta fornire un raggio medio e spessore di parete. Nel nostro caso la sezione è CIRCOLARE quindi in corrispondenza di RADIUS si inserisce (12+6)/4, in corrispondenza di WALLED THICKNESS (12-6)/2.

Se la sezione fosse ellittica bisognerebbe specificare l’orientazione nello spazio del semiasse maggiore con LOCAL ASSES. Questo dovrebbe essere ortogonale all’asse baricentrico, se non lo è il software lo renderà ortogonale tramite ortogonalizzazione di Gram-Schmidt ovvero sottraendo la componente ortogonale all’asse. Nel caso di sezione circolare non è importante fornire l’orientazione della sezione. L’unico caso errato sarebbe quello di un vettore parallelo all’asse baricentrico. L’asse da default è parallelo all’asse z, nel caso specifico quindi va bene.

Applico questa proprietà a tutti gli elementi: ELEMENTS> ADD > ALL EXIST.

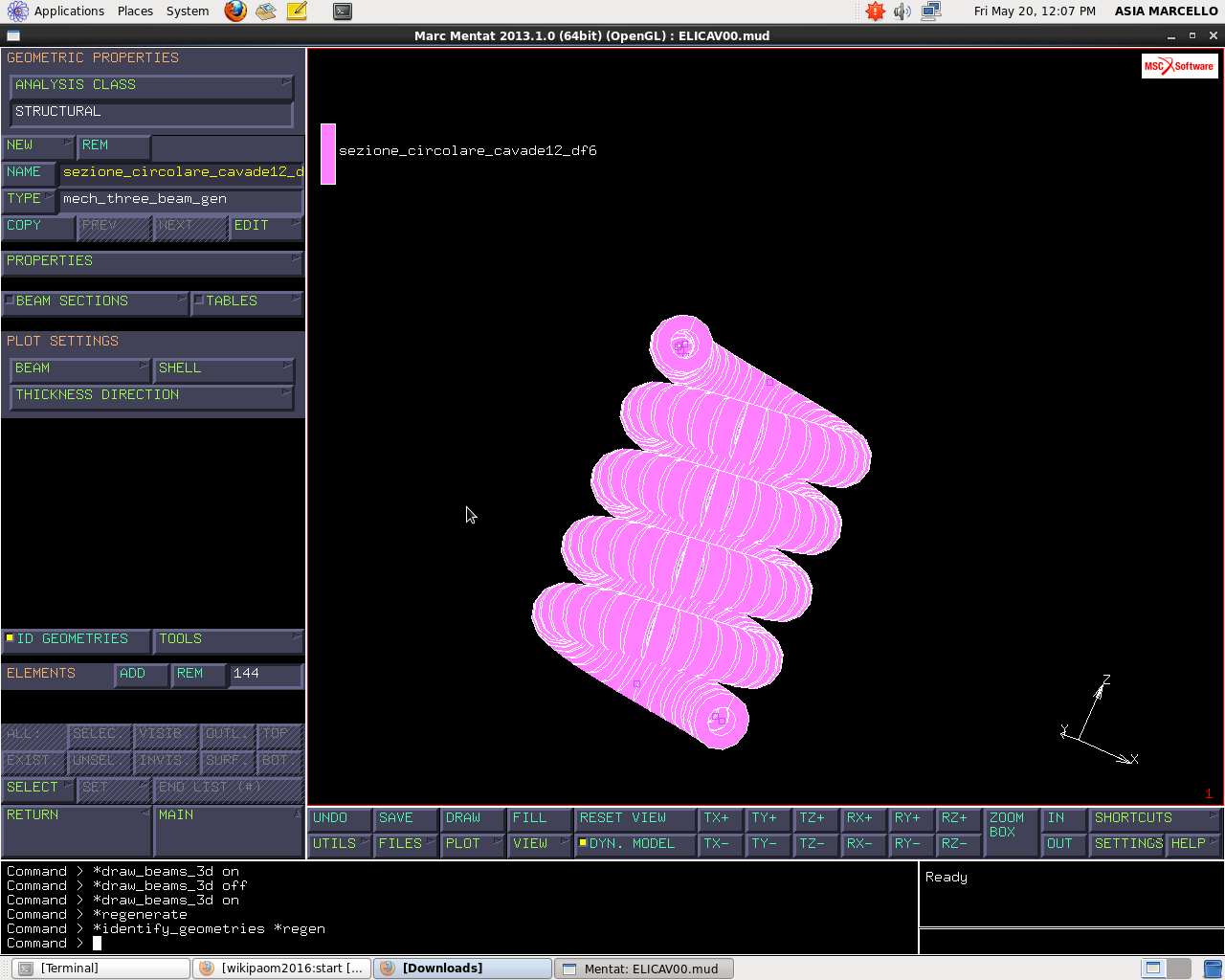
Se siamo interessati all’effetto che si ottiene plottando effettivamente la sezione di trave attorno al filo andiamo in PLOT SETTINGS > BEAM > PLOT BEAMS IN 3-D > REGEN.

Tornare ora alla configurazione iniziale e aggiungere il materiale. Dal MAIN MENU selezionare MATERIAL PROPETIES > NEW > STANDARD > rinominare “titanio”. In GENERAL aggiungere una densità di 4.7e-09, densità intermedia tra alluminio ed acciaio. In STRUCTURAL inserire un modulo di Young di 11000 e un coefficiente di Poisson di 0.3. Applicare la proprietà a tutti gli elementi: ELEMENTS > ADD > ALL EXIST.

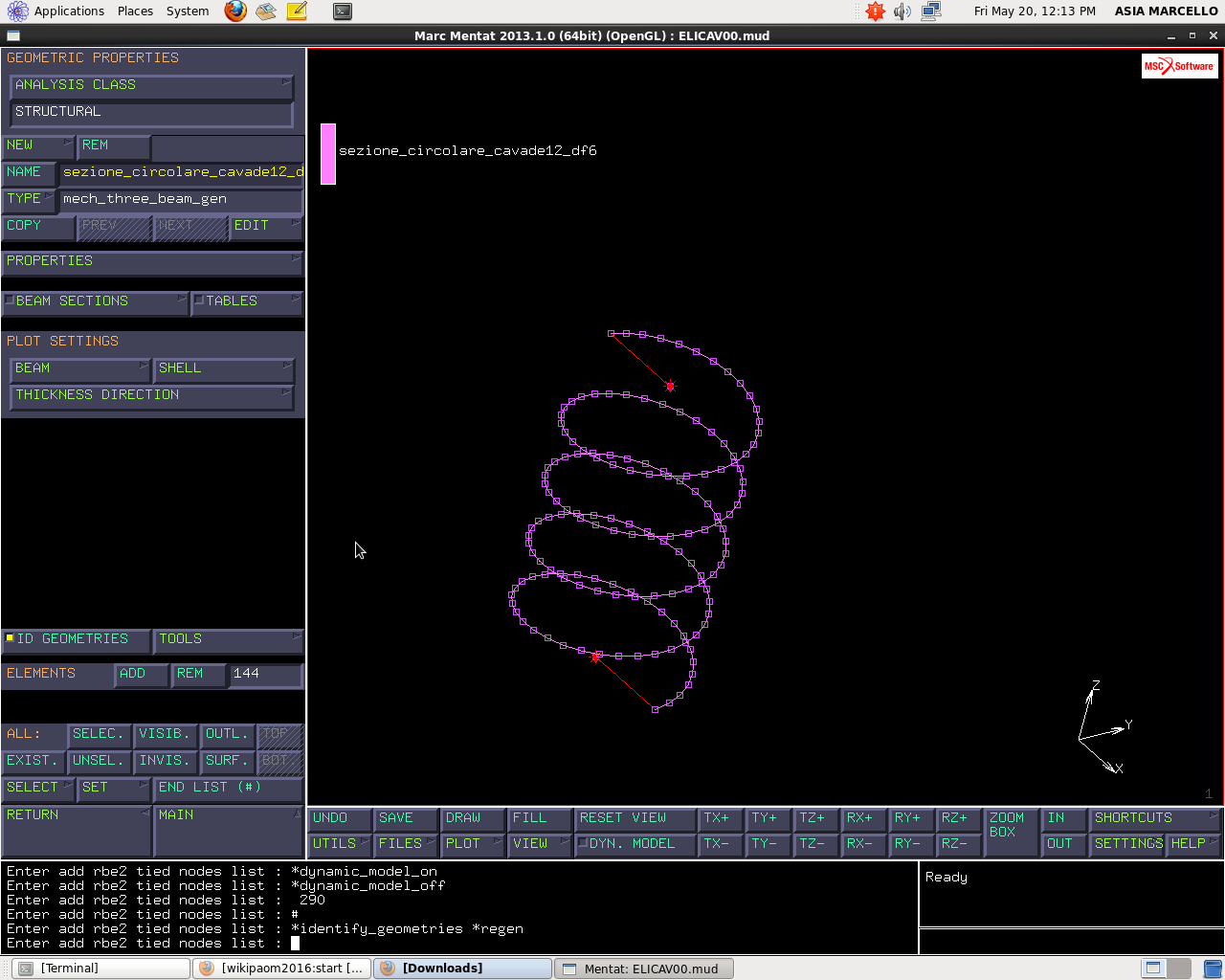
Si inseriscono ora due vincoli di tipo RBE2.

Procediamo in questo modo: LINKS > RBE2’S > NEW > NODE e selezioniamo uno dei due nodi liberi. Aggiungere poi come TIE NODE il nodo di estremità della molla e selezionare tutti i sei gradi di libertà. In questo modo il nodo è incastrato e quindi la molla incernierata. Si crea un rbe2 analogo: NEW > NODE, selezioniamo il nodo libero. Selezionare poi come TIE NODE l’altro estremo della molla, selezionare tutti i sei gradi di libertà e dare il fine lista.

Il modello manca ancora di vincolamento tuttavia posso già estrarre i modi propri della molla libera.

Dal MAIN MENU > LOADCASES > NEW e scegliere la tipologia di loadcase. Il DYNAMIC MODAL consente l’estrazione di modi e frequenze proprie. Il DYNAMIC TRANSIENT calcola le evoluzioni da condizioni inerziali. Il DYNAMIC HARMONIC calcola la risposta armonica.

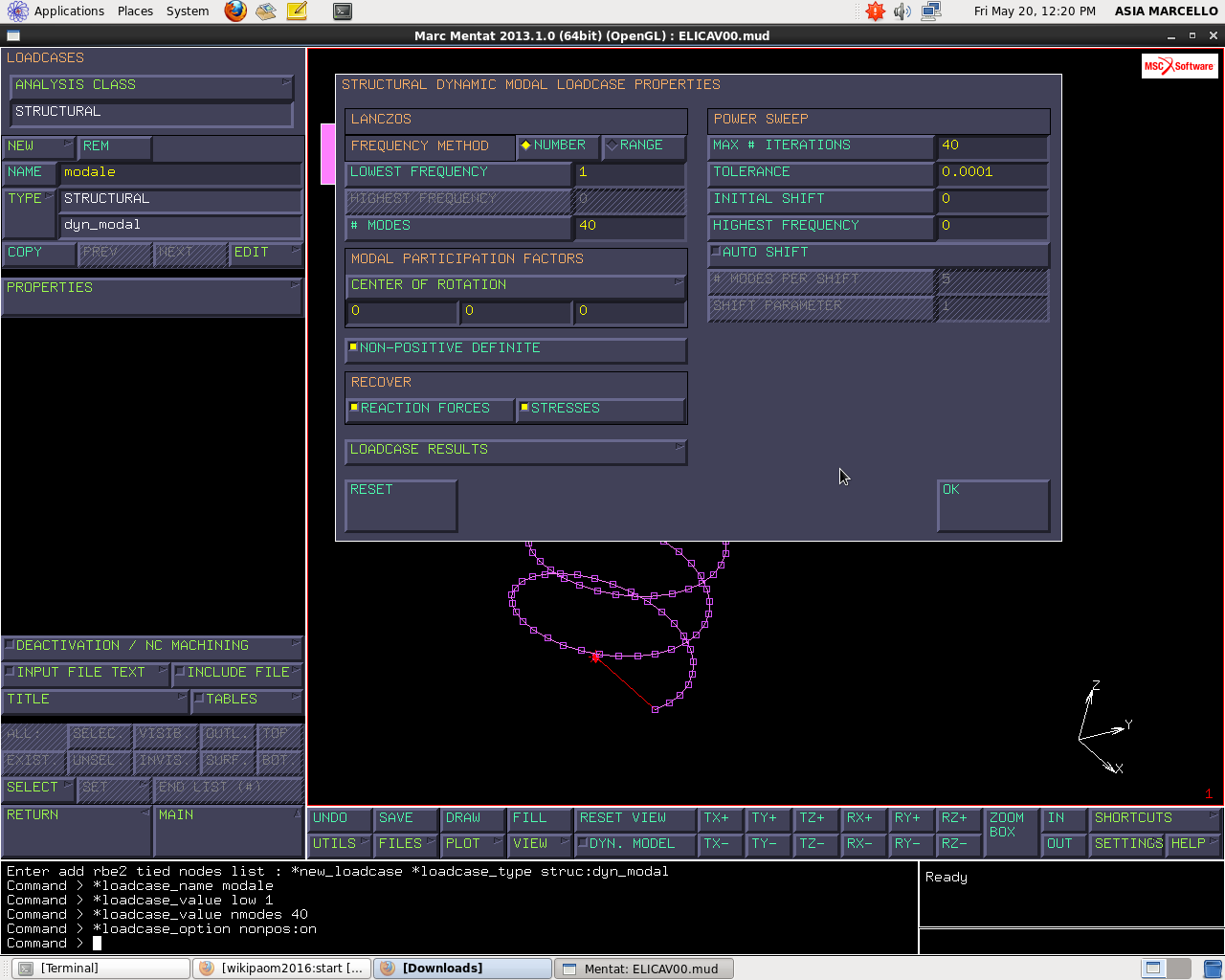
Scelgo il DYNAMIC MODAL e rinomino in “modale”.

Il menu delle PROPERTIES è diviso in due parti: LANCZOS e POWER SWEEP. Questi sono sostanzialmente algoritmi per calcolo numerico per estrarre valori e autovettori quando abbiamo più gradi di libertà. Di default si usa iL LANCZOS. Tuttavia questo algoritmo iterativo presenta difficoltà in presenza di autovalori multipli. L’algoritmo POWER SWEEP risulta più robusto ma lento.

Se si lascia il LANCZOS il sistema restituisce i primi dieci modi propri a frequenza crescente a partire da frequenza minima 0 Hz. Tuttavia frequenza minima 0 Hz significa che ci sono modi di corpo rigido se il sistema non è vincolato. I modi di corpo rigido sono tutti autovalori nulli cioè multipli, quindi l’algoritmo potrebbe dare problemi. Per evitare questa problematica si prende come frequenza minima 1 Hz. Tipicamente questa è una soglia per cui è facile non ci siano modi propri per un componente meccanico.

Per il caso si richiedono i 40 modi propri sopra 1 Hz.

La funzione NON-POSITIVE DEFINITE assicura che il sistema sia labile. Quindi selezioniamo questa funzione se sappiamo a priori che il sistema lascia liberi i moti di corpo rigido. Nel nostro caso si sa che i vincoli sono incompleti e quindi il sistema non è definito positivo.

Si procede a questo punto con il JOB.

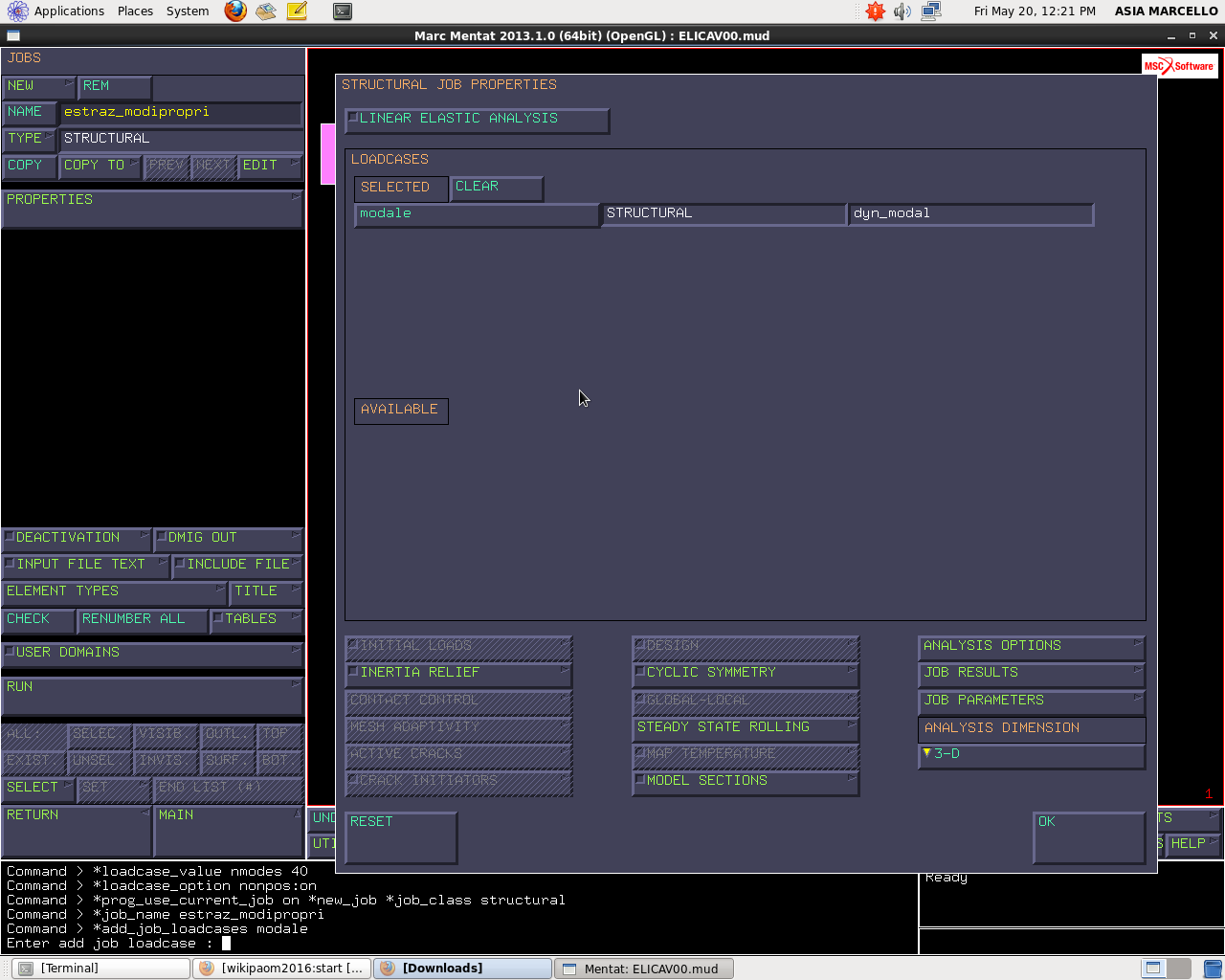
Creo un nuovo JOB di tipo STRUTTURALE e lo chiamo “estraz_modipropri”. Non essendoci dei vincoli, non è possibile attivare alcun tipo di INITIAL LOADS, però, se bisogna inserire dei vincoli è importante ricordare di inserirli in initial load. I vincoli all’istante 0 sono quelli che entrano nella matrice di rigidezza, utilizzata per estrarre autovalori e autovettori che sono i modi a frequenza propria.

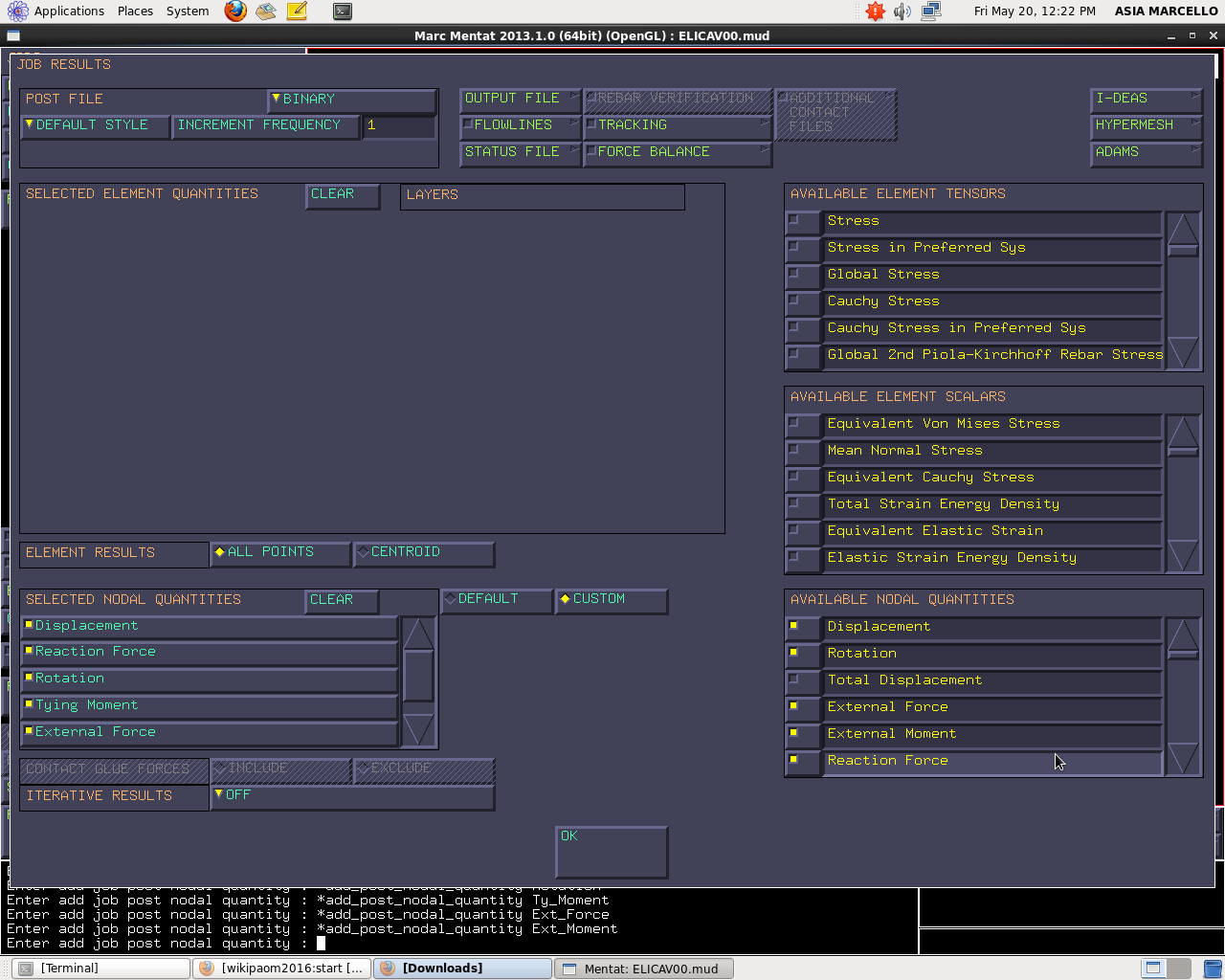
Entro in JOBS RESULTS e seleziono come NODAL QUANTITIES: displacement, rotation, reaction force, external force, external moment, tying force e tying moment.

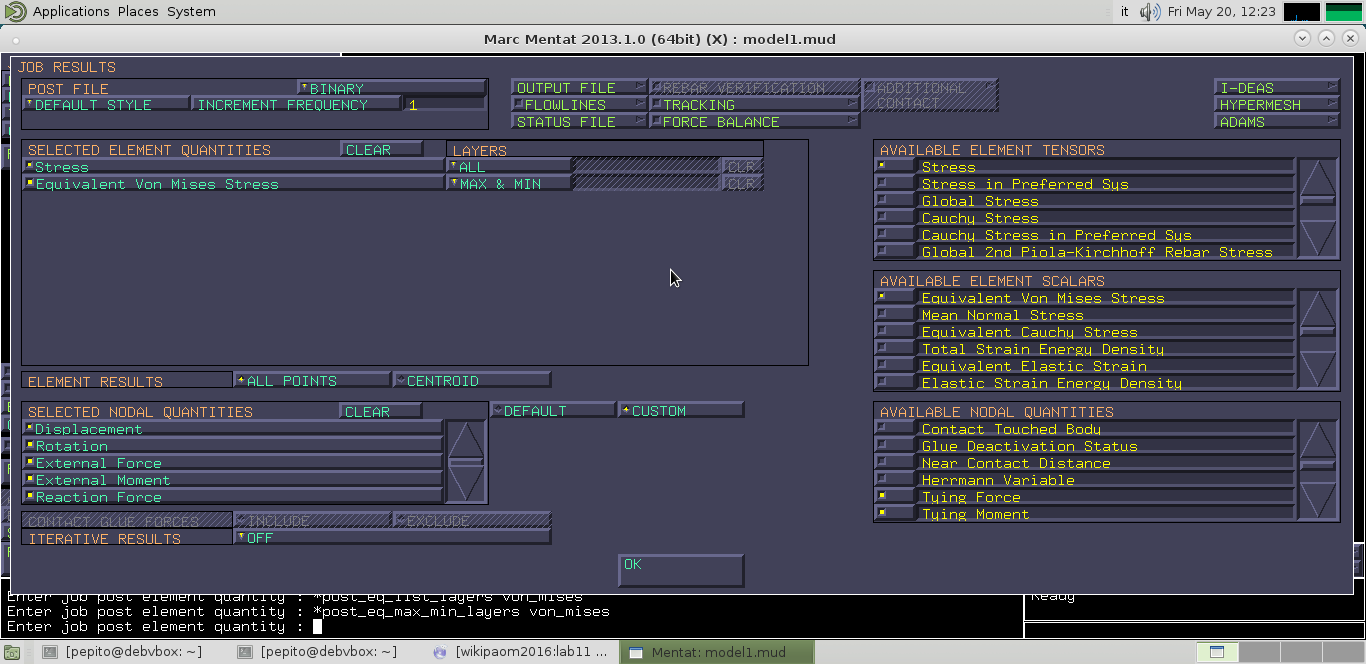
Aggiungo, in ELEMENT QUANTITIES, “Stress” a tutti i layer ed “Equivalent Von Mises Stress” al MAX&MIN della stratificazione implicita dell’elemento.

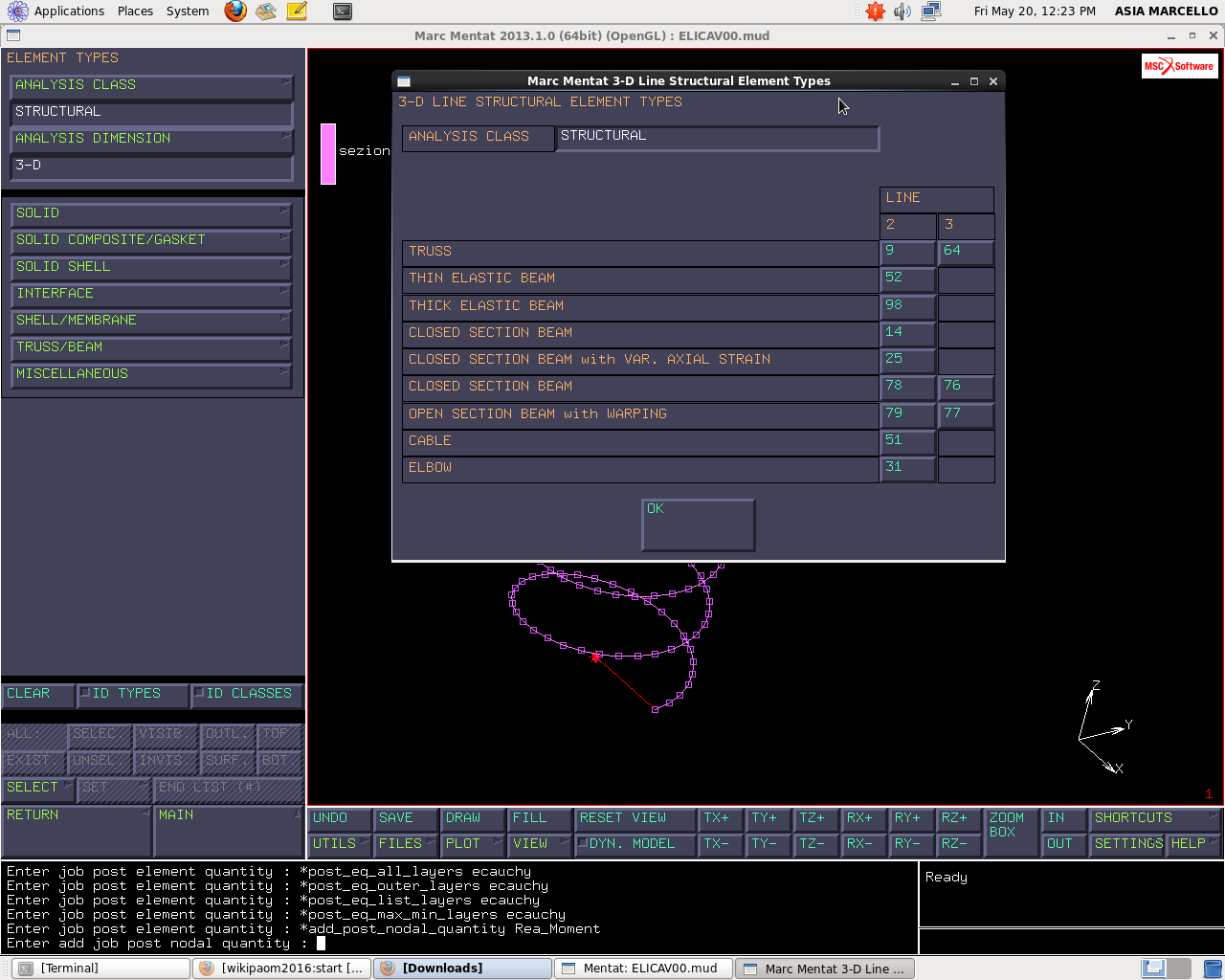
Devo stabilire l’elemento che sarà prescelto per modellare queste travi. Vado, dal menu JOBS, in ELEMENT TYPES>TRUSS/BEAM>CLOSED SECTION BEAM (elemento 14) e lo applico a tutti gli elementi che esistono. Per conoscere le caratteristiche dell’elemento 14, vado in HELP>VOLUME B: ELEMENT LIBRARY dove è spiegato che i Layer sull’elemento trave sono i punti di campionamento dello stato tensionale lungo la parete.

Possono essere inserite anche delle masse ed inerzie concentrate andando in INITIAL CONDITIONS>NEW>POINT MASS. Verranno richiesti i valori delle masse lungo le tre direzioni principali insieme a tre momenti di inerzia che sono quelli calcolati rispetto agli assi principali di inerzia altrimenti, se così non fosse, andrebbero calcolati anche i momenti misti per un totale di sei momenti, e sarebbe molto più complicato; perciò, quando sono richiesti tre momenti, implicitamente, sono riferiti agli assi principali d’inerzia. Nel nostro caso non andremo ad inserire nessuna massa concentrata.

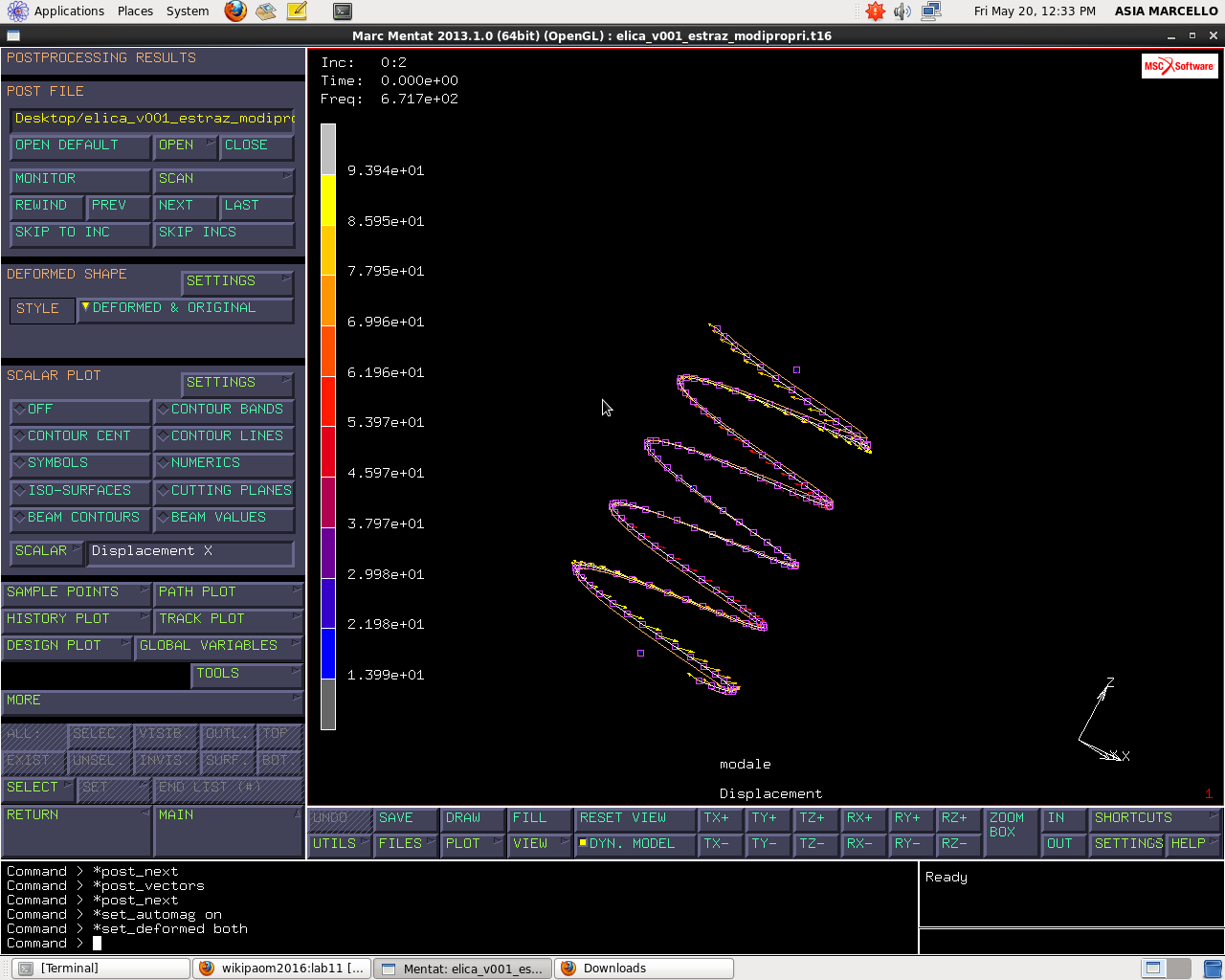
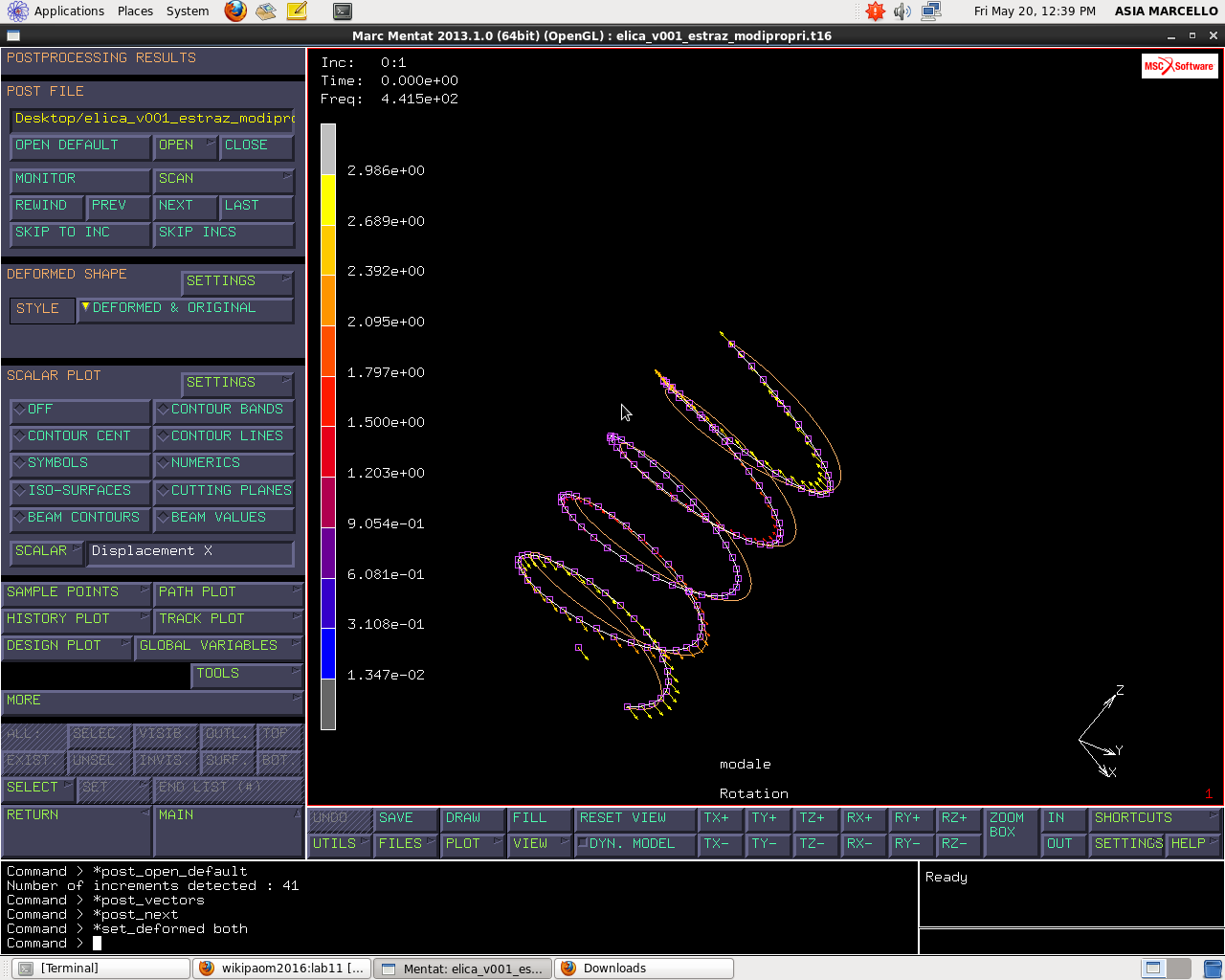
Andiamo nel menu JOBS>RUN>SUBMIT. Con questo calcolo vengono estratti i primi 40 modi propri della struttura. Apriamo il file dei risultati. L’incremento 0 è scarico quindi non ci interessa. Passiamo all’incremento successivo con NEXT che sarà l’incremento 0:1, cioè il sotto incremento 1 dell’incremento 0, chiamato così perché utilizzo la matrice di rigidezza e di massa dell’incremento 0 per estrarre il modo proprio 1. La frequenza è pari a 571 Hz. Il modo proprio è visualizzato in scala unitaria però, essendo un autovettore, la scala è arbitraria per definizione. Marc li scala a massa modale unitaria. Il modo 1 è un modo di libera estensione della molla, quindi conviene guardare gli spostamenti. MORE e attiviamo VECTOR DISPLACEMENT. Osserviamo che si tratta di un modo di espansione.

Il modo proprio successivo (2) è a frequenza 671 Hz e si tratta di un modo proprio in cui gli estremi controruotano.

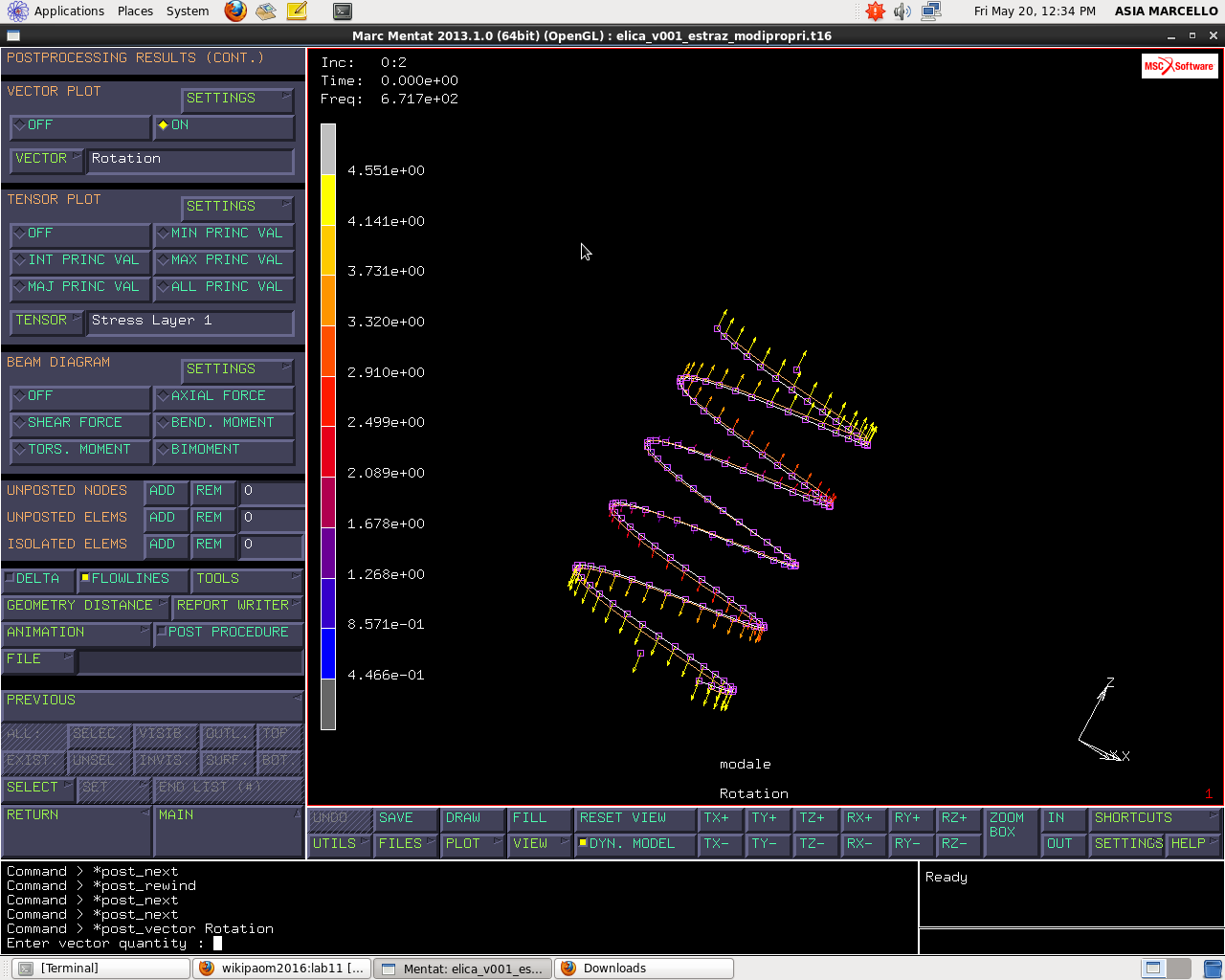
Il modo proprio 3 è di tipo flessionale. Andando avanti con gli altri modi la frequenza è via via crescente. Finora abbiamo visualizzato solo gli spostamenti, se seleziono, invece, le rotazioni andrò a visualizzare i vettori di rotazione come in figura:

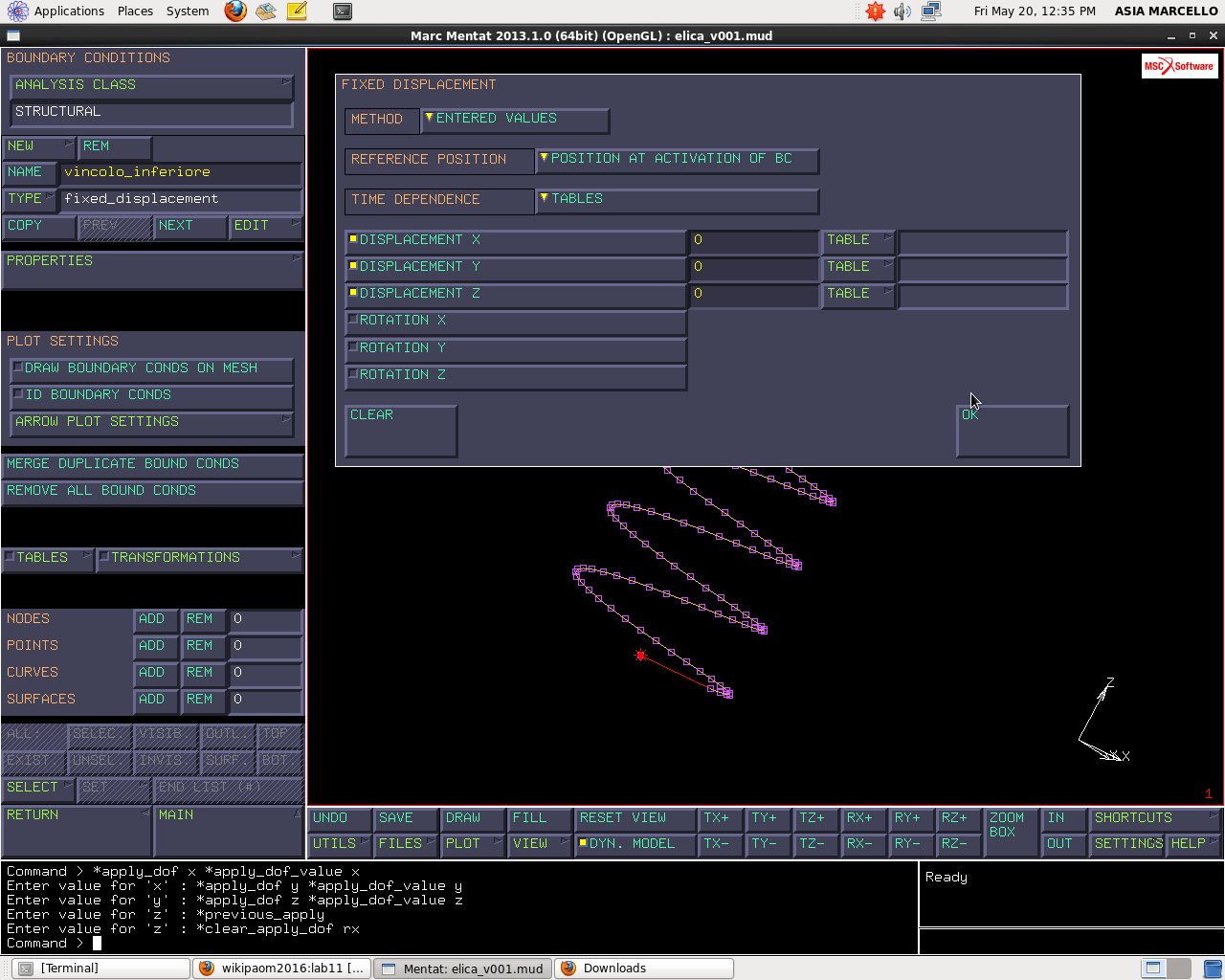
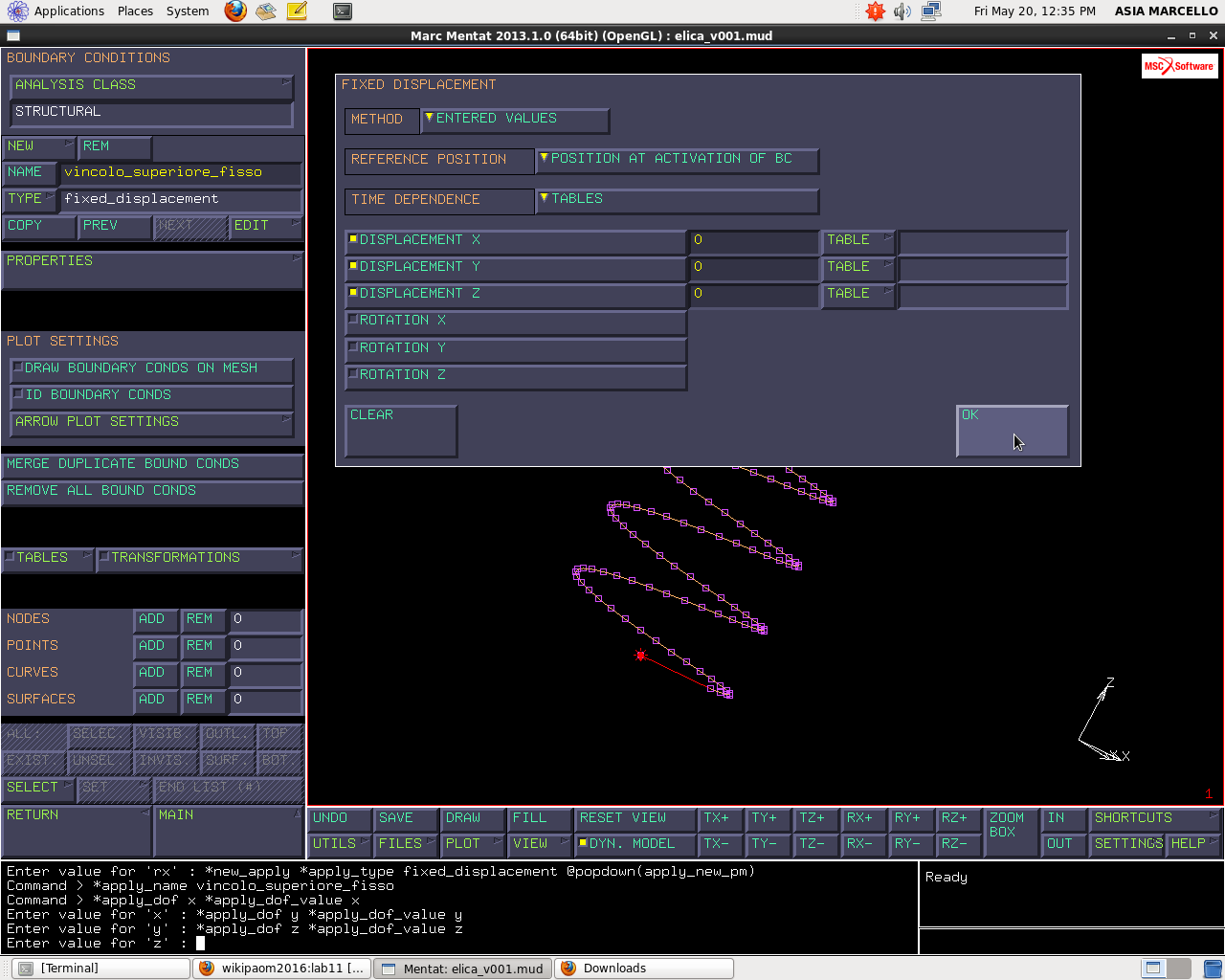
Questi sono i modi della molla libera, ora provo a cambiare sistema di vincolamento. BOUNDARY CONDITIONS>NEW>STRUCTURAL>FIXED DISPLACEMENT e lo chiamo “vincolo_inferiore”. Lo applico al nodo più in basso lungo z e impongo le condizioni in figura.

Aggiungo un altro vincolo che chiamo “vincolo_superiore_fisso” e lo applico al nodo superiore lungo z con le stesse proprietà dell’altro, in modo da avere ai due estremi dei giunti sferici.

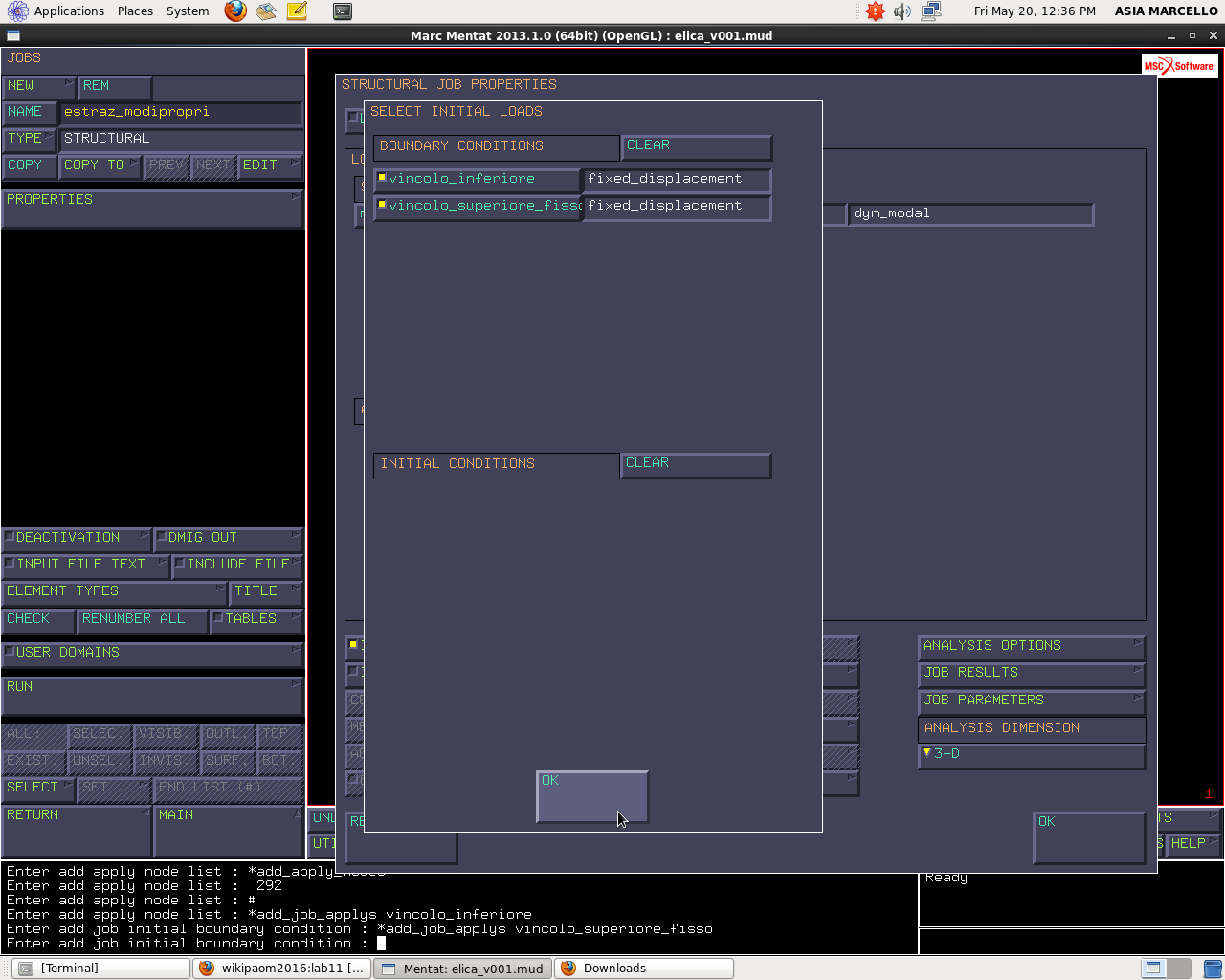
Il sistema, a questo punto, ha ancora una labilità, cioè può ruotare attorno al proprio asse. Torno nel menu JOBS>PROPERTIES e osservo che sono state attivate le INITIAL LOADS perché ora ho dei vincoli. Quindi entro e clicco sui vincoli per attivarli.

Ripeto il calcolo nelle nuove condizioni imposte, quindi RUN>SUBMIT. Estraggo i modi e le frequenze proprie non più con la struttura libera ma con la struttura ad estremità vincolate e rotazione libera. Apro il file dei risultati e osservo il primo modo proprio in cui la molla deforma sul fianco. Osservazione: la frequenza risulta essere più bassa rispetto al caso di corpo libero ma, in realtà, a volte, il sistema non vincolato ha frequenze proprie più alte rispetto al sistema vincolato se trascuro i moti di corpo rigido.

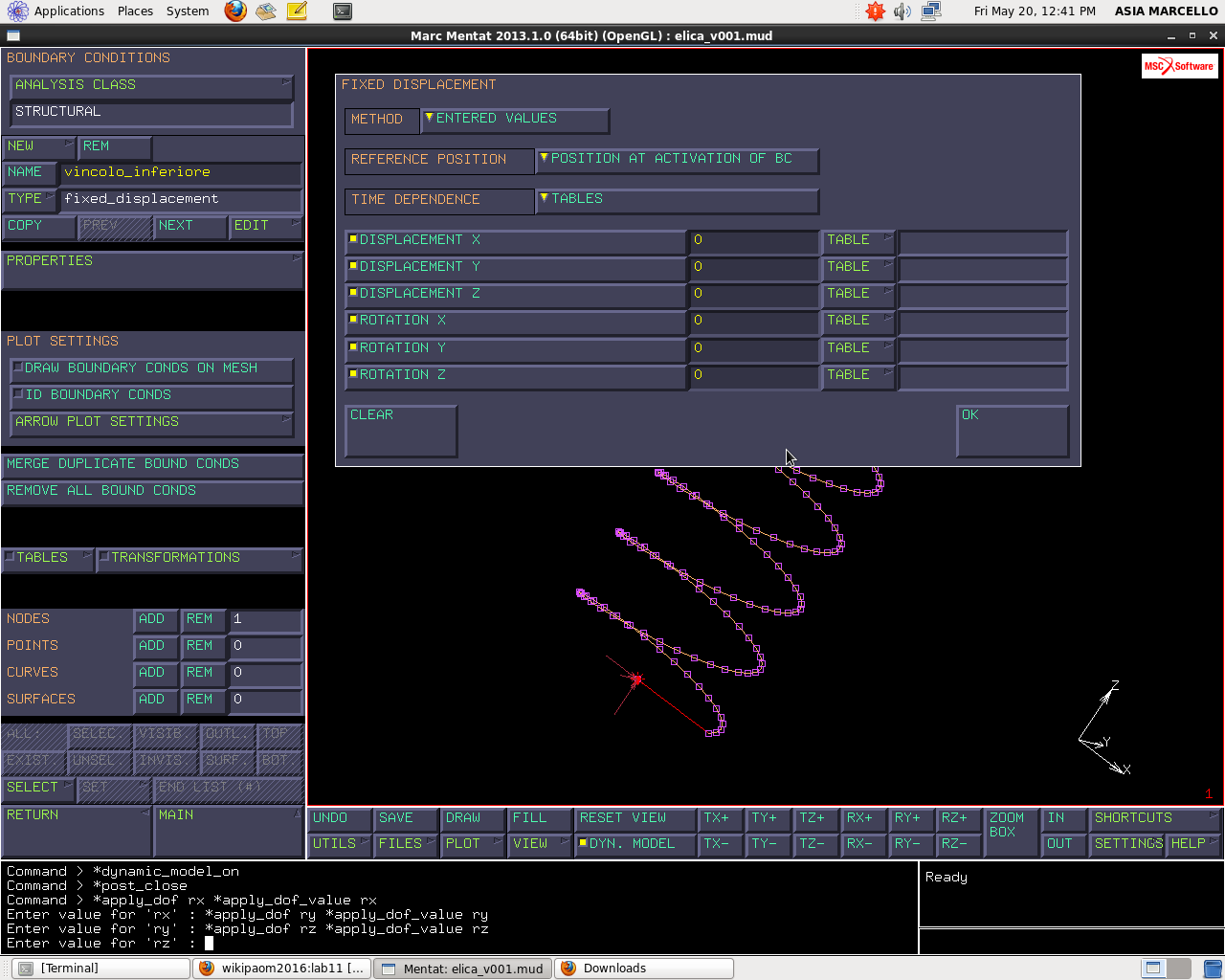
Immagino che la molla sia una molla di compressione che lavora tra due piani che non la lasciano libera di ruotare alle estremità, quindi, i due vincoli che ho messo come giunti sferici li modifico in due incastri. BOUNDARY CONDITIONS>”vincolo_inferiore”>PROPERTIES e attivo le rotazioni. La stessa modifica la devo fare anche per il “vincolo_superiore_fisso”.

Controllo in JOBS che ci siano i due incastri selezionati nelle INITIAL LOADS e lancio di nuovo il calcolo, RUN>SUBMIT. Apro il file dei risultati e vedo che la prima frequenza propria a estremi incastrati vale 590.1 Hz. Nel secondo modo la frequenza vale 643.4 Hz, nel terzo 732.6 Hz e nei successivi è sempre crescente.

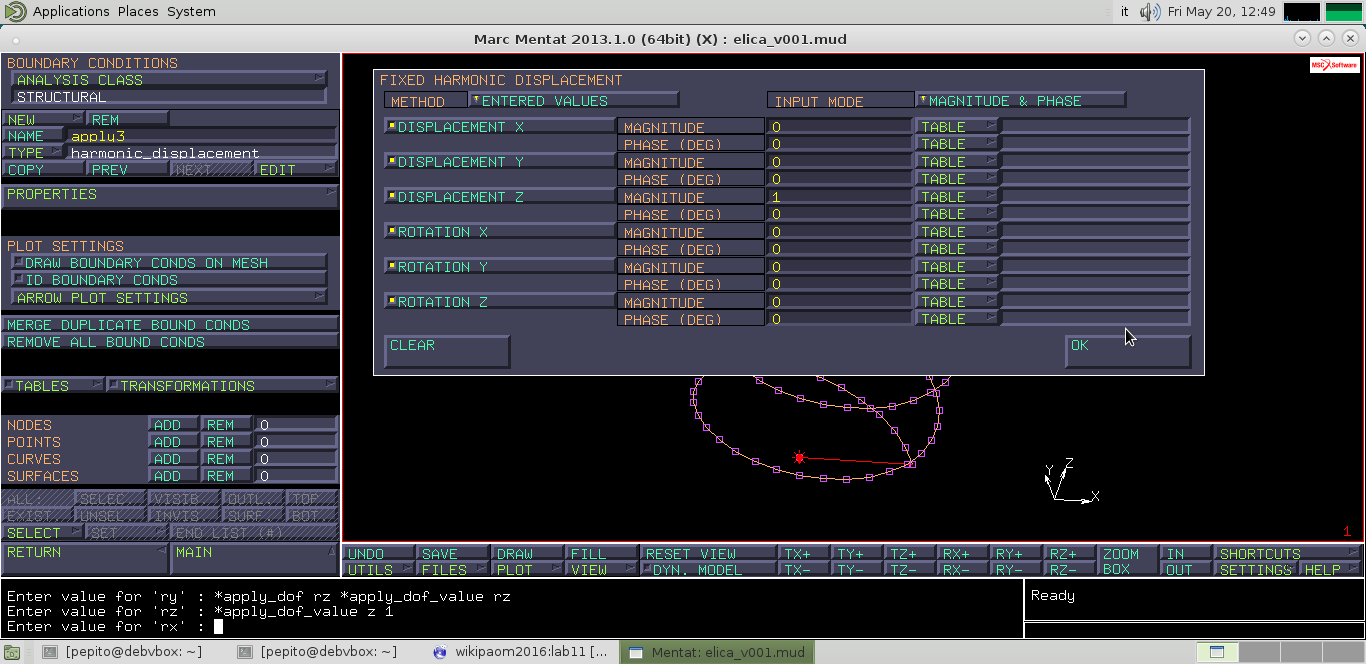
Per eccitare la molla, fisso la base superiore e faccio oscillare la parte inferiore. Creo una BOUNDARY CONDITION di tipo STRUCTURAL>FIXED HARMONIC DISPLACEMENT, che si tratta di uno spostamento imposto, modulato armonicamente nel tempo. Lo chiamo “vincolo_superiore_mobile” in contrasto con quello fisso precedente. Seleziono le proprietà in modo da avere spostamenti e rotazioni imposti in modulo e fase, ovvero in parte reale (modulata per cosΩt) e parte immaginaria (modulata per -senΩt). Impongo spostamento z con fase 0 e magnitudo 1. Non fornisco la frequenza che inserirò nel loadcase. Applico vincolo all’estremo superiore con NODES>ADD. Adesso la molla, armonicamente, va su e giù di 1mm.

Vado in LOADCASES>NEW>DYNAMIC HARMONICS, risposta a sollecitazione armonica, che chiamo “risposta_in_frequenza”. Voglio procedere campionando la risposta della struttura da 1 Hz a 1200 Hz con 1200 campionamenti più 1, cioè procedendo a passo 1 Hz su quel range, perciò imposto le proprietà come in figura.

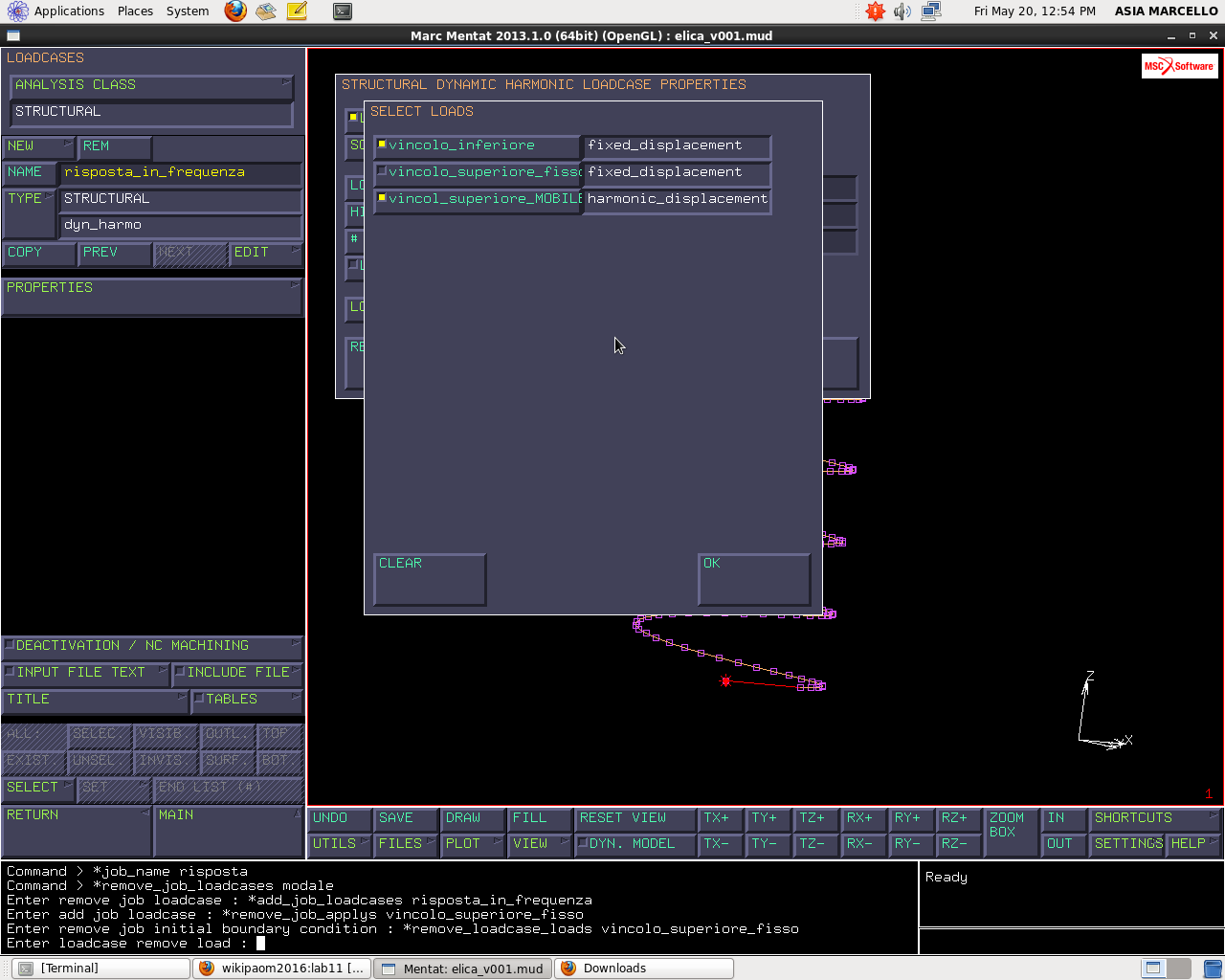
Creo un nuovo JOB copiando il job di estrazione modi propri e chiamando il nuovo “risposta”. Tra le proprietà attivo il loadcase “risposta_in_frequenza” e disattivo “modale”. Tra gli INITIAL LOADS disattivo il “vincolo_superiore_fisso”.

Inoltre, torno nel menu LOADCASES>PROPERTIES>LOADS e disattivo anche qui il “vincolo_superiore_fisso” lasciando gli altri due selezionati.

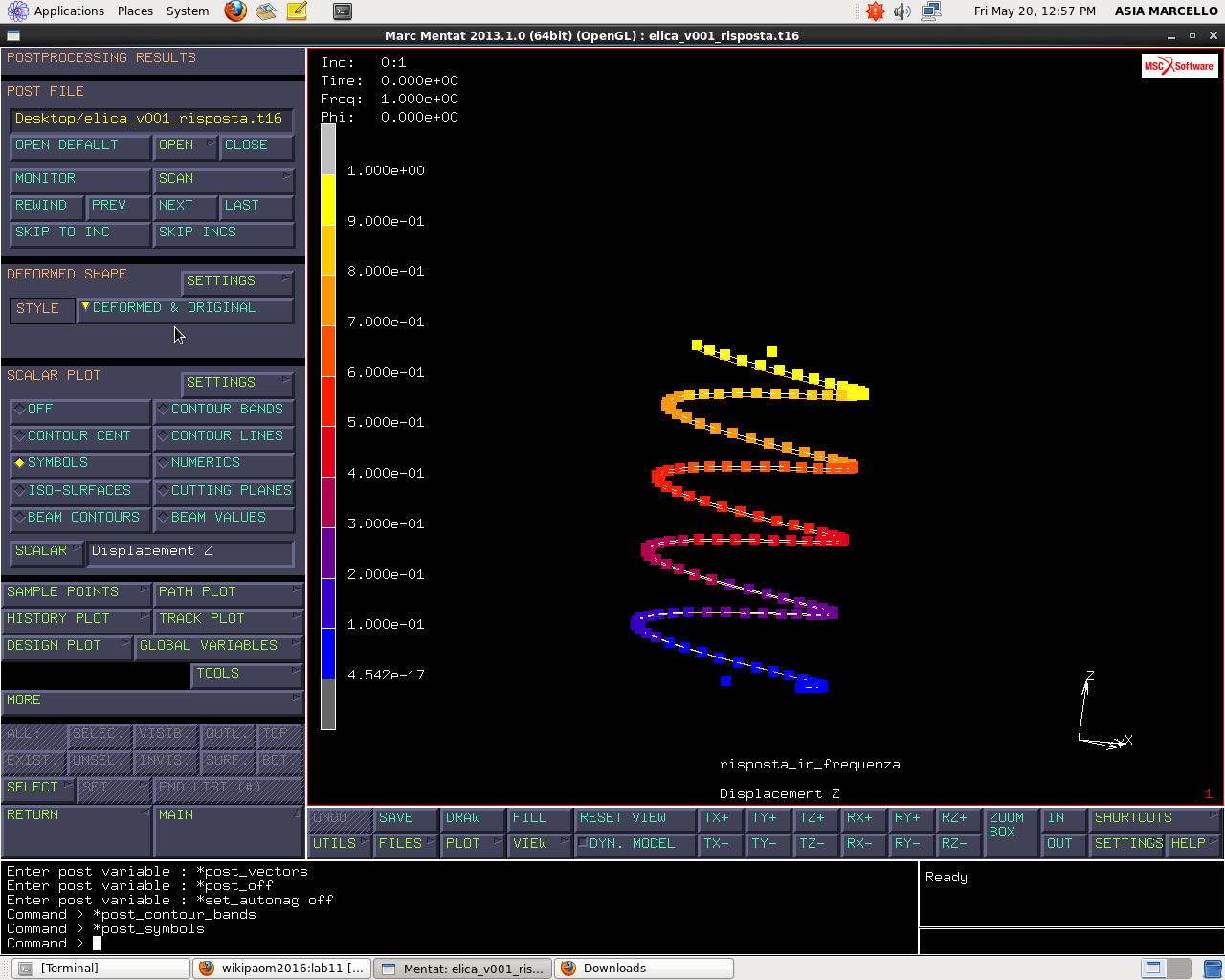
Torno in JOBS e lancio il calcolo con RUN>SUBMIT. In questo modo calcola la risposta in frequenza sulle 1200 frequenze di campionamento. Conviene fare questa analisi con una mesh molto snella. Apro il file dei risultati e trovo lo step 0 scarico, mentre già allo step 1 osservo che il nodo si è spostato di 1mm.

Aumentando la frequenza si osserva che gli spostamenti crescono. Arrivati a 580 Hz il sistema oscilla tra due configurazioni ed è ben visibile l’autocontatto tra le spire, pertanto in questa configurazione non si potrebbe lavorare.

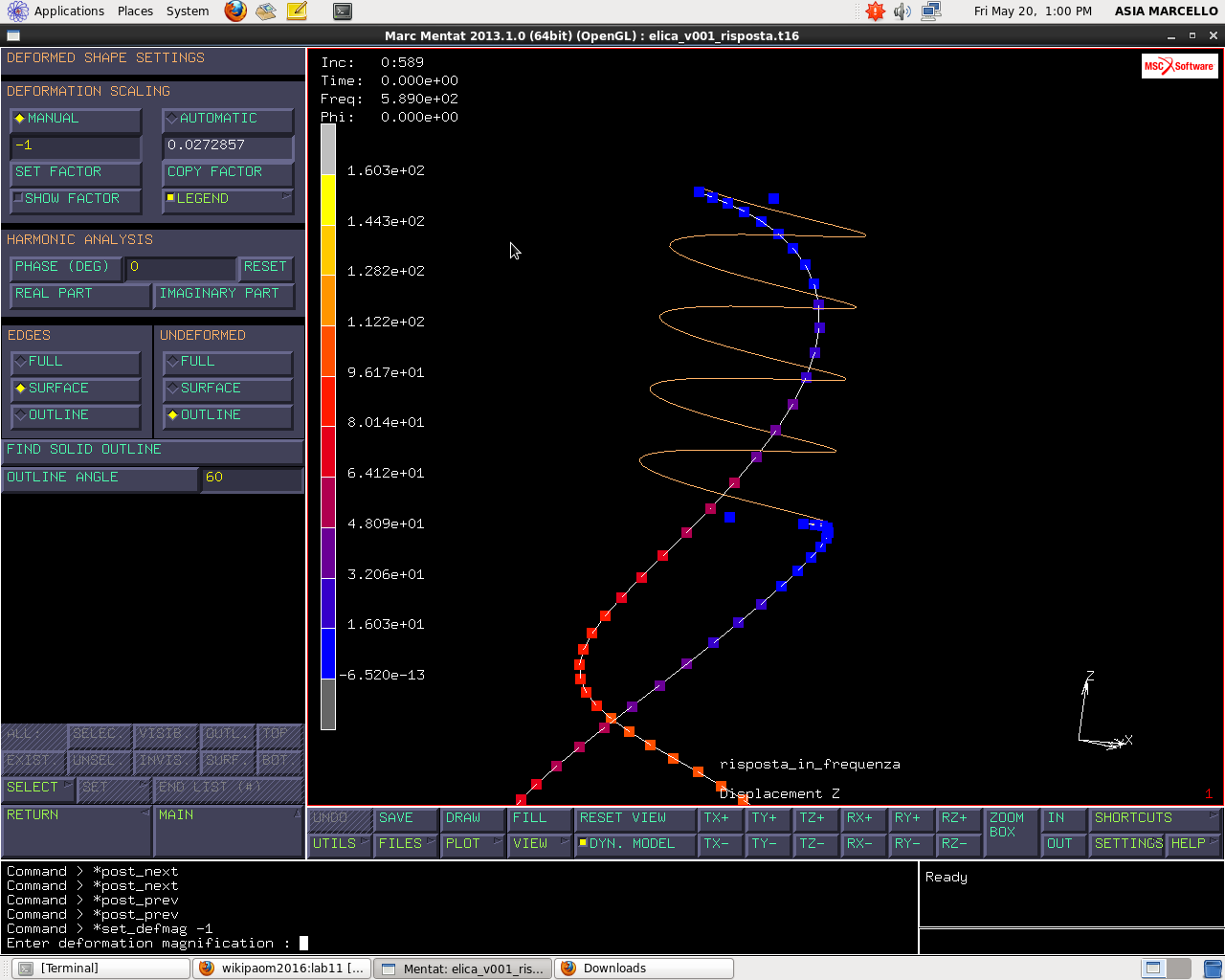
Procedo fino a 589 Hz e ottengo la deformata in figura. Osservazione: prima della risonanza il sistema oscilla in fase con le sollecitazioni, poi, superata la risonanza, oscilla in controfase. Proseguendo si normalizzano le sollecitazioni perché mi allontano dalla condizione di risonanza.

Formula per rilevare il punto stazionario (massimo o minimo) di una funziona parabolica campionata in 3 punti equispaziati, con valori di campionamento $y_1,y_2,y_3$. $$ y_{max}= \frac{+ 16 y_2^{2}+ y_1^{2} +y_3^{2} - 8 y_1 y_2 - 8 y_2 y_3 - 2 y_1 y_3 } {16y_2 - 8\left( y_1 + y_3 \right)} $$

elica_v000.mud elica_v001.mud

modello a fine lezione con risposta in freq. 0-1200 Hz SENZA SMORZAMENTO. La risposta risulta NON limitata in corrispondenza dei modi propri risonanti eccitati dalla forzante.

Per inserire uno smorzamento strutturale (es. 1% del critico) occorre seguire i seguenti step:

• entro nel menu menu MAIN → MATERIAL PROPERTIES → MATERIAL PROPERTIES;
• definisco preventivamente una table da menu TABLES, NEW → 1 INDIPENDENT VARIABLE
  • definisco NAME come modula_stiffmatmult
  • setto il TYPE della Indipendent variable v1 a frequency
  • definisco la table per FORMULA e batto 1/pi/v1, ossia definisco una $g(f)=\frac{1}{\pi f}$
• torno nel menu menu MAIN → MATERIAL PROPERTIES → MATERIAL PROPERTIES con RETURN;
• seleziono qui il materiale “titanio”, quindi entro nel menu STRUCTURAL → DAMPING e attivo DAMPING;
• lascio a valore nullo lo MASS MATRIX MULTIPLIER
• definisco uno STIFFNESS MATRIX MULTIPLIER pari allo smorzamento frazione del critico desiderato, nel caso specifico 0.01,
• lo modulo per una TABLE cliccando sul menu TABLE che affianca stiffness matrix multiplier
• scelgo la table modula_stiffmatmult appena definita, quindi do OK e ancora OK per tornare al menu material properties
• in questo modo ho definito lo smorzamento fraz. del critico in funzione dei coefficienti $\alpha$ e $\beta$ del Rayleigh damping, supponendo nullo $\alpha$ e quindi il contributo della matrice massa alla matrice smorzamento. In pratica ho $\zeta = \frac{1}{2}(\frac{\alpha}{2 \pi f}+2 \pi f \beta)$ con $\alpha=0$ e $\beta= 0.01 \cdot g(f)=\frac{0.01}{\pi f}$, da cui $\zeta=0.01$ come desiderato.
• passo quindi al menu MAIN → JOBS e creo una copia del job di risposta in frequenza non smorzata risposta selezionandolo e utilizzando il comando COPY in alto a sx
• rinomino in rispostasmorzata il nuovo job
• entro nel menu PROPERTIES, da cui seleziono ANALYSIS OPTIONS; qui attivo COMPLEX DAMPING dal blocco dynamic harmonic, quindi esco con OK
• vado quindi in JOB RESULTS e disattivo Stress e Equivalent von Mises stress
• inserisco al loro posto da AVAILABLE ELEMENT SCALARS
  • Equivalent Real Harmonic Stress , layers MAX & MIN
  • Equivalent Imag Harmonic Stress , layers MAX & MIN
  • le REAL HARMONIC e IMAG HARMONIC equivalenti delle componenti di sollecitazione dell'elemento trave come da paragrafo successivo, , layers DEFAULT, oltre al comune Beam Orientatio Vector
• inserisco da AVAILABLE ELEMENT TENSORS
  • Real Harmonic Stress , layers ALL
  • Imag Harmonic Stress , layers ALL
• Si procede quindi a lanciare il calcolo come di consueto da RUN → SUBMIT e aprendo il file dei risultati con OPEN POST FILE (RESULTS MENU)
• La deformata appare ora visualizzabile con fase entro il ciclo di oscillazione (vedere menu DEFORMED SHAPE SETTINGS); nel caso senza smorzamento la fase poteva essere solo 0° o 180°, casistica rappresentabile mediante una variazione di segno delle componenti di spostamento o di tensione monitorate. Ricordo che la componente reale ha fase 0° (modulata in $\cos(\omega t)$) mentre la componente immaginaria ha fase 270° (modulata in $\sin(\omega t)$). Ricordo inoltre che alla risonanza si amplifica fortemente la componente immaginaria della risposta, mentre si annulla quella reale (la risposta è infatti sfasata di ~90° rispetto all'eccitante).
• Raccogliamo a titolo di esempio lo spostamento in direzione $z$ del nodo 146 alla sezione centrale della molla:
  • dal menu POSTPROCESSING RESULTS, con file dei risultati t16 aperto, procedere entro il menu HISTORY PLOT
  • definire il punti di campionamento con SET LOCATIONS, fornendo quindi al prompt 146 [invio], seguito da un END LIST
  • definire il range di sottoincrementi di campionamento da INC RANGE, fornendo quindi al prompt 0:1 [invio], 0:1200 [invio], 1 [invio], come sottoincrementi di inizio, fine e passo di campionamento.
  • procedere a compilare diagrammi sulla base dei dati appena campionati dal menu ADD CURVES, quindi ALL LOCATIONS (ho selezionato un solo punto di campionamento); richiedo la compilazione di un grafico che abbia come asse delle ascisse la global variabl Frequency, e come asse delle ordinate Displacement Z Magnitude. Con FIT adatto le scale del grafico alla curva.
  • Con RETURN torno al menu HISTORY PLOT, ove posso ridurre la frequenza delle etichette indicanti l'incremento portando SHOW IDS da '1' a '100'.
• I picchi di risposta alle risonanze appaiono ora finiti (non erano limitati in assenza di smorzamento), con oscillazione massima dell'ordine dei 30 mm in corrispondenza della prima pulsazione propria. È ora visibile che alcuni modi propri, pur non essendo strettamente ortogonali all'eccitante, risultano scarsamente accoppiati e facilmente contenuti da un ridotto smorzamento strutturale.

Grafico di risposta del sistema smorzato in termini di ampiezza di oscillazione z di un nodo a centro molla in funzione della frequenza del moto eccitante. Occorre verificare le ampiezze di oscillazione tra due sezioni corrispondenti di spire contigue per verificare che non vi sia compenetrazione tra le spire.

Nel grafico sono riportate le risposte in termini di ampiezza di oscillazione z di un nodo a centro molla in funzione della frequenza del moto eccitante per il caso NON smorzato (curva rossa) e per il caso smorzato (curva verde) con smorzamento 1% del critico. Si nota che nel caso smorzato alcuni picchi di risposta risonante sono ridotti in entità fino ad essere coperti dalle code del modo principale. Si consiglia quindi di inserire un pur piccolo smorzamento (es. 0.001 del critico) per filtrare i modi risonanti eccitati solo in misura minimale.

è possibile ottenere i consueti diagrammi di sollecitazione inserendo da JOB RESULTS gli available element scalars

• Beam orientation vector
• Beam axial force
• Beam bending moment local X
• Beam bending moment local Y
• Beam shear force local X
• Beam shear force local Y
• Beam torsional moment

Queste caratteristiche di sollecitazione sono quindi visualizzabili dalla seconda parte del menu POSTPROCESSING RESULTS, quella accessibile via MORE, attraverso il blocco menu BEAM DIAGRAM. Alcune sollecitazioni (es. il taglio negli elementi trave alla Eulero-Bernoulli) potrebbero essere non definite.