Indice
Energia potenziale elastica della trave curva piana
Formula per l'energia interna di una trave curva nel piano. Lo sforzo normale $N$ è supposto positivo se trattivo, il momento flettente $M_f$ è supposto positivo se tende le fibre all'intradosso (ossia se tende a raddrizzare la trave); nel caso questa seconda convenzione non sia rispettata occorre variare il segno del termine misto $M_f N$.
$$ \def\d{\,\mathrm{d}} U= \int_{0}^{\Phi} \left( \frac{M_{f}^2 }{2 E A \delta r_g} + \frac{N ^2}{2 E A} +\xi \frac{T ^2}{2 G A} - \frac{N M_{f}} { E A r_g} \right) r_g \d \phi $$
ove $A$ è l'area di sezione, $r_g$ è il raggio baricentrico (supposto costante), $\delta=r_g-r_n$ è la distanza tra questi è il raggio neutro, e, per sezioni circolari piene, $\xi= 1.11$, e
$$ r_n = \frac{\left(r_e-r_i\right)^2}{8\left( \frac{r_i+r_e}{2} - \sqrt{r_i r_e} \right)} $$
ove $r_i,r_e$ corrispondono ai raggi interno ed esterno.
La tensione assiale indotta dal momento flettente è ricavabile come
$$ \sigma_f = \frac{M_f \left(r_n - r\right)}{A \delta r} $$
Continuazione MAGLIA DI CATENA
maglia di catena, modello cattedra fine lezione ven 4 mar, formato wxm
Definiamo assi locali (η, ε e ζ) nella sezione della maglia di catena considerata come trave:
- ζ - allineato con l'asse baricentrico della trave;
- η e ε - ortogonali all'asse baricentrico della trave. Nella Figure 1 l'orientamento di ε è stato definito ortogonale al piano XY e quello di η è ottenuto di conseguenza per la regola della mano destra.

Per le sezioni circolari non è necessario indicare come sono orientati nello spazio η e ε sezione per sezione, perché la sezione ruotata rimane uguale a se stessa. Tuttavia se la sezione della trave è ellittica può essere necessario indicare in quale direzione si trova il semiasse maggiore, visto che la risposta della maglia di catena cambia a seconda di dove si trova il semiasse maggiore.
La struttura della maglia di catena possiede due piani di simmetria e di conseguenza se riesco a risolvere il problema elastico su 1/4 di struttura è possibile ricavare il comportamento degli altri 3/4 semplicemente per reazioni di simmetria. Aggiungendo i vincoli ottenuti dalla continuità del materiale e dall'analisi delle condizioni di simmetria la struttura da analizzare diventa:

La struttura ottenuta è una volta iperstatica, la semplifichiamo sostituendo il doppio pendolo superiore con un carrello e aggiungendo la coppia C relativa al vincolo soppresso, in modo che sia risolvibile il problema strutturale.

Dall'equilibrio della struttura abbiamo trovato FA = 0.
Nella lezione precedente la struttura è stata risolta supponendo che l'energia potenziale elastica U sia prodotta esclusivamente dal momento flettente - Ipotesi di trave dritta snella. $$ \def\d{\,\mathrm{d}} U= \int_{l} \frac{M_{f,\xi}^2}{2 E J_{\xi \xi }} \d l $$ In realtà il momento flettente è solo una delle possibili sollecitazioni che agiscono sulla trave, poiché trattando un sistema piano avremo anche lo sforzo di taglio T e lo sforzo normale N - Ipotesi di trave dritta, con l'aggiunta di T e N la formula dell'energia potenziale elastica U diventa:
$$ \def\d{\,\mathrm{d}} U= \int_{l} \frac{M_{f,\xi}^2}{2 E J_{\xi \xi }} + \frac{N ^2}{2 E A} +\eta_{\xi}\frac{T_{ \xi}^2}{2 G A} \d l $$
Si ricava il taglio e lo sforzo normale su ogni tratto della struttura:

$$N1(\theta )=FAcos(\theta )+\frac{P}{2}sin(\theta )$$ $$T1(\theta )=\frac{P}{2}cos(\theta )-FAsin(\theta )$$

$$N2=\frac{P}{2}$$ $$T2=FA$$
Verifica trave snella e curva
Abbiamo utilizzato dei dati presi a campione da un catalogo di produttori di catene industriali:
- d filo = 10 mm;
- Raggio interno Ri = 6.5 mm (R = 11.5 mm);
- passo = 30 mm (passo-2*Ri = 2L = 17 mm).
La trave in questione presenta un rapporto lunghezza/diametro piccolo (vicino a 3), quindi non può essere considerata snella. A tal proposito risulta indispensabile introdurre nella trattativa sforzo di taglio e sforzo normale.
Si osserva inoltre che il raggio di curvatura dell'asse baricentrico (R) non è molto maggiore dello spessore radiale della sezione, e ciò rende la curvatura non trascurabile. Si deve necessariamente studiare il problema anche attraverso la teoria della trave curva.
Dalle verifiche precedenti risulta necessario considerare il problema anche attraverso la teoria della trave curva, con la quale si calcola l'energia potenziale elastica U dell'arco di circonferenza (tratto 1 - vedi Figure 3) attraverso: $$ \def\d{\,\mathrm{d}} U= \int_{0}^{\Phi} \left( \frac{M_{f}^2 }{2 E A \delta r_g} + \frac{N ^2}{2 E A} +\xi \frac{T ^2}{2 G A} - \frac{N M_{f}} { E A r_g} \right) r_g \d \phi $$
Nel foglio di calcolo presente all'inizio di questo paragrafo sono presenti entrambe le soluzioni:
- Teoria della trave dritta con T e N;
- Teoria della trave curva.
A seguito sono riportati i passaggi per giungere al calcolo dell'energia potenziale elastica U attraverso le due strategie elencate:


A conclusione dei calcoli si esegue il confronto relativo ai metodi attraverso il rapporto tra l'allungamento della maglia di catena e allungamento del tondino relativo, con lunghezza definita dal passo della maglia, composto dello stesso materiale e con pari sezione:
- Trave dritta snella - maglia di catena (trascurando N e T) 1.75 volte più cedevole del tondino d'acciaio;
- Trave dritta considerando T e N - maglia di catena 3.2 volte più cedevole del tondino d'acciaio;
- Teoria Trave curva - maglia di catena 3.14 volte più cedevole del tondino d'acciaio.
Da questa verifica possiamo osservare che non c'è molta differenza nella risposta ai carichi nel considerare il tratto 1 della maglia di catena come trave curva e trave dritta (con T e N). Invece se consideriamo la maglia di catena come una trave dritta snella si commette un errore dell'ordine di circa 50%.
Si può ricavare il momento flettente nella struttura, coincidente con la coppia C, già definita, e conseguentemente valutare lo stato tensionale al punto di applicazione della coppia stessa: [attenzione che il raggio r non è quello baricentrico, ma è quello a cui si campiona la tensione, ossia (r-d/2)]
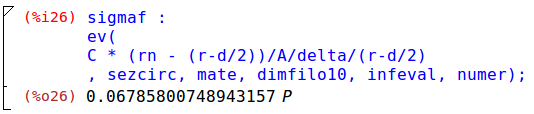
Quanto visto, varia in funzione della sezione che si caratterizza, delle sue proprietà strutturali e geometriche. [Sezione circolare a dimensioni e materiale definiti] Per maggiore accuratezza si può verificare il carico garantito con i manuali utilizzati per le dimensioni della catena. 1)
Comandi MAXIMA
Di seguito sono presenti una serie di funzioni utili alla risoluzione di alcune problematiche con l'ausilio del calcolatore.
Definizione di Funzioni
Definire una funzione può avvenire attraverso due diverse strategie:
La prima prevede l'assegnazione della funzione con “:” :

Questo comando implementa le funzioni valutandole all’atto della definizione e non all’atto della chiamata. Utilizzando la funzione “ev”, in figura, posso assegnare alla variabile x un qualsiasi valore specifico, al fine di sostituirla all'espressione e determinarne il valore. Nel caso in cui risulti utile ripetere l'ultimo passaggio per differenti valori della variabile di funzione, si può pensare di utilizzare un metodo più compatto e sintatticamente più utile.
Il secondo invece definisce la funzione con il comando“:=” :

Tale tipo di sintassi non prevede la valutazione, al momento dell'assegnazione, dell'espressione che è a destra di “:=” .
Se non voglio ritardare la valutazione della funzione utilizzo il comando “define” :

Naturalmente si posso definire funzioni in più variabili:
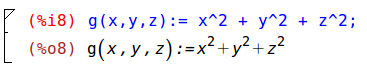
Grafici e Sviluppo in Serie di Taylor
Sviluppo in serie di taylor la funzione precedentemente vista:

Nel comando troviamo la funzione, la relativa variabile, seguita da intorno e grado di sviluppo; in questo caso “fun(x)” nella variabile x, nell'intorno specifico di $\pi/6$ al primo ordine.2)
Assegno a “t1fun” e “t2fun” gli sviluppi in serie di Taylor rispettivamente al primo e al secondo ordine


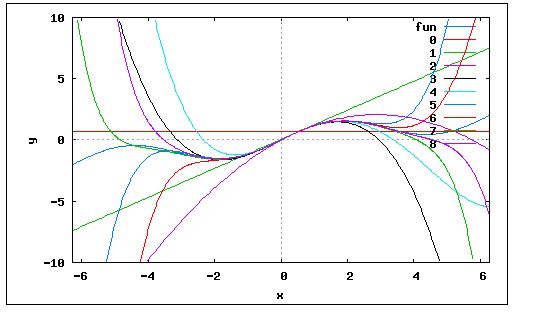
Si possono graficare le funzioni attraverso due metodi:un metodo standard con comando “wxplot2d” che genera il grafico nella pagina di lavoro: qui il primo parametro può essere o una singola funzione,o una lista di funzioni, il secondo parametro è una lista che contiene la variabile da far scorrere e gli estremi dell'intervallo in cui essa varia. Con il terzo parametro, invece facoltativo, si può indicare una legenda sul grafico, qualora quella di default non soddisfacesse le richieste dell'operatore.

Un secondo metodo prevede la stesura del grafico in una finestra flottante diversa dal foglio di lavoro, scrivendo “plot2d”.
Si può automatizzare la procedura, calcolando lo sviluppo in serie di Taylor a gradi superiori, per poi graficarli. Un blocco di istruzioni è un insieme di comandi dati al calcolatore, limitati da parentesi tonde, con output dato dall'ultima espressione.

“plottami” è definita come una lista quota.

Allora si può passare all'estrazione della serie di Taylor imponendo l'ordine pari ad “i=3”.
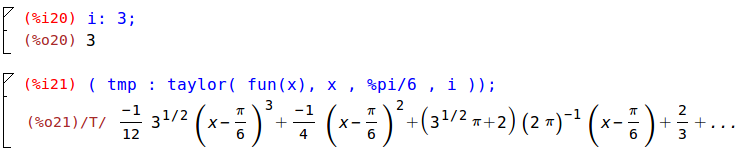

Attraverso l'ausilio di “append”, con cui accodiamo una funzione ad un'altra, si può aggiungere alla definizione di “plottami”, la lista “legendami”, definita come concatenazione di se stessa con l'elemento che contiene per esempio i. Nel “plottami” si ha come primo parametro la lista di funzioni di riferimento, come secondo, la variabile seguita dal range di “plotaggio”, seguita ulteriormente dalla lista “legendami” ed infine da una seconda variabile e il relativo intervallo.
NOTE
Autori
Federico Rizzello, mat. 106165, Riccardo Tramacere, mat. 104297, Rafael Caberlon, mat. 103519.
Tabella di monitoraggio carico orario
PATTUME
Lista dei simboli
| $u$,$v$,$w$ | spostamenti in direzione x,y,z rispettivamente |
| $\alpha$ | fattore di scala dell'elemento triangolare, vedi Figura 19 |

Discussione
Note di prima revisione
REVISORE 1
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
Ho trovato solo errori di tipo ortografico/grammatico:
REVISORE 2
ho letto il lavoro fatto dai colleghi e secondo me il lavoro è stato fatto bene, perciò non ho visto molto da correggere a parte qualche errore di grammatica che riporto qua:
1-Dalla verifiche precedenti risulta necessario considerare il problema anche attraverso la teoria della trave curva, con la quale si calcola l'energia potenziale elastica U dell'arco di circonferenza (tratto 1 - vedi *Figure 3*) attraverso:
2-Naturalmente si posso definire funzioni in più variabili: <https://cdm.ing.unimo.it/dokuwiki/_detail/wikipaom2016/funzione_4_lez5_.png?id=wikipaom2016%3Alab2> Cordiali saluti.