cdm.ing.unimore.it

Nell’ultima lezione abbiamo realizzato la modellazione di un tubo internamente pressurizzato: dopo aver realizzato la meshatura e aver imposto le proprietà costitutive del materiale, abbiamo inserito i vincoli di posizionamento che ci garantiscono soluzione univoca in termini di spostamenti, rendendo la matrice della struttura non singolare. Non resta che avviare la procedura di calcolo:

Creiamo un JOBS (lavoro di calcolo) senza avere il vincolo di impostare la storia di carico del nostro tubo MAIN > LOADCASES, perché da $t=0$ abbiamo direttamente una $P_{int}= 10 Mpa$ che si mantiene costante nel nostro problema.

Trovandoci in un caso di lineare, possiamo semplificare la trattazione considerando una pressione di $1 MPa$ per poi moltiplicare per $10$ i risultati ottenuti. Creiamo un JOBS rinominandolo $pint$ di tipo STRUCTURAL , inoltre dal menù PROPERTIES possiamo attivare/disattivare LINEAR ELASTIC ANALYSIS, ma è pressoché ininfluente, al massimo andremmo ad ottimizzare lo stato della memoria. Poi sempre dal menù PROPERTIES operiamo su INITIAL LOADS che riporta un listato delle BOUNDARY CONDITIONS precedentemente definite: nel nostro caso saranno tutte attive nell’effettuare il calcolo. Su JOB RESULTS scegliamo i risultati da visualizzare al termine del calcolo, in questo menù possiamo individuare due diverse aree:

1. 1 un’area relativa alle caratteristiche tensionali e de formative dell’elemento. Gli output (risultati) di nostro interesse sono:

• “TOTAL STRAIN”: che racchiude la totalità delle deformazioni
• “STRESS”
• “EQUIVALENT VON MISES STRESS”

Tuttavia vi sono come ulteriori possibilità:

• “ELASTIC STRAIN”: somma delle deformazioni elastiche
• “THERMAL STRAIN”: per deformazioni termiche
• “LOG STRAIN”: utilizzato quando le deformazioni sono di entità elevata
• Etc…..

1. 2 un’area relativa al nodo i cui output di interesse sono:

• “DISPLACEMENT”
• “EXTERNAL FORCE”
• “REACTION FORCE”
• “TYNING FORCE” sono le forze applicate dai vincoli cinematici alla struttura qualora esistano (potremmo anche avere i TYINIG MOMENT che sarebbero i corrispettivi duali in termini di momenti, ma che per la struttura in oggetto non sono considerati).

Sono quantità calcolate nei punti di integrazione dell’elemento ALL POINTS (all integration points) riferiti ai punti di Gauss.

Mentre nell’area nodale vi è la possibilità di mantenere la modalità default che ci da in output quantità predefinite, oppure possiamo usare il comando CUSTOM, che ci permette di scegliere arbitrariamente le quantità da calcolare. - Cosicché ho definito i risultati che voglio convertire in forze nodali. Dal menù JOBS > PROPERTIES è possibile agire anche sulle voci:

• ANALYSIS OPTIONS attiva alcune varianti del calcolo, ma in questo caso lineare non servono perché sono trascurabili (nel caso lineare queste varianti sono piccole)
• ADVANCED OPTIONS è da attivare nel caso di non linearità del calcolo
• JOB PARAMETRES è il comando che ci permette di selezionare il solutore che utilizzeremo per il calcolo: per problemi simmetrici (se non è simmetrico studio la parte simmetrica di esso) esso potrà essere lineare (MATRIX SOLVER), scegliendo nel sottomenù MATRIX SOLVER, il metodo di calcolo diretto MULTI FRONTALS SPARSE; quest’ultima tipologia di calcola può essere preferita ai metodi di calcolo iterativi, che benché allochino poca memoria possono non convergere.

In JOB PARAMETRES troviamo SHELL/BEAM LAYER che definisce la discretizzazione lungo lo spessore. Inoltre i nostri calcoli vengono eseguiti in EXTENDED PRECISION (doppia precisione).

Definito il modello vado in JOBS>CHECK, che può darmi informazioni sugli errori che ho commesso oppure può darmi avvertimenti (WARNINGS) che non inficiano la correttezza del calcolo ma potrebbero in futuro diventare errori (il programma mi mette in guardia). Come risultato del CHECK abbiamo che sono stati rilevati 1920 elementi di tipo 7 tali per cui non erano state definite le proprietà del materiale, perciò automaticamente Marc associa a tali 1920 elementi l’elemento hex 8; volendo potremmo effettuare tale assegnazione manualmente attraverso il menù ELEMENTS TYPE > SOLID in tale schermata sono presenti le tipologie degli elementi classificati in base al numero di nodi e al tipo di integrazione assegnabili alle 1920 celle non definite della nostra mesh.

FULL INTEGRATION: definisce i punti di integrazione ai fini del calcolo della matrice rigidezza: nel nostro caso si usa tale tipo di integrazione che si basa su due punti di integrazione su ogni asse, quindi 8 punti di integrazione totale. FULL & HERRMANN FORMULATION se stiamo lavorando con dei materiali incomprimibili (che è l’elemento 84); REDUCED INTEGRATION se vogliamo lavorare con un solo punto di integrazione al centroide invece che 8 (elemento 117); scegliamo l’elemento 7 che è quello che ha effettivamente scelto Marc di default e l’associamo a tutti gli elementi con ALL EXIST.

JOBS > RENUMBER ALL: consente di colmare dei buchi nella numerazione dei nodi (es. se tra 1 2 e 3 cancello 2 per qualsiasi motivo il punto 3 verrà rinominato 2) quindi inutile se vogliamo affidarci ancora alla numerazione iniziale

RUN: è il menù da dove potremmo lanciare il calcolo: la partenza effettiva del calcolo è determinata dal comando SUBMIT, il calcolo è semplice ma prima di effettuarlo il programma estrae dal modello un file di input (.mud). Quindi viene lanciato il solutore con SUBMIT a seconda dell’$EXIT NUMBER$ possiamo stabilire se è andato a buon fine o se contiene errori. Il numero che ci assicura la riuscita del calcolo è “$3004$” però a volte potremmo commettere degli errori legati alla eccessiva singolarità della matrice: questi errori vengono regolati da un parametro che prende il nome di SINGOLAR RATIO. Se esso è troppo elevato la matrice sarà troppo singolare e mal condizionata, questo errore è rappresentato dal numero “$2004$”. ANALYSIS TIME: indica il tempo in cui il calcolo opera con determinate BOUNDARY CONDITIONS (solitamente esse variano nel tempo sollecitando il modello in maniera diversa)

Nella cartella di origine del file, una volta avviato il SUBMIT genereremo 4 nuovi file che possiamo ricercare in APPLICATIONS → SYSTEM TOOL → FILE BROWSER .dat : file prettamente di calcolo anche leggibile con un programma di testo

• $.log$: diario scarno di calcolo e della memoria allocata
• $.t16$: contiene i risultati che abbiamo richiesto in JOB RESULT ed è un file binario
• $.out$: diario dettagliato di calcolo, al suo interno troviamo gli errori nel calcolo ( un errore comune può essere non impostare modulo di Young→ EXIT NUMBER=13). Quindi da .out→SERCH FIND ERROR e lo trovo immediatamente.

Per aprire il $.t16$ usiamo il comando OPEN POST FILE (RESULT MENU’), oppure se invece da MAIN MENU→POST PROCESSING→RESULTS→OPEN DEFAULT ottengo l’ultimo calcolato( con OPEN ne apro uno a mio piacimento). Quando sulla schermata in alto appaiono $INCREMENTO$ e $TEMPO$ ci troviamo nel file dei risultati in cui non ha senso apporre modifiche perché non sarebbero salvabili quindi dobbiamo uscirne con CLOSE e andare sul file proprio del modello per apporre modifiche nel caso ce ne sia il bisogno. PREVIOUS e NEXT servono per procedere indietro e avanti nel tempo di simulazione.

DEFORMED SHAPES: la struttura può inoltre essere visualizzata nella forma deformata (DEFORMED) di Default ma non sempre il fattore di scala ci permette di visualizzare correttamente la deformazione; attraverso SETTING→DEFORMATIONS SCALING possiamo scegliere un fattore di scala arbitrario (MANUAL) oppure lasciar fare a Marc AUTOMATIC. Inoltre si può scegliere di visualizzare il fattore di scala attivando il led alla voce SHOW FACTOR. La struttura può essere inoltre visualizzata nella sua forma indeformata (ORIGINAL) o in una terza forma in cui la deformata e l’indeformata sono sovrapposte e confrontabili (DEFORMED AND ORIGINAL) Infine facciamo delle precisazioni su 2 comandi: “EQUIVALENT VON MISES STRESS”: è uno scalare e lo plotto con menu SCALAR PLOT (quindi SC. PLOT→EQUI. VON MISES STRESS) “CONTOUR BANDS”: colora le bande a seconda dei valori associati ai nodi riguardo della tensione di Von Mises

Prima di considerare l’altra parte del menù [EXTRAPOLATION] è utile andare a studiare come vengono determinate le grandezze richieste nel comando JOB da parte del risolutore $(MARC)$. In particolare attraverso i punti di integrazione di Gaus possiamo calcolare l’integrale esatto di una generica funzione con dominio l'elemento considerato, semplicemente dalla sommatoria dei valori pesati di tale funzione calcolata nei soli punti di Gauss. Il nostro problema è determinare i valori della tensione ai nodi Innanzitutto definiamo un centroide su ogni elemento e assegniamo a questo un valore tensionale pari alla media della sigma sui 4 punti di integrazione. Ci sono diverse procedure per indivudare tali tensioni sui nodi; queste si possono scegliere da: POST PROCESSING > RESULTS > SCALAR PLOT – SETTING > EXTRAPOLATION

• Selezionando METHOD-LINEAR il valore della tensione nel nodo corrisponde a quella che si avrebbe procedendo linearmente tra il valore della tensione del centroide (dal metodo di Gauss ) e quello calcolato per il rispettivo punto di integrazione. Vediamo un esempio per capire:

il problema in questo caso sta nel fatto che un nodo potrebbe risultare con tensione superiore a quella di snervamento del materiale, poiché è limitata solamente nel calcolo, che avviene nei punti di integrazione. E' inoltre possibile che si abbia una tensione negativa in un nodo, che indicherebbe una contropulsione, che non rispecchia il caso reale. Si riportano degli esempi per esprimere queste considerazioni:

• Per risolvere il problema si può selezionare il metodo [TRANSLATE], che va a “traslare” il valore ottenuto sul punto di integrazione direttamente sul nodo, senza modificarlo. Risulta quindi in svantaggio di sicurezza rispetto al metodo lineare ma si utilizza per evitare gli errori sopra descritti.

• Il metodo [AVERAGE] invece, definisce in tutto l’elemento il valore della tensione propria del centroide, calcolata dal metodo di gauss, quindi dalla media dei valori nei punti di integrazione. È quindi il metodo più grossolano.

Tuttavia per il nodo centrale avrò quattro valori diversi, si possono associare i valori con due diverse procedure: Se “NODE AVERAGING” è ON prendo la media di questi 4 valori distinti e la assegno al nodo centrale. Se “NODE AVERAGING” è OFF mantengo per ogni nodo un valore distinto “base-elemento” invece di associare uno stato tensionale univoco definito dalla media come nel caso precedente. Quindi si associano agli elementi 4 stati tensionali, che si ripercuotono con colore diverso su ciascun elemento. Così facendo preservo la naturale discontinuità delle tensioni tra elemento ed elemento. Quando utilizziamo la “media nodale” è come se trascurassimo e nascondessimo questa discontinuità, tuttavia la raffinatezza della mesh è strettamente collegata alla discontinuità perché essa è appunto più accentuata nelle zone in cui la mesh è grezza.

Nel nostro caso particolare scegliamo una estrapolazione di tipo lineare con [NODAL AVERAGING] impostato su OFF. Dal percorso [RESULTS]>[SCALAR] scelgo la quantità di interesse [EQUIVALENT VON MISES STRESS]

In base a quello che voglio plottare scelgo il campo di specifico interesse:

• CONTOUR BANDS indica la transizione tra una banda e l’altra, caratterizzata da un colore diverso a seconda del valore della tensione di Von Mises :

si nota che l’andamento di tali bande appare omogeneo sia assialmente che circonferenzialmente;

• ISOSURFACES ci permette di conoscere ciò che accade all’interno del volume, plottando le superfici con un uniforme valore di Von Mises.

Esse sono utili per conoscere ciò che c’è all’interno del modello e contengono la direzione $“z”$ e ciò implica che in questa direzione lo stato tensionale è omogeneo. Se provo ad effettuare un’analisi attraverso altri tipi di tensioni mi accorgo che anch’esse su $“z”$ presentano un andamento omogeneo, dunque anche le componenti della tensione sono costanti in $“z”$. Una vista di superficie mi permette di conoscere come varia uno scalare anche nel volume, mentre le CONTOUR BANDS sono indicate per analizzare lo stato di transizione superficiale.

• CUTTING PLANES: definiscono sezioni della struttura e sulle sezioni stesse viene plottato il valore della tensione di riferimento. Vado dunque a SETTINGS → CUTTING PLANES: qui potrei affettare la nostra porzione di tubo utilizzando dei piani di taglio.

in particolare utilizzo $10$ piani di taglio spaziati di $2$ . Inoltre posso variare inclinazione dei piani facendo variare la normale. Per l’analisi del nostro modelle però è più adatto il CONTOUR BANDS.

Ho una simmetria cilindrica, quindi potrebbe tornare comodo studiare la struttura con coordinate polari, dunque per variare sistema di riferimento devo prendere le informazioni in coordinate $x,y,z$ globali dal file dei risultati e operare un cambio di coordinate. Modifico dunque il tensore degli sforzi e le composizioni di vettori. Vado su SCALAR PLOT SETTINGS →RESULTS COORDINATES SYSTEM (di default non attivo)→ACTIVE. Così facendo ottengo un cambio di sistema modificando la terna delle coordinate: posso cambiare l’origine. A questo punto attivo il sistema di coordinate cilindriche(SYST CIL) che di default presenta un asse parallelo all’asse $“z”$ ed è passante per l’origine degli assi: ci va bene questo per il modello attuale. Gli assi di questo sistema sono differenti da $x,y,z$, il primo è l’asse Radiale, il secondo circonferenziale e il terzo appunto in direzione assiale. Nel nostro caso la tensione radiale $(component 1.1 of stress)$ secondo la soluzione esatta dovrebbe valere $-10 MPa$ sul bordo interno e $0 MPa$ su quello esterno ma in realtà misurano $-9.39$ e $-0.05 MPa$. Questa discrepanza è dovuta alla poca raffinatezza e alla scarsa esattezza delle $Boundary Conditions$ assegnate alle tensioni nodali, a differenza di quelle vincolari che invece rispecchiano al massimo l’esattezza della soluzione.

La sigma di Von Mises però è indipendente dal sistema di riferimento e soprattutto non tiene conto della quota idrostatica della pressione. La $component 2.2 of stress$ quindi è la tensione tangenziale, e all’interno misura $17.6 MPa$ e all’esterno $6 MPa$ (questi sono valori leggermente approssimati).

La $component 3.3 of stress$ cioè quella che si riferisce all’asse $z$ oscilla tra $-1.18$ e $1.18 Mpa$, ma secondo la soluzione esatta dovrebbe essere nulla, in quanto riconducibile ad un problema di tensione piana. Tuttavia se la mesh non è raffinata e se applichiamo dei metodi matematici, per questo tipo di analisi ci sarà sempre un residuo non nullo. La $\sigma _{z}$ deve essere ridotta il più possibile, poiché sono presenti variazioni di tensione tra elemento ed elemento a causa del tipo di discretizzazione.

Effettuando però la media tra il valore negativo e positivo risultato è nullo, ciò avviene simmetricamente in tutto il volume, escludendo i bordi. Notiamo che l’andamento della tensione in direzione radiale è a dente di sega, e si infittisce più al bordo interno che in quello esterno. Ogni quantità tensionale ha discontinuità massima al bordo interno.

Nelle zone con alto gradiente, la $\sigma _{z}$ ha oscillazioni maggiori, ovvero la soluzione si discosta da quella esatta. Dunque devo infittire la mesh nelle zone ad alto gradiente (per esempio in direzione circonferenziale il gradiente è nullo), quindi è indicato farlo lungo la direzione radiale. Mai infittire in senso assiale. Lo $shear locking$ è un fenomeno dovuto a coppie flettenti che si generano in corrispondenza delle zone in cui la tensione è discontinua, esso non permette inoltre il cambiamento di curvatura utile per la variazione del raggio interno da $r$ a $r+dr$. E’ per questo che dopo aver infittito la mesh radialmente ci sarà bisogno di infittirla anche circonferenzialmente proprio per impedire lo shear locking. Quindi nella meshatura è sconsigliato utilizzare elementi “distorti” ovvero con preponderante sviluppo radiale mentre quello cinconferenziale praticamente nullo. Quindi abbiamo visto che la componente tensionale in z è non nulla ma il suo valore è di difficile interpretazione ingegneristica. Ora scegliamo “COMPONENT 3.3 OF TOTAL STRAIN” oppure “COMPONENT 3.3 OF ELASTIC STRAIN” questa è $\epsilon _{z}$. La deformazione sull’asse $z$ è dell’ordine $10e-6$ o $10e-7$ mentre quelle in direzione circonferenziale sono dell’ordine di $10e-4$, tuttavia non sono trascurabili. Ora analizziamo le reazioni vincolari dei vincoli di posizionamento, MORE>VECTOR PLOT>EXTERNAL FORCE

Così facendo visualizziamo i vettori rappresentanti le riduzioni ai nodi delle pressioni distribuite che abbiamo inserito sul modello. A questo punto attivo le forze nodali su ON e visualizzo sui nodi prevalentemente due aree. Il Giallo è indicatore di circa $39 N$ e il Rosso di circa $19.5 N$, la metà poiché spinge su una porzione ad area circa doppia rispetto a quella in giallo.

Le reazioni di posizionamento sono non nulle ma le frecce sono troppo sottili quindi andiamo in SETTINGS da VECTOR PLOT e modifichiamo il “Fattore di Scala” adimensionale.

Nei nodi non vincolati c’è disequilibrio nodale tra le forze esterne e le forze elastiche degli elementi concorrenti al nodo, tale disequilibrio viene visualizzato in forma di reazione vincolare. La pressione applicata è un carico autoequilibrato, presenta uno scompenso minimo nella distribuzione, tuttavia quel residuo non dovrebbe esistere. Nessun nodo ha reazioni nulle.

Un errore è quello di rendere iperstatico il modello, tramite i vincoli di posizionamento. Ad esempio, blocco 7 gradi di libertà. Errore comune è quello di imporre un vincolo di posizionamento ad una faccia intera.

Dopo aver modificato il fattore di scala delle frecce seleziono ARROW PLOT SETTING, plotto le frecce solide passando da WILDFRAME a SOLID. Se tra la mia reazione vincolare e le altre forze ai nodi non vincolati non c’è una differenza di ordine $10e7$ vado in BOUNDARY CONDITION, rimuovo 11 su 12 vertici e lascio quello con corretto posizionamento→ lancio il mio modello → da POST PROCESSING RESULTS vado a MORE→ TENSOR PLOT → andiamo a plottare il tensore degli sforzi.

Scegliamo gli stress→ ALL PRINCIPAL VALUE→RESET VIEW→FILL ottengo una vista dove per ogni elemento vengono plottate a centro elemento le componenti principali di tensione. Tali componenti sono calcolate come valor medio di quanto calcolato ai punti di Gauss.

Sono 3 contributi verso il centro (e quindi compressivi) ma quello di z è praticamente nullo. Le frecce in direzione radiale e circonferenziale sono rispettivamente entrante ed uscente dal centroide.

Per interpretare tale visualizzazione immagino un cubetto elementare con le facce normali alle 3 direzioni principali soggetto a queste 3 tensioni dirette tipo $\sigma$.

Le frecce sono colorate in base alla scala graduata a lato modello; in particolare il blu è associato ai valori più compressivi e il giallo ai più trattivi sul modello.

La freccia blu è la compontente tensione radiale (perché così orientata), la più negativa di esse, la sigma minima che sarebbe trattiva o compressiva ma non esiste o meglio è trascurabile e in ultimo la sigma massima in direzione radiale. Se il cubetto è sulle direzioni principali di tensione le Tau non possono esistere per il teorema di Cauchy.

$“Major principal value”$ si riferisce alla tensione massima in modulo. Questo è uno stato tensionale praticamente piano anche se esiste quel piccolissmo contributo eliminabile raffinando la mesh. In futuro quindi potremo analizzare una sola porzione del modello per l’analisi e lo studio della sua interezza, questo è possibile se esso è simmetrico a due assi. Inoltre sullo spessore, il modello avrà un solo elemento e dovrà essere un “Modello settore”. Appongo dunque i vincoli di simmetria. Il piano di simmetria è l’innalzamento dell’asse di simmetria in direzione ortogonale a se stesso, inoltre esso possiede una direzione normale e due tangenziali. La simmetria geometrica della struttura impone che un punto da una parte del piano di simmetria possegga le stesse proprietà di un punto giacente sul lato opposto ad esso. Se i vincoli e i carichi sono anch’essi simmetrici il problema nasce definito simmetrico e se il sistema si comporta linearmente anche la risposta sarà simmetrica. Quindi possiamo analizzare solo metà perché lo stato tensionale dell’altra metà lo recupero per simmetria.

Per le antisimmetrie vedi schema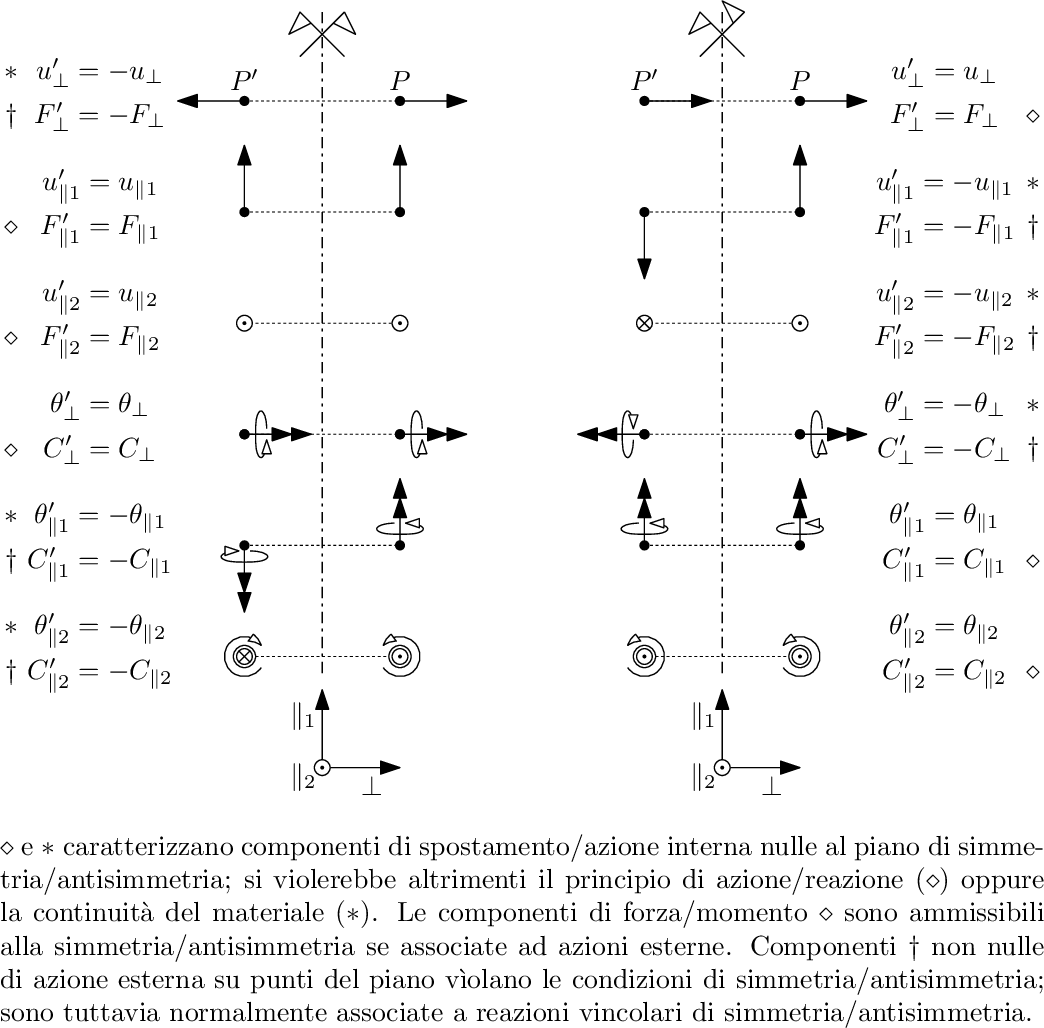

modello a fine lezione tubo_3d_v002.mud