Indice
Codice FEM Fortran autocostruito
Intro
Cos'è un Sottoprogramma (Subroutine)?
Il linguaggio di programmazione FORTRAN consente di suddividere le operazioni tramite sottoprogrammi che ritornano un risultato al programma chiamante, sviluppando un approccio top-down. L'utilizzo dei sottoprogrammi è molto utile quando si deve ripetere una stessa operazione più volte, evitando così tutte le volte di copiare e incollare nel programma principale la stessa operazione. Questi sottoprogrammi possono essere del tipo FUNZIONI oppure SUBROUTINE. Funzioni e subroutine devono avere nome univoco e per il resto sono indipendenti dal programma che le ha richiamate. Il costrutto FUNZIONE restituisce un singolo valore scalare, motivo per cui spesso si ricorre al costrutto SUBROUTINE. A differenza dei programmi che terminano con “ stop end”, i sottoprogrammi terminano con “return end”. Nel sottoprogramma le etichette sono autonome perciò per dichiarare le variabili locali, si possono utilizzare etichette aventi stesso nome e tipologia di quelle già dichiarate nel programma principale (MAIN). Programma e sottoprogramma comunicano inviandosi indirizzi di memoria perciò è fondamentale che comunichino con la stessa tipologia di elementi: in particolare il programma invia i parametri passati al sottoprogramma che restituisce un valore.
Subroutine Forces
Concludiamo con l'analisi del codice della lezione precedente. Avevamo anticipato qualcosa
 riguardo l'assemblaggio del vettore delle forze (termini noti).
riguardo l'assemblaggio del vettore delle forze (termini noti).
Andiamo a rivedere la subroutine FORCES:

questa prende in input:
- IFMAX : il numero di nodi sui quali è definita la forza concentrata;
- IFXY : un vettore di elementi interi che definisce l'indice del nodo su cui è applicato il 1°, 2° ,3° ecc. carico concentrato applicato;
- FXY : matrice di (2, IFMAX) 2 righe e IFMAX colonne, e contiene nella prima riga le componenti di forza concentrata in direzione x e nella seconda le componenti di forza concentrate in direzione y;
- NODES : numero di nodi della struttura e serve principalmente a definire la dimensione del vettore FORCE che contiene il termine noto dell'equazione di equilibrio del sistema;
- FORCE : vettore dei termini nodi che contiene 2*NODES elementi, dove 2 è il numero di gdl al nodo.
Abbiamo poi un ciclo DO che scorre sul IFMAX-esimo nodo caricato, definendo il gdl globale associato allo spostamento (o forza) x [*2-1] o y [*2] del nodo considerato.
Andiamo sul vettore dei termini noti, sulla posizione associata al gdl x definiamo il contenuto della cella alla posizione INDX del vettore dei termini noti FORCE, lo defniamo come elemento (1,I10) prima riga, colonna I10-esima ( con I10 che scorre sui nodi caricati) di carico concentrato definito dall'input utente.
Stessa cosa per la componente INDY del vettore delle forze, è definita uguale al carico in y fornito dall'utente sul corrispettivo nodo caricato.
Se vogliamo fare un confronto aprendo il file mesh_tria_comp.dat i nodi caricati sono:
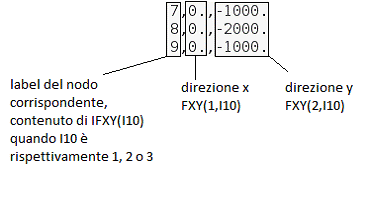
se I10=2 uso la seconda terna di dati, per I10=3 passerò alla terza terna.
Da qualche altra parte, al di fuori di questa subroutine, il vettore FORCES viene inizializzato a valori nulli perchè in questa subroutine vengono definiti i termini del vettore FORCE solo ove non sono nulli, quindi ci sarà una SUBROUTINE CLEAR chiamata sul vettore FORCE e li verrà azzerato il vettore, per poi andare a definire tutti i termini non nulli dentro al vettore dei carichi esterni.
 Ovviamente sarebbe molto più leggibile il codice se questo call clear fosse stato inserito dentro la subroutine che crea il vettore FORCE.
Ovviamente sarebbe molto più leggibile il codice se questo call clear fosse stato inserito dentro la subroutine che crea il vettore FORCE.
Subroutine Cnstng
La SUBROUTINE successiva CNSTNG, definisce il vincolamento.
 Prende in input una matrice [ ICNXY (2, ICNMAX) ] di 2 righe e ICNMAX (numero di nodi vincolati) come numero di colonne. ICNXY ha due righe, la prima contiene il label del nodo vincolato.
Prende in input una matrice [ ICNXY (2, ICNMAX) ] di 2 righe e ICNMAX (numero di nodi vincolati) come numero di colonne. ICNXY ha due righe, la prima contiene il label del nodo vincolato.
Ad esempio nel nostro caso dal file mesh_tria_comp.dat la parte di file input che viene usata per riempire ICNXY e CNXY è :
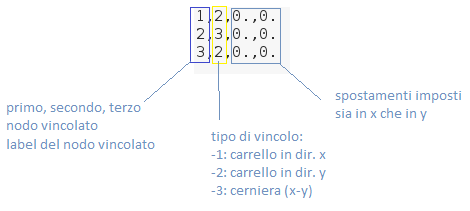
ovviamente lo spostamento in x quando utilizziamo un carrello in dir. y non viene utilizzato.
Questa subroutine parte come un selettore, innanzi tutto c'è un ciclo DO che scorre sui nodi vincolati ( I10=1, ICNMAX ) e si va a fare un test, si va a vedere cosa c'è scritto sulla seconda riga di ICNXY in corrispondenza dello specifico vincolo.
Il 2 presente in ICNXY, specifica che il parametro che deve essere considerato è la seconda riga, ovvero quella corrispondente al tipo di vincolo da applicare, che può essere 1, 2 o 3 a seconda che si tratti di un carrello in direzione x, un carrello in direzione y oppure una cerniera. E qui il codice si triforca, se uguale a 1, 2 o 3 salta rispettivamente alle funzioni 100, 200 o 300.
Nel nostro caso il primo nodo vincolato è il nodo con label 1 e lo specifico vincolo è il 2, quindi quando I10=1 si tratta del primo nodo vincolato, trovo nella matrice un 2 e in questo caso salto alla parte di codice con label 200. Nel caso del secondo nodo vincolato , trovo 3, quindi si salterà alla parte di codice con label 300.
Se non salto a 100, 200 o 300 allora il termine ICNXY non vale ne 1, ne 2, ne 3, la cosa non è prevista dal codice e quindi questo emetterà un segnale d'errore e semplicemente STOP, si ferma, restituendo il controllo al terminale. Se invece rientra in uno di questi tre casi si salterà alla parte di codice corrispondente;
Vincolamento con carrello in direzione x
Vediamo nel dettaglio cosa succede se rientro nel caso 1 con vincolamento in direzione x
 Prima cosa, si va a ricavare il g.d.l. associato al vincolo specifico, in particolare stiamo parlando dello spostamento in dir. X di un nodo, il nodo è quello che trovo nella matrice ICNXY(1, I10) riga 1 colonna I10 [che nel caso specifico è il nodo 1, il primo dei tre nodi vincolati].
Prima cosa, si va a ricavare il g.d.l. associato al vincolo specifico, in particolare stiamo parlando dello spostamento in dir. X di un nodo, il nodo è quello che trovo nella matrice ICNXY(1, I10) riga 1 colonna I10 [che nel caso specifico è il nodo 1, il primo dei tre nodi vincolati].
Numero del nodo*2-1 è la mappatura usata per costruire il vettore delle incognite ed è il g.d.l dello spostamento lungo x del nodo 1. Una volta identificato questo primo g.d.l INDX vado a scorrere, tramite ciclo DO con un indice I110 che va da 1 a 2*NODES, quindi scorre su tutti i g.d.l.
Successivamente si opera sulla matrice rigidezza , STRUTK, che ha riga associata al g.d.l ( INDX ) da vincolare, e colonna I110 che scorre su tutti i g.d.l. Tutti gli elementi della INDX-esima riga associata ai g.d.l da vincolare vengono posti = 0 .
E quindi questa istruzione ripetuta all'interno di questo ciclo DO 110 annulla totalmente la riga associata al g.d.l da vincolare. Dopodiché trasferisco sul vettore dei termini noti ( FORCE(I110) ) tutti i termini della INDX-esima colonna della matrice rigidezza moltiplicati per il valore impostato del vincolo.
Da notare che FORCE(I110) è di volta in volta il primo elemento fino al 2*NODES-esimo elemento di FORCE e viene ridefinito come se stesso meno l'elemento che trovo alla colonna INDX-esima della matrice rigidezza, e riga che scorre coerentemente con l'elemento di FORCE su cui vado a operare. Moltiplicata per CNXY ( 1, I10) il valore imposto su quel g.d.l.
[Nel nostro caso è un valore imposto di spostamento nullo 0. , ma potrebbe essere anche uno spostamento non omogeneo, ad es. impongo che un certo nodo si muova di 1mm ( o di una quantità a piacere)].
Effettuata la moltiplicazione, questa roba viene combinata con quello che era presente precedentemente nel vettore FORCE, quindi implemento il fatto che il termine noto è uguale a se stesso meno la colonna associata al g.d.l della matrice rigidezza per lo spostamento imposto. Dopo aver trasferito al termine noto il contenuto di un dato termine della INDX-esima colonna della matrice rigidezza su quel termine scrivo uno zero quindi annullo il termine, sarebbe un brutto errore invertire le due operazioni, prima uso il valore che trovo nella cella della colonna poi annullo la cella, se prima annullo e poi scrivo quello che c'è nella cella è chiaro che trovo tutti zeri.
Successivamente:
 finite le operazioni che richiedono un ciclo, vado a scrivere dunque 1 sul termine diagonale della matrice di rigidezza e vado a scrivere lo spostamento imposto sull'INDX-esimo g.d.l del vettore dei termini noti. Ripetiamo, il vettore termine noto a questo a questo punto non è più un vettore di forze ma un vettore misto. Dopo aver operato correttamente e fatto tutte le operazioni necessarie per applicare un carrello in dir. X posso procedere con il comando GO TO 10 verso la fine della procedura, dove si nota che proprio 10 anticipa i comandi RETURN ed END.
finite le operazioni che richiedono un ciclo, vado a scrivere dunque 1 sul termine diagonale della matrice di rigidezza e vado a scrivere lo spostamento imposto sull'INDX-esimo g.d.l del vettore dei termini noti. Ripetiamo, il vettore termine noto a questo a questo punto non è più un vettore di forze ma un vettore misto. Dopo aver operato correttamente e fatto tutte le operazioni necessarie per applicare un carrello in dir. X posso procedere con il comando GO TO 10 verso la fine della procedura, dove si nota che proprio 10 anticipa i comandi RETURN ed END.

Vincolamento con carrello in direzione y
Stessa cosa se il vincolo è un carrello in dir. Y semplicemente al posto di INDX ( g.d l in x associato a un dato nodo ) utilizzeremo INDY che è il g.d.l y associato al suddetto noto e la costruzione è sostanzialmente analoga:
 uniche differenze sono il fatto che vado a prendere da CNXY(2,I10) invece del primo elemento che è lo spostamento in x imposto, prendo la seconda riga che contiene gli spostamenti y imposti.
uniche differenze sono il fatto che vado a prendere da CNXY(2,I10) invece del primo elemento che è lo spostamento in x imposto, prendo la seconda riga che contiene gli spostamenti y imposti.
Ricordiamo che si hanno più vincoli, l'applicazione del secondo vincolo della lista avviene sulla matrice già modificata dall'applicazione del primo vincolo e l'applicazione del terzo avviene su una matrice che è già stata modificata dall'applicazione del 1° e 2° vincolo. Quindi i vincoli vengono applicati in successione e tutti finiscono sulla stessa matrice di rigidezza e sul vettore dei termini noti.
Se la procedura è ben definita cambiando l'applicazione dei vincoli non dovrebbe cambiare la matrice rigidezza o il vettore dei termini noti, ottenuti a fine vincolamento.
Vincolamento con cerniera
Ultimo caso, la cerniera, semplicemente sarà la combinazione dell'applicazione dei due casi precedenti, i codici saranno copiati. Unico passaggio da attenzionare 

Subroutine Vincola
Quindi la SUBROUTINE CNSTNG
sostanzialmente implementa il vincolamento in 3 ipotesi, carrello x, carrello y e cerniera, se volessimo qualcosa di più semplice e leggibile, è stata creata una nuova SUBROUTINE 'vincola' che vincola un generico g.d.l senza preoccuparsi realmente se si tratta di uno spostamento x o y.
 In pratica prende in input:
In pratica prende in input:
- la matrice STRUTK;
- N ( n°di g.d.l pari a 2*NODES);
- FORCES ( il vettore dei termini noti );
- (g.d.l da vincolare);
- V (valore specifico).
Presenta un ciclo DO con l'indice J che scorre genericamente su tutti i g.d.l.
Per J=1, N provvedo ad annullare l'elemento che sta sulla riga I colonna J ( riga associata al g.d.l vincolato, colonna con J che scorre, ovvero annullo tutta la riga).
A questo punto il termine diagonale della riga lo pongo = 1 e la componente I-esima del vettore dei termini noti = allo spostamento imposto V.
Avendo già sistemato FORCE ( I ) = V il valore per il termine I-esimo del vettore dei termini noti, non vorrò più operare su quell'oggetto che ho già definito in maniera esatta, quindi faccio due cicli uno con J che va da 1 a I-1, quindi tutta la parte pre-g.d.l I-esimo, mentre il secondo ciclo va, dall'elemento successivo all'I-esimo “I+1” all'ultimo, questi due cicli eseguono la stessa istruzione, si ridefinisce l'elemento J-esimo del vettore dei termini noti come se stesso meno il contributo preso dalla matrice rigidezza moltiplicati per il valore imposto a termine noto. Dopo di ciò annullo il termine sulla colonna della matrice di rigidezza ripristinando la simmetria perché avevo precedentemente annullato i termini diagonali della matrice. E così ottengo lo stesso effetto, unica cosa questo procedimento lo eseguo sul generico g.d.l, avendo a disposizione la subroutine 'vincola' la subroutine CNSTNG si riduce di molto, nel senso che ci sono sempre i 3 casi, le tre forme di CALL diverse della subroutine 'vincola'.
Subroutine Gauss
Una volta che ho assemblato la matrice rigidezza e l'ho vincolata posso passare alla procedura di soluzione. Non mi resta che chiamare il solutore di equazioni lineari ( CALL GAUSS ) , grazie al quale otterremo i risultati per soluzione Gaussiana, triangolarizzando la matrice di sistema e poi risolvendola.
N.B. Non implementare mai questo tipo di risolutore, lo hanno fatto altri con più esperienza, basta copiare/incollare il codice altrui, ma dove troviamo questi risolutori?
Esistono molteplici librerie di codice, ad esempio:
- LAPACK ' Linear Algebra Package';
- BLAS ' Basic Linear Algebra Subprograms'.
Le Blas sono operazioni più semplici come definizione di una matrice come combinazione lineare di altre 2. Si suddividono in 3 LEVEL in dipendenza del peso computazionale delle stesse operazioni.
Una volta lanciato CALL GAUSS questo restituirà il vettore degli spostamenti nodali incogniti UV. CALL GAUSS prende per input:
- 2*NODES : i g.d.l;
- STRUTK : la matrice di rigidezza;
- FORCES : il vettore dei termini noti;
e restituisce in output: UV : vettore contenente gli spostamenti nodali in x e y;
Postprocessor
A questo punto ho finito di risolvere il mio sistema, ho trovato dei valori specifici per le incognite, quindi comincio ad emettere fine di output con i risultati. Quindi parto con le istruzioni WRITE che scrivono sull'unità 2 ( WRITE (2,*)) che è un file di output che abbiamo precedentemente aperto, notare all'inizio del codice il comando:
 ovvero apri come unità 2 il file che ha questo, lo status unknown vuol dire “se non esiste lo creo se esiste lo sovrascrivo”.
ovvero apri come unità 2 il file che ha questo, lo status unknown vuol dire “se non esiste lo creo se esiste lo sovrascrivo”.
Comincio a scrivere sui file di output per I20 che va dal 1° all' n-esimo nodo;
- I20 : il numero del nodo
- UV(I20*2-1) : lo spostamento lungo x con gdl I20*2-1
- UV(I20*2) : lo spostamento lungo y con gdl I20*2
 Trovati gli spostamenti si potrebbe andare a calcolare le tensioni, che magari ci interessano;
Trovati gli spostamenti si potrebbe andare a calcolare le tensioni, che magari ci interessano;
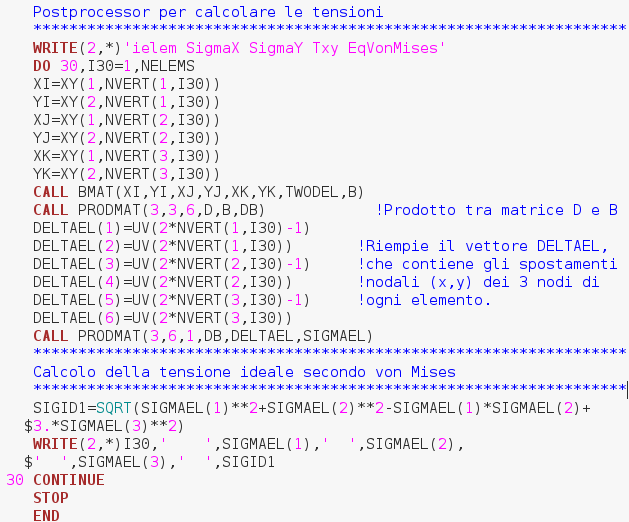
Allora scrivo a video che seguiranno i valori tensionali. Ho un ciclo DO che scorre sugli elementi in questo ciclo che si chiude come tutti i cicli do con il numero ( label ) corrispondente seguito da continue. Vado a ricavare le coordinate x ( per ogni specifico elemento, quindi per ogni elemento dell'I30-esimo elemento) del nodo I, le coordinate x del nodo J, e coordinate x del nodo K e le corrispettive di y andando a pescare sulla riga e colonna opportura nella matrice XY che ha come prima riga le coordinate x e seconda le coordinate y, nella colonna associata all'opportuno nodo lo vado a prendere dalla matrice NVERT che contiene per ogni elemento il label del 1°, 2°, 3° elemento, perché stiamo andando a calcolare quei nodi. Per lo specifico elemento ne calcoliamo la matrice B da CALL BMAT (che manda in output proprio la matrice B) che lega spostamenti e deformazioni. Successivamente si calcolerà la matrice DB prodotto della matrice di legame costitutivo D , supposta uniforme per tutti gli elementi, e della specifica matrice B calcolata precedentemente per ogni singolo elemento. Questa matrice DB moltiplicata per un vettore di 6 elementi che contiene spostamento in x del nodo 1 locale d'elemento, spostamento in y del nodo 1 locale d'elemento, e così via per i nodi locali d'elemento 2 e 3, sono 6 gdl che mi daranno i valori tensionali sull'elemento. Vado a comporre questo vettore di 6 elementi che contiene gli spostamenti ai gdl dei nodi dello specifico elemento:
1° elemento di DELTAEL ( vettore degli spostamenti sull'elemento) è uguale a UV (vettore degli spostamenti di struttura) preso al gdl opportuno e così via.
Si procede con un prodotto tra matrice e vettore ( DELTAEL qui è un vettore, ma ha solo un indice quindi solo una dimensione), quando si usa questo prodotto matrice vettore implicitamente siamo supponendo che DELTAEL diventa un vettore colonna.
Il vettore SIGMAEL che è di 3 elementi conterrà come primo elemento la sigma x, come secondo elemento la sigma y e come terzo la tau xy. Prima di scrivere a video queste quantità, vado a calcolare la tensione ideale (equivalente) secondo Von Mises SIGID1 , come:
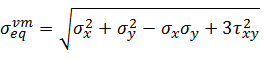 e questa è la tesione ideale secondo Von Mises.
e questa è la tesione ideale secondo Von Mises.
Infine : WRITE(2,*) : stampo a video l'indice dell'elemento (I30), il valore della tensione in x [SIGMAEL(1)], il valore della tensione in y [SIGMAEL(2)], della tau_xy [SIGMAEL(3)] e poi la tensione ideale secondo Von Mises [SIGID1]. Faccio questo per ogni elemento, dopo di che, STOP, END e ho finito l'esecuzione del mio codice agli elementi finiti.
Possiamo a questo punto lanciare il programma da terminale con il comando:

Analisi dei risultati
Ricordiamo di seguito la struttura analizzata in partenza:

Il carico distribuito applicato alla struttura può essere pensato come applicato concentrato sui nodi utilizzando una riduzione secondo aree di influenza.
Lo spessore della struttura non è considerato in questo codice, quindi ogni risultato è normalizzato a spessore unitario.
 La cerniera applicata nel nodo 2 è soggetta ad una reazione vincolare nulla lungo l'asse x, ma è necessaria per evitare una traslazione indefinita dell'intera struttura lungo la medesima direzione nell'implementazione del codice.
La cerniera applicata nel nodo 2 è soggetta ad una reazione vincolare nulla lungo l'asse x, ma è necessaria per evitare una traslazione indefinita dell'intera struttura lungo la medesima direzione nell'implementazione del codice.
La cerniera del sistema trattato rappresenta un vincolo di posizionamento: questi vincoli non prendono carico teoricamente, ma nell'implementazione numerica compensano gli inevitabili errori di troncamento presenti (matematicamente servono a rendere il rango della matrice del sistema pieno, cioè la matrice stessa del sistema non singolare e quindi il sistema univocamente determinato).
I risultati restituiti dal programma Fortran autocostruito sono i seguenti:

Spostando il vincolo di posizionamento in un diverso nodo, lo stato tensionale non cambia, mentre la soluzione degli spostamenti nodali differisce di un moto di corpo rigido.
 Gli spostamenti nodali con ordine di grandezza di almeno 7 volte inferiore a quello della norma del vettore degli spostamenti nodali sono da considerarsi nulli; la restituzione da parte del programma di un risultato numerico, sebbene molto piccolo, è da imputarsi ad errori di calcolo o arrotondamento.
Gli spostamenti nodali mostrano come la struttura, sottoposta al carico, si abbassi e si allarghi per effetto Poisson (gli spostamenti lungo x valgono 0,3 volte gli spostamenti lungo y, proprio come previsto per un acciaio).
Le reazioni vincolari non vengono calcolate dal programma: cioè è dovuto al fatto che la matrice rigidezza pre-vincolamento (necessaria per il calcolo delle reazioni vincolari) non è stata mantenuta in memoria, bensì sovrascritta durante il calcolo.
Gli spostamenti nodali con ordine di grandezza di almeno 7 volte inferiore a quello della norma del vettore degli spostamenti nodali sono da considerarsi nulli; la restituzione da parte del programma di un risultato numerico, sebbene molto piccolo, è da imputarsi ad errori di calcolo o arrotondamento.
Gli spostamenti nodali mostrano come la struttura, sottoposta al carico, si abbassi e si allarghi per effetto Poisson (gli spostamenti lungo x valgono 0,3 volte gli spostamenti lungo y, proprio come previsto per un acciaio).
Le reazioni vincolari non vengono calcolate dal programma: cioè è dovuto al fatto che la matrice rigidezza pre-vincolamento (necessaria per il calcolo delle reazioni vincolari) non è stata mantenuta in memoria, bensì sovrascritta durante il calcolo.
Appendice: Librerie esterne LAPACK e BLAS
Esistono in rete delle librerie di riferimento in cui è possibile trovare molti programmi svolti.
Le più famose sono:
- LAPACK (Contiene operazioni matriciali, calcolo di rango, determinante ecc.);
- BLAS (contenente operazioni matriciali).
LAPACK (Linear Algebra PACKage) è un insieme di librerie software usate per effettuare calcoli scientifici ad alto livello. Tali librerie sono state scritte in Fortran 77 e sono di dominio pubblico, anche se esistono delle personalizzazioni di queste librerie a pagamento. L'ultima versione è la 3.5.0 del 16 novembre 2013. Mediante queste librerie, è possibile effettuare calcoli di notevole importanza, come il calcolo di autovalori ed autovettori di matrici, risoluzione di sistemi lineari, fattorizzazioni di matrici, e molto altro ancora. Ad esempio, esistono delle procedure interne, nascoste all'utente, in grado di trasformare la matrice iniziale in una matrice tridiagonale, per poi calcolare effettivamente autovalori ed autovettori. Come dipendenza questa libreria richiede l'installazione di un'altra libreria: la BLAS (Basic Linear Algebra Subprograms). Le procedure all'interno di tale libreria consentono di effettuare calcoli scientifici di più basso livello, come il calcolo del prodotto scalare tra due vettori, prodotto matrice per vettore, etc.
BLAS (Basic Linear Algebra Subprograms) sono routine standard che forniscono elementi di base per l’esecuzione delle operazioni su vettori e matrici. Il Livello 1 di BLAS esegue operazioni scalari, vettoriali e vettore-vettore, il Livello 2 di BLAS esegue operazioni matrice-vettore, e il Livello 3 di BLAS risolve operazioni matrice-matrice. Poiché BLAS risulta particolarmente efficiente, portatile, e ampiamente disponibile, è comunemente usata per lo sviluppo di software di algebra lineare di alta qualità.
Esempio di utilizzo librerie Lapack, che utilizza la subroutine ZGEEV:
Program Eigenvalue
c finding the eigenvalues of a complex matrix using LAPACK
Implicit none
c declarations, notice double precision
complex*16 A(3,3), b(3), DUMMY(1,1), WORK(6)
integer i, ok
c define matrix A
A(1,1)=(3.1, -1.8)
A(1,2)=(1.3, 0.2)
A(1,3)=(-5.7, -4.3)
A(2,1)=(1.0, 0)
A(2,2)=(-6.9, 3.2)
A(2,3)=(5.8, 2.2)
A(3,1)=(3.4, -4.0)
A(3,2)=(7.2, 2.9)
A(3,3)=(-8.8, 3.2)
c c find the solution using the LAPACK routine ZGEEV
call ZGEEV('N', 'N', 3, A, 3, b, DUMMY, 1, DUMMY, 1, WORK, 6,
$WORK,ok)
c c parameters in the order as they appear in the function call c no left eigenvectors, no right eigenvectors, order of input matrix A, c input matrix A, leading dimension of A, array for eigenvalues, c array for left eigenvalue, leading dimension of DUMMY, c array for right eigenvalues, leading dimension of DUMMY, c workspace array dim>=2*order of A, dimension of WORK c workspace array dim=2*order of A, return value c c output of eigenvalues
if (ok .eq. 0) then
do i=1, 3
write(*,*) b(i)
enddo
else
write (*,*) "An error occured"
endif
end
Compilare il codice di cui sopra,con il seguente comando(previa installazione delle librerie lapack):
gfortran provalapack.for -llapack && ./a.out
Nota: quando utilizziamo delle librerie esistenti bisogna stare attenti a tutte le variabili e subroutine definite ma che sono sovrabbondanti per i nostri scopi, quindi si preferisce richiamare il programma già compilato con il comando call.
Nel nostro esempio si può vedere nella subroutine ZGEEV le molteplici variabili che sono definite: http://www.netlib.org/lapack/explore-3.1.1-html/zgeev.f.html
Questo è il file dell'esempio visto che trova gli autovalori di una matrice complessa:provalapack http://www.physics.orst.edu/~rubin/nacphy/lapack/codes/eigen-f.html
Stat
| Autore | Time_part |
|---|---|
| F_S | a |
| G_M | a |
| M_G | a |
| MD_R | a |
| Riga_tot |

Comando per lanciare mentat mentat2013.1 -ogl -glflush



Discussione
REVISORE 1:
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
Tutte le immagini e le formule rispettano le regole di composizione
Il testo proposto è coerente con gli appunti personali del revisore?
Sì è coerente
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
Non sono necessarie ulteriori figure
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
Ritengo che si possano preparare gli argomenti sulla base di questi appunti essendo molto ricchi e contenedo tutte le informazioni necessarie.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
No non è necessario
Varie ed eventuali.
Spazio per eventuali note destinate al solo curatore (da non comunicarsi agli autori).
Ore dedicate a questa revisione
1 h.