Indice
Trasformazioni della matrice di rigidezza
La matrice di rigidezza K di una struttura non necessita di essere memorizzata interamente sulla memoria del calcolatore: essa infatti è quadrata e simmetrica, pertanto si può memorizzare anche solo la parte sopra (o sotto) diagonale, risparmiando potenzialmente quasi metà della memoria. Esistono tuttavia anche altri metodi di memorizzazione, più utilizzati, che consentono di occupare il minor spazio possibile.
Si prenda come esempio una trave incastrata, discretizzata agli elementi finiti in 16 elementi isoparametrici quadrilateri a 4 nodi (quad4):
 Ognuno di questi elementi quad4 possiede 4 nodi, a ciascuno dei quali deve essere associato uno spostamento in direzione x (u) e in direzione y (v): nel complesso, quindi, ad ognuno di questi quadrilateri verrà associata una matrice $K_{el}$ di ordine 8 (con 64 elementi), i cui elementi possono anche essere tutti non nulli. In generale, quindi, gli elementi non nulli sono 16*64=1024. Tali elementi di tutte queste matrici dovranno poi essere assemblati sulla matrice K globale della struttura, che essendo di ordine 54 (come il numero di nodi presenti) conterrà 54*54=2916 elementi. Si vuole ora ridurre questo numero per evitare di memorizzarli tutti: bisogna infatti considerare che sono presenti molti zeri, per i quali non vale la pena di allocare memoria sul calcolatore.
Ognuno di questi elementi quad4 possiede 4 nodi, a ciascuno dei quali deve essere associato uno spostamento in direzione x (u) e in direzione y (v): nel complesso, quindi, ad ognuno di questi quadrilateri verrà associata una matrice $K_{el}$ di ordine 8 (con 64 elementi), i cui elementi possono anche essere tutti non nulli. In generale, quindi, gli elementi non nulli sono 16*64=1024. Tali elementi di tutte queste matrici dovranno poi essere assemblati sulla matrice K globale della struttura, che essendo di ordine 54 (come il numero di nodi presenti) conterrà 54*54=2916 elementi. Si vuole ora ridurre questo numero per evitare di memorizzarli tutti: bisogna infatti considerare che sono presenti molti zeri, per i quali non vale la pena di allocare memoria sul calcolatore.
Memorizzazione in forma sparsa
Uno dei metodi più semplici per memorizzare la matrice di rigidezza si basa proprio sul fatto che essa è una matrice sparsa, cioè che contiene molti zeri. A differenza di una matrice piena, dunque, potrà essere tenuto conto soltanto degli elementi non nulli, memorizzati in un unico vettore: per riconoscere la posizione di questi numeri, ormai svincolati dalla matrice originaria, sarà però anche necessario affiancare a ciascun valore i suoi numeri di riga e di colonna, riportati in due vettori ulteriori. Si è così ridotta la matrice a un insieme di soli 3 vettori, di cui due interi (quelli di riga e colonna degli elementi) e uno reale o complesso a seconda del tipo di matrice:
| riga | colonna | Valore cella |
| 3 | 4 | 1.123 |
| 1 | 10 | -1.15 |
| … | … | … |
Nel caso della matrice K, considerando che è simmetrica, si potrà risparmiare altro spazio di memoria scrivendo i soli valori sopra (o sotto) diagonali. Questo metodo ha il vantaggio di essere semplice, ma presenta alcuni punti a sfavore. In primo luogo bisogna considerare che si sono aggiunti due vettori, quelli che riportano i numeri di riga e colonna degli elementi: questo rischia addirittura di peggiorare l'occupazione di memoria, se gli zeri della matrice di partenza sono troppi pochi. In secondo luogo, esistono dei processi che manipolano la matrice, modificandone il numero di zeri: un esempio è la trasformazione di una matrice in una triangolare superiore con il metodo di eliminazione gaussiana. Se i termini non nulli rischiano di aumentare, bisogna prevedere un'allocazione dinamica della memoria, che può sempre essere fatta ma certamente complica l'implementazione.
Memorizzazione in forma bandata
Un altro metodo di memorizzazione della matrice di rigidezza prevede di trasformarla prima in matrice bandata e successivamente allocare il solo spazio di memoria necessario a contenerla. Consideriamo l'elemento quad4 di nodi 1-4-5-2 della trave incastrata: a ciascun nodo locale sono associati 2 gradi di libertà (corrispondenti agli spostamenti in direzione x e y) i quali si calcolano rispettivamente come:
| $2l - 1$ | in direzione x |
| $2l$ | in direzione y |
dove l rappresenta il nodo locale.
Appare evidente che il grado di libertà minimo ha il valore 1 (dallo spostamento in direzione x del nodo 1) e quello massimo 10 (dallo spostamento in direzione y del nodo 5). In seguito, i termini della matrice di rigidezza di questo elemento quad4 verranno assemblati sulla matrice K complessiva: essi saranno dunque confinati in una sottomatrice quadrata che si estende dalla riga (e colonna) 1 alla riga (e colonna) 10
 Osserviamo ora il legame tra il vettore delle forze applicate ai nodi e il vettore degli spostamenti nodali dell'elemento di trave, con la matrice $K_{el}$ come matrice dei coefficienti:
Osserviamo ora il legame tra il vettore delle forze applicate ai nodi e il vettore degli spostamenti nodali dell'elemento di trave, con la matrice $K_{el}$ come matrice dei coefficienti:
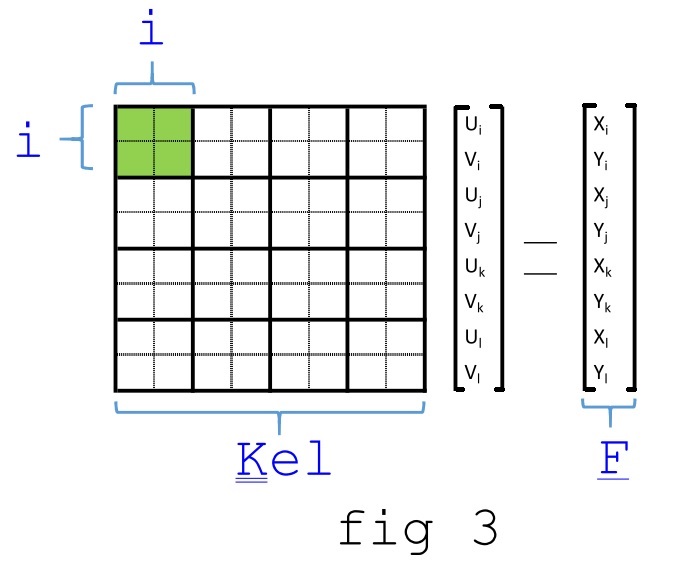 In $K_{el}$, per esempio, il blocco 2×2 corrispondente alle prime due righe e colonne (di indici locali i e i) definisce le forze ($X_{i}$ e $Y_{i}$) che occorre applicare al nodo i per equilibrare le reazioni elastiche associate agli spostamenti ui e vi.
In $K_{el}$, per esempio, il blocco 2×2 corrispondente alle prime due righe e colonne (di indici locali i e i) definisce le forze ($X_{i}$ e $Y_{i}$) che occorre applicare al nodo i per equilibrare le reazioni elastiche associate agli spostamenti ui e vi.
 Denominato F il vettore delle forze esterne, questo prodotto matrice per vettore può essere riscritto così:
$$
\textbf{K}_{el *,1}*u_{i} + \textbf{K}_{el *,2}*v_{i} + ... + \textbf{K}_{el *,8}*v_{l} = \textbf{F}
$$
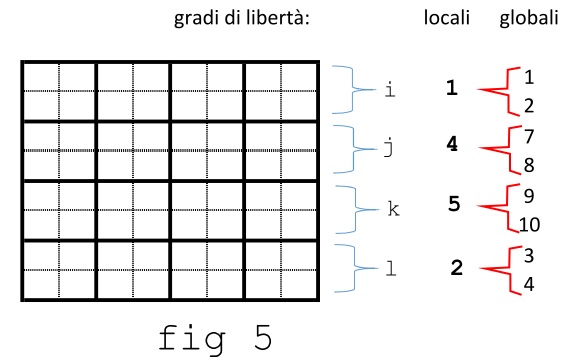
ovvero come somma di prodotti tra ogni colonna della matrice (l'asterisco nel pedice indica scorrimento su tutte le righe) per le specifiche componenti del vettore degli spostamenti nodali. Come esempio, si può dire che la terza colonna di $K_{el}$ rappresenti le forze che bisogna applicare ai 4 nodi per equilibrare uno spostamento $u_{j}=1$ (e tutte le altre componenti nulle). Si può infine dare questa interpretazione: le colonne di $K_{el}$ sono associate ai singoli gradi di libertà (ovvero gli spostamenti nodali imposti), mentre ogni riga è associata a una componente di forza nodale. Se ora si considera, ad esempio, l'elemento di posto (4,6) di $K_{el}$, esso va assemblato sulla matrice K globale nel posto (8,10): facendo lo stesso per ogni altro elemento, risulta evidente che nessuno di essi verrà assemblato in K in un posto con indice di riga o colonna superiore al 10,vedi figura 2. La corrispondenza tra gradi di libertà locali e globali è indicata sulla matrice $K_{el}$ in questa figura:
Denominato F il vettore delle forze esterne, questo prodotto matrice per vettore può essere riscritto così:
$$
\textbf{K}_{el *,1}*u_{i} + \textbf{K}_{el *,2}*v_{i} + ... + \textbf{K}_{el *,8}*v_{l} = \textbf{F}
$$
ovvero come somma di prodotti tra ogni colonna della matrice (l'asterisco nel pedice indica scorrimento su tutte le righe) per le specifiche componenti del vettore degli spostamenti nodali. Come esempio, si può dire che la terza colonna di $K_{el}$ rappresenti le forze che bisogna applicare ai 4 nodi per equilibrare uno spostamento $u_{j}=1$ (e tutte le altre componenti nulle). Si può infine dare questa interpretazione: le colonne di $K_{el}$ sono associate ai singoli gradi di libertà (ovvero gli spostamenti nodali imposti), mentre ogni riga è associata a una componente di forza nodale. Se ora si considera, ad esempio, l'elemento di posto (4,6) di $K_{el}$, esso va assemblato sulla matrice K globale nel posto (8,10): facendo lo stesso per ogni altro elemento, risulta evidente che nessuno di essi verrà assemblato in K in un posto con indice di riga o colonna superiore al 10,vedi figura 2. La corrispondenza tra gradi di libertà locali e globali è indicata sulla matrice $K_{el}$ in questa figura:
 Ripetendo lo stesso ragionamento per l'elemento di trave con nodi 19-22-23-20:
Ripetendo lo stesso ragionamento per l'elemento di trave con nodi 19-22-23-20:
 si osserva che ad esso sono associati altri 8 gradi di libertà, di cui quello di valore minore è 37 (dato da 19*2-1) e quello di valore maggiore è 46 (dato da 23*2): i termini della sua matrice $K_{el}$ verranno dunque assemblati su K in una sottomatrice che si estende tra le righe (e colonne) 37 e 46 e nessun elemento avrà indici di riga o colonna minori di 37 o maggiori di 46:
si osserva che ad esso sono associati altri 8 gradi di libertà, di cui quello di valore minore è 37 (dato da 19*2-1) e quello di valore maggiore è 46 (dato da 23*2): i termini della sua matrice $K_{el}$ verranno dunque assemblati su K in una sottomatrice che si estende tra le righe (e colonne) 37 e 46 e nessun elemento avrà indici di riga o colonna minori di 37 o maggiori di 46:
 Ripetendo questo procedimento per ogni matrice di rigidezza di tutti gli elementi quad4, si ottiene che i loro termini vengono assemblati su K in sottomatrici quadrate centrate sulla diagonale principale di K: si è ottenuta pertanto una struttura a banda, con i valori fuori dalla banda che sono tutti nulli:
Ripetendo questo procedimento per ogni matrice di rigidezza di tutti gli elementi quad4, si ottiene che i loro termini vengono assemblati su K in sottomatrici quadrate centrate sulla diagonale principale di K: si è ottenuta pertanto una struttura a banda, con i valori fuori dalla banda che sono tutti nulli:
 Ora si può procedere all'effettiva memorizzazione della matrice di rigidezza di struttura, con notevole risparmio di spazio di memoria (anche considerando la simmetria della matrice).
Il primo passo è calcolare la massima distanza degli elementi diversi da zero dalla diagonale principale, ovvero la larghezza di banda: essa, per una generica matrice, vale 1 se la matrice è diagonale, 2 se gli elementi non nulli sono anche nei posti immediatamente a sinistra e/o destra della diagonale ecc. Data la mesh, la larghezza di banda si può calcolare a priori: considerando di nuovo l'elemento di nodi 19-22-23-20 , chiamati $i_{min}=19$ e $i_{max}=23$, il grado di libertà minimo vale $i_{min}*2-1$ (qui 37), mentre quello massimo vale $i_{max}*2$ (qui 46).
Ora si può procedere all'effettiva memorizzazione della matrice di rigidezza di struttura, con notevole risparmio di spazio di memoria (anche considerando la simmetria della matrice).
Il primo passo è calcolare la massima distanza degli elementi diversi da zero dalla diagonale principale, ovvero la larghezza di banda: essa, per una generica matrice, vale 1 se la matrice è diagonale, 2 se gli elementi non nulli sono anche nei posti immediatamente a sinistra e/o destra della diagonale ecc. Data la mesh, la larghezza di banda si può calcolare a priori: considerando di nuovo l'elemento di nodi 19-22-23-20 , chiamati $i_{min}=19$ e $i_{max}=23$, il grado di libertà minimo vale $i_{min}*2-1$ (qui 37), mentre quello massimo vale $i_{max}*2$ (qui 46).
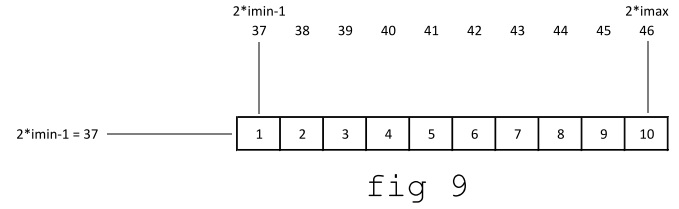 Risulta evidente che la larghezza di banda (b) in questo caso vale 10: la formula generale è
$$
b = 2*(i_{max}-i_{min}+1)
$$
Si vuole ora rappresentare K come matrice bandata: per questo scopo, la si rappresenta come matrice avente numero di righe uguale a quello della matrice originaria (che è anche il numero di gradi di libertà totali) e numero di colonne pari alla larghezza di banda b. In questa nuova matrice, il primo elemento di una generica riga i si trova in realtà sulla diagonale della matrice di partenza, cioé nel posto (i,i); il secondo si trova nel posto (i,i+1) ma anche in (i+1,i) per via della simmetria della matrice, e così via:
Risulta evidente che la larghezza di banda (b) in questo caso vale 10: la formula generale è
$$
b = 2*(i_{max}-i_{min}+1)
$$
Si vuole ora rappresentare K come matrice bandata: per questo scopo, la si rappresenta come matrice avente numero di righe uguale a quello della matrice originaria (che è anche il numero di gradi di libertà totali) e numero di colonne pari alla larghezza di banda b. In questa nuova matrice, il primo elemento di una generica riga i si trova in realtà sulla diagonale della matrice di partenza, cioé nel posto (i,i); il secondo si trova nel posto (i,i+1) ma anche in (i+1,i) per via della simmetria della matrice, e così via:
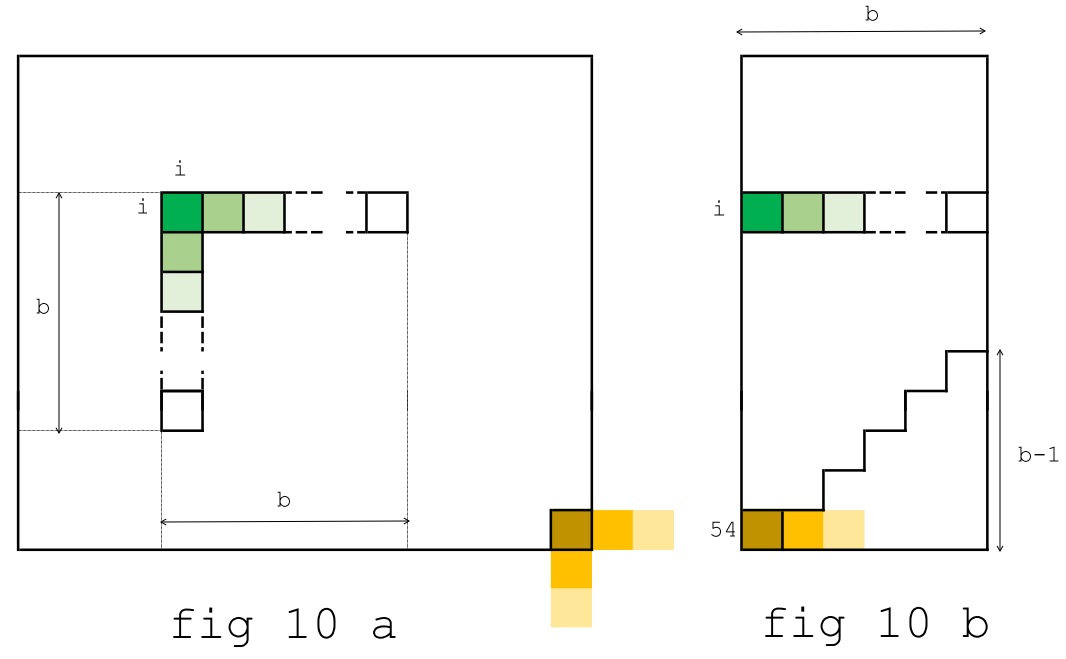 Il termine di posto (54,1) della matrice bandata occupa dunque la posizione (54,54) della vera matrice K, che è la sua ultima casella. Tutti gli altri elementi della riga 54 della matrice bandata, pertanto, non sono elementi della matrice di partenza: un problema simile si verifica per tutte le ultime b-1 righe della matrice bandata, come si vede in figura 10b.
Il termine di posto (54,1) della matrice bandata occupa dunque la posizione (54,54) della vera matrice K, che è la sua ultima casella. Tutti gli altri elementi della riga 54 della matrice bandata, pertanto, non sono elementi della matrice di partenza: un problema simile si verifica per tutte le ultime b-1 righe della matrice bandata, come si vede in figura 10b.
Lo spazio di memoria indicato, dunque, non viene utilizzato e potrebbe non essere allocato per la memorizzazione, ma questo complicherebbe la scrittura del codice di implementazione e quindi viene spesso tollerato.
Bisogna sottolineare che la larghezza di banda dipende strettamente da come si è effettuata la numerazione dei nodi della struttura: utilizzando la formula, si nota che la larghezza di banda cresce se in uno stesso elemento quad4 si trovano due nodi etichettati con numeri distanti tra loro. Il caso peggiore è quello in cui nello stesso elemento di struttura si trovano i numeri del primo e dell'ultimo nodo (corrispondenti al primo e ultimo grado di libertà), nel qual caso la larghezza di banda risulta essere esattamente quella della matrice di rigidezza piena.
 Le strutture peggiori dal punto di vista della larghezza di banda sono quelle chiuse su loro stesse:
Le strutture peggiori dal punto di vista della larghezza di banda sono quelle chiuse su loro stesse:
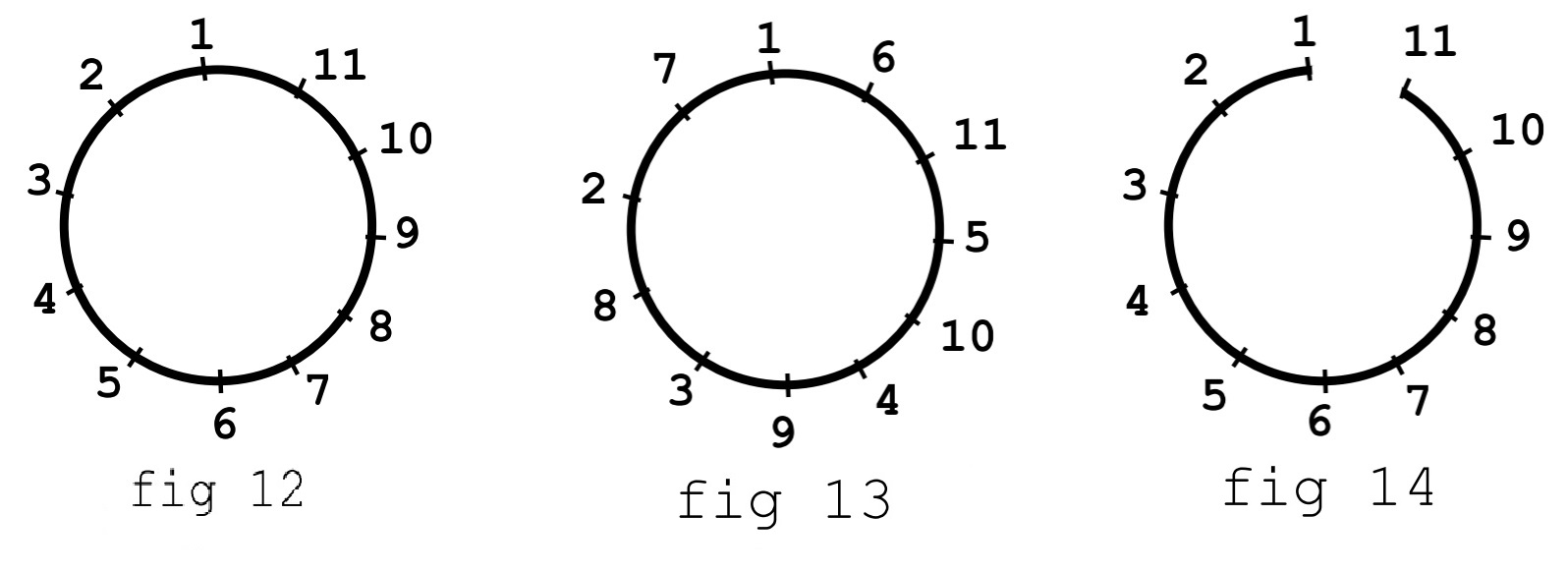 In questa situazione, poiché i primi elementi sarebbero collegati agli ultimi, è molto facile che in un certo elemento di struttura ci siano nodi etichettati con numeri molto diversi tra loro (figura 12). Tale problema può essere mitigato con una numerazione alternativa (figura 13) o con programmi che, empiricamente, cercano di individuare automaticamente la numerazione migliore.
In questa situazione, poiché i primi elementi sarebbero collegati agli ultimi, è molto facile che in un certo elemento di struttura ci siano nodi etichettati con numeri molto diversi tra loro (figura 12). Tale problema può essere mitigato con una numerazione alternativa (figura 13) o con programmi che, empiricamente, cercano di individuare automaticamente la numerazione migliore.
Si può notare che la figura 14 differisce dalla 12 solo per la mancata chiusura dell'anello: venendo meno il contatto tra i nodi 1 e 11, in questa struttura la banda risulta essere la migliore possibile, mentre nella figura 12 era la peggiore, pur avendo la stessa numerazione dei nodi.
Poiché tuttavia, nel peggiore dei casi, non si è comunque occupata più memoria di quanta ne occupa la matrice piena, la trasformazione di K in matrice bandata è un metodo comunque vantaggioso, o al più ininfluente, ma sicuramente non peggiorativo (come invece rischiava di essere la memorizzazione in forma sparsa).
Se il problema è lineare, la larghezza di banda resta sicuramente costante anche al procedere dei calcoli, poiché in quel caso K stessa è costante. In altri casi si può invece avere una variazione, come si vede da questo esempio:
Se si vuole ora modellare il contatto monolatero tra i due lati opposti della struttura bisogna imporre al programma di calcolo il vincolo di contatto, che impedisce la compenetrazione delle parti quando esse si avvicinano troppo. Una volta che il contatto avviene, quindi, ci sarà l'imposizione che $u_{\perp i}=u_{\perp j}$, oppure che sia presente una molla di rigidezza infinita tra i due punti venuti in contatto… in ogni caso, si è creata una connessione tra due elementi lontani tra loro, quindi è facile che ora ci sia un ponte elastico tra gradi di libertà dai valori molto diversi, causando un aumento della larghezza di banda.
 Un altro caso che eventualmente può presentarsi è quello di frattura del materiale: in questo caso la larghezza di banda si riduce.
Un altro caso che eventualmente può presentarsi è quello di frattura del materiale: in questo caso la larghezza di banda si riduce.
Adattamento del codice alla matrice in forma bandata
La trasformazione della matrice di rigidezza della struttura in matrice bandata comporta anche la necessità di modificare il programma deputato al calcolo della soluzione: in particolare si dovranno apportare delle modifiche alle subroutine di vincolamento e assemblaggio, nonché al solutore.
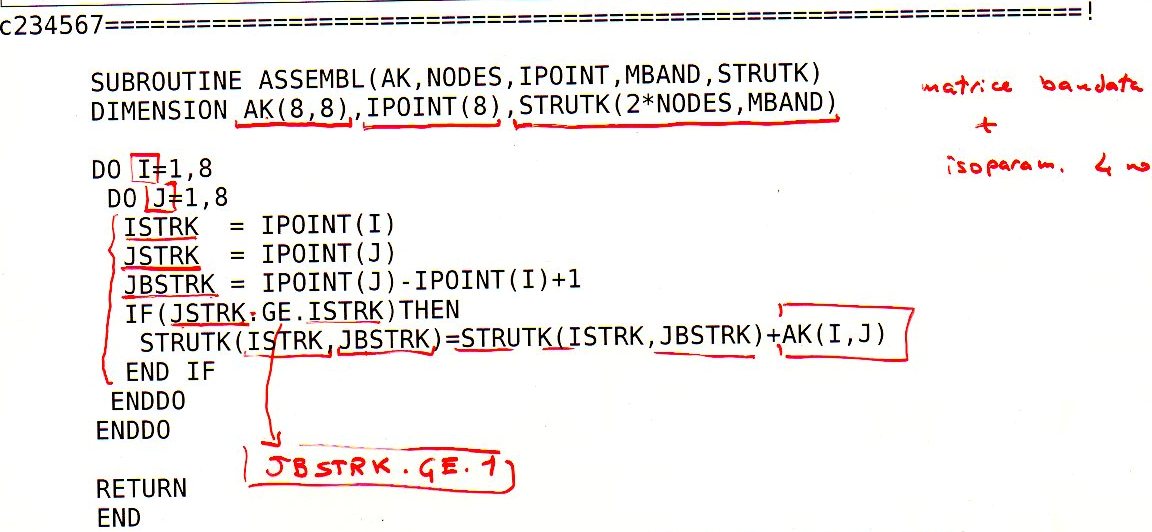
Questa è la subroutine di assemblaggio: in ingresso ha le variabili AK (la matrice di rigidezza $K_{el}$ di un generico elemento, di ordine 8), IPOINT (un vettore di 8 elementi, che rappresenta i gradi di libertà globali associati a quelli locali dell'elemento), STRUTK (matrice K di struttura, con numero di righe pari ai gradi di libertà, ovvero il doppio del numero di nodi NODES, e numero di colonne pari alla larghezza di banda MBAND). Il programma scorre sugli elementi di $K_{el}$, con due cicli nidificati (i è l'indice delle righe e j delle colonne). ISTRK e JSTRK sono gli indici i e j della matrice K di struttura (letti nel vettore IPOINT), cioé la posizione in cui si dovrà collocare il contributo associato a un dato elemento di $K_{el}$. Infine, JBSTRK è la colonna j della matrice bandata: non si indica la riga perché coincide con quella di K di partenza. Vale la relazione JBSTRK=IPOINT(J)-IPOINT(I)+1 poiché (considerando una qualsiasi riga) il numero di colonna della matrice bandata è uguale al numero di colonna della matrice di partenza, a cui bisogna sottrarre il numero di elementi sottodiagonali che si trovano sulla stessa riga (ovvero IPOINT(I)-1). Non si ha la certezza che un elemento che si trova nella parte sopradiagonale di $K_{el}$ risulti nella parte sopradiagonale anche di K, una volta assemblato: per questa ragione, è necessario che il codice legga tutti gli elementi di $K_{el}$, anche quelli sottodiagonali, poi un ciclo if discrimina il caso il cui un elemento di $K_{el}$ finisca nella parte sopradiagonale di K (nel qual caso verrà assemblato) da quello in cui finisce nella parte sottodiagonale (nel qual caso non viene considerato, in quanto verrà assemblato l'elemento di posto simmetrico e uguale valore, che finirà sopra alla diagonale in K). Questo ciclo if è fondamentale: senza di esso si avrebbero problemi di segmentation fault, perché si scriverebbero numeri in celle non allocate in memoria.
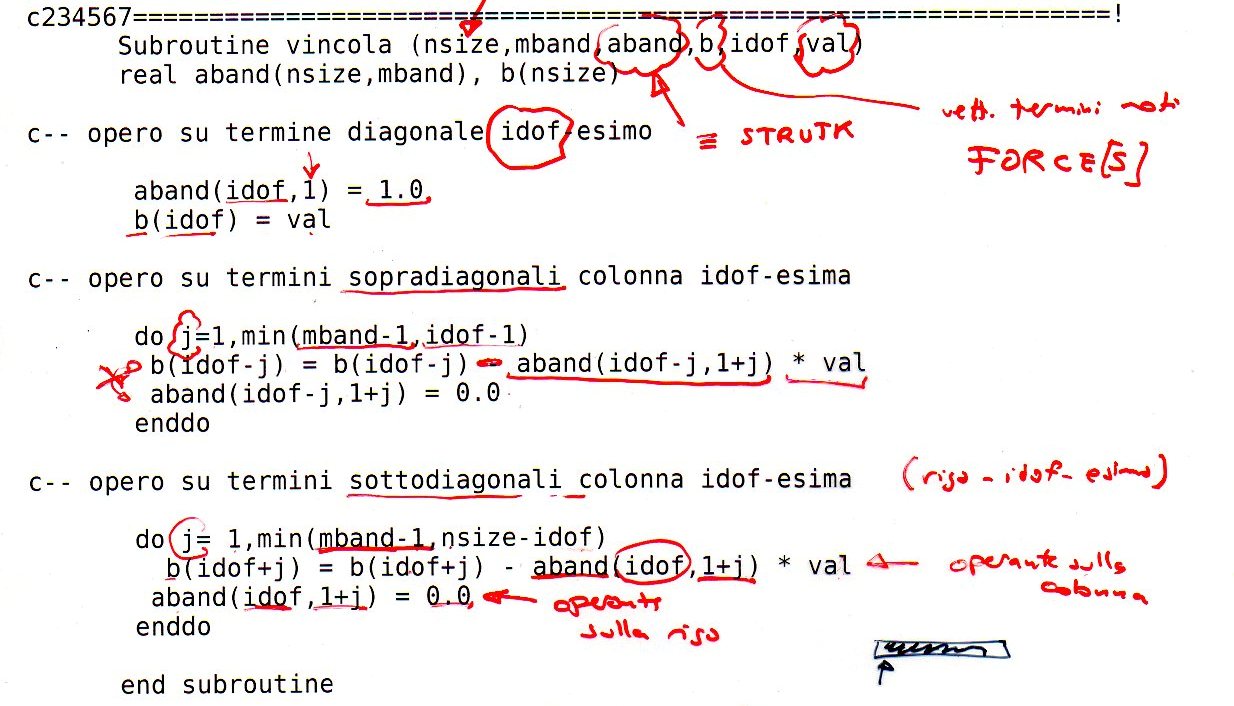
Questa è la subroutine di vincolamento, che impone i valori ai vari gradi di libertà. In ingresso si trovano NSIZE (il numero di gradi di libertà, pari al doppio del numero di nodi NODES), MBAND (la larghezza di banda), ABAND (la matrice K in forma bandata), b (il vettore dei termini noti), idof (lo specifico grado di libertà da vincolare) e val (il valore imposto a quel grado di libertà). La scrittura aband(idof,1)=1.0 rende uguali a 1 il termine diagonale di K (preso dalla prima colonna della matrice bandata aband) associato al grado di libertà da vincolare. b(idof)=val impone il valore desiderato al grado di libertà idof-esimo. Ora si devono azzerare i termini della riga (e anche colonna) idof-esima non diagonali, ma prima di farlo è necessario spostare il loro contenuto a termine noto, moltiplicandolo per lo specifico valore val e cambiandolo ovviamente di segno. Per questa operazione, si deve guardare la colonna idof-esima di K: i termini sopradiagonali di quella colonna si trovano nelle corrispondenti righe della matrice bandata aband (con l'elemento sulla diagonale nella colonna 1, quello subito sopra in colonna 2 ecc.), mentre quelli sottodiagonali non vengono riportati, perchè sono i simmetrici di altri elementi sopra alla diagonale (e in colonne diverse, pertanto vengono assemblati in un altro momento). La situazione appare dunque così: