cdm.ing.unimore.it

I problemi di contatto possono essere suddivisi in due tipologie, problemi diretti e problemi inversi:

- nei problemi diretti, noto il carico P, si deve trovare lo schiacciamento $\delta$;

- nei problemi inversi, noto lo schiacciamento, si deve trovare la distribuzione di pressione $p$. In genere il problema inverso risulta decisamente più complesso.

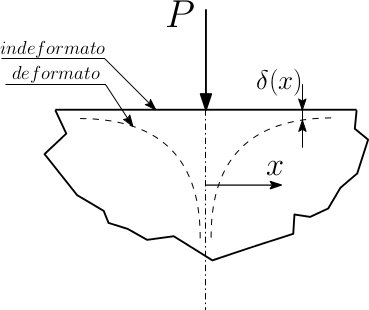
Si porta come esempio il caso di un indentatore rettangolare rigido a spigoli vivi premuto contro un semipiano elastico deformabile.

È stata trovata la formulazione matematica esatta della distribuzione di pressione di contatto $p(x)$ dovuta all'abbassamento uniforme del tratto caricato:

$p(x)=\frac{1}{\sqrt{1-x^2}}$ per $-1<x<1$

Si può notare che la funzione è simmetrica, infinita ai bordi e finita al centro. Il fatto che la pressione tenda a $\infty$ è giustificato dall'andamento della deformata in corrispondenza degli spigoli: tutte le volte che la deformata presenta un gradino, in quel punto esiste un picco di pressione matematicamente infinito.

Per quanto riguarda il problema di contatto diretto la pressione viene modellata come l'unione di infinite forze concentrate infinitesime adiacenti. Il problema può essere perciò ridotto allo studio dell'effetto una singola forza concentrata $P$ e poi ricomposto attraverso lo svolgimento di un integrale. Si considera quindi un carico concentrato $P$ agente sul semipiano deformabile.

Ci si aspetta che l'abbassamento del semipiano nel punto di applicazione della forza sia infinito. Infatti il carico concentrato, finito, agisce su un'area infinitesima (come la lama di un coltello spaventosamente affilata). La funzione che meglio descrive l'abbassamento è di tipo logaritmico, ed è detta soluzione di Boussinesq:

$\delta(x)=\alpha\frac{P}{E}log|x|+c$

Il coefficiente $\alpha$ è stato introdotto per considerare un termine funzione di tensione/deformazione piana e del coeff. di Poisson. In particolare

La funzione è formalmente esatta, ma presenta una forte imprecisione: mentre è accettabile che $\delta(0) = ∞$, non lo è che $\delta(∞) = ∞$, ossia che $\delta(x)=\infty$ quando ci si trova lontano del carico $P$. Nonostante questa soluzione sia parzialmente errata, al giorno d'oggi è la più accurata per lo studio di questo problema. La costante $c$ è presente a causa dei moti di spostamento di corpo rigido.

Quando è presente un solo carico concentrato è naturale posizionare l'asse $x$ a partire dal punto di applicazione della forza e definire $\delta$ come $\delta(x)$. Il problema sorge quando ho più di un carico.

Se si hanno due carichi $P_{1}$ e $P_{2}$, non basta più una variabile $x$ per definire l'abbassamento, ma ne servono due: la variabile $x$ definirà la posizione dei carichi $P_{1}$ e $P_{2}$ rispetto ad un punto arbitrario, mentre la variabile $y$ indicherà la posizione in cui calcolare l'abbassamento. Utilizzando solamente la variabile $x$, si troverebbe sempre lo spostamento sotto il carico in questione, mentre si cerca lo spostamento in un punto qualsiasi.

$\delta(y)=\frac{P_{1}}{E}log|x_{1}-y| + \frac{P_{2}}{E}log|x_{2}-y|$

L'effetto del carico distribuito può essere visto come una generalizzazione degli effetti dei singoli carichi concentrati. La relazione tra abbassamento e carico distribuito si ottiene tramite integrazione sul dominio della relazione precedente:

$\delta(y)=\frac{1}{E}\int_{x_1}^{x_2}\,p(x)\,log|x-y|\,dx$

Tale equazione presenta una variabile esterna $y$ e una variabile interna $x$, detta dummy variable. L'integrale è la sommatoria dell'influenza dei vari carichi concentrati $p(x)dx$ nella variabile $x$ che determinano l'abbassamento in $y$.

: da correggere e integrare, non richiesto in sede d'esame A.A. 2015/2016

Si considera ora il problema inverso: l'abbassamento è noto e la distribuzione di pressione è incognita. La scrittura classica del problema si ottiene derivando l'equazione dell'abbassamento rispetto alla variabile esterna $y$ e ponendola uguale a $0$. L'abbassamento deve infatti essere costante in quanto la parte indentata rimane piatta:

$\frac{d\delta(y)}{dy}=\frac{1}{E}\int_{x_1}^{x_2}\,\frac{p(x)}{y-x}\,dx = 0$

Questa è la forma standard dell'equazione integrale dei problemi di contatto, nella variabile di integrazione $x$ e nella variabile esterna $y$. Gli integrali del tipo $\int_{x_1}^{x_2}\,\frac{p(x)}{y-x}\,dx$ sono detti integrali di Chebyshev o di Cauchy. Bisogna trovare la pressione di contatto $p(x)$ che annulla l'integrale. Nel caso in esame dell'indentatore rettangolare l'integrale di Cauchy assume la forma:

$\frac{1}{E}\int_{-1}^{1}\,\frac{1}{(y-x)(\sqrt{1-x^2})}\,dx = 0$ $\quad$ per ogni $y$ tale che $-1<y<1$

… non torna…

Si nota che quando $x$ si avvicina a $y$ da sinistra il denominatore tende a $0$ e la funzione tende a $+∞$, o a $-∞$ se da destra. Siccome il denominatore passa per zero, la funzione nel suo complesso ha una discontinuità saltando da $+∞$ a $-∞$. Si riesce a dimostrare che all’interno del dominio le due punte che vanno a $∞$ si compensano e l'integrale non è più divergente. Al contrario, se si include nel dominio anche la frontiera il picco della funzione non viene compensato e l'integrale diverge. Si è trovato quindi un integrale piuttosto insolito, che risulta finito se si escludono gli estremi di integrazione e che invece diverge se si includono, mentre solitamente nel calcolo di un integrale è ininfluente includerli o meno.

DA CORREGGERE E INTEGRARE NELLA PARTE DELLA SOLUZIONE DELL'INDENTATORE!!!! (NdEB.)

Si cercherà di trovare l'andamento delle deformate di un albero a gomiti vincolato tramite tre differenti tipologie di vincoli simmetrici. L'albero a gomiti può essere visto come un portale composto da due tratti rettilinei laterali (albero), due tratti verticali (maschette) e una traversa (perno di manovella) caricata al centro da un carico $P$. Le varie tipologie di vincoli cercano di modellizzare gli effetti dei cuscinetti sull'albero. Questa semplificazione è piuttosto accurata per le due campate estremali di un albero a gomiti, ed è molto meno adatta per quelle centrali, che hanno scarse possibilità di deformarsi lateralmente.

- Caso 1:

L'albero è appoggiato su due carrelli. E' presente una labilità laterale in quanto i carrelli posso scorrere, ma dato che la struttura è simmetrica con caricamento simmetrico tale labilità può essere trascurata. Per essere realistico il vincolo dovrebbe essere composto da un carrello e da una cerniera, ma in questo modo si perderebbe la simmetria del problema. La curvatura della struttura segue l'andamento del momento flettente, dunque nel tratto centrale $CD$ $Mf$ non è costante, nel tratto $BC$ $Mf$ è costante in quanto il braccio della forza P è costante (deformata ad arco di cerchio), e nel tratto $AB$ $Mf$ è ancora non costante. Applicando le regole della conservazione della curvatura e dell'angolo retto si ottiene la seguente deformata:

- Caso 2:

In questo caso i vincoli sono 2 cerniere che forniscono una reazione orizzontale e una verticale. Nel tratto verticale $BC$ $Mf$ non è costante in quanto la reazione orizzontale ha braccio non costante, la deformata risulta quindi a forma di S e presenta un flesso. Se la reazione orizzontale fosse assente, la curvatura nel tratto verticale BC sarebbe costante come nel primo caso. Per rispettare le regole di conservazione della curvatura e dell'angolo retto è necessario posizionare un flesso anche nel tratto CD, ottenendo la seguente deformata:

- Caso 3:

In questo caso i 2 vincoli impediscono la rotazione e la traslazione verticale delle estremità dell'albero,ma non ne precludono la traslazione orizzontale. Dato che il vincolo mette in gioco, in aggiunta ad una reazione verticale, anche una coppia, il tratto $CB$ è caricato da quest'ultima e da una forza con braccio costante: la curvatura rimane costante, dunque deforma ad arco di cerchio. La parte estremale del tratto AB, invece, non potendo né traslare verticalmente né ruotare, deve rimanere rettilinea. Dovendo rispettare le regole di continuità della curvatura e dell'angolo retto è necessario posizionare un flesso nella parte di AB prossima alla maschetta, parte che non rimane rettilinea. Si ottiene dunque la seguente deformata:

.