Indice
Link di forza/ Momenti risultanti distribuiti RBE2-RBE3
Forze concentrate su elementi discretizzati
Trave:
mi aspetto un “delta” finito perchè la forza F è spalmata su un'area finita, infittendo la mesh.
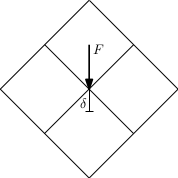
Piastre alla Kirkhhoff:
Se applico carico F perpendicolare al piano ho spostamento “delta” finito perchè la singolarità è una tensione tagliante e non da deformazioni.
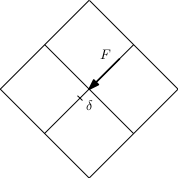
Se F è entropiano non posso applicare carchi concentrati, “delta” non limitato —> ho componenti di deformazione (comportamento membranale). Nella teoria dei continui elastici F è spalmato su un'area. Allora posso applicare carichi concentrati solo su elementi trave!!
Devo “inventare” metodi che consentano di risolvere strutture con carichi applicati senza introdurre singolarità. La zona di interesse dello stato di carico non è in prossimità di quest'ultima ma in prossimità del vincolo.
Come nel disegno qui sopra, se la F non è applicata nel centro di taglio, avrei anche la presenza di momento torcente che genera “Tau”, perciò non è conveniente. Allora uso dei link cinematici per spalmare le forze concentrate: i più utilizzati sono gli RBE2 e gli RBE3. Gli RBE sono link, ovvero delle connessioni tra nodi della struttura in esame a nodi particolari, che godono di particolari proprietà.Gli schemi RBE vengono utilizzati per affrontare lo studio di una struttura connessa ad un’altra senza dover completamente affrontare un’analisi FEM della seconda.
RBE2 Nastran
Vincolo di moto di corpo rigido: prendo una sezione, prendo tutti i nodi appartenenti alla sezione, prendo un nodo di controllo esterno alla sezione a cui andrò ad applicare il carico.
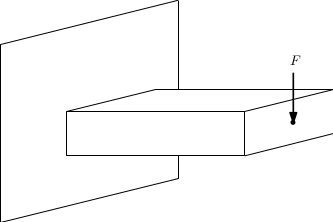
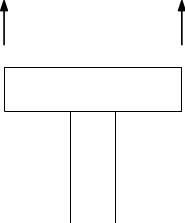
Tutti i nodi devono muoversi con vincolo di corpo rigido rispetto al nodo di controllo. Tutti i nodi della sezione sono dipendendi tranne quello di controllo (di maniglia) che è indipendente. Però la sezione non può più ingobbarsi, infatti il problema è dovuto ad un irrigidimento locale della struttura. Se ho una struttura di questo tipo e voglio applicare due forze ho due possibilità:
Caso 1: la struttura può essere vista come l'unione di due corpi rigidi studiabili nel caso in esame.
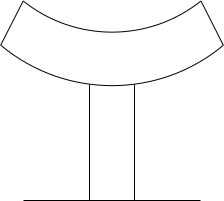
La deformazione avviene come illustrato in figura a seguito dell'applicazione delle due forze concentrate.
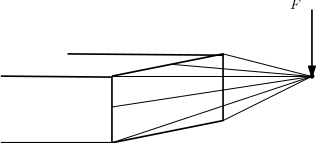
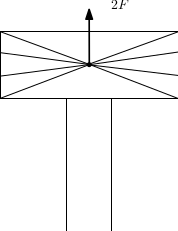
Caso 2: in questo caso la struttura è caricata da un'unica forza in mezzeria pari a 2F e si utilizza un solo corpo rigido che sintetizza l'intera struttura.
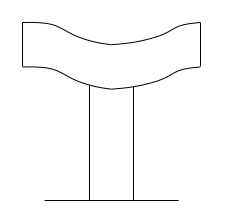
Nel caso deformato le facce devono restare parallele tra loro. In conclusione l'RBE2 non si utilizza in maniera estesa alla struttura ma viene applicato solo localmente a causa dell'irrigidimento della struttura (esempio banco prova telaio).
RBE3 Nastran
Gli RBE3 sono link di carico/coppia distribuita o link di rotazione/spostamenti medi. Non irrigidiscono la struttura e vengono utilizzati nei collegamenti punto-punto.
“Pi” sono i nodi e ad ogni punto viene associao un proprio peso “qi” mentre il sistema di riferimento deve essere principale d'inerzia. I pesi sono legati alle aree nodali: i nodi su mesh più grezze hanno pesi maggiori rispetto a zone con mesh più fini.
Si considera un nodo dipendete C di coordinate xC,yC, yC ,zC detto nodo di controllo ed una nuvola di n nodi indipendenti Pi di coordinate xi,yi,zi e con peso relativo qi. Si considera applicato al nodo C un sistema di azioni esterne nella forma delle tre componenti di forza UC,VCWC e nelle tre componenti di momento ΩCΦCΨC. Mentre U, V, W, sono le forze dei Pi e u,v,w, sono le rispettive coordinate degli spostamenti. Prendo il nodo C e applico forze e/o coppie sui nodi tenendo in considerazione i rispettivi pesi (applico più carico in presenza di nodi elastici con peso maggiore).
Si definisce un centro di massa G della nuvola di punti, le cui coordinate (riprendendo le formulazioni classiche della meccanica razionale)sono
$ x_{G}= \frac{\Sigma_{i}q{i}x{i}}{\Sigma_{i}q{i}}$,$ y_{G}= \frac{\Sigma_{i}q{i}y{i}}{\Sigma_{i}q{i}}$,$ z_{G}= \frac{\Sigma_{i}q{i}z{i}}{\Sigma_{i}q{i}}$
Si suppone inoltre che il sistema di riferimento Gxyz sia principale d'inerzia per la distribuzione di pesi. Nel caso tale ipotesi non sia verificata occorre procedere come segue:
- cambio di sistema di riferimento da terna xyz ad una terna ausiliaria “epsilon eta zetamaiuscolo”con orientazione principale d'inerzia per la specifica distrubuzione RBE3.
- applicazione della procedura sotto descritta utilizzando posizioni nodali e componenti di forza/momento scomposte secondo la terna ausiliaria “epsilon eta zetamaiuscolo” in luogo della predefinita xyz.
- trasformazione inversa delle quantità risultanti da terna ausiliaria “epsilon eta zetamaiuscolo” a terna originale xyz.
Si definisce quindi una prima relazione di dipendenza cinematica, per cui le rototraslazioni
$\underline{\delta}_{C}= [u_{C} v_{C} w_{C} \theta_{C} \phi_{C} \psi_{C}]^T$
di C sui tre assi $x$, $y$,$z$ sono definite in funzione delle rototraslazioni
$\underline{\delta}_{G}= [u_{G} v_{G} w_{G} \theta_{G} \phi_{G} \psi_{G}]^T$
del centro di massa $G$ secondo il vincolo di rototraslazione rigida
$$ \begin{bmatrix} u_{C}\\ v_{C}\\ w_{C}\\ \theta_{C}\\ \phi_{C}\\ \psi_{C} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & +(z_{C}-z{G}) & -(y_{C}-y{G}) \\ 0 & 1 & 0 & -(z_{C}-z{G}) & 0 & +(x_{C}-x{G}) \\ 0 & 0 & 1 & +(y_{C}-y{G}) & -(x_{C}-x{G}) & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u_{G}\\ v_{G}\\ w_{G}\\ \theta_{G}\\ \phi_{G}\\ \psi_{G} \end{bmatrix} $$
La matrice sopra riportata prende il nome di “Lcg” e sotto l'ipotesi di piccole rotazioni ha una dipendenza lineare.
In questo modo si arriva ad una relazione “triangolare” dove la relazione tra il punto di controllo e i nodi indipendenti $P_{i}$ è mediata dal baricentro che funge da tramite.
Nello schema seguente si illustra la distribuzione dei momenti rispetto al sistema cartesiano e approciando i momenti nella forma “forza per braccio” più congeniale alla trattazione.
Per quanto riguarda le relazioni relative:
All'imposizione di tali relazioni cinematiche è associata una riduzione a nuovo punto di applicazione G delle azioni agenti su $C$, con l'introduzione di opportuni momenti di trasporto (vedi Teorema di Huygens) come da
$\underline{F}_{G}=[\underline{\underline{L}}_{CG}]^{T} \cdot \underline{F}_{C} $, $\underline{F}_{G}=[U_{G} V_{G} W_{G} \Theta_{G} \Phi_{G} \Psi_{G}]^T$
Si definisce quindi una seconda relazione di dipendenza per cui da una parte lo spostamento del nodo $G$ risulti la media pesata degli spostamenti ai nodi $P_{i}$, ovvero $ u_{G}= \frac{\Sigma_{i}q{i}u_{i}}{\Sigma_{i}q_{i}}$,$ v_{G}= \frac{\Sigma_{i}q_{i}v_{i}}{\Sigma_{i}q_{i}}$,$ w_{G}= \frac{\Sigma_{i}q_{i}w_{i}}{\Sigma_{i}q_{i}}$,
e dall'altra le forze applicate in $C$ e ridotte a $G$ si distribuiscano ai nodi $P_{i}$ secondo i pesi dati, ossia $ U'_{i}=U_{C} \frac{q_{i}}{\Sigma_{i}q_{i}}$,$ V'_{i}= V_{C}\frac{q_{i}}{\Sigma_{i}q{i}}$,$ W'_{i}= W_{C}\frac{q_{i}}{\Sigma_{i}q_{i}}$,
Per quanto riguarda la distribuzione dei momenti ridotti a $G$ sui nodi $P_{i}$, si preferisce operare in termini di una seconda quota di forze nodali $U''_{i}$,$V''_{i}$,$W''_{i}$ piuttosto che in termini di una quota di momenti ${\Theta}'_{i}$,${\Phi}'_{i}$,${\Psi}'_{i}$. Riferendosi alla figura precedente si considerano le componenti di momento $\Theta_{G}$,$\Phi_{G}$,$\Psi_{G}$ singolarmente nella riduzione a sistemi di forze equivalenti.
Dispensa prog. assistita aggiornata a data odierna
D'OH: la trattazione cinematica che lega le rototraslazioni del baricentro agli spostamenti dei nodi $P_i$ basata sul prodotto scalare pesato
$\langle \cdot , \cdot \rangle_q$
come svolta alla lavagna a fine lezione non risulta corretta per le rotazioni come evidenziato da un vostro collega. Riferirsi alla dispensa sopracitata o alla pagina wiki dell'anno scorso, paragrafo “Approfondimento: analisi cinematica RBE3”. Sorry.