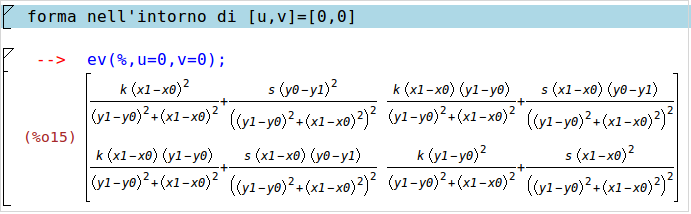TEMP TEMP
TEMP
TEMP
TEMP
TEMP
Instabilità delle strutture elastiche
Parliamo di problemi di instabilità in strutture elastiche.
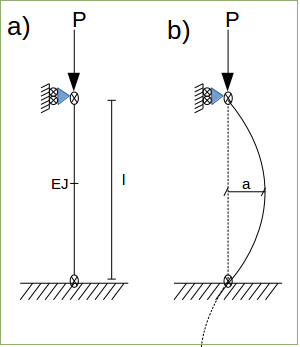
Durante il corso della triennale è stato già visto il problema di instabilità della trave a compressione, tipicamente una trave flessionale, vincolata con una cerniera e un carrello, di lunghezzale sezione caratterizzata dal modulo elastico a flessione $EJ$, si dovrebbe sapere che se caricata da un carico complessivo $P$, se:
- $ P < P_{cr} $ allora la soluzione è in sola compressione della trave, ed è la soluzione che si ottiene facendo l'equilibrio sull'indeformata;
- $ P > P_{cr} $ allora la soluzione compressiva è una delle possibili, ma si affiancano anche delle soluzioni flessionali. Queste soluzioni non si trovano facendo l'equilibrio sull'indeformata ma si dovranno impostare delle equazioni di equilibrio sulla deformata. La deformata avrà una forma sinusoidale, e la sua ampiezza $a$ è arbitraria.
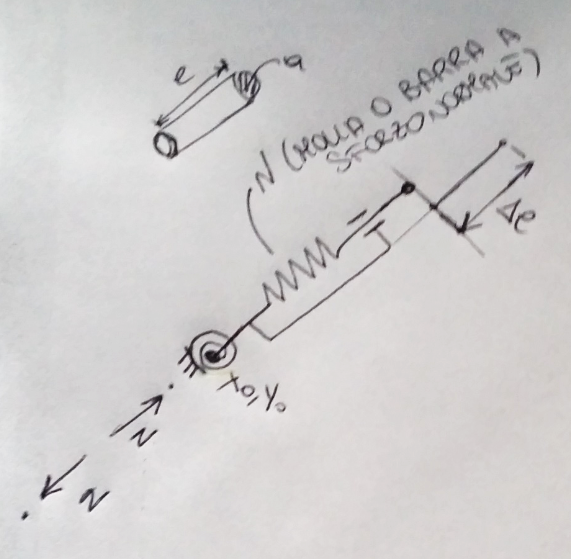
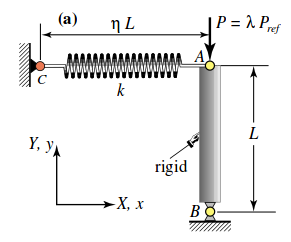
Dove: $ P_{cr}=(π^2 EJ)/l^2 $ . Affrontando il problema dal punto di vista analitico, si arriverà ad un equazione differenziale del secondo ordine, si cercheranno le soluzioni non banali, ecc.. Questo approccio è possibile solo se la struttura è particolarmente semplice, se già si prova a complicare la struttura, la complessità diventa non più maneggiabile. Ci concentriamo su problemi di instabilità di strutture discretizzate, quindi composta da elementi finiti. Per rendere più semplice l'approccio al calcolatore (maxima) il prof. ha inventato un elemento abbastanza semplice che attraverso maxima può essere esplorato. Ovvero, un elemento barra, incernierata a telaio (2 nodi), con due elementi elastici:
- rigidezza assiale, barra assialmente comprimibile o molla;
- molla torsionale connessa alla barra (ad un capo) e a telaio (altro capo);
 in più guido la parte terminale della barra con un corsoio che lo collega al gambo attaccato alla cerniera.
in più guido la parte terminale della barra con un corsoio che lo collega al gambo attaccato alla cerniera.
In pratica è una molla incernierata con possibilità di imporre una reazione elastico-torsionale alla base.
La rigidezza della molla la chiamiamo $k$, mentre quella della molla torsionale $s$ .
Perchè la scelta di questo elemento?
Perchè ha due g.d.l $u$ e $v$ e solo quelli, perché l'altro nodo è implicitamente collegato al telaio. Elemento finito un po' particolare perché la matrice rigidezza non nasce singolare, perché uno dei due nodi è collegato a telaio, ma è una 2×2!
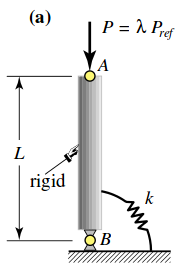
Consideriamo una $k→∞$, perdendo la parte della deformabilità del nostro elemento, per rendere più semplice la trattazioni in termini di equilibrio e analizziamo il problema: è un elemento ad asse verticale, con supporto torsionale alla base, di rigidezza $s$ , estensione $a$ e caricata da un carico $P$ , la struttura in questo caso avrà un solo g.d.l. ovvero la rotazione θ, l'asta può solo ruotare.
Quali sono le condizioni di equilibrio di questa struttura?
Allora se facciamo un equilibrio sulla indeformata, e ciò è semplice perché l'asta rimane verticale e lavora in compressione con sforno normale $P$, e questa è l'unica soluzione.
Supponiamo adesso di fare l'equilibrio sulla deformata …si sta supponendo che la direzione del carico $P$ sia costante nello spazio, ovvero la retroazione di $P$ non segua l'inclinazione della barra; questo è necessario per avere un campo di forze conservativo, questo richiede proprio che le forze abbiamo direzione fissa nello spazio e non fissa rispetto al punto di applicazione sulla struttura. Se la forza avesse una direzione solidale al punto di applicazione sulla struttura questa forza si riorienterebbe con l'asse della trave… .
Se il campo di forze è conservativo ammette un potenziale, quindi se il campo di forze ammette un potenziale, l'energia totale della struttura ha due contributi, il potenziale delle forze e l'energia potenziale elastica degli elementi deformabili.
Calcoliamo l'equazione di equilibrio alla rotazione dell'asta rispetto alla cerniera in O. Allora, abbiamo la molla a torsione che reagisce con una coppia di entità -sθ, agente in direzione oraria quindi la consideriamo negativa, in più abbiamo una reazione indotta dalla forza $P$ per il braccio $a⋅sin(θ)$ che è antioraria, e il tutto dovrà essere uguale a 0, avremo dunque:
$$ -s⋅θ+P⋅a⋅sin(θ)=0 $$
L'equazione di equilibrio ci dice che le soluzioni del problema sono 2:
- $ θ=0∀P$: questo da equilibrio (0=0)
- $ θ≠0→ P=(s⋅θ)/(a⋅sin(θ))$: e anche qui ho equilibrio.
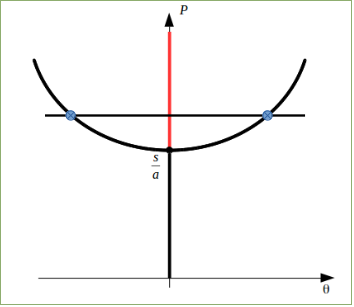
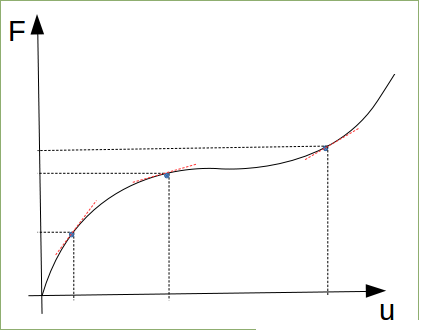
La quantità $θ/(sin(θ))$ tende a $1$ per $θ→0$ e in generale $θ/(sin(θ))≥1$ , quindi diciamo che questo carico è funzione di $θ$ quindi per $θ≈0→ P=s/a=[(N⋅mm)/rad]⋅[1/mm]$ semplificando rimangono [N] quindi P è oggettivamente una forza. Questo carico P ovviamente al variare di θ cresce. Possiamo plottare il tutto con maxima:
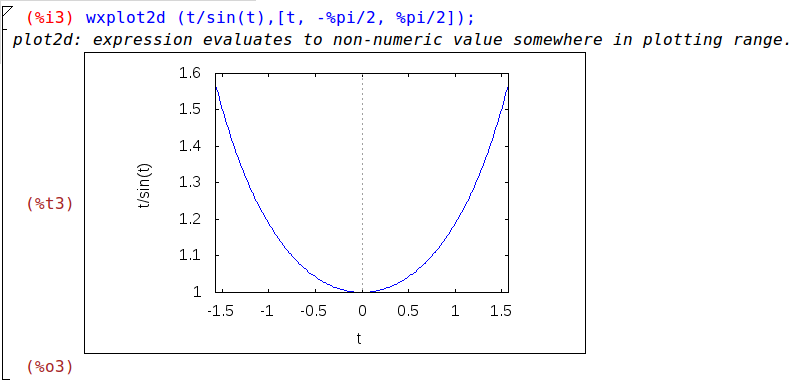 Come si può vedere è una funzione crescente, quindi risulta che P non può essere minore di una quantità pari a s/a, dunque θ≠0questa soluzione non è ammessa se P<s/a, viceversa è ammessa se maggiore o uguale.
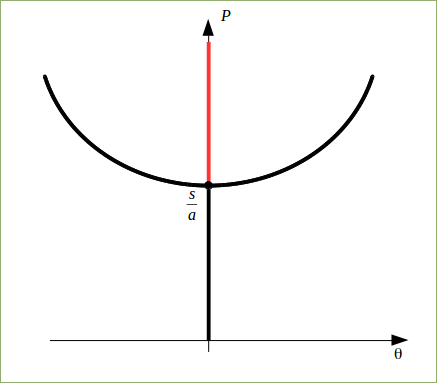
Si possono plottare le condizioni di equilibrio su un diagramma, in cui avremo Pin ordinata e θin ascissa, e individuo il valore di s/asu P, e considero le condizioni che possono essere di equilibrio. θ=0È di equilibrio fino a P=s/a, ma in realtà lo sarebbe ∀ P quindi anche sopra tale valore, poi ricopiando il grafico ottenuto in maxima, con vertice in [0;s/a] nell'intorno di tale punto ho 4 percorsi di possibile equilibrio.
Come si può vedere è una funzione crescente, quindi risulta che P non può essere minore di una quantità pari a s/a, dunque θ≠0questa soluzione non è ammessa se P<s/a, viceversa è ammessa se maggiore o uguale.
Si possono plottare le condizioni di equilibrio su un diagramma, in cui avremo Pin ordinata e θin ascissa, e individuo il valore di s/asu P, e considero le condizioni che possono essere di equilibrio. θ=0È di equilibrio fino a P=s/a, ma in realtà lo sarebbe ∀Pquindi anche sopra tale valore, poi ricopiando il grafico ottenuto in maxima, con vertice in [0;s/a]nell'intorno di tale punto ho 4 percorsi di possibile equilibrio.
Come si può vedere è una funzione crescente, quindi risulta che P non può essere minore di una quantità pari a s/a, dunque θ≠0questa soluzione non è ammessa se P<s/a, viceversa è ammessa se maggiore o uguale.
Si possono plottare le condizioni di equilibrio su un diagramma, in cui avremo Pin ordinata e θin ascissa, e individuo il valore di s/asu P, e considero le condizioni che possono essere di equilibrio. θ=0È di equilibrio fino a P=s/a, ma in realtà lo sarebbe ∀ P quindi anche sopra tale valore, poi ricopiando il grafico ottenuto in maxima, con vertice in [0;s/a] nell'intorno di tale punto ho 4 percorsi di possibile equilibrio.
Come si può vedere è una funzione crescente, quindi risulta che P non può essere minore di una quantità pari a s/a, dunque θ≠0questa soluzione non è ammessa se P<s/a, viceversa è ammessa se maggiore o uguale.
Si possono plottare le condizioni di equilibrio su un diagramma, in cui avremo Pin ordinata e θin ascissa, e individuo il valore di s/asu P, e considero le condizioni che possono essere di equilibrio. θ=0È di equilibrio fino a P=s/a, ma in realtà lo sarebbe ∀Pquindi anche sopra tale valore, poi ricopiando il grafico ottenuto in maxima, con vertice in [0;s/a]nell'intorno di tale punto ho 4 percorsi di possibile equilibrio.
 Lungo P, sopra il punto [0;s/a], il ramo me lo troverò in equilibrio instabile. Per vedere se la soluzione è instabile dovremo scrivere il potenziale.
Lungo P, sopra il punto [0;s/a], il ramo me lo troverò in equilibrio instabile. Per vedere se la soluzione è instabile dovremo scrivere il potenziale.
L'energia Potenziale U_tot contiene una quota parte derivante dall'elemento elastico, l'energia potenziale associata all'elemento elastico $1/2/sθ^2$ (s = rigidezza torsionale , θ= scostamento angolare) e devo aggiungere l'energia potenziale dei carichi, ora perché quel carico possiede un en.potenziale? Perché è un carico applicato a un punto, e lo posso considerare analogo ad una en. gravitazionale, e l'energia potenziale di questo tipo di forza è uguale ad una costante c, meno una quota parte ottenuta inserendo una rotazione θ che porta ad un abbassamento di P di un valore pari a a(1-cos(θ)), quindi l'energia totale sarà:
$U_tot=1/2⋅s⋅θ^2+c-P⋅a⋅(1-cos(θ))$
Quando il punto si abbassa di quella quantità, il lavoro compiuto da quella forza andrà quindi sottratto all'energia potenziale.
Mi accorgo a questo punto di due cose, se avessi lavorato con piccole rotazioni 1-cos(θ)sarebbe stato implicitamente nullo, e quindi non avremmo avuto questo contributo -P⋅a⋅(1-cos(θ)). Da qui la necessità di lavorare sempre con grandi rotazioni, e non sviluppare al primo ordine le funzioni trigonometriche. Calcolato U_tot devo fare la derivata seconda, ed avremo equilibrio se la derivata seconda è positiva, è un minimo dell'energia potenziale, se la derivata seconda è negativa è un massimo dell'energia potenziale.
 Quando vado a valutare la condizione della derivata seconda dell'energia potenziale per $t=0$, trovo che gli equilibri per t=0 sono stabili se l'oggetto $(s-a⋅P)$ è maggiore di 0 e instabili se minori di zero. Vedo inoltre che per $P=s/a$ avrò $s-(a⋅s)/a$ e quindi 0, dunque in condizioni di carico critico ho un equilibrio differente, mentre se P>P_criticodiventa dominante il secondo termine negativo e l'energia potenziale elastica è una funzione con derivata seconda negativa quindi quello che è un punto stazionario non è un minimo dell'energia potenziale elastica ma un massimo ed è quindi localmente instabile.
Quindi avremo che la zona in rosso è instabile, mentre quella in nero ha tutte soluzioni stabili.
I diagrammi di equilibrio si possono ricavare tramite l'energia potenziale elastica per derivazione, ovviamente l'equilibrio è un punto sezionale dell'energia potenziale elastica. L'energia potenziale elastica in più rispetto all'analisi dell'equilibrio dei corpi mi da anche la possibilità di calcolare la stabilità dell'equilibrio con la derivata seconda in maniera abbastanza semplice.
Il secondo percorso (quello curvo) è stabile, quindi il sistema non degenare da nessuna parte, anzi se prendo questa asta, questa sul percorso secondario, teoricamente sarebbe in grado di supportare carico infinito, perché se ottengo una rotazione abbastanza grossa, arrivo alla condizione in cui il carico sarà allineato all'oggetto, e questo sarà in grado di supportare quantità infinite di carico, sopratutto se non è deformabile. Quindi non è vero che è un fenomeno di instabilità, ma è un fenomeno di diversa stabilità. Dunque nell'intoro del punto [0,s/a]
per variazioni di P potrò muovermi lungo diversi percorsi di equilibrio.
Non è sempre così per sfortuna, perché quando c'è un problema di instabilità si assesta su una condizione secondaria, che, in questo caso, sarebbe molto più stabile della precedente.
Quando vado a valutare la condizione della derivata seconda dell'energia potenziale per $t=0$, trovo che gli equilibri per t=0 sono stabili se l'oggetto $(s-a⋅P)$ è maggiore di 0 e instabili se minori di zero. Vedo inoltre che per $P=s/a$ avrò $s-(a⋅s)/a$ e quindi 0, dunque in condizioni di carico critico ho un equilibrio differente, mentre se P>P_criticodiventa dominante il secondo termine negativo e l'energia potenziale elastica è una funzione con derivata seconda negativa quindi quello che è un punto stazionario non è un minimo dell'energia potenziale elastica ma un massimo ed è quindi localmente instabile.
Quindi avremo che la zona in rosso è instabile, mentre quella in nero ha tutte soluzioni stabili.
I diagrammi di equilibrio si possono ricavare tramite l'energia potenziale elastica per derivazione, ovviamente l'equilibrio è un punto sezionale dell'energia potenziale elastica. L'energia potenziale elastica in più rispetto all'analisi dell'equilibrio dei corpi mi da anche la possibilità di calcolare la stabilità dell'equilibrio con la derivata seconda in maniera abbastanza semplice.
Il secondo percorso (quello curvo) è stabile, quindi il sistema non degenare da nessuna parte, anzi se prendo questa asta, questa sul percorso secondario, teoricamente sarebbe in grado di supportare carico infinito, perché se ottengo una rotazione abbastanza grossa, arrivo alla condizione in cui il carico sarà allineato all'oggetto, e questo sarà in grado di supportare quantità infinite di carico, sopratutto se non è deformabile. Quindi non è vero che è un fenomeno di instabilità, ma è un fenomeno di diversa stabilità. Dunque nell'intoro del punto [0,s/a]
per variazioni di P potrò muovermi lungo diversi percorsi di equilibrio.
Non è sempre così per sfortuna, perché quando c'è un problema di instabilità si assesta su una condizione secondaria, che, in questo caso, sarebbe molto più stabile della precedente.
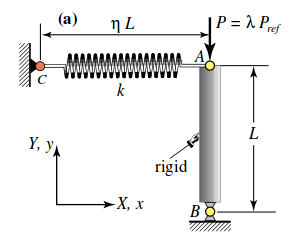
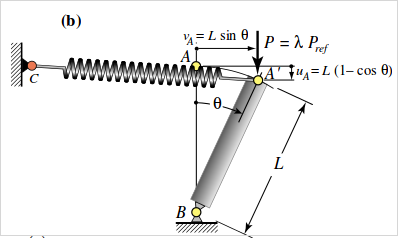 In realtà se utilizziamo un supporto diverso, per questa barra, invece di applicare una molla rotazionale in basso, applichiamo una molla stabilizzante, sopra. La molla stabilizzante mi definisce il posizionamento angolare della barra rigida, notiamo inoltre che per piccoli spostamenti, questa configurazione sarebbe del tutto equivalente alla molla torsionale. Perché sostanzialmente la molla per il braccio L mi darebbe una rigidezza torsionale e un posizionamento che entro la condizione iniziale è indistinguibile dalla molla torsionale di partenza.
Tuttavia in questo caso se vado a fare un'analisi dell'equilibrio in questa condizione, noto subito che è già più complicato perché il problema è asimmetrico, nel senso che una estensione con θnella direzione in figura, orienta la molla in maniera diversa (estensione con angolo negativo secondo la convenzione). Troveremo dei diagrammi (θ;P)che hanno localmente sulla soluzione secondaria un massimo per il carico. Diciamo che nel caso di molla torsionale avevamo una forma concava mentre qui avremo una forma convessa. Quindi se vado a fare l'analisi dell'energia potenziale alla derivata seconda vedo che questo ramo secondario a differenza del supporto con molla rotazionale alla cerniera dà un equilibrio stabile, ovvero se portiamo la struttura nella condizione della seconda figura, questa condizione può essere di equilibrio stabile, ma questo P è un valore di carico minore del P_transizionee in particolare, nessuno dei percorsi di equilibrio stabile è in grado di sopportare carico maggiore di questa P_transizione. Ricapitolando, l'equilibrio sul ramo secondario sarà ancora di tipo stabile, però, il carico applicato dovrà essere minore di quello di transizione, se mantengo un carico uguale a quello di transizione non sarò più in grado di equilibrarlo. Mentre sul ramo superiore ( sopra [0,s/a]) riesco a equilibrarlo sempre ma sarà un equilibrio instabile. Per cui questo sistema non riesce a sopportare in equilibrio stabile nessun livello di carico superiore a quello critico.
In realtà se utilizziamo un supporto diverso, per questa barra, invece di applicare una molla rotazionale in basso, applichiamo una molla stabilizzante, sopra. La molla stabilizzante mi definisce il posizionamento angolare della barra rigida, notiamo inoltre che per piccoli spostamenti, questa configurazione sarebbe del tutto equivalente alla molla torsionale. Perché sostanzialmente la molla per il braccio L mi darebbe una rigidezza torsionale e un posizionamento che entro la condizione iniziale è indistinguibile dalla molla torsionale di partenza.
Tuttavia in questo caso se vado a fare un'analisi dell'equilibrio in questa condizione, noto subito che è già più complicato perché il problema è asimmetrico, nel senso che una estensione con θnella direzione in figura, orienta la molla in maniera diversa (estensione con angolo negativo secondo la convenzione). Troveremo dei diagrammi (θ;P)che hanno localmente sulla soluzione secondaria un massimo per il carico. Diciamo che nel caso di molla torsionale avevamo una forma concava mentre qui avremo una forma convessa. Quindi se vado a fare l'analisi dell'energia potenziale alla derivata seconda vedo che questo ramo secondario a differenza del supporto con molla rotazionale alla cerniera dà un equilibrio stabile, ovvero se portiamo la struttura nella condizione della seconda figura, questa condizione può essere di equilibrio stabile, ma questo P è un valore di carico minore del P_transizionee in particolare, nessuno dei percorsi di equilibrio stabile è in grado di sopportare carico maggiore di questa P_transizione. Ricapitolando, l'equilibrio sul ramo secondario sarà ancora di tipo stabile, però, il carico applicato dovrà essere minore di quello di transizione, se mantengo un carico uguale a quello di transizione non sarò più in grado di equilibrarlo. Mentre sul ramo superiore ( sopra [0,s/a]) riesco a equilibrarlo sempre ma sarà un equilibrio instabile. Per cui questo sistema non riesce a sopportare in equilibrio stabile nessun livello di carico superiore a quello critico.
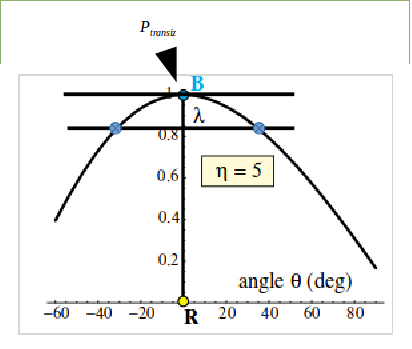 Quindi un sistema supportato come nel secondo caso, che per piccole rotazioni è del tutto analogo a quello con molla torsionale, non sarà in grado di supportare carichi maggiori di quello di transizione. Questo è un comportamento tipicamente instabile. Due comportamenti contrastanti, con un supporto alla base, ottengo un sistema che è in grado di supportare carichi anche maggiori di quello critico e se l'asta si allinea verso il basso potenzialmente infinito. Un diverso supporto, laterale, di quest'asta e il sistema non è in grado di supportare carichi maggiori di quello di transizione. Perché il carico di transizione viene chiamato critico? Perché parto da un sistema scarico, successivamente applico carichi via via crescenti e mi aspetto di avere una soluzione con risposta proporzionale al carico, questa quando si raggiunge il valore di transizione diventa non più unica e non più stabile, pertanto per quella soluzioni il carico di transizione è un carico critico. Ma non è sempre un carico critico per la struttura, il caso A non è critico ad esempio perché esiste una soluzione secondaria che non è più puramente compressiva ma è in rotazione, che è in grado di sopportare carichi potenzialmente fino a infinito, quando il sistema è allineato con la parte bassa. Quindi quando si parla di carico critico è quello relativo per la specifica soluzione che si sta seguendo da quando il sistema era scarico e via via si è aggiunto il carico, seguendo una soluzione, fino a quando questa non va in crisi, non va in crisi la struttura ma la soluzione.
Quindi un sistema supportato come nel secondo caso, che per piccole rotazioni è del tutto analogo a quello con molla torsionale, non sarà in grado di supportare carichi maggiori di quello di transizione. Questo è un comportamento tipicamente instabile. Due comportamenti contrastanti, con un supporto alla base, ottengo un sistema che è in grado di supportare carichi anche maggiori di quello critico e se l'asta si allinea verso il basso potenzialmente infinito. Un diverso supporto, laterale, di quest'asta e il sistema non è in grado di supportare carichi maggiori di quello di transizione. Perché il carico di transizione viene chiamato critico? Perché parto da un sistema scarico, successivamente applico carichi via via crescenti e mi aspetto di avere una soluzione con risposta proporzionale al carico, questa quando si raggiunge il valore di transizione diventa non più unica e non più stabile, pertanto per quella soluzioni il carico di transizione è un carico critico. Ma non è sempre un carico critico per la struttura, il caso A non è critico ad esempio perché esiste una soluzione secondaria che non è più puramente compressiva ma è in rotazione, che è in grado di sopportare carichi potenzialmente fino a infinito, quando il sistema è allineato con la parte bassa. Quindi quando si parla di carico critico è quello relativo per la specifica soluzione che si sta seguendo da quando il sistema era scarico e via via si è aggiunto il carico, seguendo una soluzione, fino a quando questa non va in crisi, non va in crisi la struttura ma la soluzione.
Andiamo a definire questi due problemi con l'elemento finito disegnato a inizio lezione. Definiamo la matrice rigidezza dell'elemento finito.
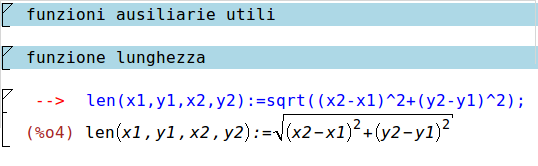
 Prima di tutto devo stare attento a gestire tutto in non linearità massiccia, cioè non si può supporre che nulla sia piccolo per cui utilizzo a piene mani funzioni trigonometriche non linearizzate e funzioni anche ad esempio distanza tra due nodi in forma non linearizzata. Di base cosa faccio,
definisco le funzioni ausiliarie, distanza tra due punti (x_1;y_1)e (x_2;y_2)come la radice della somma dei quadrati, forma non linearizzata.
Prima di tutto devo stare attento a gestire tutto in non linearità massiccia, cioè non si può supporre che nulla sia piccolo per cui utilizzo a piene mani funzioni trigonometriche non linearizzate e funzioni anche ad esempio distanza tra due nodi in forma non linearizzata. Di base cosa faccio,
definisco le funzioni ausiliarie, distanza tra due punti (x_1;y_1)e (x_2;y_2)come la radice della somma dei quadrati, forma non linearizzata.
Se avessi bisogno di definire un seno e un coseno li si definiscono come:
 forma che regge anche a grosse rotazioni. Poi, definiamo la funzione rotazione angolare rispetto all'indeformata, definisco un polo (x_1;y_1), un punto P=(x_2;y_2)che definisce l'indeformato e il punto Q=(x_3;y_3)che definisce uno spostamento del punto P.
forma che regge anche a grosse rotazioni. Poi, definiamo la funzione rotazione angolare rispetto all'indeformata, definisco un polo (x_1;y_1), un punto P=(x_2;y_2)che definisce l'indeformato e il punto Q=(x_3;y_3)che definisce uno spostamento del punto P.
- $t=0$ quando $Q≡P$
- $-π<t<πa$ seconda dell'orientazione di $Q$
seguito da un controllo.


Adesso, posso andare a definire l'energia potenziale elastica dell'elemento, barra incernierata a telaio, nella maniera più semplice possibile, senza linearizzazione:
$$ U=1/2⋅k⋅((L_{def}-(L_{indef}))^2 + 1/2⋅s⋅(\alpha)^2 $$ dove $\alpha$ è l'angolo compreso tra la configurazione deformata e indeformata
Avremo :
- il punto (x_0 ; y_0)connesso a telaio;
- il punto (x_1 ; y_1)indeformata;
- e (x_1+u ; y_1+v) quando si deforma;
Ho definito una funzione lunghezza di segmento dato coordinate e U sarà indubbiamente l'energia potenziale elastica della molla estensionale sommata all'energia potenziale associata alla molla rotazionale, ovvero ½ per rigidezza rotazionale s per scostamento in rotazione, [definito come angolo tra il segmento corrispondente all'indeformata (x_0;y_0)-(x_1;y_1)e la deformata in (x_1+u;y_1+v)].
La matrice di rigidezza della struttura, se il sistema è non-lineare non è una costante in particolare, se ho un sistema non-lineare a un solo g.d.l ue disegno una caratteristica elastica non-lineareF, avremo che la rigidezza della struttura, definita come la tangente alla curva di equilibrio , non è una costante in ue nemmeno in F. La rigidezza in ogni punto sarà definita da una pendenza differente della curva corrispondente. Sostanzialmente mi accorgo che definire quelle matrici di rigidezza in non lineare diventa abbastanza complesso. Quindi mi conviene utilizzare quello che è il legame tra matrice di rigidezza e l'energia potenziale, che è stata opportunamente calcolata.
 La matrice di rigidezza tangente la definisco in funzione dell'energia potenziale elastica dell'elemento, in particolare:
$$
\underline{\underline{K}}_{T}
=
\underline{\underline{H}}(U)
=
\begin{bmatrix}
\frac{∂^2U}{∂u∂u} &\frac{∂^2U}{∂u∂v}\\
\frac{∂^2U}{∂v∂u} &\frac{∂^2U}{∂v∂v}\\
\end{bmatrix}
$$
La matrice di rigidezza tangente la definisco in funzione dell'energia potenziale elastica dell'elemento, in particolare:
$$
\underline{\underline{K}}_{T}
=
\underline{\underline{H}}(U)
=
\begin{bmatrix}
\frac{∂^2U}{∂u∂u} &\frac{∂^2U}{∂u∂v}\\
\frac{∂^2U}{∂v∂u} &\frac{∂^2U}{∂v∂v}\\
\end{bmatrix}
$$
in questa maniera risulta evidente anche per il teorema di schwarz che deve essere simmetrica. Praticamente definisco in maniera semplice il potenziale, e definisco sulla base del potenziale l'energia rigidezza. Quella matrice rigidezza è in una forma troppo complessa per essere scritta però la posso ricavare nell'intorno di ogni configurazione voluta. Quindi la posso trovare nell'intorno della configurazione scarica $[u=0;v=0]$ oppure posso farlo nell'intorno della configurazione caricata, ci metto uno specifico valore di u e v se presente nel grafico. Ad esempio nell'intorno della configurazione scarica la matrice di rigidezza definita come l'hessiana del potenziale è:
notiamo che è funzione di k, s , e delle coordinate.
Se voglio fare un esempio lo faccio qui;
La matrice rigidezza di un elemento barra con elemento elastico con rigidezza rotazionale s alla base, rigidezza assiale k, coordinate (0,0) per la cerniera e coordinata superiore (0;a) il secondo punto verticale con altezza a. Avremo questa forma:
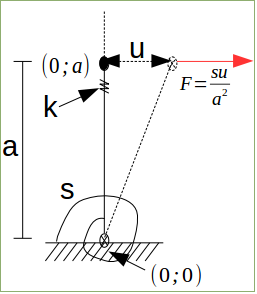
 che se si esegue un controllo è la matrice rigidezza nell'intorno della normale. Se ad esempio si vuole dare uno spostamento di entità u, dovremo applicare una forza F che vale: F=(s⋅u)/a^2
che se si esegue un controllo è la matrice rigidezza nell'intorno della normale. Se ad esempio si vuole dare uno spostamento di entità u, dovremo applicare una forza F che vale: F=(s⋅u)/a^2
dove u/aè la rotazione che moltiplicata per s da la reazione della molla torsionale (verso antioraria) e la forza al vertice dovrà generare una coppia (s⋅u)/a^2 ⋅ae si vede che la coppia applicata alla verticale e la coppia necessaria ad equilibrare la reazione elastica della molla sono uguali. E la stessa cosa per un ipotetico spostamento v applicato verticalmente richiede una forza v⋅kcapace di stendere la molla.
A questo punto, potrei calcolare le matrici di rigidezza tangenti in ogni punto del percorso di equilibrio, e così ad esempio potrei implementare un Newton-Raphson ad esempio, ma non è quello che si fa nei fem. Io adesso voglio implementare quelle procedure di analisi che utilizzano i fem nel predire uno stato di instabilità (o meglio di criticità della soluzione, buona per i piccoli spostamenti) , dato che abbiamo costruito un elemento e abbiamo la sua matrice rigidezza.
Data la matrice rigidezza tangente, che abbiamo visto, che è possibile scrivere nell'intorno di ogni configurazione di equilibrio, avremo due possibilità:
Possibilità A
Ho la matrice rigidezza tangente funzione di (u;v) procedo con un newton-raphson, analisi non-lineare standard. $$ → \underline{\underline{K}}_{T} (u,v) ∀u,v $$
Si può scrivere anche in maniera diversa, abbiamo il potenziale in funzione di (u,v) allora da questo possiamo trovare le reazioni elastiche associate all'elemento, il vettore reazione in funzione anch'esso di (u,v). $$ → U(u,v) → R(u,v)= \begin{bmatrix} \frac{∂U}{∂u} \\ \frac{∂U}{∂v}\\ \end{bmatrix} $$
Possibilità B Linearize Pre-Bukling analisis
Usata in un sacco di casi e soprattutto riguarda l’instabilità delle colonne di Eulero, ad esempio. Come funziona:
- Evita di eseguire il percorso di equilibrio con N-R
- La struttura viene sempre considerata nella configurazione indeformata
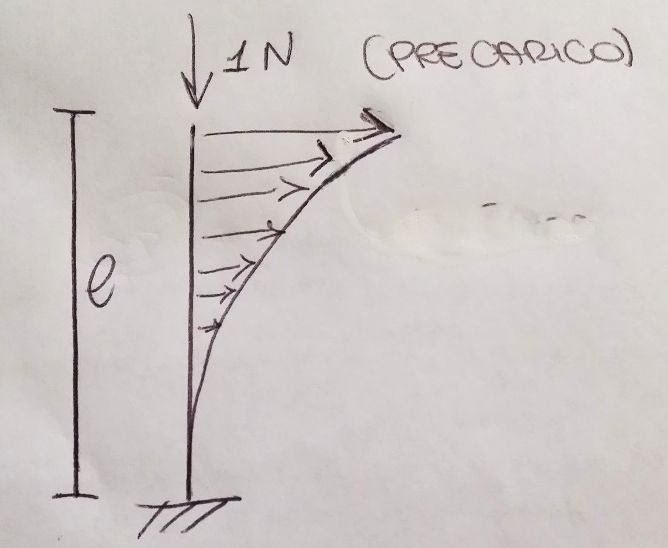
- Tuttavia la struttura indeformata viene considerata precaricata o pretensionata (ad esempio stato tensionale iniziale non nullo)
- Considero l’energia potenziale elastica strutturale funzione degli spostamenti ma considero anche il lavoro dal precarico (dove per precarico suppongo sia un semplice sforzo normale)
$$ U_{u,v} + L_{prec(u,v)} $$
La struttura indeformata va da $ (x_{0},y_o) $ a $ (x_1,y_1) $, ma la molla è precaricata da uno sforzo normale N.
La struttura, se la lascio in queste condizioni, non è in equilibrio e ci vorrà un carico esterno per bilanciare il precarico, però possiamo dire che la molla ha quella dimensione geometrica precaricata.
Mi accorgo che quando vado a spostare il nodo N, il sistema si allunga di una quantità $ Δl $. Il precarico (forza conservativa) si può immaginare come due forze che agiscono su due punti estremi del nostro elemento, essendo forze interne, tanto quanto le reazioni elastiche.
Quando vado a compiere lavoro su quell’elemento, ad esempio spostando quei nodi, il lavoro che compio va a incrementare l’energia potenziale elastica della struttura, quindi allungare la molla e pretensionare la molla , e in più va a far compiere lavoro alle forze interne di precarico. Questo precarico compie lavoro N*Δl.
Questo prodotto si può vedere in un altro modo essendo
$
N = σ_{0}⋅a
$
e
$
Δl=l⋅ε
$
Quindi il prodotto $ N*Δl = σ_{0}⋅ε⋅a⋅l $
Ossia questo ε è una deformazione dovuta agli spostamenti u e v che aggiungo rispetto alla configurazione indeformata; $σ_{0} ⋅ε$ è il lavoro compiuto sulla deformata dal precarico, mentre $a⋅l$ è il volume di una barra deformata a sforzo normale.
Quindi questo oggetto è anche uguale a
$$
L
=
N*Δl
=
∫_{V} \underline{σ}_{0}^T \underline{ε} dV
$$
che posso estendere a un corpo non a stato monoassiale.
La matrice di rigidezza tangente della struttura sarà uguale alla somma dell’Hessiano della funzione potenziale e l’Hessiano del lavoro del precarico:
$$
\underline{\underline{K}}_{T} = \underline{\underline{H}} (U) + \underline{\underline{H}} (L_{prec})
$$
La matrice $ \underline{\underline{H}}(U) $ la chiamiamo matrice di rigidezza associata al materiale, contiene sia $k$ che $s$ e si annulla se $k$ e $s$ sono nulli; mentre il contributo $ \underline{\underline{H}}(L_{prec}) $ è funzione del precarico, e si chiamerebbe matrice di rigidezza da precarico; entrambi sono calcolati nell’intorno di $ (u,v)=0$, cioè in configurazione indeformata. Con questo tipo di procedura non ho nessun bisogno di calcolare la deformata ma basterà calcolarmi lo stato di precarico.
Esempio: vado a calcolarmi la matrice rigidezza geometrica associata al precarico complessivo unitario, calcolata per primo nodo [0,0], per secondo [0,a] e per precarico in compressione -1, in rotazione 0. La matrice lega variazioni di carico con variazioni di condizione. Abbiamo una condizione iniziale pretensionata e precaricata da P, cosa succede se applico uno spostamento u da questa condizione?
$$ \underline{\underline{K}}^T \begin{bmatrix} \ Δu \\ \ Δv\\ \end{bmatrix} = \begin{bmatrix} \ ΔF_{x} \\ \ ΔF_{y}\\ \end{bmatrix} $$
Quest'ultima matrice tangente dell’intorno deformata che moltiplicata per la variazione di spostamento mi da la variazione del coefficiente di spostamento in funzione del coefficiente di carico.
Se $ \underline{\underline{K}}_{T} $ è singolare, succede che, a fronte di una variazione di carico nulla è ammessa una variazione di spostamento non nulla.
$$ \underline{\underline{K}}^T \begin{bmatrix} \ Δu \\ \ Δv \\ \end{bmatrix} = \begin{bmatrix} \ 0 \\ \ 0 \\ \end{bmatrix} $$
Vediamo quando questa matrice può essere singolare, cioè il determinante della matrice si annulla. Il determinante della matrice, dato dalla somma della matrice di rigidezza del materiale e la matrice di rigidezza del precarico, con precarico unitario, si annulla per un carico $ P=S/A $ , che è il carico critico, identificato precedentemente.
Vuol dire che nell’intorno della configurazione indeformata se $ P=S/A $ allora la matrice è singolare, per cui la soluzione non è unica ma abbiamo $ ∞^1 $ soluzioni.
In generale, un problema di Linearize Pre-Bukling si riduce a:
$$ [ \underline{\underline{K}}_{ELAST} + λ \underline{\underline{G}} ] | \underline{u} | = | \underline{F} | $$
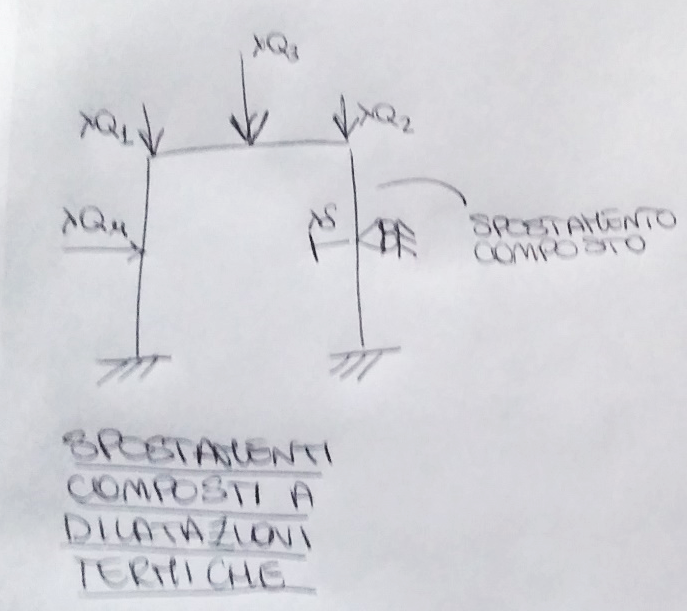
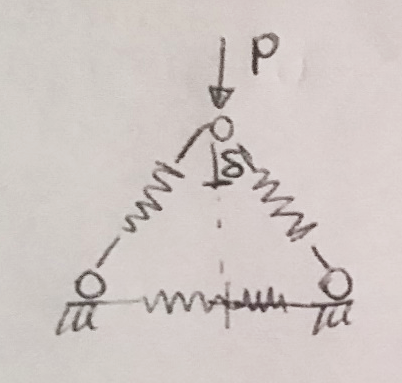
$λ$ è lo stato di carico preesistente sulla struttura, carico complesso a piacere che possono essere più di uno ma che tutti devono variare proporzionalmente ad un solo lambda. Quindi posso avere un sistema di carico più complesso, come il portale che segue
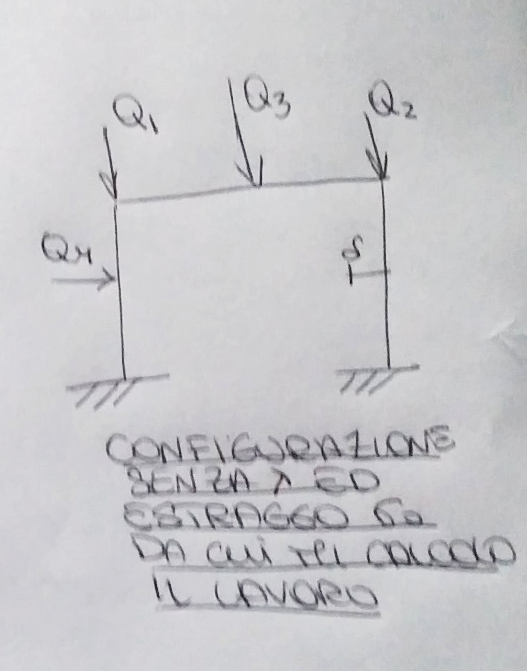
dove ho varie forze tutte scalate della stessa quantità lambda. Prendo il sistema senza il lambda e vado a rilevare lo stato di precarico della nuova struttura
e per ogni punto della struttura mi vado a calcolare il $ σ_{0} $. Noto il valore di $ σ_{0} $ mi vado a calcolare il valore del precarico, da cui calcolo l’Hessiano e infine il valore della mia matrice.
Ci chiediamo quando matrice
$
[
\underline{\underline{K}}_{ELAST} + λ \underline{\underline{G}}
]
$
è singolare. Questo è un problema agli autovettori e agli autovalori; quindi pongo il determinante uguale a 0
$$ | \underline{\underline{K}}_{ELAST} + λ \underline{\underline{G}} | $$
trovo i valori degli autovalori $λ_{i}$ e degli autovettori $ \underline{V}_{i} $ tali che
$$ [ \underline{\underline{K}}_{ELAST} + λ \underline{\underline{G}} ] \underline{V}_{i} = \underline{0} $$
Vuol dire che posso isolare delle coppie di scalature del precarico e forme di moto, tali per cui quelle forme di moto sono ammesse in quantità arbitraria senza necessità di introdurre un carico diverso da zero nel sistema.
Ovviamente risulterà che se prendiamo una colonna a cui è applicato un precarico pari a 1N, sulla cui base costruiamo $ K_G$ e facendo un analisi agli autovalori, risulterà che $ λ_i $ sarà uguale al primo carico critico euleriano
$$ λ_i = \frac{π^2 EJ)}{(4l^2} $$
Così abbiamo mostrato che avendo un elemento finito possiamo definire la sua matrice di rigidezza in forma lineare mentre per casi non lineari utilizziamo il metodo N-R.
Possiamo applicare questo tipo di analisi anche a una struttura composta da due molle, con rigidezza $ k_1 $ e $ k_2 $, con $ k_1 > k_2 $
La matrice rigidezza della struttura è uguale alla somma delle matrici di rigidezza; la matrice di rigidezza geometrica della struttura è uguale assemblaggio delle due matrici di rigidezza geometriche degli elementi, sottoposte a carico unitario. Anche in questo caso troviamo un carico critico che coincide con quello visto precedentemente. Questa procedura non funziona sempre e in questo caso particolare non lavora bene perché non stiamo parlando di un problema di biforcazione. La soluzione in questo caso è semplicemente non lineare. Il sistema ha reazione elastica nulla in indeformata e reazione elastica nulla quando le molle sono allineate, per cui la curva spostamento (δ) - carico applicato (P) ha un andamento del tipo:
In questo caso abbiamo un annullamento della matrice di rigidezza tangente.
Linearized Pre-Buckling Analysis:
Note per lo studio individuale
- struttura discretizzata in configurazione indeformata precaricata;
- dato un sistema di carichi/vincoli di cui alcuni potenzialmente non omogenei, calcolo lo stato di precarico con un precalcolo lineare elastico. Ottengo in questo caso uno stato tensionale $\underline{\sigma}^0 = \left[\sigma_x^0 \sigma_y^0 \sigma_z^0 \tau_{xy}^0 \tau_{yz}^0 \tau_{zx}^0\right]^T$, che nel caso dell'elemento puntone si riduce ad uno sforzo normale $N^0 = \sigma^0 A$;
- noto il precarico, calcolo la matrice di rigidezza “geometrica” o di “precarico” $K_{G}$ associata a tale condizione di precarico indotta dal sistema di carichi applicati sulla base del lavoro che tale precarico, supposto costante, compie sugli spostamenti infinitesimi a partire dalla configurazione indeformata.
- Il sistema deve essere considerato in grandi rotazioni (funzioni trigonometriche espanse in serie di taylor almeno al secondo ordine) al fine di poter estrarre la matrice di rigidezza “geometrica” o di “precarico”. Tale matrice scala scalando il precarico e quindi i carichi applicati.
- Compongo la matrice di rigidezza dell'elemento non precaricato (matrice di rigidezza relativa all'elasticità del materiale) con la matrice di rigidezza geometrica, scalata per un fattore $\lambda$
- ottengo una matrice di rigidezza combinata nella forma $ K = K_{el} + \lambda K_{G} $ e un sistema di equazioni di perturbazione dell'equilibrio iniziale nella forma $$ \left(K_{el} + \lambda K_{G}\right) \underline{\Delta u} = \underline{\Delta F} $$ ove $\underline{\Delta u}$ è una perturbazione della configurazione iniziale in termini di spostamento, in risposta ad una perturbazione \underline{\Delta F} delle forze esterne.
- nel caso la matrice di sistema risulti singolare, ovvero sia $\lambda_i$ t.c. $$ \det\left(K_{el} + \lambda_i K_{G}\right)=0$$, si ammettono soluzioni in termini di perturbazione agli spostamenti non nulla a fronte di un'assenza di perturbazione delle azioni esterne. Il problema si riduce ad un'estrazione di coppie di autovalori generalizzati $\lambda_i$ e autovettori $\underline{v}_i$ t.c. $$ \left(K_{el} + \lambda_i K_{G}\right) \underline{v}_i = \underline{0} $$.
- tale problema generalizzato agli autovalori/autovettori può essere ricondotto ad un problema agli autovalori “standard” premoltiplicanto per $K_{el}^{-1}$ (dovrebbe risultare invertibile in assenza di moti di corpo rigido residui) e procedendo ad un'inversione della forma dell'autovalore, ottenendo dopo semplici passaggi $$ \left( K_{el}^{-1} K_G - \mu_i I \right) \underline{v} = \underline{0} $$ ove $\mu_i = -\frac{1}{\lambda_i}$
- I fattori $\lambda_i$ sono fattori di amplificazione del precarico (e quindi del sistema di carico che lo ha generato) che rendono singolare la matrice di sistema e aprono a soluzioni distinte rispetto a quella prevista per evoluzione continua dalla condizione di piccoli carichi.
Forma alternativa implementata in MSC.Marc, in coda ad analisi nonlineari:
- Si considerano due condizioni di equilibrio carico/spostamenti distinte $\underline{P}_0,\underline{u}_0$ e $\underline{P}_1,\underline{u}_1$, tipicamente estratte da due step successivi del caricamento incrementale introdotto per agevolare il N-R.
- Si considerano le due matrici di rigidezza $K_0$ e $K_1$ associate a tali condizioni di carico.
- Si suppone un'evoluzione lineare della matrice di rigidezza con l'evolvere del carico, per cui si associa alla condizione di carico $\underline{P}^\lambda=\underline{P}_0+\lambda \left( \underline{P}_1 - \underline{P}_0 \right)$ la stima della matrice di rigidezza tangente come $K_t^\lambda = K_0 + \lambda \left( K_1 - K_0 \right)$.
- Si procede quindi in maniera analoga alla procedente andando ad impostare il problema agli autovalori generalizzato $$ \left(K_0 + \lambda_i \left( K_1 - K_0 \right)\right) \underline v_i = \underline{0} $$ da cui le coppie di fattore critico di amplificazione $\lambda_i$ e tangente al ramo di soluzione biforcato $\underline{v}_i$. Tale soluzione diventa repentinamente ammessibile in sovrapposizione a quella associata al ramo già percorso una volta raggiunto lo stato di carico $$\underline{P}^i=\underline{P}_0+\lambda_i \left( \underline{P}_1 - \underline{P}_0 \right)$$
Si usa chiamare primo carico critico il primo punto di biforcazione incontrato incrementando i carichi dalla condizione iniziale di sistema scarico (non precaricato). Non è detto sia il carico critico minore.
Materiale didattico
sviluppo matrice di rigidezza geometrica su elemento barra incernierata nonlineare.
Nonlinear Finite Element Methods, carlos.felippa@colorado.edu, capitolo 28.
test_form_content_ridim.imm_