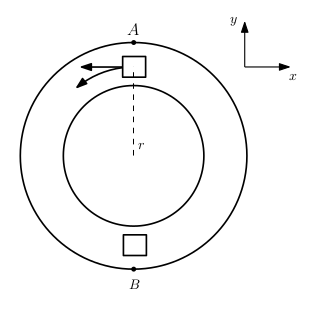
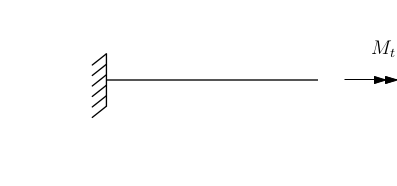
Se nei modelli non è possibile approssimare, uso le funzioni trigonometriche nello sviluppo completo $\left(\sin\theta\approx\theta \ \ e\ \cos\theta\approx0\right)$. Le funzioni trigonometriche non sono lineari, perciò danno la Non Linearità. Esempio: piccolo tubo incastrato a un estremo e con una coppia torcente all’estremità libera.

sorgente ipe

la faccia terminale:
sorgente ipe
La sezione ruota e la rotazione varia da un valore = 0 nell’incastro a un valore massimo nell’estremo. Viene preso ogni nodo al centro della sezione dello spessore; si sposta in due direzioni: - direzione tangenziale: per cui uso l’ipotesi di linearizzazione a piccole rotazioni; - direzione circonferenziale: nella componente y ha un termine dell’ordine di $\cos\theta $, che linearizzato è uguale a 0. Perciò mi muovo solo lungo la tangente. Detto AB il diametro iniziale e CD il diametro finale, traccio la deformata. Se nel tubo è inserito un manicotto, quest’ultimo è montato con gioco ma non ruota solidale al tubo. Il tubo ruotando fa aumentare il diametro. Secondo l’ipotesi lineare si crea interferenza a causa dell’allargamento del diametro del tubo.

Esempio trave caricata in estremità con un carico P:

sorgente ipe sorgente ipe

La sua deformata in forma linearizzata è un puro spostamento in direzione verticale. Se si aumenta il carico e poi lo si scala, si ottiene la deformata scalando lo spostamento per il lambda. In questa configurazione, la trave si è vistosamente allungata e perciò siamo in presenza di uno sforzo normale, cosa che in forma lineare non si verifica. Ogni tratto di trave nasce orizzontatale e subisce una rotazione (ottenuta muovendo il punto lungo la tangente) aumentando anche di estensione.

Per carichi molto elevati con materiale che può subire grandi deformazioni: la trave tende a divenire quasi verticale, quindi prevale lo sforzo normale rispetto al momento flettente.

sorgente ipe

Il materiale a un certo punto devia dalla linearità dando luogo a una curva ingegneristica sigma-epsilon (to stress to strain), monotona decrescente. Tale comportamento è non lineare perché per deformare ottengo una tensione non scalata. Non è detto che un comportamento non lineare sia non elastico. Se la curva è non lineare ma la deformata è pienamente reversibile, come ad esempio nel caso delle gomme, il materiale è elastico e reversibile ma non lineare.

Ipotizzo di avere una trave con un carico applicato all’estremità;

sorgente ipe

Ma sul punto mediano della trave, c’è la possibilità di un appoggio, tra la trave e l’appoggio ho g = gioco iniziale, mentre δ = spostamento sotto il carico.

Diagramma carico-spostamento della struttura: Aumento man mano il carico (variabile indipendente) durante la mia simulazione, mentre δ è la variabile dipendente.

sorgente ipe

Per piccoli carichi ( nell’intorno dello zero, carichi infinitesimi) : il gioco finito non viene annullato.

è come se non ci fosse l’appoggio. La pendenza $k_{1}$ segue la legge: $\frac{P}{k_{1}}=\delta$.

Poi avrò un livello di carico di transizione dal regime 1 al 2 $P\left(1\rightarrow2\right)$ —> condizione di sfioramento: I due punti si toccano ma senza trasferimento di carico ““sistema formula”” è una condizione singolare nello stesso istante.

Questo vale solo per il carico di transizione —> reazione di contatto. Poi il sistema va in appoggio: quindi si considera un appoggio intermedio.

Viene messo un carrello (no attrito) che si sposta in direzione normale al contatto fra i due corpi. Ho una reazione vincolare R. L’evoluzione continua è un tratto rettilineo con pendenza $k_{2}$, che è tipica del sistema.

$\frac{P}{k_{2}}=\delta$

Ho un sistema con comportamento lineare a tratti e rettilineo se esiste un g preesistente maggiore di 0. Se g = 0 inizialmente, per carichi positivi ho un comportamento di tipo 2 con $k_{2}$ e 1, per carichi opposti a quelli disegnati (negativi) ho comportamento di tipo 1 con $k_{1}$ e la transizione si ha nell’intorno del gioco. Secondo la convenzione dei segni:

Condizioni di Signorini

$$ \left\{\begin{matrix} R\geq0 \\ \ \ \ \ g\left(P\right)\geq0\ \ \ \ \ \ \ per\ \ \ evitare\ \ \ la\ \ \ compenetrazione \\ \ \ \ \ \ \ \ \ \ R\left(P\right)g\left(P\right)=0\ \ \ \ \ \ \ \ Condizione\ \ \ di\ \ \ ortogonalità \\ \end{matrix}\right. $$

Le tre condizioni devono valere in ogni punto.

Se introduco l’attrito e le leggi di Coulomb:

$\parallel\vec{\tau}\parallel\leq p \ f $

dove $p$ è la pressione di contatto al punto mentre $f$ è il coefficiente di attrito. L’attrito introduce fenomeni non lineari impliciti.

Caricamento proporzionale:

$\vec{\tau}\left(P\right)=\vec{\alpha} \ P $

$p\left(P\right)=\beta \ P$

è la condizione: metto

$\parallel\alpha\parallel\leq\beta \ f$

Indica che per un generico $ P > 0 $ è sempre verificato, mentre per $ P=0 $ mai. Questo vuol dire che ho la non linearità nella condizione di scarico.

I fenomeni di attrito introducono effetti di non linearità e le relative forme di dissipazione energetiche corrispondono a delle non-potenzialità (energetiche).

Per via dell’attrito e delle deformazioni plastiche, il comportamento del sistema è funzione della storia del carico e non dipende solamente dal carico istantaneo. Come esempio abbiamo considerato una sezione della membrana di un palloncino (di sezione a+da) alla quale viene applicata una pressione (p+dp). Il relativo carico risultante (p+dp)*(a+da) introdurrà un termine quadratico (da*dp) il quale introduce una non-linearità.

dispensa Progettazione Assistita con trattazione algoritmo N-R.

costruzione grafica per N-R 2d

costruzione grafica per N-R 1d

Si consideri un sistema lineare di n equazioni

R(u) = F (u)

nelle n componenti incognite del vettore u, con

R : u → Rⁿ , u ∈ C ⊆ R

F : u → Rⁿ , u ∈ C ⊆ R

funzioni vettoriali di variabile vettoriale.

Nel caso specifico della soluzione di sistemi di equazioni derivate dagli equilibri nodali di strutture discretizzate con metodo FEM, si definiscono le seguenti grandezze:

• u: vettore contenente le componenti di spostamento/rotazione nodale dalla configurazione indeformata (incognite);
• F(u): vettore contenente le componenti di forza/coppia nodale applicate dall'esterno sul sistema, supposte note per una data configurazione della struttura.
• R(u): vettore contenente le componenti di azione nodale (uguali e contrarie alle reazioni elastiche della struttura costretta in stato deformato) necessarie a mantenere la struttura in equilibrio nello stato deformativo associato al vettore spostamenti nodali u.

Nel caso particolare di sistema elastico lineare si ha che:

R(u) = K * u

con K matrice di rigidezza.

Si nota che tale interpretazione dei termini dell’equazione R(u) = F(u) è appropriata nel caso le condizioni al contorno siano alle sole forze. Nel caso in cui siano definiti vincoli di spostamento nodale imposto, alcune coppie di termini coniugati Ri(u)-Fi(u) risulteranno modificate in quanto all'equazione di equilibrio i-esima si sostituisce l’identità cinematica tra spostamenti incognito ed imposto.

Una scrittura alternativa prevede la definizione e l’annullamento di un termine di residuo

r(u) = R(u) − F(u) = 0

Tale scrittura permette di riassumere in un unico termine le variazioni in u di forze e reazioni elastiche, per cui risulta vantaggioso procedere con tale notazione.

Il metodo Newton-Raphson è costruito a partire dallo sviluppo in serie di Taylor al primo ordine dell’equazione 'r(u) = 0' di un punto di iterato i-esimo u^i, ossia:

r (u^*) = r (uⁱ) + Jr (uⁱ) · (u^* - uⁱ) + o (u^* − uⁱ) = 0.

Si considera il problema monodimensionale di un albero rotante con velocità Ω con una massa con eccentricità δ

Tale problema è prettamente “Non Lineare” infatti: per piccoli spostamenti lavora a flessione, mentre per spostamenti via via crescenti, tende a deformarsi come riportato nella figura di seguito.

L'eccessiva deformazione, ripercuotendosi anche sui vincoli, fa si che la trave lavori prevalentemente a trazione. La sua rigidezza, in questo caso, è molto maggiore nel caso di sollecitazione a pura flessione. Si parla in questo caso di Stiffening, ovvero di situazioni in cui la rigidezza cresce al crescere della deformazione.

Un altro aspetto da considerare è la forza centrifuga, dovuta alla massa eccentrica mantenuta in rotazione, che inizialmente vale:

F = m Ω² δ

e, dopo la deformazione:

F(u) = m Ω² (δ + u) R(u) = K u + g(u)

Nel caso particolare in esame “K = (6 E J)/lsup>3</sup><” In questo caso R(u) e F(u) sono funzioni scalari di variabili scalari.

Nel caso generale per risolvere il sistema di equazioni non lineari si procede come illustrato di seguito:

R(u) = F(u) sistema di equazioni non lineari

Si tratta il caso bidimensionale le cui proprietà si riscontrano nel caso ad “n” dimensioni.

Si accorpano le funzioni “R” ed “F” in una funzione residuo: r(u) = R(u) - F(u)

L'equilibro è soddisfatto se r(u) = 0 pertanto si risolve il sistema di equazioni non lineari

r₁(u₁,u₂) = 0 r₂(u₁,u₂) = 0

L'algoritmo di Newton - Raphson è un metodo iterativo con il quale si ricerca la soluzione approssimata della soluzione esatta incognita.

Come meglio sarà comprensibile nella trattazione del caso monodimensionale è un metodo simile al metodo delle tangenti.

Si sceglie un punto di partenza u₁ⁱ e u₂ⁱ, sia (u₁^*,u₂^*) la soluzione esatta del sistema, vale:

r₁(u₁^*,*u₂^*) = r₁(u₁ⁱ,u₂ⁱ) + [∂r₁/∂u₁] *(u₁^* - (u_i¹) + [∂r₁/∂u₂] * (u₂^* - u₂ⁱ) + o(u^*-u_i)

Per l'iterazione, togliendo l'infinitesimo, al posto della soluzione esatta si sostituisce la soluzione approssimata ponendo u^* = uⁱ⁺¹ lo stesso vale per la seconda equazione del sistema.

Quindi in forma vettoriale si risolve

r (uⁱ) + Jr (uⁱ⁺¹ - uⁱ) = 0

La matrice del sistema Jr è analoga alla matrice di rigidezza.

Una volta definito il passo di iterazione, a partire da uⁱ si va a risolvere l'equazione:

$$ u_{i+1} = u_i - J_r \backslash r(u_i) $$