cdm.ing.unimore.it

a cura di… Francesco Casini, Matteo Montagnani, Maria Giordano ed Edoardo Maletti

2018_04_27_esercitazione_al_marc_ver2.pdf

---

L’obiettivo della lezione odierna è quello di studiare gli effetti che un allungamento della dimensione assiale e l’infittimento della mesh del profilato soggetto a torsione, studiato negli scorsi laboratori, comporta sulla rigidezza a torsione dello stesso, sia nel caso di sezione sottile chiusa che aperta e per ognuno dei 2 casi imponendo dappirma che il warping sia libero e successivamente che sia impedito ad entrambi gli estremi.

Stabiliamo come diametro caratteristico quello di 120 mm ovvero la dimensione maggiore del profilato triangolare. In funzione di questa scelta si definiscono 3 tipologie di travi: una tozza, una media e una sottile. A ognuna di esse si associa una mesh di densità inversamente proporzionale in modo tale che il calcolo non sia troppo oneroso per i calcolatori e possa avvenire quasi istantaneamente. Sono disponibili 4 infittimenti delle mesh di ordine crescente nei file r1,2,3,4,8 del wiki. La lunghezza di metà del profilato iniziale è di 40 mm, in quanto esiste un piano di antisimmetria, dunque quella totale sarà il doppio; alla luce di questa ho che

• Tozza (40×2)x6=480 mm e vi associo la mesh più fitta r8
• Media (40×2)x12=960 mm e vi associo la mesh intermedia r4
• Sottile (40×2)x24=1920 mm e vi associo la mesh più lasca r2

ALLUNGAMENTO DELLA MESH

Procedo all’allungamento del profilato in direzione z globale, essendo la mia fila la n1 ho la trave sottile e procederò con questa, i risultati si trovano analogamente per gli altri casi Per allungare la mesh si procede allungando prima gli elementi già esistenti fino alla lunghezza voluta, ottenendo così una mesh strutturata, ma parecchio deformata. Per ottenere risultati buoni devo poi ripristinare la griglia iniziale dividendo la deformata in un numero di elementi pari alla scalatura degli elementi stessi, ripristinando le dimensioni iniziali. MAIN-MESH GENERATION-MOVE A questo punto mi viene chiesto di inserire nella voce SCALE FACTOR i valori della scalatura nelle 3 direzioni locali Per quanto detto scrivo la terna (1 ,1 ,24) la quale allunga la dimensione z degli elementi di 24 volte e al contempo di una volta, ovvero lascia invariate, le altre 2 dimensioni.

Questo processo viene fatto spostando i nodi, sebbene agisca poi sugli elementi, dunque devo cliccare NODES, al che mi viene chiesto di inserire i nodi sui quali effettuare l’operazione, si seleziona ALL-EXISTING. Ora, come detto, s’ottiene la struttura vistosamente deformata in direzione z, dunque, per riottenere la dimensione originale dei nodi divido quella la dimensione scalata di un fattore pari a quello di scalatura ottenendo una la griglia delle dimensioni iniziali, ma di estensione maggiore. MAIN-MESH GENERATION-SUBDIVIDE In alto ce la voce DIVISION, la quale chiede in input in quante parti dividere le 3 dimensioni dell’elemento generico. La pima indica la direzione locale ortogonale alla freccia sugli elementi, ovvero in direzione perimetrale , mentre la seconda indica quella ortogonale a questa, ovvero quella assiale e dunque la direzione che permette di raggiungere l’obbiettivo. La terza indica invece la dimensione di spessore che non è presente negli elementi piastra, dunque non ci interessa e posso lasciare il valore 1. Nei 2 precedenti invece metto 1 e 24, dopo di che, essendo questa suddivisione fatta sugli elementi, scelgo ELEMENTS e seleziono ALL EXISTING.

Alla fine di tutto ciò ho allungato la trave senza ridefinire alcuna boundary condition e senza cambiare la REB2 del corpo rigido. Ora, essendo state fatte queste modifiche alla mesh può succedere che alcuni nodi si siano slegati, per avere la continuità dei DOF e evitare vi siano nodi slegati faccio uno MAIN-MESH GENERATION-SWEEP e lasciando la tolleranza di default seleziono tutti i nodi con NODES-ALL EXISTING.

CALCOLO PER SEZIONE APERTA A LIBERO WARPING

Ora faccio un controllo sulle boundary condition e sulla guida di corpo rigido, verificando che siano stati rispettati i vincoli. MAIN-MESH GENERATION-LINKS-RBE2’S e controllo che sia libero il warping soltanto e non altri GDL che non rappresenterebbero fisicità. In particolare vedo che vi sono spunte solo nei DOF 1,2,6 che rappresentano gli spostamenti concessi, ovvero quelli proprio del warping. Non sono invece illuminati gli altri che riguardano lo spostamento fuoripiano z e le rotazioni entropiano theta e phi, ovvero si rendono rigidi solo certi gradi di libertà della faccia terminale della struttura Allo stesso modo controllo che le boundary condition di “guida di corpo rigido” siano rispettate come prima, ovvero che vi siano impediti tutti gli spostamenti e rotazioni tranne quella in z che è lineare con il corpo, al piano di antisimmetria, garantendo così l’assenza di moti rigidi della struttura e rendendo “meno” singolare la matrice rigidezza. Verificato ciò, posso procedere al calcolo della deformata. JOBS-PROPRIETIES

E lascio la richiesta dei risultati dello scorso calcolo Ora posso lanciare il calcolo RUN-SUBMIT

Ora ho una singularity ratio lontana da e-12 quindi la matrice è sufficientemente non singolare e i risultati dati sono attendibili. Il wall time dice il tempo di calcolo, che ci contiene anche gli scambi di dati con il disco e quindi tutte le operazioni ausiliarie. Per avere informazioni sui tempi di calcolo devo controllare i file di testo.

• Il file .mud è quello del modello.
• Il file .t16 è quello dei risultati.
• Il file .out lo apro con un editor di testo (pluma), qui la parte più interessante è la voce maximum

half-bandwidth, ovvero la larghezza di banda della matrice rigidezza, cioè la massima distanza tra un elemento e la diagonale. È anche indicato che essa è dovuto a un ponte elastico tra gli elementi 64 e 8176, opportunamente numerati in modo tale che la matrice risulti bandata il più possibile.

Sempre nel medesimo file è presente il numero di nodi totali nella mesh che moltiplicato per 6 mi restituisce il numero di gradi di libertà (gdl o DoF in inglese) del sistema permettendo così il calcolo del costo computazionale della matrice sia bandata che non, trovando che quello della bandata è sensibilmente più basso. Si nota come la banda sia circa un sesto di N. È presente anche una sezione di impiego memoria, tempo di calcolo e infine è presente il numero 3004 che indica che il calcolo è andato a buon fine.

• il file .log che funge da diario di lavoro ma in versione ristretta che dà soprattutto informazioni sulla memoria e sui tempi di calcolo oltre che al numero di iterazioni che in questo caso è una sola

non essendoci la dipendenza dal tempo.

• Il file .dat contiene invece i dati in input quali coordinate nodali connettività e proprietà varie.

Torno ora sul Marc e analizzo i risultati attraverso la opzione. Ora misuro la rotazione in Z del nodo master e lo confronto, in un foglio di calcolo, con la rotazione alla quale viene sottoposta la struttura con al suo estremo se si impone una rotazione per unità di lunghezza pari a 0.001 rad/mm, attraverso l*0.001=960*0.001=0.96 rad, come indicato nel foglio di calcolo. La rotazione al nodo centrale è effettivamente questa rendendo il modello verosimile. Per vedere questa rotazione sul file dei risultati seleziono in SCALAR la ROTATION Z specificando NUMERICS (in modo tale che vengano mostrati i risultati numerici e non a banda di colore) e guardo sul foglio dei risultati quella al nodo centrale, notando che vale proprio 0.96.

Ciò fatto posso procedere a ricavare dal modello la coppia di reazione al nodo master dovuta a quella rotazione imposta. Dividendo quella per la rotazione di prima si torva la rigidezza torsionale. Faccio allora SCALAR-RACTION MOMENT Z-NUMERICS e trovo il valore 22309.4. inserisco questo momento torcente misurato nel foglio di calcolo e ottengo automaticamente la rigidezza torsionale di 828,634857 mm^4. Noto poi che i 2 lembi del taglio hanno avuto un ampio scorrimento in z, abbassando notevolmente la rigidezza; infatti la struttura, spostandosi molto, sebbene in direzione z, mostra una elevata cedevolezza e di conseguenza una piccola rigidezza. Nella parte successiva del foglio di calcolo si è trovata la rigidezza torsionale teorica con Saint Venant che vale 832 mm^4. In basso si confronta questa con il valore teorico e si vede che la differenza è poca. Mettendo insieme tutti i risultati ottenuti con le mesh di diverso infittimento si nota che lo scostamento è molto basso, anche nel caso si usi una mesh molto grezza costituita da soli 2 elementi.

Questo è un caso particolare e la spiegazione del fenomeno è dovuta al fatto che la tensione tagliante component 12 of stress in preferred sistem è quasi costante, variando poco se non ai bordi. Per enfatizzare il fenomeno tolgo la NODAL AVERAGING dal plot andando in CONTROL BANDS-SETTINGS-EXTRAPOLATION-NODAL AVERAGING-OF. Essendo lo stato tensionale uniforme potrebbe, teoricamente, bastare un solo elemento per rappresentare l’intero stato tensionale, dunque l’infittimento della mesh non porta a sensibile miglioramento. È un caso abbastanza raro ma fa vedere come non sempre l’infittimento della mesh porti a un risultato migliore.

IMPEDIMENTO DEL WARPING PER SEZIONE APERTA

Voglio ora riempire le sezioni successive del foglio di calcolo andando a inserire i valori di rigidezza per il caso di warping impedito, sempre per la sezione aperta. Devo quindi imporre che i terminali siano completamente rigidi da entrambe le parti senza lasciare libero il warping. Riapro il file con il modello già allungato e blocco il warping agendo sui LIKS e sulle BOUNDARY CONDITION. MAIN-MESH GENERATION-LINKS-RBE2 e blocco tutti i gradi di libertà essendo ora il warping impedito e dunque non sia ammesso alcun moto distaccato da quello di corpo rigido. Si costituisce una sorta di incastro all’interno del rigido.

Adesso corpo rigido e deformabile sono completamente solidali tra loro. Nelle Boundary Condition avevo una condizione detta guida di corpo rigido che era stata pensata affinchè la struttura deformabile seguisse quella rigida solo nei moti lasciati liberi dal warping. Così facendo si impedivano rotazioni x,y e spostamento in z impediti che ora costituirebbero dei vincoli ridondanti in quanto sono già stati imposti all’altro estremo. Per questa ragione li tolgo, facendo si che non diano reazioni vincolari diverse da zero che costituirebbero delle non fisicità. Vado allora in BOUNDARY CONDITION seleziono la condizione “guida di corpo rigido” poi in PROPRIETIES e tolgo le spunte da quelle dai vincoli ridondanti detti sopra. Attivando spostamenti x e y significa che, essendo questi permessi dalla antisimmetria, nascerebbero moti di corpo rigido che traslerebbero l’intera struttura senza deformarla rendendo singolare la matrice K. Infatti uno spostamento del corpo rigido in x sarebbe consentito anche all’altro estremo, traslando rigidamente tutta la struttura.

Sono pronto ora a fare eseguire il calcolo. JOBS-RUN-SUBMIT Ancora una volta la matrice non è singolare dunque i risultati sono accettabili. Vado a vedere il file dei risultati e noto come il warping sia bene impedito agli incastri ma non appena ci si sposta da essi, questo fenomeno si ripresenti in modo vistoso essendo un moto naturale della deformata e dunque di possibile annullamento solo localmente. Controllo ancora la rotazione in z e vedo essere uguale a prima, come deve essere. Vado ora a vedere il valore della coppia di reazione con gli stessi passi di prima. Essa rappresenta la coppia da applicare per avere quella rotazione se il warping è impedito. Il valore di coppia è 49969 N*mm. Questo valore lo inserisco nel foglio di calcolo e, con la stessa rotazione di prima, mi calcolo la rigidezza torsionale per il caso di warping non libero. Noto che questa volta il discostamento dal valore teorico è di circa 22 volte. Dunque la sezione risulta molto più rigida quando le si impedisce il warping. Se supponessi di calcolare questo valore come una sorta di rigidezza apparente troverei un surplus dovuto completamente al non libero warping e non a un errore sistematico del programma di calcolo. Al variare della mesh, i risultati, anche nel caso di warping impedito, non variano considerevolmente anche nel caso di mesh molto lasca. Si ha invece una variabilità molto maggiore all’aumentare della lunghezza in quanto l’effetto dei bordi pesa percentualmente sempre meno.

Analizziamo ora lo stato tensionale e deformativo. Controllo gli spostamenti in z notando che sulla sezione terminale non sono uniformi ed in particolare sulla faccia terminale questi sono lineari e danno un disallinemtno rispetto al piano xy dando una deformata secondaria apparentemente flessionale Guardo lo stato tensionale attraverso la von mises al middle layer e vedo che esso ora non è scarico, contrariamente ai casi di warping libero. Nel punto di giunzione, in particolare, ho una von mises molto elevata che diventerebbe teoricamente infinita se si sfruttassero i risultati elastici. come si vede in figura

Questo è dovuto alla giunzione tra 2 diversi materiali, uno deformabile e uni infinitamente rigido. il valore non ha realmente senso in quanto si avrebbe snervamento primo. All’infittimento della mesh questo valore di picco cresce in quanto diventa sempre più preciso il calcolo locale di quella tensione. Questo è un risultato generale che vale ogni qual volta faccio una giunzione e mi fa capire come questa zona sia critica. Mi chiedo quale sia la tensione che maggiormente genera questo tipo di tensione e vado a graficare la components 11 of stress al meddle layer e noto che questa è dello stesso ordine di grandezza di della Von Mises

Si capisce allora come quando il warping è impedito la teoria esatta della trave crolli. Quest’ultima prevede infatti che lo stato tensionale sia costituito dalle sole tau e non prevede alcuna sigma che qui è invece la tensione maggiormente influenzante del problema. Al fine di analizzare in modo dettagliato lo stato tensionale è bene vedere la variazione delle tensioni sigma spostandomi dall’incastro alla mezzeria. Si nota che in mezzeria esse sono nulle per questioni di antisimmetria. Studiamo la legge con cui queste sigma calano con la quota assiale della trave. Passo alla forma indeformata e guardo la struttura di fianco dal lato del corpo rigido. Per graficare la sigma sul lato inferiore del taglio devo nascondere metà degli elementi in modo tale che riesca a campionare i nodi solo su una delle 2 metà, in senso longitudinale, della trave. Vorrei nascondere tuttii gli elementi sotto al taglio SELECT-ELEMENTS-ENDLIST faccio una selezione rettangolare degli elementi inferiori e faccio MAKE INVISIBLE, così facendo essi vengono nascosti e riesco in modo migliore a selezionare i nodi per costruire l’andamento della sigma lungo la direzione longitudinale. Riattivo poi i nodi in modo da poterli selezionare da PLOT-NODES mettendovi la spunta

Torno nel menu POSTPROCESSING-RESULT e vado a campionare la sigma con PATH PLOT. Devo definire il percorso che vada dall’incastro alla mezzeria e lo faccio attraverso il comando NODE PATH e seleziono in avanzamento nodi partendo dal primo in intorno del taglio avendo poi cura di selezionare l’ultimo in mezzeria (col tasto centrale si annulla un inserimento del nodo). Do un ENDLIST e il percorso viene memorizzato aspettando le quantità da monitorare in quel percorso. Per aggiungere gli assi faccio ADD CURVES-ADD CURVE; mi viene richeisto in ingresso l’asse X e rispondo ARC LENGHT, che è una ascissa curvilinea che varia da 0 al primo nodo selezionato al valore di mezzeria all’ultimo nodo selezionato. Come secondo asse seleziono la component 11 of stress in preferred sistem al middle layer, selezionando come prima. Per vedre il grafico devo scalare correttamente i valori della funzione sugli assi e per farlo schiaccio su FIT. A questo punto mi appare un grafico che mostra come l’andamento della sigma 11 sia lineare quasi ovunque se non nel tratto molto prossimo al bordo di corpo rigido.

Capisco allora che le tensioni variano linearmente in un sistema antisimmetrico e noto che sul lembo positivo vado da un valore negativo a zero e viceversa sul lembo negativo. Questo andamento lineare delle sigma deve essere duale nella metà inferiore di struttura, ovvero avere un andamento che passa da un valore positivo al bordo col corpo rigido a un valore nullo in mezzeria. Per ragioni di antisimmetria, deve essere duale anche l’andamento nella seconda metà simmetrica di struttura. Si capisce, allora, come la lunghezza sia il fattore determinante nel far calare il discostamento della teoria della trave esatta a torsione dal caso di warping impedito, in quanto la sigma 11 per trave molto lunga avrebbe un’ampia zona nella quale assumerebbe un valore vicino allo zero, facendo pesare meno il suo effetto disturbante sullo stato tensionale, rendendolo più vicino al nullo previsto della teoria esatta. Infatti, se la trave diventasse sufficientemente lunga, la rigidezza calcolata tenderebbe a convergere a quella ideale. Si vede nel foglio di calcolo come passando da 6 a 24 volte la lunghezza caratteristica si abbia un passaggio da un fattore che moltiplica la rigidezza ideale di 238 a uno 22 circa. Tuttavia, sarebbe necessaria, probabilmente una trave di uno due ordini di grandezza più lunghi rispetto a quella caratteristica, oggetto che risulta di difficile impiego nella pratica. Altra cosa da sottolineare è che ora la teoria della trave per essere valida deve avere un rapporto tra lunghezza e dimensione caratteristica molto maggiore dei 10/20 volte al quale si è abituati. Questo fa pensare che ciascuna banda della struttura venga deformata ad s come la trave disegnata in figura successiva

In questa immagine si nota come le sigma siano lineari e siano calino fino ad annullarsi in mezzeria e riprendano poi in modo antisimmetrico nella parte successiva. Per ora si tenga questa similitudine sebbene non sia del tutto spiegabile. Verrà poi approfondita in seguito nella teoria la sua spiegazione. Un'altra analogia della deformata può ottenersi con cerniere e manovelle disposte come in seguito, nella quale si suppone che le manovelle controruotino e impongano sposamenti verticali opposti ai 2 segmenti di trave alle quali sono collegate, dando di nuovo la deformata a s e le sigma lineari, antisimmetriche e nulle in mezzeria.

Da qui si può allo stesso modo derivare il warping libero aggiungendo sulle manovelle altre 2 coppie rotoidali che non fanno traslare le facce della trave opposte. Anche le sollecitazioni taglianti al middle layer non sono nulle come si può vedere plottandole da SCALAR e selezionando component 12 of stress middle layer e ottenendo un andamento piuttosto complicato del quale non cercheremo la legge per brevità.

La descrizione completa degli stati tensionali si lascia alla successiva lezione teorica, si tengano buone solo queste osservazioni sulle tensioni sigma 11 e su quelle taglianti. Dunque, il middle layer è contemporaneamente caricato sia da tau che da sigma; queste ultime non hanno un andamento parabolico come ci si aspetterebbe nel caso del risultato esatto della trave, bensì un andamento più complicato di cui al momento non si indaga troppo. Anche le superfici bottom e top sono caricate in modo piuttosto complicato, che si tralascia al momento per brevità.

ANALISI SEZIONE CHIUSA CON LIBERO WARPING

Riprendiamo allora il file della struttura iniziale già allungata per brevità. Ora dobbiamo fare in modo che il taglio divenga nullo. Per fare questo muovo i nodi della zona del taglio fino a farli coincidere. In Marc vado in MAIN-MESH GENERATION-MOVE e imposto nel fattore di scala i valori (1, 0, 1) in modo tale che i nodi selezionati vedano un fattore di scala di 0 andando di fatto a coincidere. Seleziono poi in COMBINED SELECTION sia NODES che POINTS e seleziono con selezione rettangolare i nodi prossimi alla zona del taglio. Dopo faccio endlist.

Faccio poi uno SWEEP con la tolleranza di default per evitare rimangano sovrapposti alcuni gradi di libertà della struttura. Dopodiché ripercorro il procedimento di prima con sezione chiusa, ovvero controllo che il warping sia libero in RBE2 e in BOUNDARY CONDITION e in seguito faccio RUN per far partire il calcolo, esattamente come fatto per la sezione aperta. Una volta fatto ciò, vado nel file dei risultati per controllare i valori rotazione e di coppia di reazione in modo tale da calcolare la rigidezza. Mi accorgo che selezionando ROTATION Z e impostando NUMERICS la rotazione è la medesima (0.96 rad) dunque il modello è accettabile. Vediamo ora quanto vale la coppia di reazione selezionando nel file dei risultati in SCALAR la REACTION MOMENT Z e impostando ancora NUMERICS per vedere i risultati sotto forma di valori numerici.

Trovo un momento di reazione pari a 1.39024e+7, ovvero 2 ordini di grandezza in più rispetto alla versione aperta, risultato che è lecito aspettarsi in quanto le sezioni chiuse sono molto più rigide di quelle aperte. Questo diverso risultato deve imputarsi al fatto che ora, come si può vedere dal modello, lo spostamento in z differenziale tra i 2 lembi tagliati non è più possibile a causa della continuità del materiale. Si vede allora che non essendoci spostamento elevato in z, in qualche modo, la cedevolezza della struttura è molto minore rispetto al caso al caso di sezione aperta, dunque la rigidezza sarà inevitabilmente molto maggiore.

Ancora noto che per il warping libero la rigidezza calcolata con le formule di Bredt, ovvero quella esatta con la teoria della trave è molto vicina a quella trovata dal FEM

Questo mostra, dunque, come nel caso di warping libero la teoria della trave sia valida.

ANALISI DI SEZIONE CHIUSA CON WARPING IMPETIDO

Passo ora al caso di warping impedito per sezione chiusa. Chiudo il file dei risultati e nel modello semplicemente impongo i vincoli di no warping attraverso il totale vincolamento del corpo rigido RBE2, ovvero rendendo completamente solidale la struttura al rigido spuntando tutti i gradi di libertà e attraverso le BOUNDARY CONDITION togliendo gli spostamenti in z e le rotazioni x e y nella condizione di “guida di corpo rigido”. Vado in JOBS-RUN-SUBMIT facendo eseguire il calcolo e ottengo, con il medesimo procedimento di prima una coppia di reazione pari a 1.39484 e+7, ovvero una rigidezza torsionale molto simile a quella del warping libero. Nel foglio di calcolo scrivo tutti i valori dei rapporti tra rigidezza nel caso di warping libero o impedito notando che la differenza è poca per la sezione chiusa, sia al variare della mesh che della lunghezza. Con quest’ultima, tuttavia, si ha ancora una maggiore mutevolezza.

Plottando le tensioni sigma 11 al middle layer notiamo come non vi siano più i picchi tensionali all’incastro mostrati precedentemente Posso allora concludere che la variazione della rigidezza all’impedimento o no del warping sia un effetto molto marcato per le sezioni aperte, mentre sia trascurabile per sezioni in parete sottile chiuse.

Si capisce allora come le sezioni chiuse sia migliori nel comportamento a torsione in quanto hanno 2 vantaggi  Sono di 2 ordini di grandezza più rigide, e quindi a pari peso della struttura si hanno prestazioni molto maggiori  Non danno problemi di picchi tensionali al cambio di materiale, facendo sì che le giunzioni non cricchino o snervino. Di solito ai cambi di materiale posso avere cordoni di saldatura o incollaggi che dovrebbero reggere il picco tensionale (solitamente qui già più critico), mettendoli in ginocchio, in particolare per carichi di tipo ciclico affaticante.

CALCOLO ANALITICO DELL’EFFETTO DEL WARPING PER SEZIONI APERTE (effetto Vlasov)

Proviamo ora a fare una stima della lunghezza che deve avere la trave affinché il warping sia trascurabile. Consideriamo la formula sul wiki che descrive la trave alla Vlasov, ovvero considerando gli effetti del warping impedito cosa che non viene fatta nella teoria di De Saint Venant

$$ [2 \theta] = \frac{M_t [2l]}{G K_\mathrm{t}} \left( 1 - \frac{2 d}{[2l]} \tanh\left( \frac{[2l]}{2 d} \right) \right) $$

Dove theta indica la semirotazione della sezione, l la lunghezza di mezza struttura e d è una dimensione caratteristica che possiamo definire come

$$ d^2 =\frac{E C_\mathrm{w}}{G K_\mathrm{t}} $$

Dove Cw è una particolare proprietà della sezione che non dipende dal coefficiente di Poisson e il denominatore è la rigidezza a libero warping. Nella formula di Vlasov, si vede che il termine moltiplicativo fuori dalla graffa rappresenta la rotazione della sezione calcolata con la solita teoria della torsione e il fattore 1 nella graffa indica proprio questo contributo. Il successivo fattore, anche esso moltiplicato per la rotazione della teoria della trave classica, rappresenta la componente di impedimento del warping sulla rotazione, il quale che genera forze di taglio dovute alla deformazione a S descritta precedentemente dalla figura con le coppie rotoidali. I 2 contributi possono vedersi (di solito in bibliografia sono mostrati per la sezione a doppia T) come: il primo, dovuto a De Saint Venant, descritto da una distribuzione locale a farfalla delle tau che genera una densità, sulla sezione, di momenti torcenti infinitesimi applicati e una seconda, dovuta a Vlasov, pensata come 2 forze di taglio che generano la restante parte di momento torcente che equilibra quello complessivo applicato ai terminali della struttura. Dal punto di vista deformativo la prima si imputa alla torsione pura con warping libero e la seconda alla deformata a S dovuta al warping impedito, come se vi fossero le 2 coppie rotoidali.

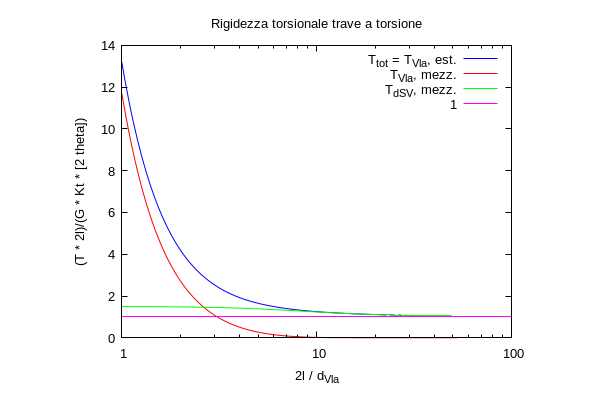
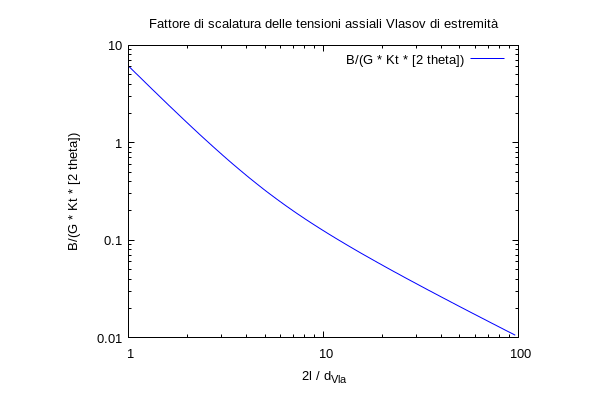
Il secondo contributo diventa dominante quando si impedisce il warping, mentre quando ciò non avviene si ha un effetto trascurabile del fenomeno. Quando il warping è impedito il termine riduce la rotazione a pari momento o, analogamente a pari rotazione richiede un maggiore momento torcente per generarla, all’atto pratico rende più rigida la struttura, spiegando in modo analitico quanto accade nel caso della sezione aperta dove si ha una rigidezza molto maggiore. Questo irrigidimento a warping impedito viene usualmente detto “effetto Vlasov”. Notiamo come l’influenza del secondo termine non sia costante ma dipenda dalla lunghezza della trave (diminuisce al suo crescere) e dalla dimensione caratteristica (aumenta al suo crescere). C'è pertanto una dipendenza dell’effetto del termine di warping bloccato che dipende dal rapporto tra dimensione caratteristica e lunghezza della trave. Confrontando la lunghezza caratteristica con quella della trave si stabilisce se il contributo sia importante o no ai fini della trattazione del problema, ovvero mostrando se l’effetto Vlasov è o no considerevole una volta bloccato il warping. Possiamo allora valutare quanto sia rilevante l’effetto Vlasov nel nostro profilato valutando il valore della lunghezza caratteristica nell’equazione sopra, in quanto conosciamo tutti i dati fuorché il d, che come detto ci dà un’idea di quale sia l’entità dell’irrigidimento. L’equazione è, tuttavia, trascendente in d. Una volta trovato, si costruiscono dei diagrammi con in ascissa il rapporto 2*l/d e in ordinata il rapporto tra le rigidezze a warping impedito e libero. Il grafico è riportato nella figura seguente

Si nota come al valore di 100 tra 2*l/d la differenza sia praticamente nulla con rapporto tra le rigidezze pari all’unità. Possiamo allora ricavare il d procedendo nel foglio di calcolo con il metodo di Newton per risolvere l’equazione trascendete sopra. Nel foglio di calcolo inserisco direttamente il fattore di amplificazione associato alla rigidezza Vlasov, ovvero il rapporto tra la rigidezza calcolata nel caso di warping impedito e nel caso di warping libero. Nel mio caso questo vale 22.39, nel caso della mesh e della lunghezza svolta dal professore questo rapporto è pari a 238,61268. Inserisco poi il doppio della lunghezza del tratto considerato ovvero la lunghezza totale della trave 2*l. nel mio caso viene 1920 mm e nel caso del professore 480 mm. Il calcolo non parte a causa della non implementazione della funzione secante iperbolica nel nostro open office, si rimanda alla prossima lezione lo svolgimento effettivo del calcolo numerico. Nel foglio del professore svolgendo il calcolo si ottiene che per avere un effetto Vlasov trascurabile bisogna avere una trave di lunghezza di circa 15 volte la lunghezza caratteristica.

RIASSUNTO E CONCLUSIONI

Facciamo un breve riassunto della lezione, sottolineando i soli passaggi fondamentali e le conclusioni che essi ci permettono di trarre. Si è considerata inizialmente la sezione aperta e vi si è applicata una rotazione imposta e precalcolata funzione della lunghezza della trave soltanto. Da questa si è trovata col modello FEM la coppia torcente che questa genera per ragioni elastiche ai terminali. Facendo il rapporto coppia/rotazione ho trovato la rigidezza che, confrontata con quella esatta della teoria, mi ha confermato come i risultati analitici sia molto buoni per il caso di libero warping in sezione aperta. Qui abbiamo visto che l’infittimento della mesh non porta a grossi benefici sui risultati. Si passa poi all’impedimento del warping in sezione aperta e, con gli stessi procedimenti, notiamo una rigidezza molto maggiore dovuta un irrigidimento da warping che in seguito si studia analiticamente con la teoria di Vlasov. In questo caso l’infittimento della mesh non porta a sostanziali benefici sui risultati, mentre l’allungamento della trave sì. Questo è dovuto al fatto che nascono delle tensioni non sigma non previste dalla teoria della trave classica che sono lineari con la lunghezza e, nel caso di trave lunga, vanno via via diminuendo il loro effetto sulla deformata facendo tendere alla soluzione classica al divergere della lunghezza. Si passa poi alla sezione chiusa e, con procedimenti del tutto analoghi si trova che la rigidezza in caso di warping inibito o no è circa la stessa, mostrando che l’irrigidimento da warping è un fenomeno ristretto alle travi in parete sottile aperta. Inoltre, si vede come la rigidezza della sezione chiusa sia molto maggiore di quella aperta, a causa del fatto che non sono più possibili i vistosi spostamenti in z della zona del taglio rendendo il tutto meno cedevole. Infine, si è studiata l’equazione di Vlasov per la torsione di trave aperta sottolineando come il secondo termine segnali l’irrigidimento a warping impedito in funzione del rapporto tra una specifica dimensione caratteristica entropiano e la lunghezza complessiva fuoripiano della trave. Da qui si è costruito un grafico che in funzione del rapporto di cui sopra mostra il surplus di rigidezza imputato al non libero warping, notando che l’effetto svanisce solo per travi molto lunghe.

profilato_a_torsione_r0_l1_aperto_v009.mud

profilato_a_torsione_r1_l1_aperto_v009.mud

profilato_a_torsione_r2_l1_aperto_v009.mud

profilato_a_torsione_r3_l1_aperto_v009.mud

profilato_a_torsione_r4_l1_aperto_v009.mud

profilato_a_torsione_r8_l1_aperto_v009.mud

---

Profilati a sezione sottile chiusa, vari step di raffinamento

profilato_a_torsione_r0_l1_chiuso_v009.mud

profilato_a_torsione_r1_l1_chiuso_v009.mud

profilato_a_torsione_r2_l1_chiuso_v009.mud

profilato_a_torsione_r3_l1_chiuso_v009.mud

profilato_a_torsione_r4_l1_chiuso_v009.mud

profilato_a_torsione_r8_l1_chiuso_v009.mud

---

Foglio di calcolo per l'elaborazione dei risultati

foglio_di_calcolo_rigidezza_torsionale_trave_2018_v002.ods

---

Altro

profilato_a_torsione_r8_l1_aperto_nowarp_v009.mud

vlasov_torsion_cw_da_fem_nr.wxmx

Formula rotazione relativa corretta per termine Vlasov, warping impedito ad ambo i terminali;

$$ [2 \theta] = \frac{M_t [2l]}{G K_\mathrm{t}} \left( 1 - \frac{2 d}{[2l]} \tanh\left( \frac{[2l]}{2 d} \right) \right) $$

qui $[2l]$ è la lunghezza totale della trave, $[2\theta]$ è la rotazione complessiva relativa, e $d$ è la lunghezza caratteristica associata all'effetto Vlasov per la specifica sezione

$$ d^2 =\frac{E C_\mathrm{w}}{G K_\mathrm{t}} $$

$C_\mathrm{w}$ è una costante caratteristica della sezione, meno intuitiva ma più storicizzata della lunghezza caratteristica $d$ qui utilizzata; $C_\mathrm{w}$ non dipende dal coeff. di Poisson del materiale. $K_\mathrm{t}$ è il modulo di rigidezza a torsione della sezione, calcolata secondo la teoria classica a libero warping (de St. Venant).

---

Modelli a fine lezione

profilato_a_torsione_r8_l06_aperto_v010.mud

profilato_a_torsione_r8_l06_aperto_nowarp_v010.mud

profilato_a_torsione_r8_l06_chiuso_v010.mud

profilato_a_torsione_r8_l06_chiuso_nowarp_v010.mud

---