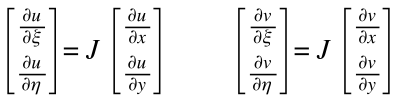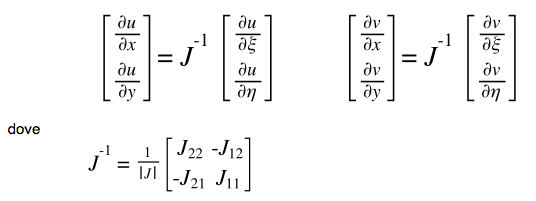La quadratura gaussiana è una tecnica di risoluzione per integrali definiti, che fornisce risultati esatti per integrazione di polinomi e, a parità di punti di integrazione, è più accurata della formula di Simpson. La formula consiste nel calcolo di un integrale definito tra gli estremi -1 e 1, in modo da poter annullare, come si vedrà in seguito, i termini di grado dispari dei polinomi. In caso non si abbiano già come estremi di integrazione -1 e 1 si agirà preventivamente con uno o più cambi di variabile e di conseguenza col cambio degli estremi, riconducendosi a un caso come quello prima descritto.

Esempio: polinomio di primo grado

Prendiamo a scopo esemplificativo un semplice polinomio di primo grado:

f(x) = a₀ + a₁x

esso, sviluppato tra gli estremi -1 e 1 da come risultato:

Il metodo di Gauss, invece di risolvere l'integrale come visto sopra, prevede di trovare una funzione w_i (peso) tale che wi moltiplicato f(x_i) dia come risultato quello appena ottenuto svolgendo il calcolo. Graficamente significa trovare la media integrale della funzione nell'intervallo (-1,1).

Scrivo quindi l'uguaglianza appena imposta:

2a₀ = w₁ f(x₁) = w₁ (a₀ + a₁x₁)

Tuttavia la relazione posta in tal modo ha infinite soluzioni, dal punto che presi a₀ e a₁ posso scegliere in infiniti modi diversi w₁ e x₁.

Per avere un'unica soluzione scrivo la funzione residuo, definita come:

R = a₀ ( w₁ - 2)+a₁ w₁ x₁

Derivo la formula appena scritta prima rispetto ad a₀ poi rispetto ad a₁, ottenendo il sistema di equazioni indipendenti:

da cui consegue w₁=2 e x₁=0, che come si nota è lo stesso risultato che ci si aspettava e vale per ogni polinomio di primo grado.

Esempio: polinomio di terzo grado

Si ragiona in maniera esattamente analoga all'esempio appena visto. Si prenda ad esempio il polinomio:

f(x) = a₀ + a₁x + a₂x² + a₃x³

Svolgendo l'integrale tra gli estremi -1 e 1 risulterà quindi:

Come si osserva i termini con esponente dispari si elidono grazie all'integrazione compiuta tra -1 e 1.

Per la risoluzione con Gauss, a differenza di prima non mi basta un solo punto di Gauss (w_i,x_i) come visto in precedenza, ma 2 punti, dato che ho 4 coefficienti. Scriveremo quindi in questo modo:

Scrivendo la funzione residuo si avrà:

Avendo quattro incognite, si deriva la funzione R in tutte, ottenendo il sistema di equazioni seguente:

Posso ricavare facilmente dalla seconda equazione il valore di w₂:

w₂ = −w₁ (x₁/x₂

Sostituendo questo nella prima equazione si ottiene:

Risostituendo nell' espressione di w₂ trovata prima si avrà che:

Si sostituisce ora alla quarta equazione le espressioni di w₁ e w₂, arrivando a trovare:

−x₁² + x₂² = 0 da cui consegue che x₁ = −x₂

dato che non posso avere punti coincidenti. A questo punto si puo risolvere completamente il sistema sostituendo quest ultimo risultato nella terza e nella seconda equazione del sistema, ottenendo che:

che sostituiti nell'espressione iniziale (con un po' di algebra) forniscono esattamente lo stesso risultato dato dallo svolgimento dell'integrale.

Esempio: polinomio di secondo grado

Il caso di polinomio di grado pari (si prenda per semplicità quello di grado 2), pone un problema: quanti punti di Gauss mi servono per determinare in modo perfetto l'integrale? Prendiamo il polinomio:

f(x)=a₀ + a₁x + a₂x²

Se si sceglie di sviluppare con 1 o 2 punti di gauss si ottengono i risultati qui di seguito:

Che danno rispettivamente I risultati visti in precedenza per i polinomi di grado 1 e 3.

Si nota che le formule che si ottengono come risultato sono ben diverse. Esiste una regola che lega il numero di punti di Gauss all'accuratezza del metodo:

VERSIONE ERRATA

“presi n punti di gauss, posso avere accuratezza perfetta per polinomi fino al grado 2n+1”

VERSIONE CORRETTA

“presi n punti di gauss, posso avere accuratezza perfetta per polinomi fino al grado 2n-1”

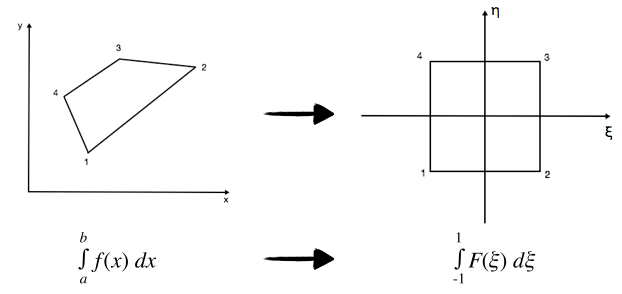
La teoria dell’elemento isoparametrico è una teoria che permette di affrontare un problema, anche relativamente complesso, in modo più semplice e immediato. La si può pensare come ad una “lente speciale” che prende l’elemento finito (mesh) in esame, lo deforma così che andrà da -1 ad 1 in un piano ξ-η, associandosi così alla quadratura gaussiana, al che ci si calcola la matrice di rigidezza e poi si torna nello spazio reale. In questo modo quindi è come se, piuttosto che avere a che fare con un elemento quadrangolare disposto in modo generico nel piano, si abbia a che fare con un banale elemento quadrato, centrato in (0,0) e di lato 2. Quest’ultimo prende il nome di Master Element.

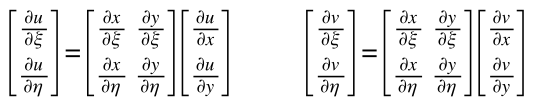
Quindi i passaggi di base sono quelli di effettuare un cambio di variabili, portarmi nel piano ξ-η, calcolare lì la matrice di rigidezza con il mio elemento semplificato e quella ottenuta sarà valida anche quando torno nel piano reale (“isoparametrico”). Si tratta quindi di calcolare un integrale dell’elemento attraverso una trasformazione che ci permette di passare da uno spazio all’altro: ci sarà infatti una matrice di trasformazione, detta Jacobiano. Cominciamo dagli spostamenti. Si scrivono le coordinate globali x e y in una forma per cui, sostituendo le coordinata locali (±1, ±1) del nodo, si ottiene la rispettiva coordinata nodale a noi già nota dalla mesh.

VERSIONE ERRATA!!!

VERSIONE CORRETTA $$ x= \frac{1}{4}\left(1-\xi\right)\left(1-\eta\right) x_1 + \frac{1}{4}\left(1+\xi\right)\left(1-\eta\right) x_2 + \frac{1}{4}\left(1+\xi\right)\left(1+\eta\right) x_3 + \frac{1}{4}\left(1-\xi\right)\left(1+\eta\right) x_4 $$

Si può notare che se si sostituiscono ad ξ e η i valori di un nodo, ad esempio 1 e -1 del nodo 2, si ottiene x = x2, effettuando così il cambio di variabile. In modo del tutto analogo sarà per y:

$$ y= \frac{1}{4}\left(1-\xi\right)\left(1-\eta\right) y_1 + \frac{1}{4}\left(1+\xi\right)\left(1-\eta\right) y_2 + \frac{1}{4}\left(1+\xi\right)\left(1+\eta\right) y_3 + \frac{1}{4}\left(1-\xi\right)\left(1+\eta\right) y_4 $$ Si osservi che si ha una funzione “di forma” lineare per gli assi ξ e η: bloccato cioè uno dei due, diventa lineare per l’altro. A questo punto si comprende appieno il perché del nome isoparametrico (“di uguale parametro”): le stesse funzioni di forma appena usate per il passaggio dalle coordinate locali a quelle globali, vengono utilizzate per definire gli spostamenti nodali, incogniti:

$$ u= \frac{1}{4}\left(1-\xi\right)\left(1-\eta\right) u_1 + \frac{1}{4}\left(1+\xi\right)\left(1-\eta\right) u_2 + \frac{1}{4}\left(1+\xi\right)\left(1+\eta\right) u_3 + \frac{1}{4}\left(1-\xi\right)\left(1+\eta\right) u_4 $$

$$ v= \frac{1}{4}\left(1-\xi\right)\left(1-\eta\right) v_1 + \frac{1}{4}\left(1+\xi\right)\left(1-\eta\right) v_2 + \frac{1}{4}\left(1+\xi\right)\left(1+\eta\right) v_3 + \frac{1}{4}\left(1-\xi\right)\left(1+\eta\right) v_4 $$

Definiti gli spostamenti, passiamo quindi alle deformazioni.

Ricordiamo che ε = Bδ, con deformazioni generalizzate e δ spostamenti. In particolare si ha che, considerando ad esempio la sola derivata di u rispetto ad x (per l’altra derivata è analogo), questa è definita come:

$$ \frac{\partial u}{\partial x} = \frac{\partial u}{\partial \xi} \frac{\partial \xi}{\partial x} + \frac{\partial u}{\partial \eta} \frac{\partial \eta}{\partial x} $$

e da com’è stato definito, calcolare la derivata di ξ rispetto ad x risulta essere abbastanza

difficoltoso. Tra l’altro, non vale neanche la proprietà di reciprocità, essendo

Si tratta quindi di riuscire a superare lo stesso problema nelle nostre coordinate ξ ed η. Il nostro obiettivo è quello di passare da in modo tale da potere sfruttare la quadratura gaussiana, che ben si sposa con la risoluzione FEM. Non potendo però sfruttare l’uguaglianza tra le derivate vista sopra, andiamo a scrivere il problema in una forma alternativa; in particolare si ha:

in modo tale da non avere più il problema di dovere derivare la ξ o η rispetto a x ed y. In forma matriciale questa, e analogamente per la v, si scrivono come:

Si può notare che tra le due espressioni, si và a scambiare semplicemente la v con la u, mentre la matrice 4×4 resta invariata. Le deformazioni hanno quindi una matrice in comune ed essa prende il nome di Jacobiano, J. Di fatto quindi si ha un legame del tipo:

Gli elementi dello Jacobiano si calcolano sfruttando la trasformazione usata inizialmente; nello specifico si ha che:

$$ J_{11}= - \frac{1}{4}\left(1-\eta\right) x_1 + \frac{1}{4}\left(1-\eta\right) x_2 + \frac{1}{4}\left(1+\eta\right) x_3 - \frac{1}{4}\left(1+\eta\right) x_4 $$

e così anche per gli altri tre componenti. Definiti quindi x1, x2, x3 e x4, la matrice è definita. A questo punto, potendo scrivere la matrice J ed essendo il nostro obiettivo quello di calcolare le derivate di u e v rispetto x ed y, basta manipolare le espressioni matriciali scritte sopra e ottenere così i termini desiderati.

con |J| determinante dello jacobiano. Di fatto esso varia con x1, x2, x3 e x4 quindi, in funzione delle coordinate prese, si potrebbe anche avere un determinante nullo. In questa eventualità non si potrebbe procedere con i calcoli; allora la fattibilità della trasformazione dipende proprio da come si fà l’elemento, che risulta essere quindi un punto abbastanza delicato della trattazione. In caso negativo infatti si andrebbe infatti in “instabilità numerica” e il FEM non sarebbe in grado di effettuare il calcolo (che “esplode”). Tutto ciò porta a sottolineare che la stabilità di un calcolo lineare è dovuta solo alla mesh (si parla di “bontà della mesh”) che và quindi fatta con giudizio. Siamo a questo punto in grado di definire l’espressione numerica della trasformazione scritta in modo incompleta nello specificare l’obiettivo al quale si mirava. In particolare si conclude che, da un punto di vista numerico:

la scrittura sopra proposta è valida solo nel caso l'elemento sia rettangolare con lati paralleli agli assi, caso particolarissimo e quindi poco interessante; in generale abbiamo

$$ \iint_{A} B^{T}DB dA = \int_{-1}^{+1}\int_{-1}^{+1} B\left(\xi,\eta\right)^{T}DB\left(\xi,\eta\right) \left|J\left(\xi,\eta\right)\right|d\xi d\eta $$

ove l'integrale è da intendersi svolto per integrazione gaussiana, ossia

$$ \iint_{A} B^{T}DB dA = \int_{-1}^{+1}\int_{-1}^{+1} B\left(\xi,\eta\right)^{T}DB\left(\xi,\eta\right) \left|J\left(\xi,\eta\right)\right|d\xi d\eta = \sum_{i=1}^{m} w_{i} B\left(\xi_i,\eta_i\right)^{T}DB\left(\xi_i,\eta_i\right) \left|J\left(\xi_i,\eta_i\right)\right| $$

Nel caso di elemento normalmente integrato (2×2 punti di integrazione in $\xi$,$\eta$) ho $ m=4 $, $w_i=1$, $i=1\ldots4$

$$ \begin{eqnarray*} \xi_1 = -\frac{1}{\sqrt{3}} &,& \eta_1 = -\frac{1}{\sqrt{3}} \\ \xi_2 = +\frac{1}{\sqrt{3}} &,& \eta_2 = -\frac{1}{\sqrt{3}} \\ \xi_3 = +\frac{1}{\sqrt{3}} &,& \eta_3 = +\frac{1}{\sqrt{3}} \\ \xi_4 = -\frac{1}{\sqrt{3}} &,& \eta_4 = +\frac{1}{\sqrt{3}} \end{eqnarray*} $$ Nel caso di elemento sottointegrato (1x1 punti di integrazione in $\xi$,$\eta$) ho $$ m=1 $$

$$ w_1=4 $$

$$ \begin{eqnarray*} \xi_1 = 0 &,& \eta_1 = 0 \end{eqnarray*} $$