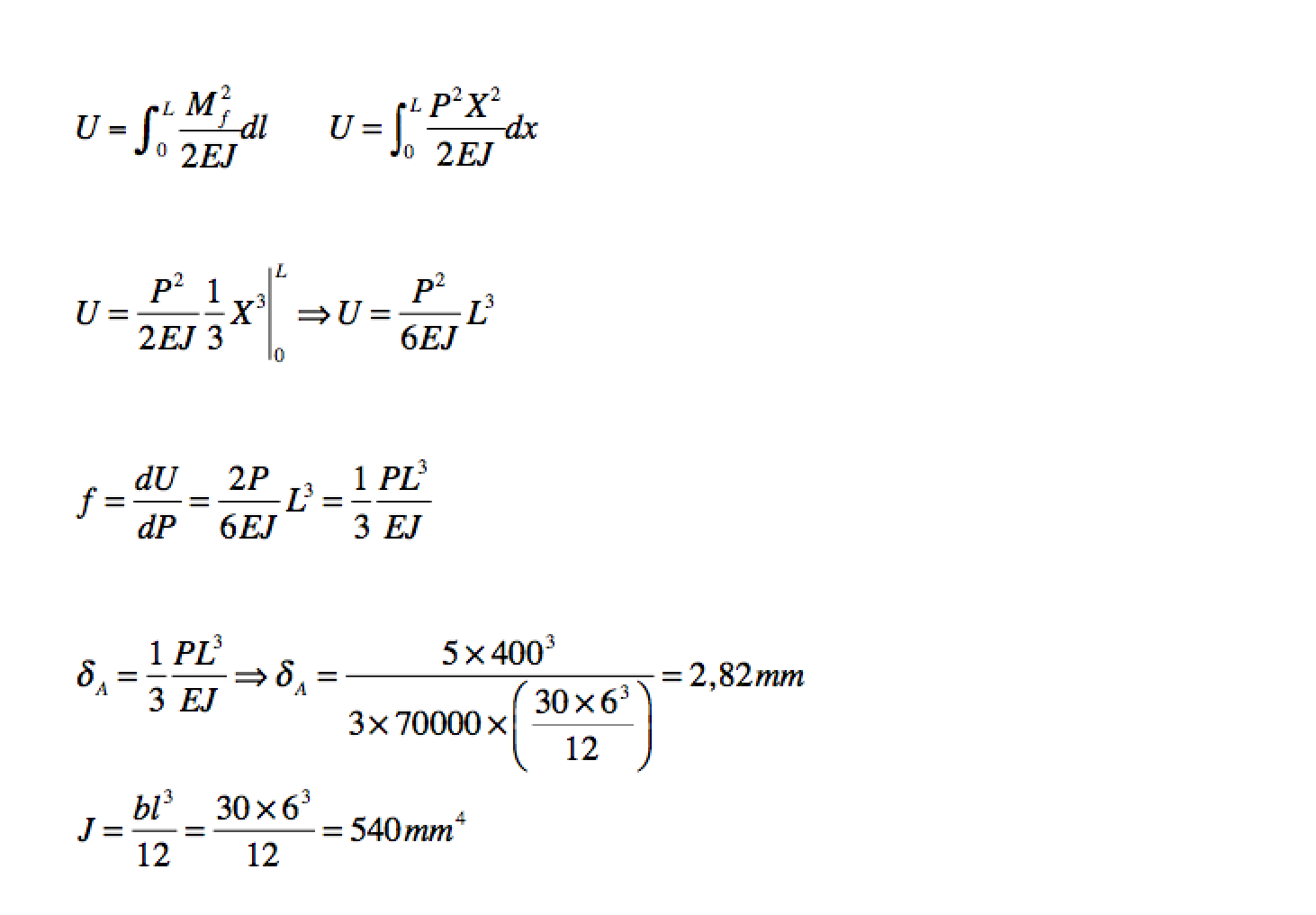In questa lezione vediamo la distorsione di un elemento isoparametrico e verifichiamo se il software riesce a risolvere il problema. (controllo che lo Jacobiano converta bene l'elemento finito)

Teoria della trave su Marc Mentat; modello della trave 2D.

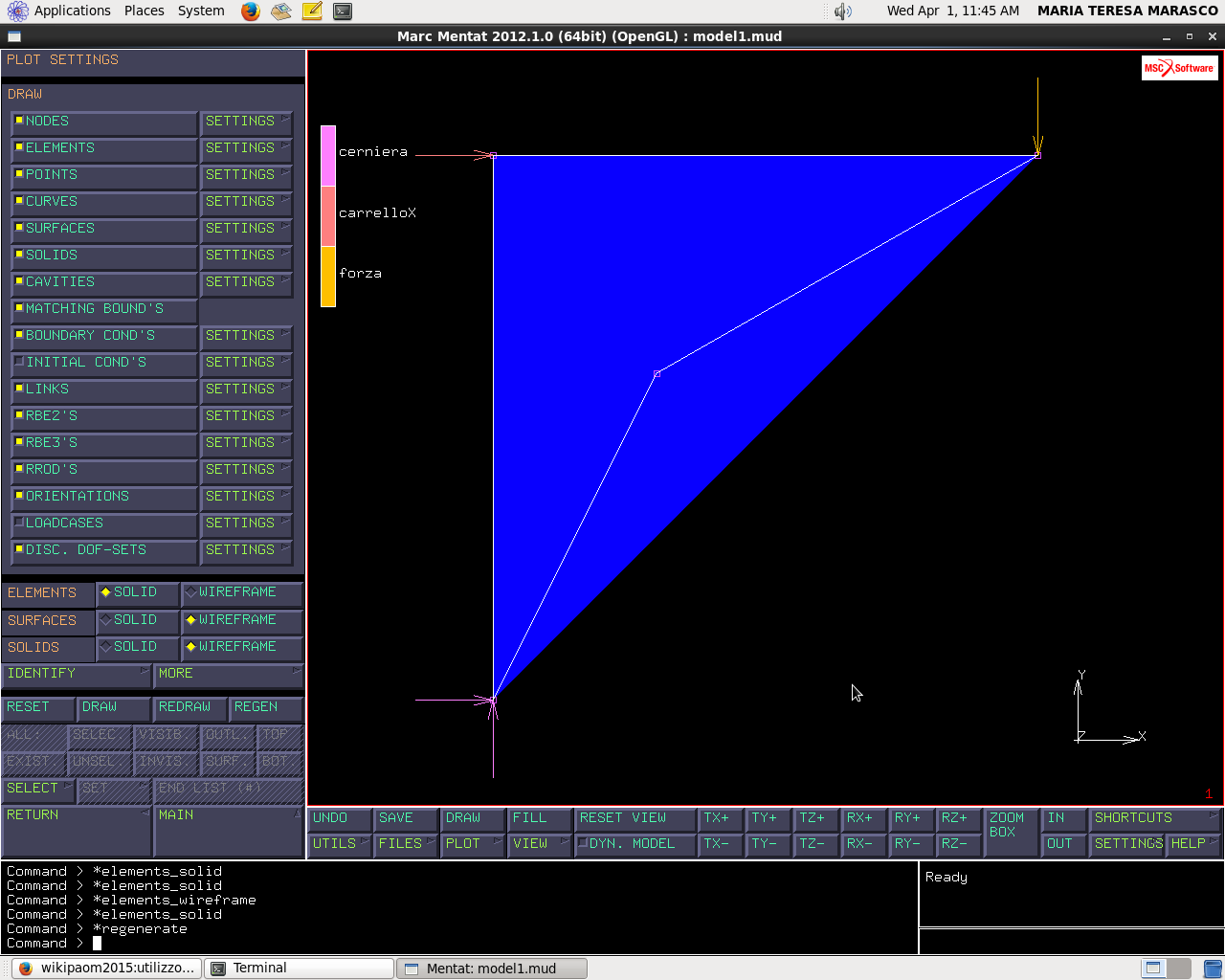
Realizzeremo in Marc un elemento quadrangolare e lo vincoliamo isostaticamente con una cerniera e un carrello.

Applicheremo un carico di 1N verticale sul nodo (1;1;0).

Inseriamo le coordinate dei nodi dell'elemento finito

Mesh generation → Nodes → add : (0;0;0), (0,3;0,6;0), (1;1;0), (0;1;0)

Controllo che su “Element class” sia attivo “Quad(4)”

Mesh generation → elements → add : seleziono i nodi in senso antiorario per avere circuitazione positiva.

Definiamo la natura dello stato tensionale (tensione piana)

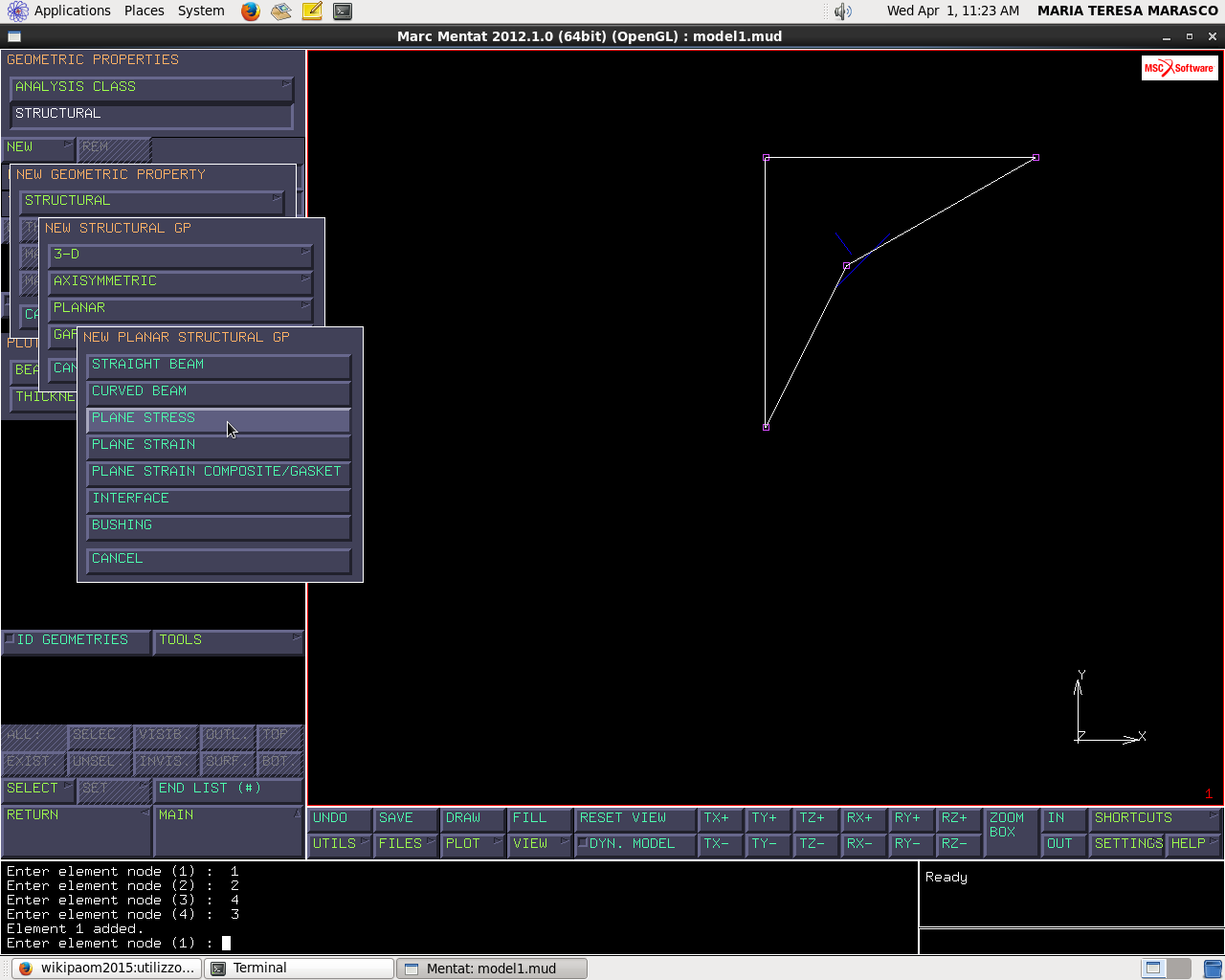
Geometric properties → new → structural → planar → plane stress

(Diamo il nome “tensione_piana”)

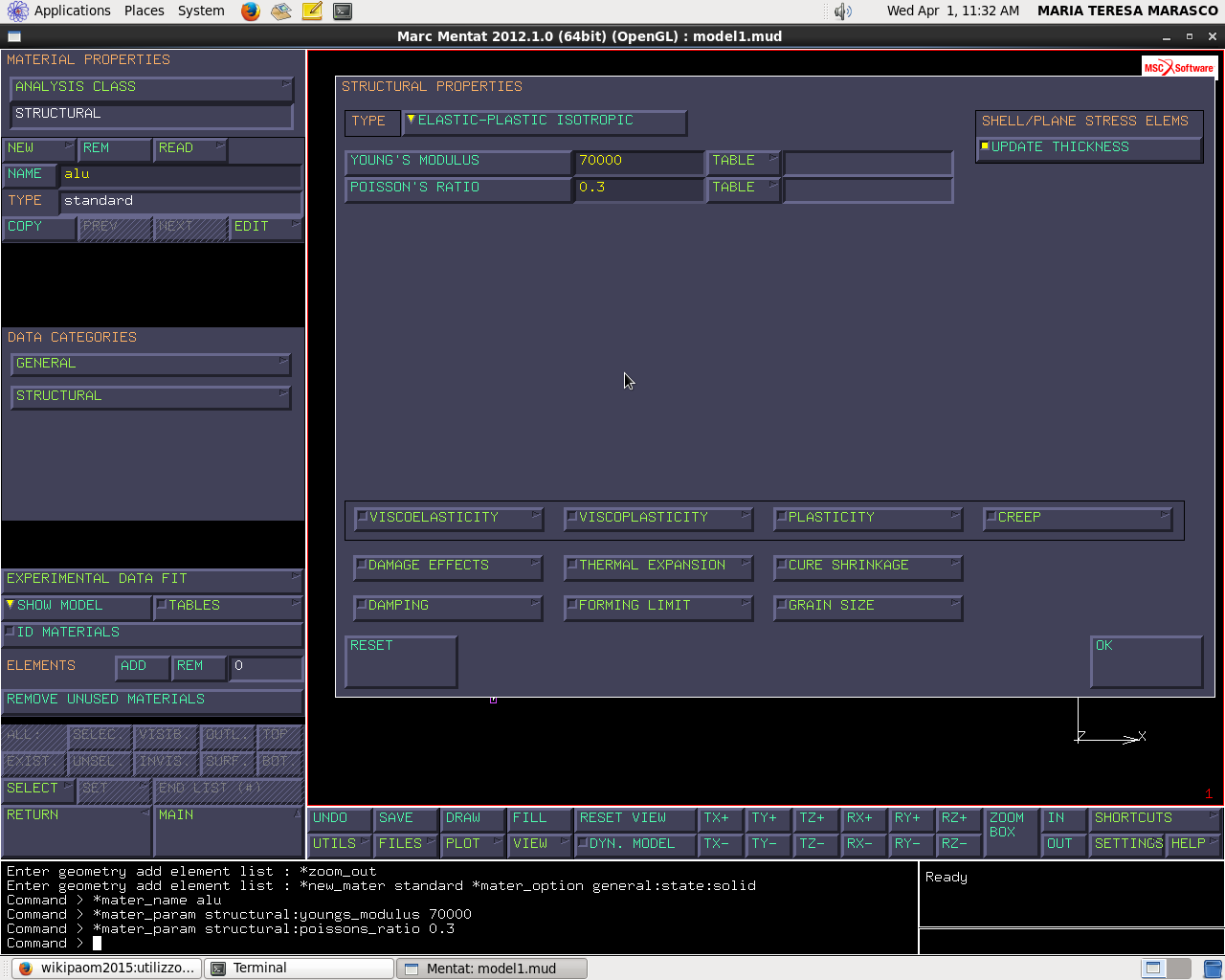
Definiamo il materiale

Material properties → material properties → new → standard → structural → (E = 70000 MPa Poisson ratio = 0.33 )

(Diamo il nome “Alu”)

N.B. ulteriori informazioni sui materiali sul sito http://www.matweb.com/index.aspx

Vincolamento e caricamento dell'elemento finito.

Cerniera

Boundary conditions → new → structural → fixed displacement → properties → (displacementX=0 displacementY=0) → nodes → add: (0;0;0)

(Diamo il nome “cerniera”)

Carrello

Boundary conditions → new → structural → fixed displacement → properties → (displacementX=0) → nodes → add: (0;1;0)

(Diamo il nome “carrelloX”)

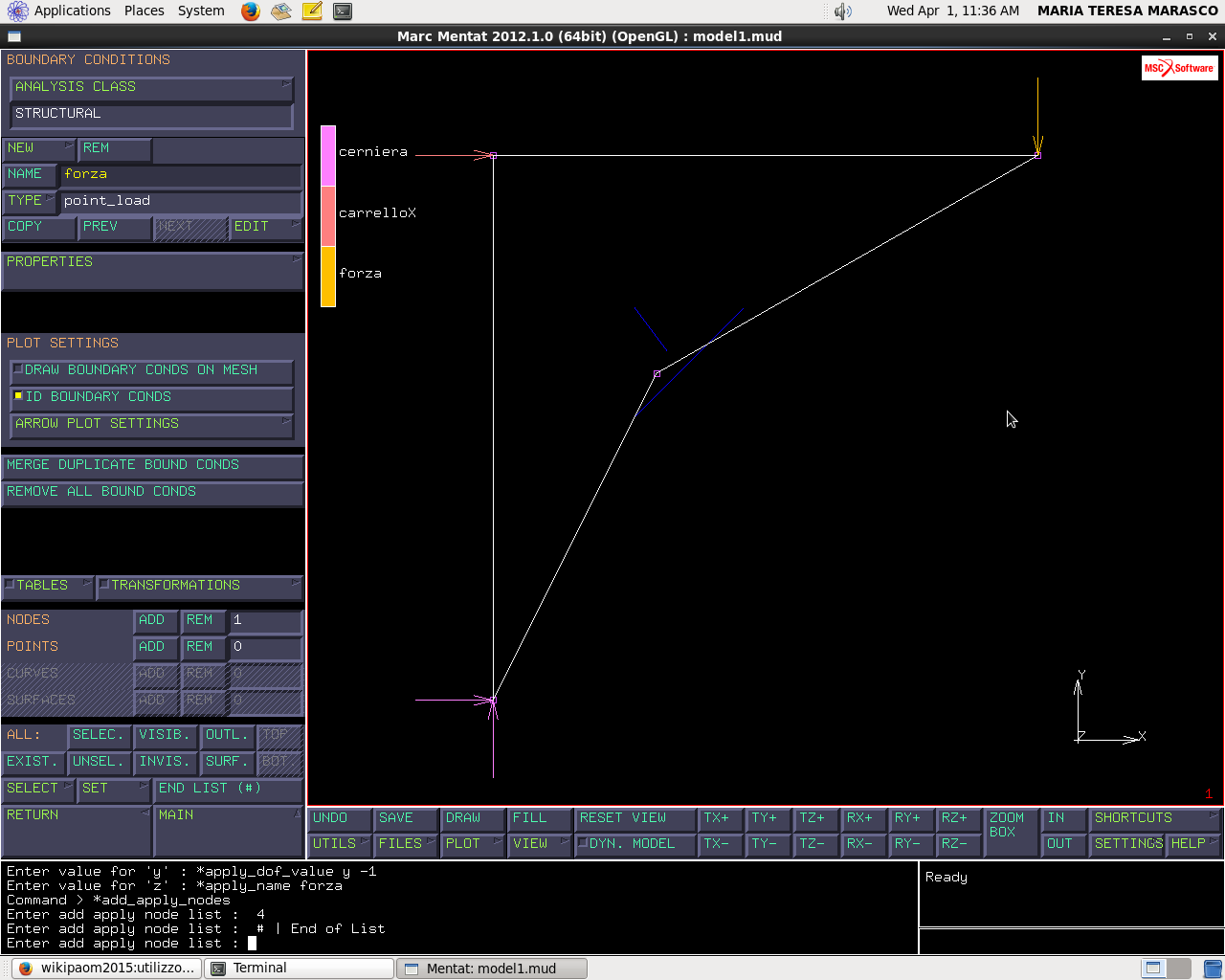
Forza

Boundary conditions → new → structural → point load → properties → (forceY=-1N) → nodes → add: (1;1;0)

(Diamo il nome “forza”)

Controllo della circuitazione dell'elemento

Mesh generation → check → upside-down (risulta nessun elemento invertito)

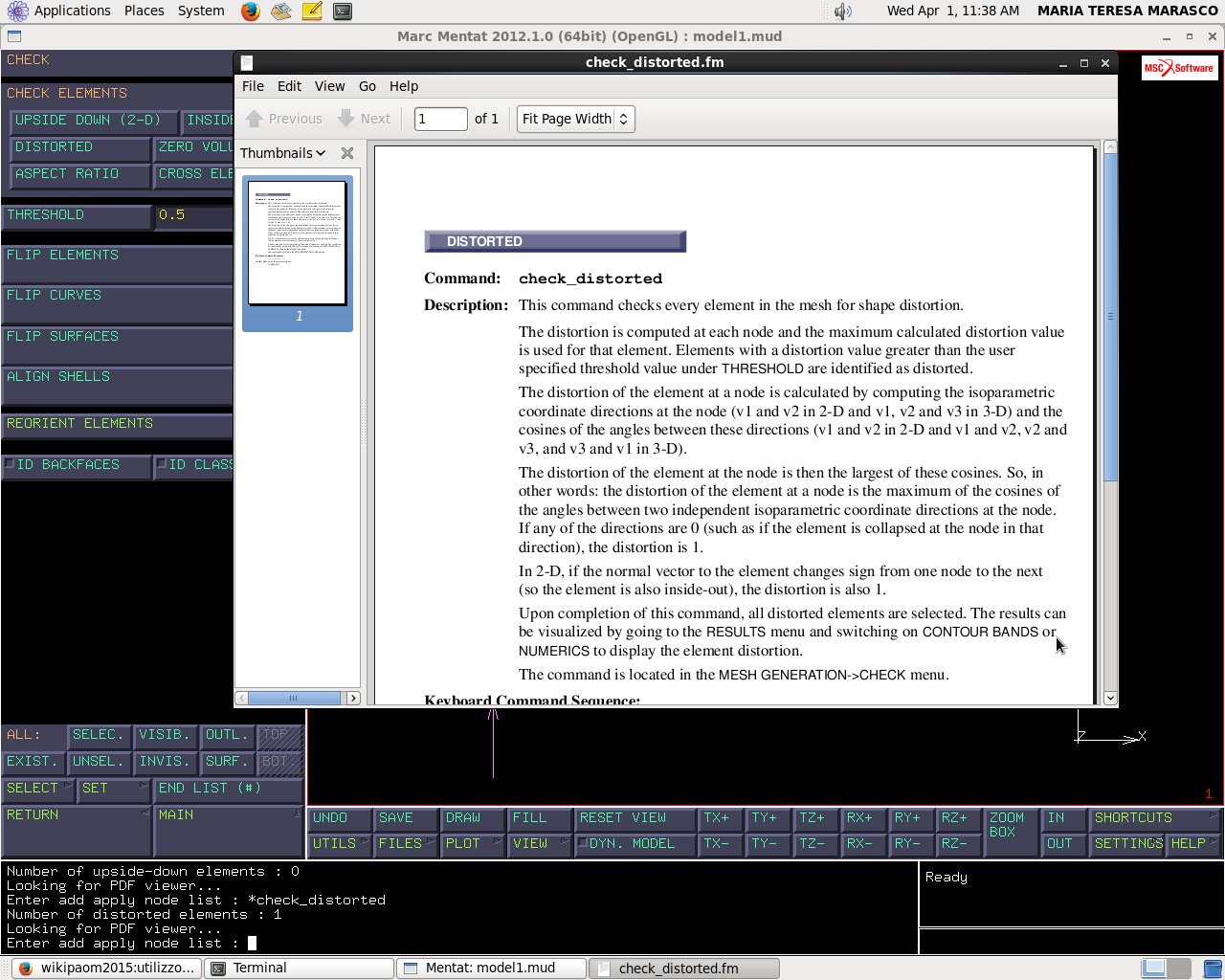
Controllo della distorsione dell'elemento (verifica della Jacobiano)

Mesh generation → check → distorted (risulta un elemento distorto)

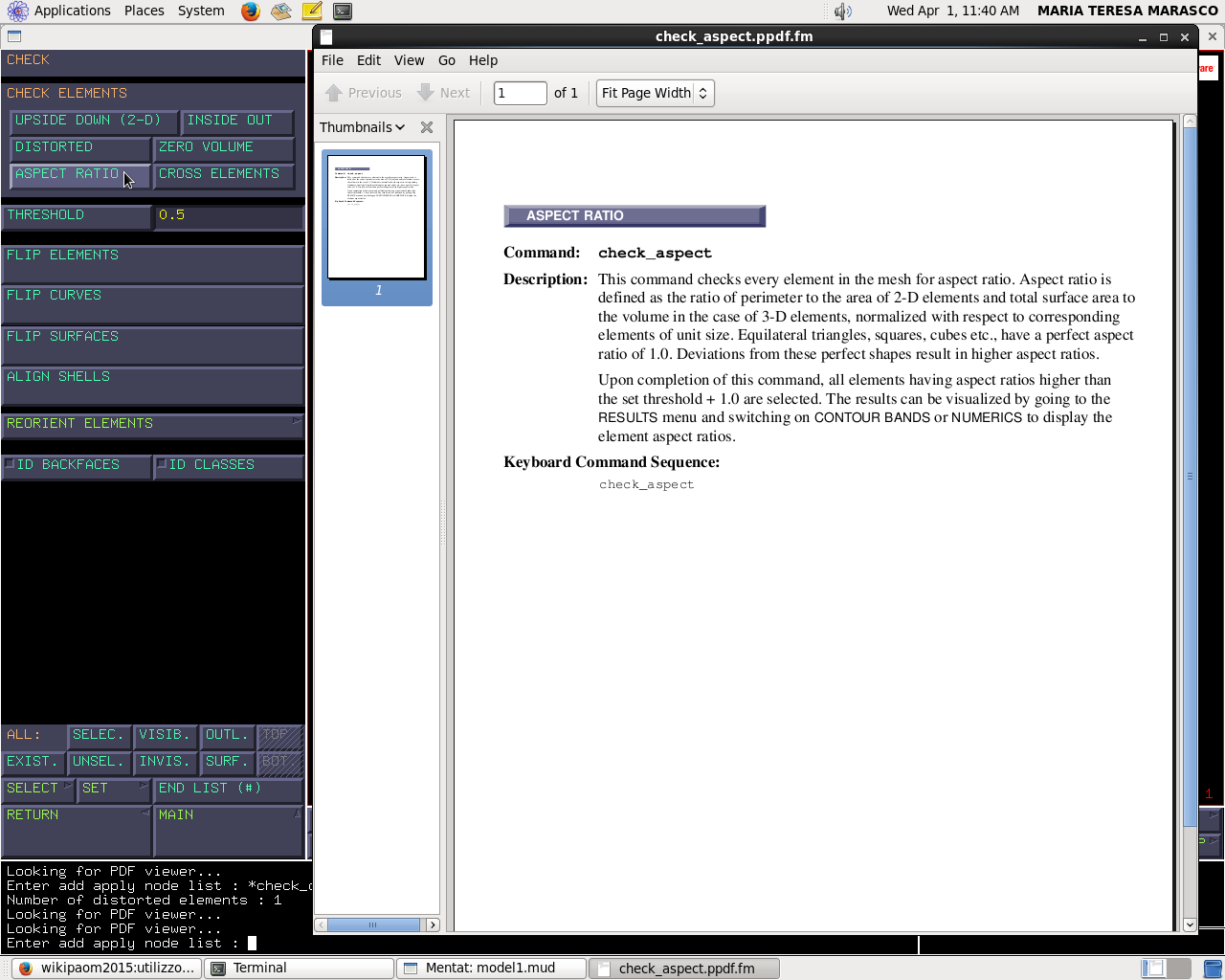
Controllo “aspect ratio”: quanto l'elemento è aghiforme.

Aspect ratio: rapporto perimetro-area.

Mesh generation → check → aspect ratio (risulta zero elementi aghiformi) (threshold=0.5)

Lanciamo la simulazione

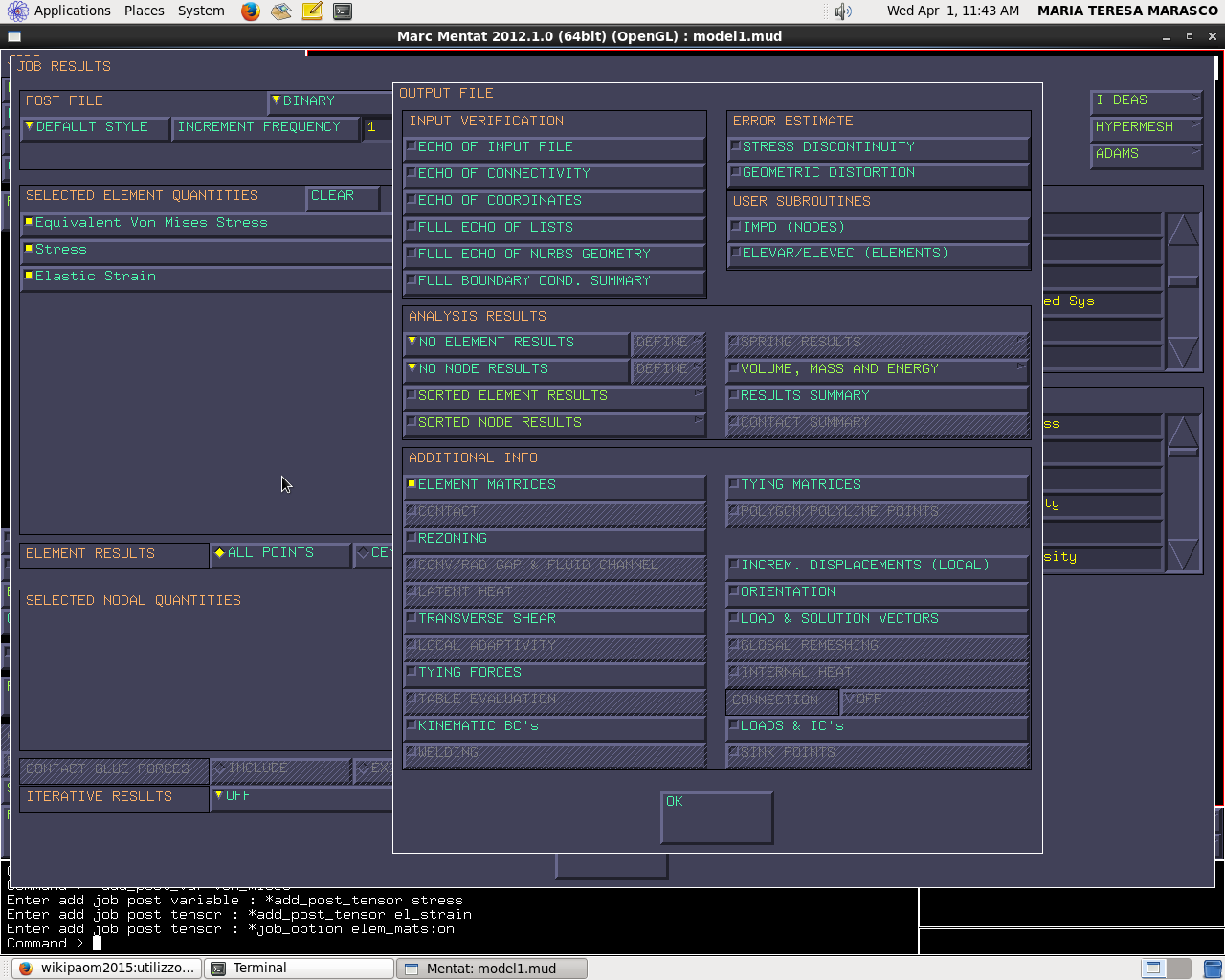
Jobs → new → structural → properties (facciamo attenzione che in “analysis dimension” sia selezionato “plane stress”) → job result → plane stress (seleziono: “stress”, “elastic strain”, “equivalent Von Mises stress”)

In “output file” seleziono “element matrices” (chiedo al solutore di inserire nel file di output le matrici di rigidezza degli elementi, così possiamo controllarle)

Run → submit → monitor

In “exit number” invece di 3004 (calcolo corretto), ottengo 13 (non riesce a trasformare l'elemento in isoparametrico).

Plot → solid element → regen

Fatto ciò possiamo tramite il manipolatore Maxima ricavare lo Jacobiano dell'elemento finito analizzato.

Analizziamo ora l'elemento trave e confrontiamo la soluzione ottenuta tramite il software con la soluzione analitica (teorema di Castigliano).

Teorema di Castigliano: In un sistema elastico, la derivata parziale dell'energia totale elastica rispetto ad una forza (o coppia) definisce lo spostamento (o rotazione) del punto di applicazione nella direzione di applicazione della forza (o coppia).

Materiale: alluminio

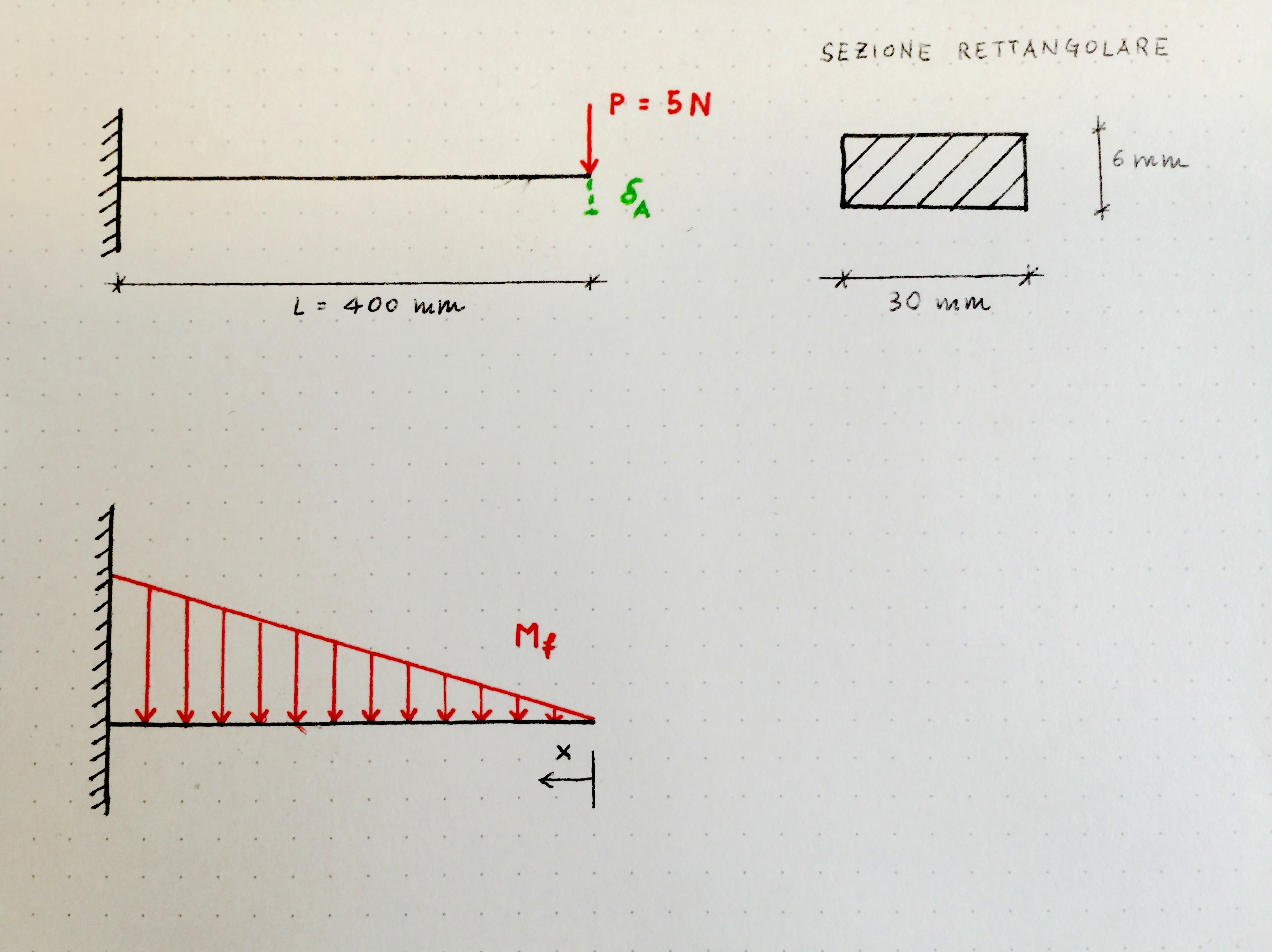
Carico: P=5N

Lunghezza: L=400mm

Sezione rettangolare b * l = 30mm * 6mm

Verifichiamo il risultato in Mentat

Realizziamo l'elemento trave

Mesh generation → nodes → add: (400;0;0),(0;0;0).

Controllo che su “Element class” sia attivo “Line(2)”

Mesh generation → elements → add : seleziono i nodi

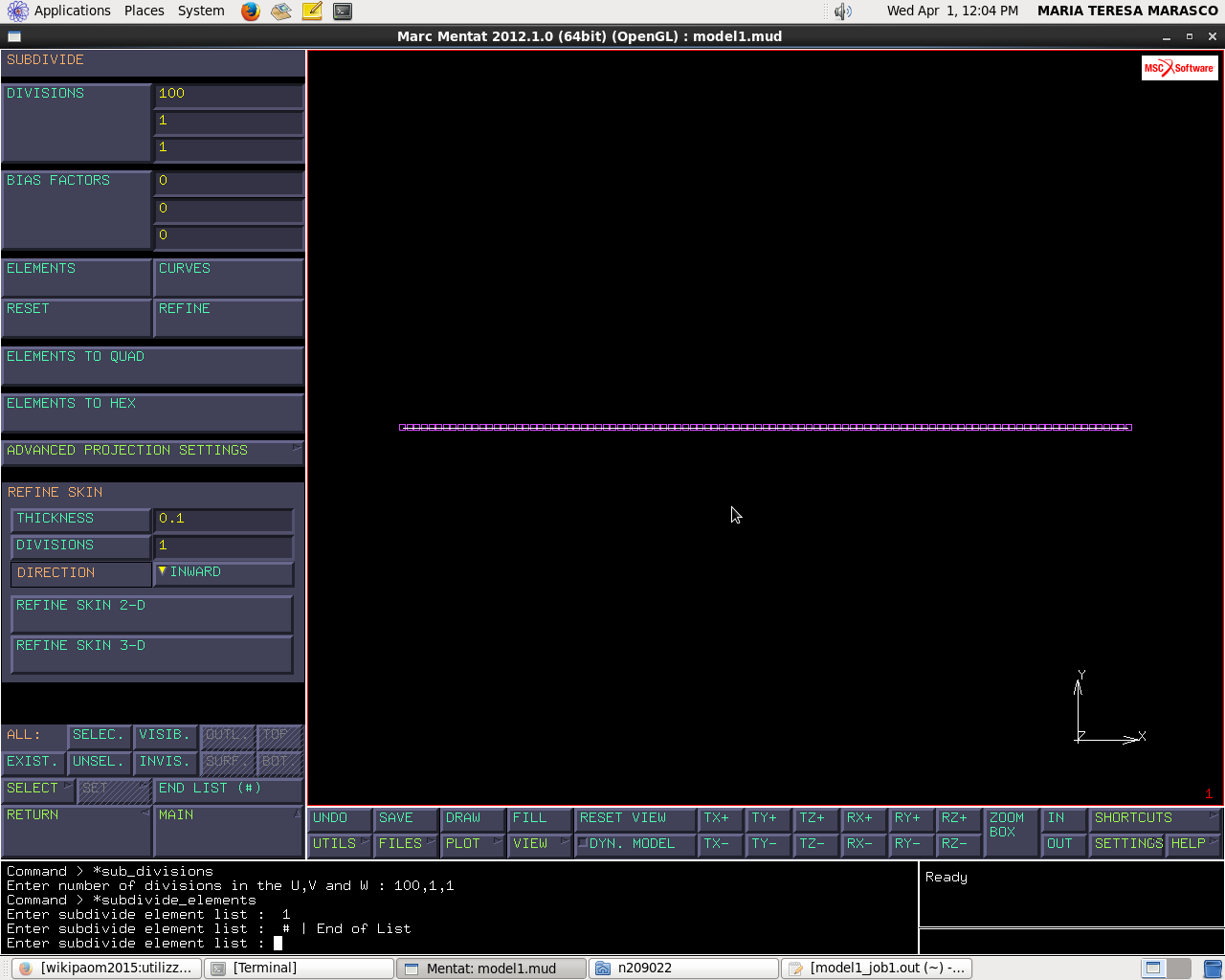
Subdivide → divisions (100,1,1) bias factor (1,1,1)

Mesh generation → sweep → sweep all risulta una cancellazione di due nodi agli estremi.

Con gli elementi shell dobbiamo fare attenzione alle proprietà geometriche.

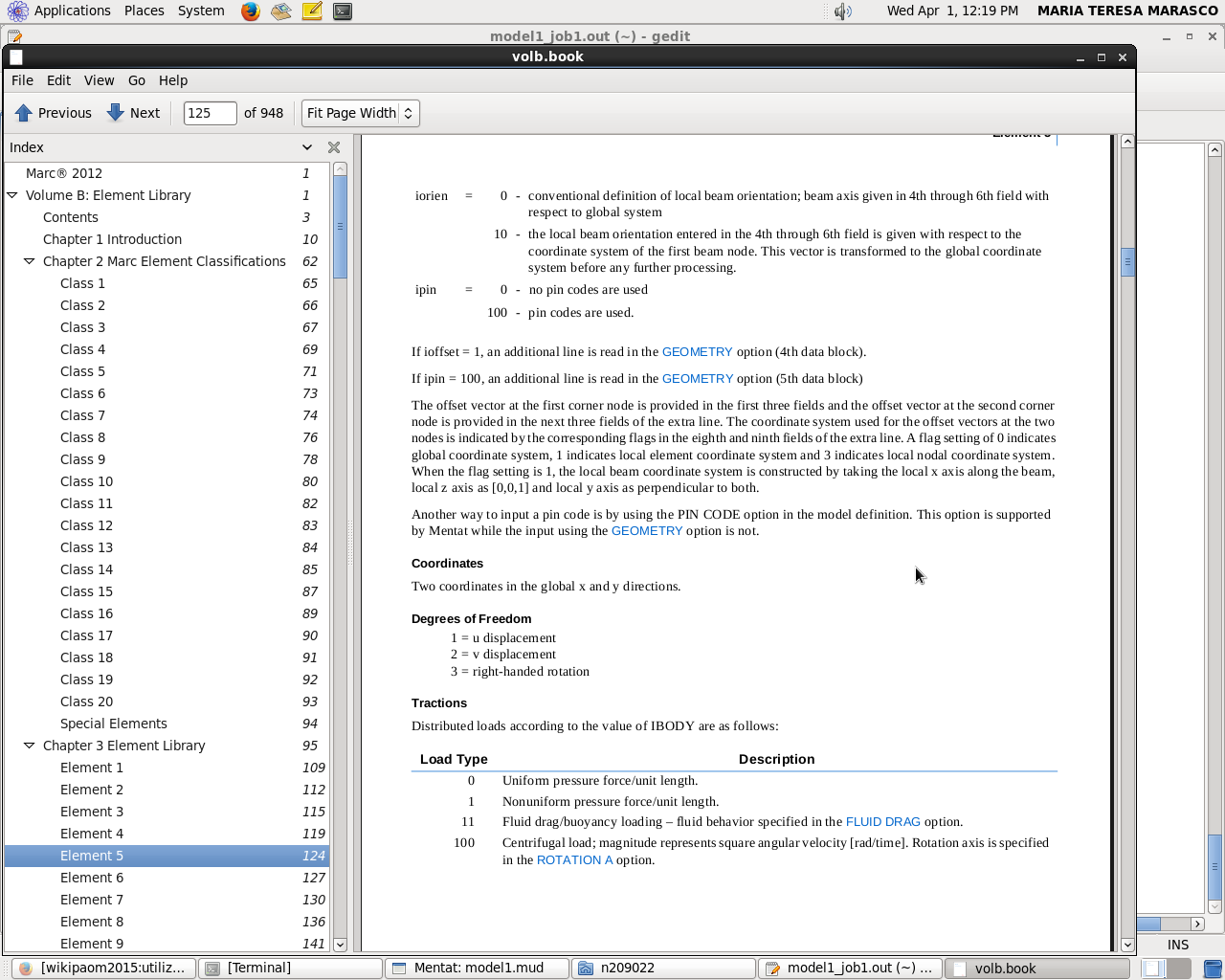
In questo caso non è soltanto planar ma va selezionato “straight beam” per rappresentare la teoria della trave dritta (nel software l'elemento è “element5”).

Ogni nodo della trave ha 3 DOF: traslazioni in x e y, rotazione in z.

Teoricamente potrei dare un incastro. (nel Tria(3) non potevo)

Dimensioni della matrice di rigidezza 3*n X 3*n (con n numero di nodi = 101, 3 rappresenta il numero di DOF).

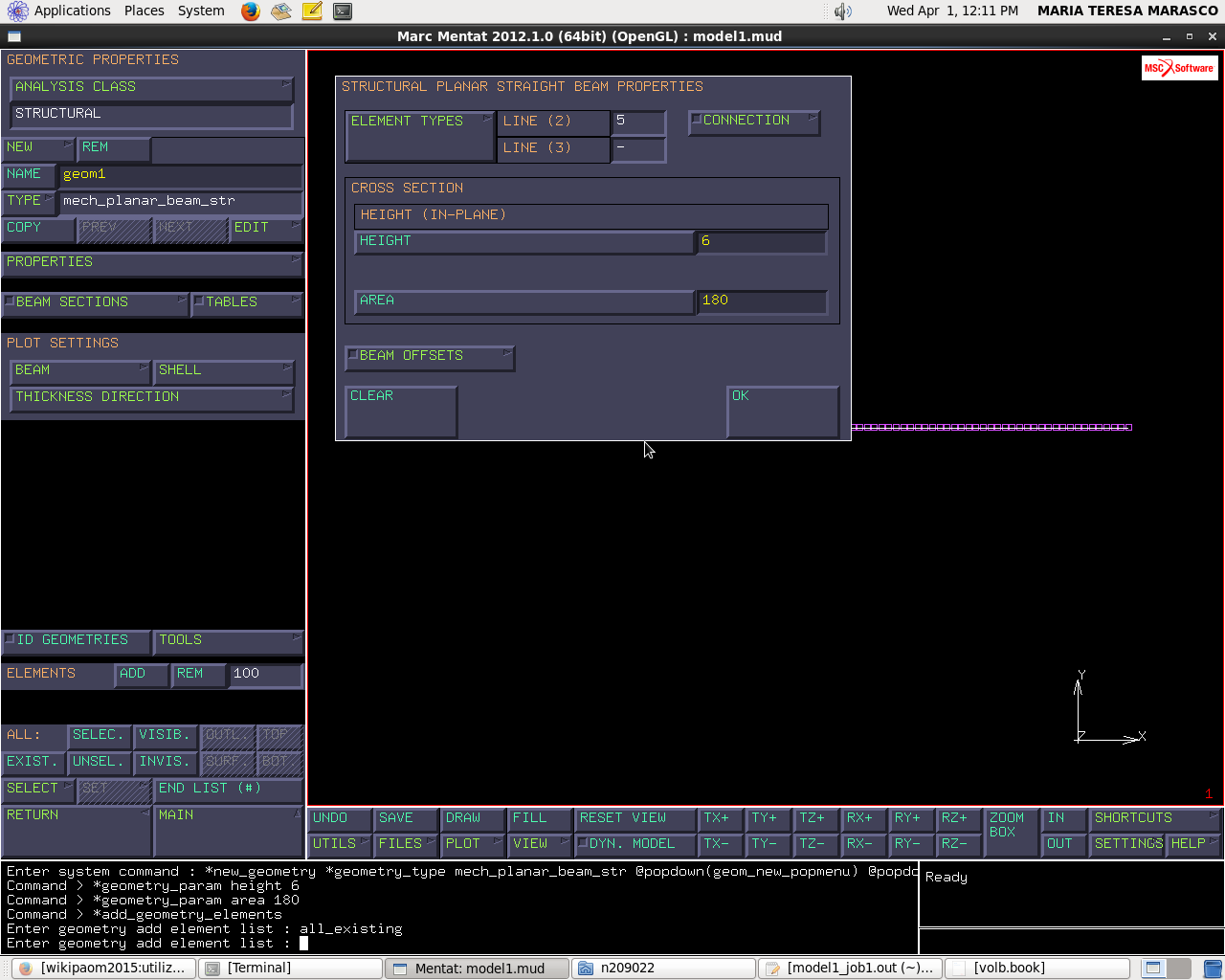
Definiamo le dimensioni della sezione.

Il programma richiede altezza e area.

Geometrical properties → new → structural → planar → straight beam → properties (inserisco altezza e area)

Materiale: alluminio (alu)

Material properties → material properties → new → standard → structural → (E = 70000 MPa Poisson ratio = 0.33 )

Vincolamento e caricamento della trave

Incastro

Boundary conditions → new → structural → fixed displacement → properties → (displacementX=0 displacementY=0 displacementZ=0) → nodes → add: (0;0;0)

N.B. Per bloccare la rotazione in Z seleziono “displacementZ” al posto di “rotationZ” in quanto avrei una deformata sbagliata a causa di un errore interno al software.

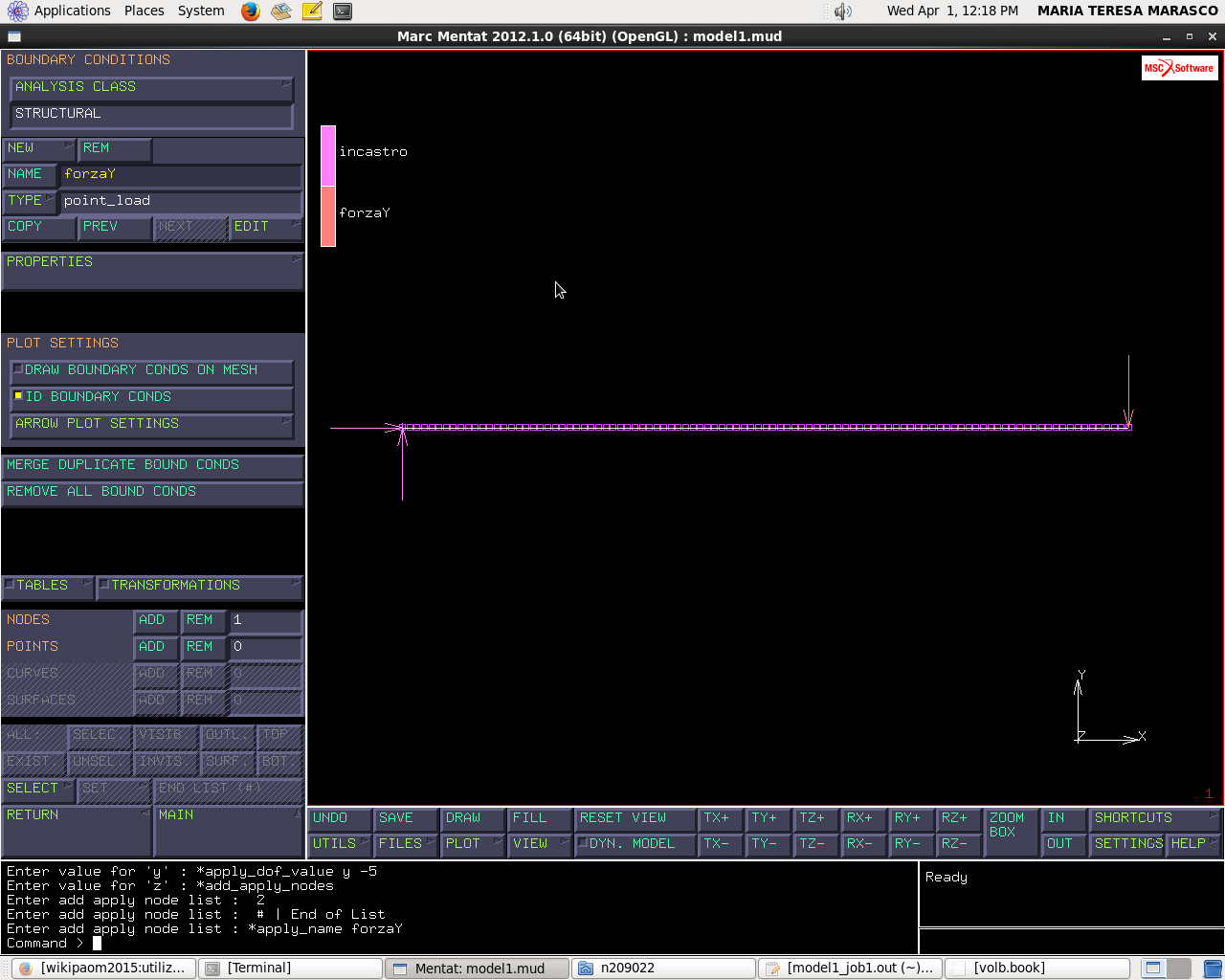
Forza

Boundary conditions → new → structural → point load → properties → (forceY=-5N) → nodes → add: (400;0;0)

(Diamo il nome “forzaY”)

Lancio la simulazione

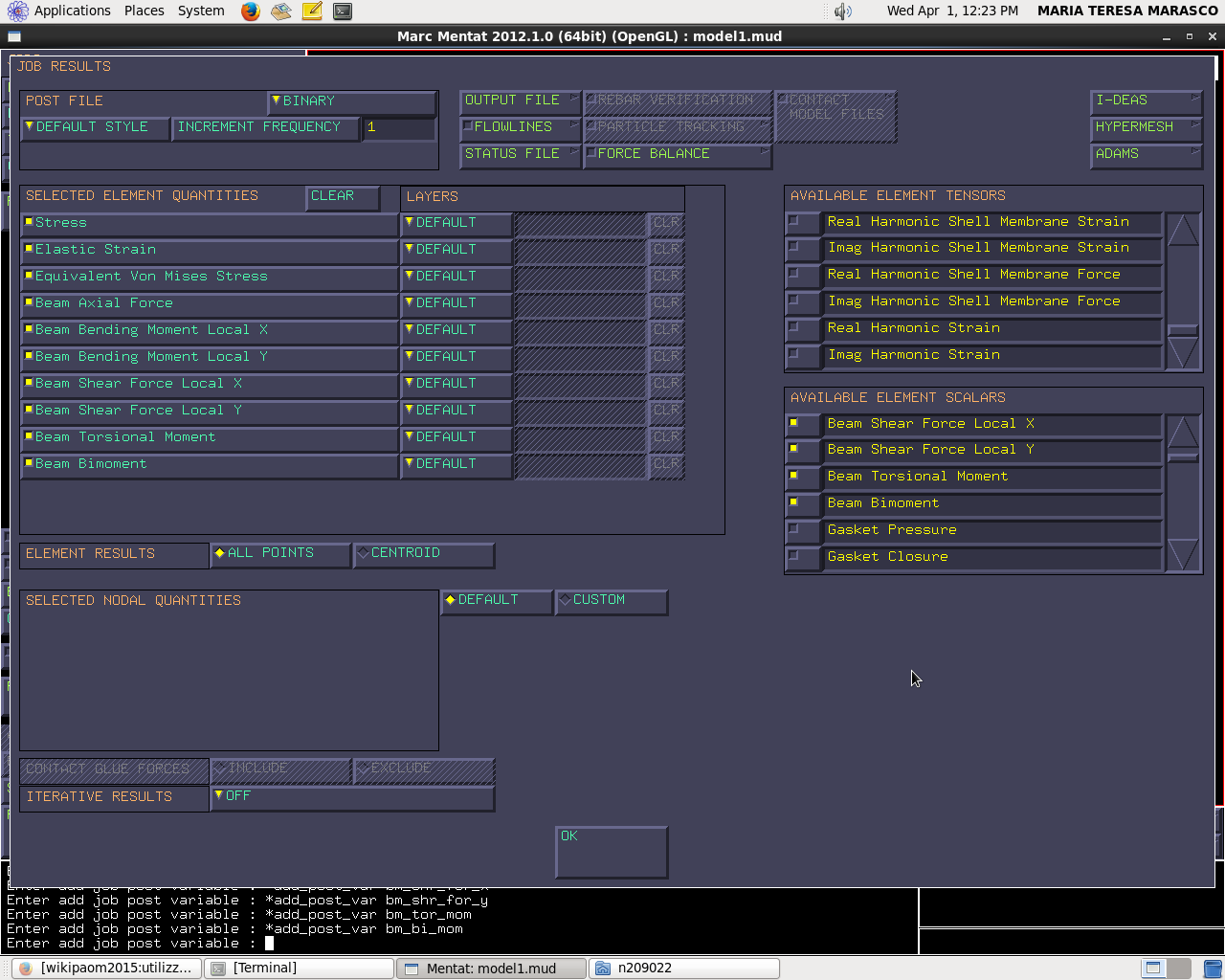
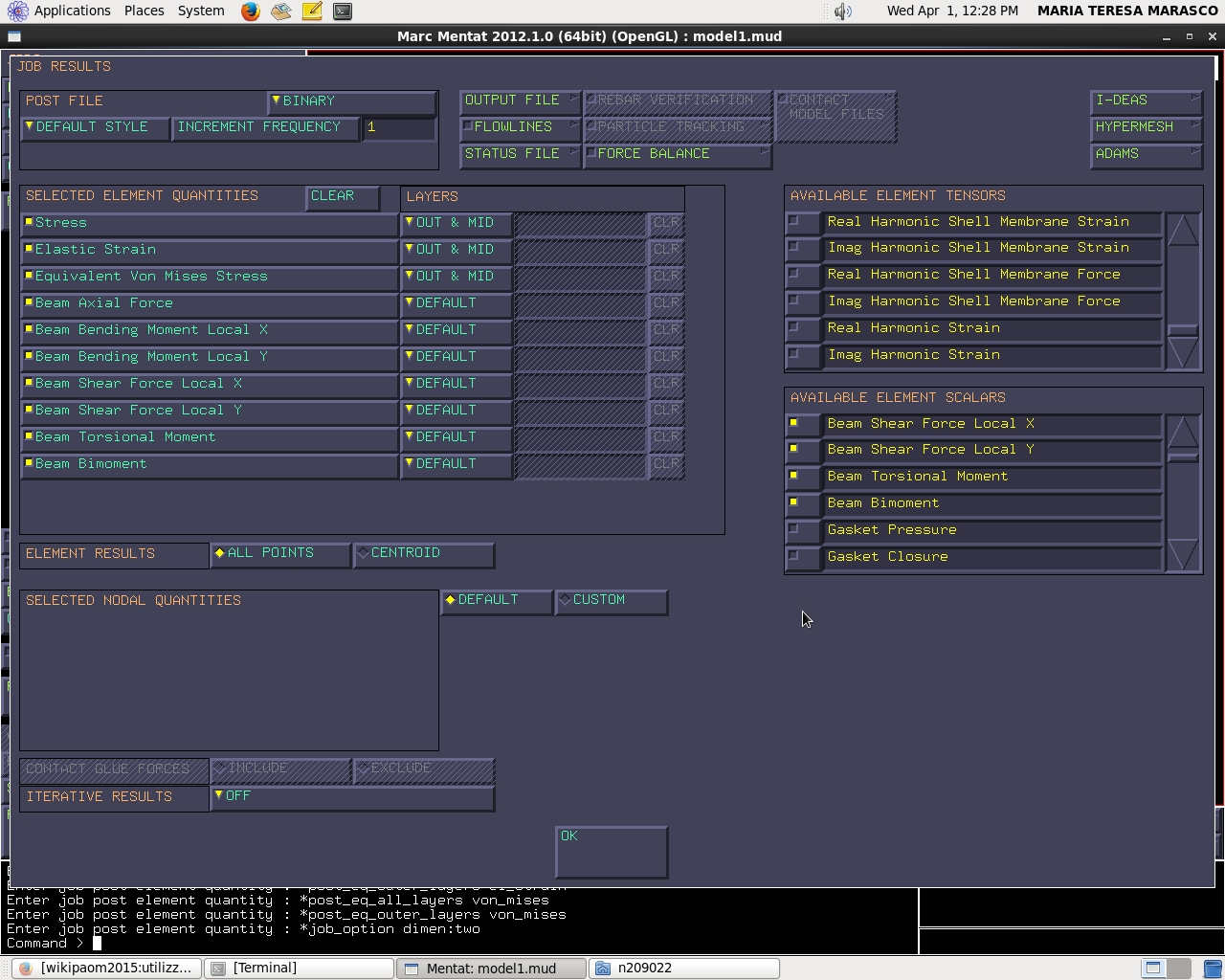
Jobs → new → structural → properties (facciamo attenzione che in “analysis dimension” sia selezionato “2D”) → job result → plane stress (seleziono: “stress”, “elastic strain”, “equivalent Von Mises stress”, “Beam axial force”, “Beam bending xy”, “Beam shear xy”, “Beam torsional”, “Beam bimoment”)

Accanto a “Stress” c'è selezionato “default”; seleziono “out & mid” in quanto indago lo stato tensione agli estremi e sull'asse neutro.

Lo applico solo allo stato tensionale essendo indifferente per gli altri parametri.

Renumber-all: rende bandata la matrice di rigidezza.

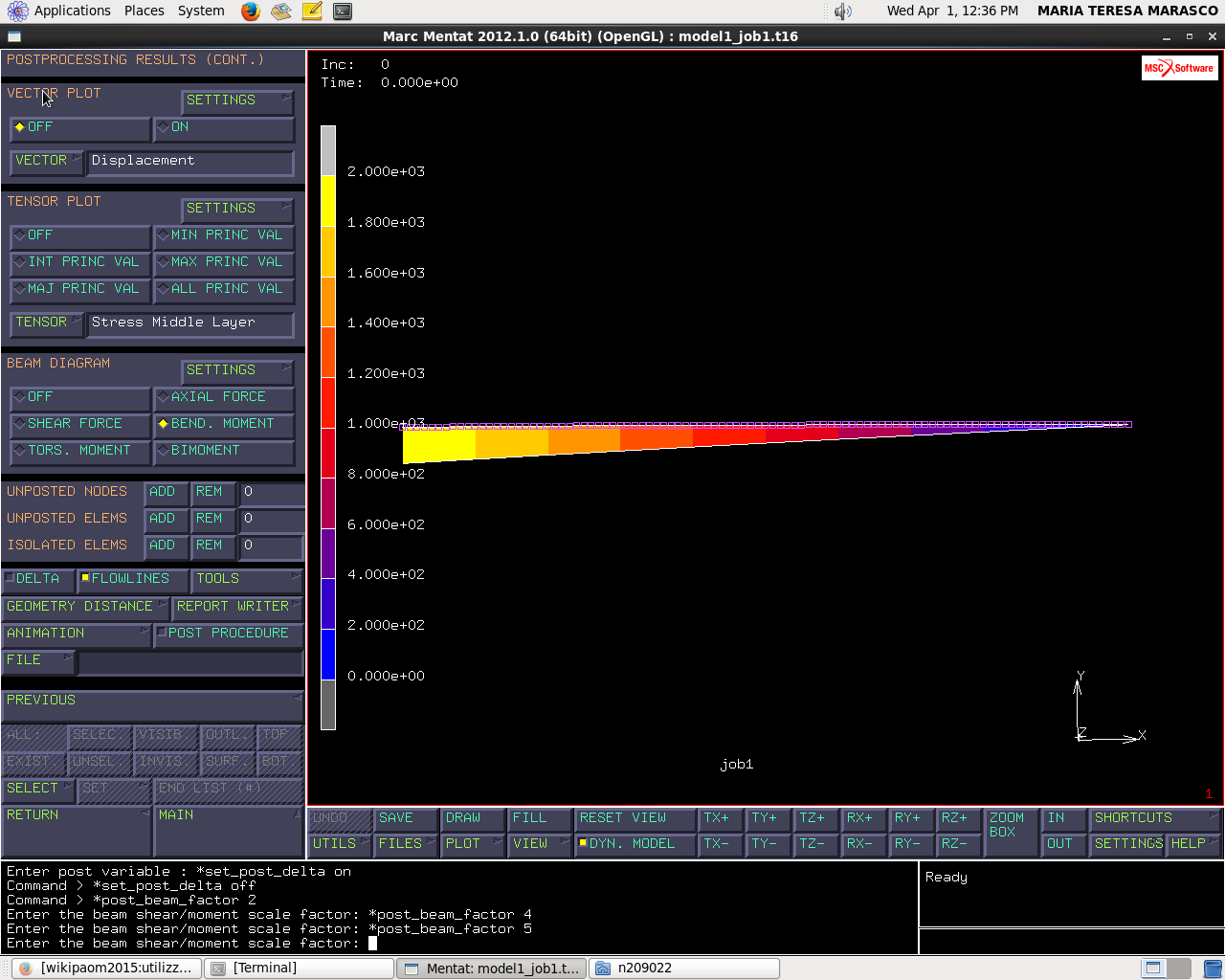
Run → submit → monitor → open post file → more → maximum principal value stress → on

I valori numerici calcolati dal software (anche la deformata della trave all'estremità libera) corrispondono ai valori calcolati con la teoria di Castigliano con le formule sopra riportate.