modello fine lezione scorsa, gruppo b

foglio di calcolo risposta e inertanze

risposta spost. y impronta a terra ant. dx a forza unitaria ivi applicata, range 1-100Hz, passo 0.5Hz

piramide_buckling_base_v000.mfd

Struttura di esempio:

• struttura tubolare a schema piramidale.
  • base 600×750 mm
  • altezza 600 mm
• sezioni tubolari con diametro esterno 12mm, spessore di parete 2 mm; quindi piuttosto snelle.
• alluminio 6060 T6, E=70000 MPA, ys~Rp02=165 MPa
• giunzioni modellate per collasso nodale - continuità di rotazioni e spostamenti.
• appoggiata sui quattro vertici della base, con posizionamento isostatico.
• caricata da un carico verticale di 1000N compressivo applicato al vertice della struttura.

Note sul modello specifico:

• si inseriscono tra i risultati le caratteristiche di sollecitazione su trave “beam orientation vector”, “beam axial force”,…
• la sezione ha (vedi guida elemento) 16 punti di integrazione sulla circonferenza (layers); richiedere in output una “equivalent von Mises stress” con opzione “max & min” sui layer per verificare lo stato tensionale del materiale.
• si rileva un fattore di amplificazione del carico applicato (1000N) a criticità di 8.462
• si rileva un abbassamento del punto di applicazione della forza a 1000N di 0.07020mm

Il sistema è in equilibrio tuttavia non è posizionato nello spazio, quindi sono stati aggiunti i seguenti vincoli di posizionamento:

• due vincoli di posizionamento in direzione x (un carrello in direzione x ed un carrello in direzione y che bloccano le traslazioni in x e la rotazione z).
• un vincolo di posizionamento in direzione y sul nodo centrale.

La struttura ha due piani di simmetria (xz e yz), quindi le deformate sono simmetriche a meno di un moto di corpo rigido non generalmente simmetrico.

La sezione ha area 62.84mm^2 e snervamento compressivo sotto sforzo normale di 10367 N.

Notare che su uno dei montanti è possibile preimpostare una perturbazione della rettilineità di entità 1mm.

piramide_buckling_rinforzotiranti_v000.mfd

piramide_buckling_rinforzopannelli_v000.mfd

instabilità travi perturbate; l=1000 mm, sezione circolare rm=10mm, spessore di parete 1mm, acciaio.

link al file di interesse: modello fine lezione scorsa, gruppo b

Questo modello della monoscocca rispetto al precedente presenta delle variazioni: il baricentro del gruppo ruota non coincide con quello del parallelepipedo che lo rappresenta (centro ruota), questo perché non è necessaria la coincidenza tra i due per i calcoli di dinamica veicolo. Il carico dinamico applicato è in direzione y anziché z e sulla ruota anteriore destra, corrispondete ad una rapida sollecitazione laterale come ad esempio una rapida sterzatura improvvisa. Il carico è applicato al centro dell’impronta a terra dello pneumatico (collegato al centro ruota con RBE2) perciò quel punto è nodo dipendente quindi può essere caricato ma non vincolato. Il carico non è puntualmente equilibrato, se non da forze inerziali.

Lanciando il calcolo in due step si ottiene il disequilibrio della struttura in un primo momento e nel secondo aggiunge ai carichi esterni una equilibrante di tipo inerziale e risolve la struttura.

L’obiettivo dell’analisi è trovare l’accelerazione sul g.d.l. caricato quindi in questo caso in direzione y del nodo centro impronta ruota anteriore dx, per cui si pone una piccola massa a terra su cui il programma calcola le forze inerziale, dividendo per la massa si ottiene l’accelerazione e l’inertanza su quel grado di liberà a carico statico unitario. Dovrebbe essere la stessa anche a carichi dinamici a basse frequenze compatibilmente con l’errore che vogliamo.

Problema dinamico:

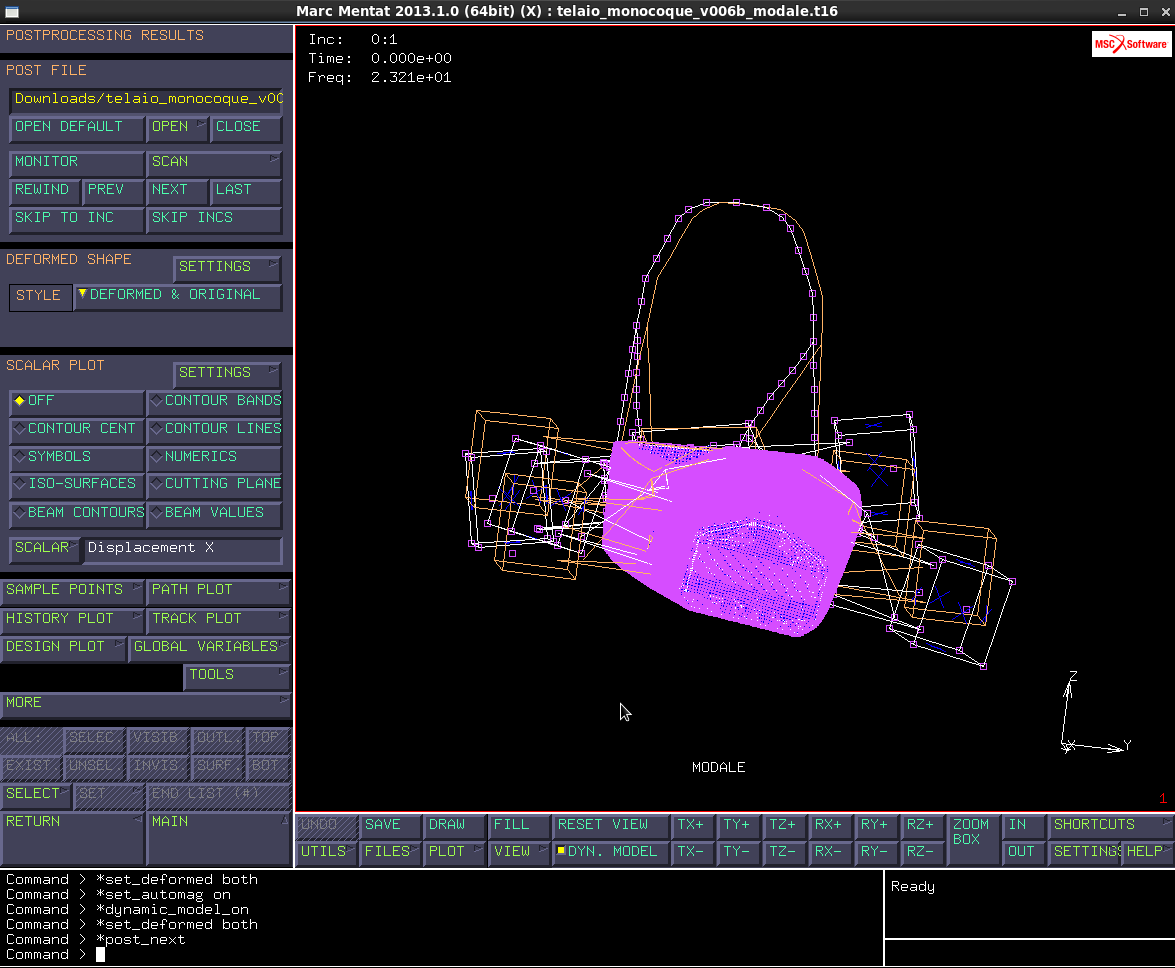
Estrazione dei modi propri e frequenze proprio con telaio libero nello spazio:

*Main → loadcases → new → dynamic modal

Cosi si trovano i moti propri della struttura, ma non essendo vincolata i primi sei modi sono quelli di corpo rigido a frequenza nulla, il Lanczos potrebbe dare errore, senza entra nel dettaglio si procede definendo le proprietà:

*Properties → low frequency: 1Hz (cosi si evita di considerare i moti di corpo rigido)

• →guardare comando (seleziono i primi 10 modi propri)

Cliccare su * non definite positive , per avvertire il solutore che la struttura è svincolata, risulterà labile. Ad 1Hz l’oscillazione è troppo lenta per essere di interesse telaistico.

Creare il Job:

*→Main→job→new→strutural→name: modale

• →proprieties→ initial load→ lasciare attiva solo la massa di campionamento (1mg);

• →selezionare il loadcase creato in precedenza→ Run→ submit→ Open post file results→next.

Dai risultati si possono definire i range di frequenza per cui il modello statico approssima bene il calcolo, ossia almeno una decade sotto la frequenza del primo modo proprio che risulta essere 23,21 Hz. Tutte le sollecitazioni modulate con f minore di (23,21/2) Hz potranno essere trattate come quasi statiche.

Sempre dal file dei risultati, cliccare su: *→deformed&original

• →Deformed shape →Settings→automatic.

Cosi si vede la macchina deformata torsionalmente.

Cliccando su *→next si può osservare il secondo modo proprio del sistema a 49,51Hz Osservando un moto di sterzata, dovuto all’evidente deformabilità del meccanismo di sterzo.

*Plot→nodes→rem→regen

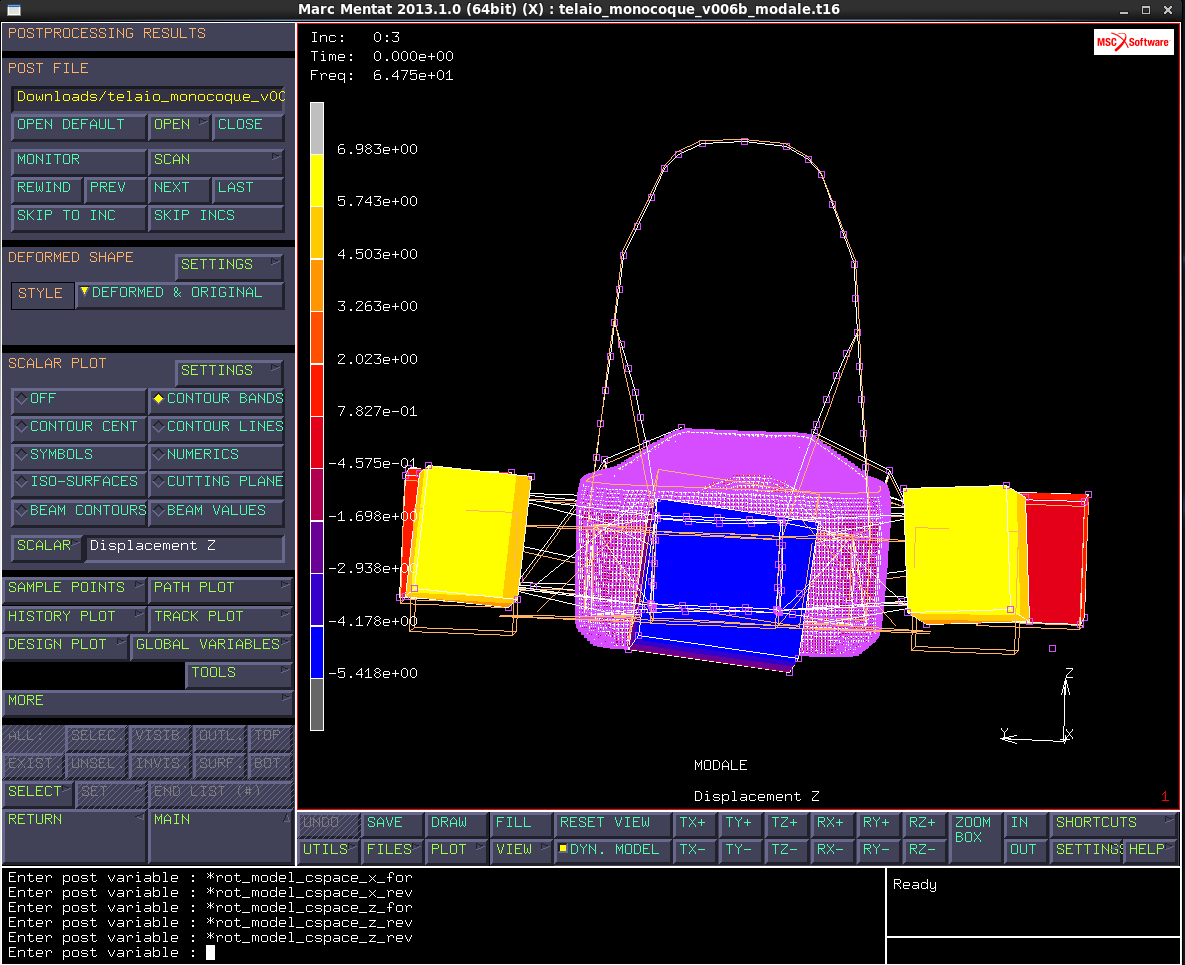
Dal file dei risultati scalar *→displacement z →contour bands

Si osserva che la piastra inferiore del monoscocca, a cui sono collegati i puntoni dello sterzo, deforma ad ‘’S’’ in maniera sensibile. Si potrebbe ovviare al problema rinforzando i punti di attacco dei puntoni dello sterzo oppure distanziandoli per irrigidire l incastro complessivo.

Il terzo modo proprio si ha a 64,75 Hz e si nota al posteriore che comincia ad oscillare; andando avanti i successivi modi proprio coinvolgono il motore per cui è necessario rafforzare gli attacchi motore al telaio per non farlo oscillare.

Cosa succede se applico una forza pulsante di 1N alla frequenza del primo modo proprio? La risposta dovrebbe essere non limitata, cedevolezza e inertanza infinite e rigidezza nulla. Lancio un calcolo di risposta in frequenza nell’ interno del primo modo proprio da 21 Hz a 25Hz campionando ogni 0,25 Hz (scegliendo un intorno stretto poiché il calcolo è troppo pesante). Prima di procedere assicurarsi di aver chiuso il file dei risultati del modello precedente tramite close. *Main→loadases →new →dynamic harmonic→ risposta prima risonanza risposta spost. y impronta a terra ant. dx a forza unitaria ivi applicata, range 1-100Hz, passo 0.5Hz

• → Proprierties →lowest frequency: 21

• → highest frequency: 25

• → #frequency: 20

• → load: disattivo i tre incastri presenti

Poiché tra le opzioni non è presente il point load static creato in precedenza che tra l’altro è inservibile per un’analisi in frequenza si crea un’apposita boundary condition:

*Boundary conditions→new→structural→harmonic point load→ name: carico 1N in direzione Y armonico

*Proprierties→ force y→ magnitude:1

• →phase: 0

*Plot→nodes→add→regen e togliendo il Dynamic model si seleziona il nodo dell’impronta a terra della ruota ant sx.

*Loadcases→proprierties→ load→attivo il carico 1N in direzione Y armonico, creato in precedenza.

*Job→copy (quello modale) →name: risposta prima risonanza

*Proprierties→ initial loads.

Si deseleziona l’analisi modale tranne la massa concentrata,selezionare loadcases creato in precedenza, ora avremo un initial load scarico con le masse concentrate campione, e a seguito di questo step 0 non vincolato procedo con analisi di risposta in frequenza in cui si modula la forza di 1 N da 21 a 25 Hz*→ Submit e attendere all’ incirca 6 minuti.

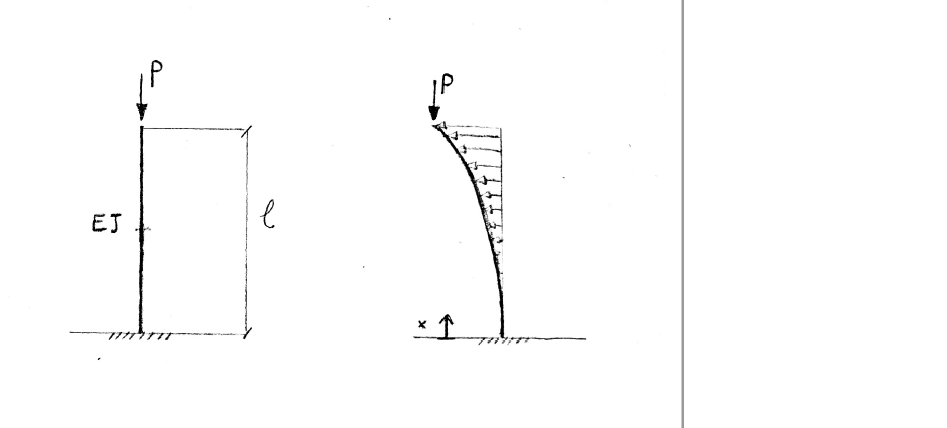
Data la seguente struttura di lunghezza l e di area della sezione sufficientemente piccola da sapere che snerva per instabilità elastica piuttosto che per compressione.

L’inflessione non è prevista da un calcolo lineare elastico che vedrebbe una colonna in compressione e la soluzione elastica è unica.

Di rigidezza flessionale EJ caricata con carico verticale compressivo P che non cambia direzione anche se la struttura si deforma per inflessione.

Considero l’equilibrio della struttura sulla deformata, non mi chiedo quale è l’equilibrio della struttura nella indeformata; mi accorgo che la soluzione è più complessa di quella lineare elastica. Esiste un valore di carico critico Pcrit = formula. Se P<Pcrit si ha soluzione di pura compressibilità. Nel caso di P=Pcrit ho spostamenti laterali di tipo sinusoidale di tipo formula si ha deformazione per instabilità. Questa soluzione di ampiezza arbitraria ‘’a’’ può essere sovrapposta a quella di pura compressione.

Se la trave è tozza cede per snervamento a compressione, se snella insorgono prima del cedimento fenomeni di instabilità elastica.

Finchè il carico è minore del P critico non ho deformazioni laterali (a=0) e la trave è in equilibrio stabile; per P pari a P critico ci sono infiniti valori di ‘’a’’ che rappresentano condizioni di equilibrio indifferente, infine per P>P crit l’unica soluzione esistente è quella compressiva ma in condizione di equilibrio instabile corrispondente ad un massimo di energia potenziale.

E’ importante prevedere quando intervengono questo tipo di sollecitazioni secondarie che nell’intorno della condizione scarica non ho, perché da quel punto in poi il modello lineare non è più valido e si andrà ad utilizzare un apposito modello che verrà esposto in seguito.

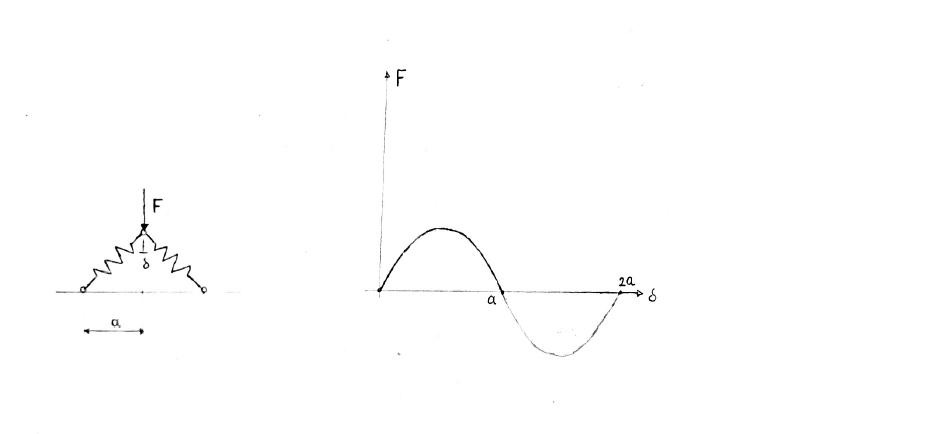
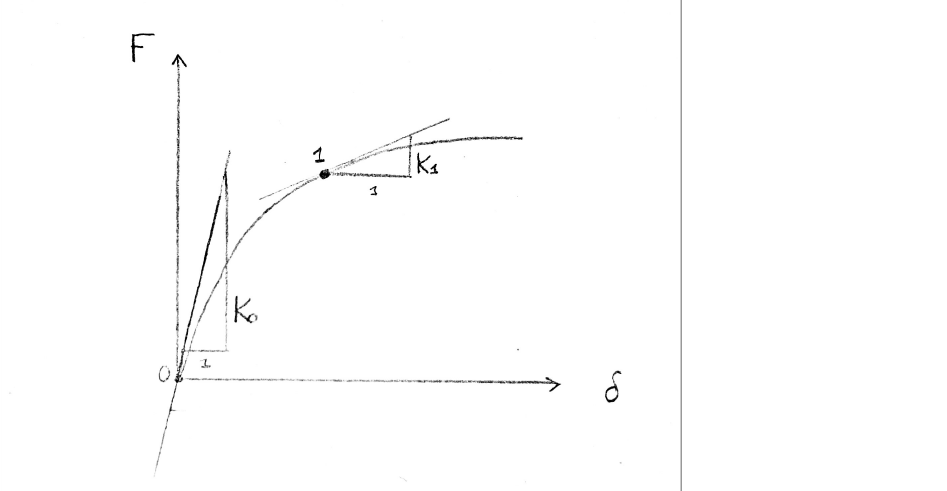
Supponiamo di avere il sistema come in figura, composto da due molle collegate tra loro, soggette alla forza verticale F; di cui si vuole conoscere lo spostamento in funzione del carico; il calcolo di instabilità deve essere fatto attivando la non linearità geometrica, ossia non si possono approssimare le funzioni trigonometriche troncando il loro sviluppo in serie di Taylor al primo ordine, ciò equivale a dire che il sistema farà grandi rotazioni.

Consideriamo dapprima la configurazione indeformata, in cui a carico nullo corrisponde spostamento nullo e individuo un punto del diagramma forza-delta; poi quando le molle sono allineate, il sistema non è in grado di reggere carichi diversi da zero, perché le molle non danno ritorno elastico: quando delta = a, la forza deve essere nulla.

Avendo trovato questi due punti (configurazioni di equilibrio), la forza, nell’intervallo tra essi compresi ha l’andamento come in figura; per delta > a, occorre cambiare segno alla forza, da qui la semionda negativa.

La tangente alla curva in ogni punto è la rigidezza tangente Kt:

Nel punto di massimo Kt=0, mentre nel punto iniziale è quella elastica Kel, condizione in cui le rotazioni possono essere ancora considerate piccole e linearizzabili inoltre se il sistema ha più gradi di libertà Kt non è più uno scalare ma una matrice, e delta e F sono vettori. Posso ricavare la condizione di massimo studiando il comportamento nell’intorno della condizione scarica? La curva si può ricavare anche dal FEM utilizzando un modello non lineare imponendo lo spostamento da 0 a 2a, ma il calcolo è alquanto oneroso.

Analizzo la condizione statica (0): i vettori delta e F sono entrambi nulli, e calcolo la matrice rigidezza della struttura, equivalente alla tangente nel monodimensionale, K0.

Considero una seconda condizione successiva (1), in cui i vettori delta1 e F1 sono diversi da zero( in equilibrio in grandi rotazioni) e individuo la matrice K1; se K1 =K0 posso dire che un sistema è lineare, nel nostro caso, scegliendo una seconda configurazione sufficientemente lontana dalla prima, ho non linearità (K1 diverso da K0). Ora, supponiamo un terzo stato di carico, Fλ, ottenuto per estrapolazione dei due precedenti carichi, (formula), mediante la modulazione del fattore λ e per questo carico ho un’opportuna matrice rigidezza sempre combinazione delle due, supponendo che vari linearmente.

Di questa matrice vogliamo trovare gli autovalori e autovettori (λ, v), per cui si pone il determinante della matrice ottenuta pari a zero, in questo modo oltre alla soluzione lineare, posso ottenere infinte alla 1 altre soluzioni arbitrarie, configurazioni che il sistema raggiunge in uno dei suoi modi propri. Quindi, invece che eseguire un’analisi non lineare, si possono calcolare i valori di λi , con un’analisi modale che è meno onerosa computazionalmente; determinati gli autovalori, possiamo scrivere:

[formule]

Fi rappresenta il carico critico relativo all’autovalore λi.

Nella seconda relazione lo zero rappresenta la variazione del carico e l’autovettore vi la variazione degli spostamenti. Per carico minore di Pcritico il sistema è in equilibrio nella sua configurazione deformata, una volta raggiunto il carico limite, l’evoluzione del sistema è data aggiungendo spostamenti arbitrari senza che il carico vari come posso fare per i moti di corpo rigido cioè posso avere diverse configurazioni di corpo rigido senza modificare i carichi infatti ho condizione di equilibrio più un arbitrario spostamento rigido (vi).

Cliccando Update si aggiorna l’avanzamento del calcolo.

*Open post-file result → deformed shape settings → manual: 10000

*Deformed & original

Col comando *→next si osserva l’evoluzione della deformata al variare della frequenza e avvicinandomi alla risonanza, l’ampiezza delle deformazioni cresce.

Poi a frequenza superiore a quella critica ho cambio di segno degli spostamenti, che in seguito tendono a ridursi. Tutti gli spostamenti sono finiti, anche in prossimità della risonanza.

Ora si vuole monitorare lo spostamento in y del nodo caricato (centro impronta a terra), al fine di calcolare le accelerazioni e le inertanze, pertanto:

*history plot → set location → seleziono il nodo da controllare e do il fine lista

*inc range (campionamento)→ nel terminal scrivo ‘ 0:1 [spazio][spazio] 0: 100000 [invio] 0:1 (passo del campionamento)

*add curves → all locations → frequency, displacement y

*fit

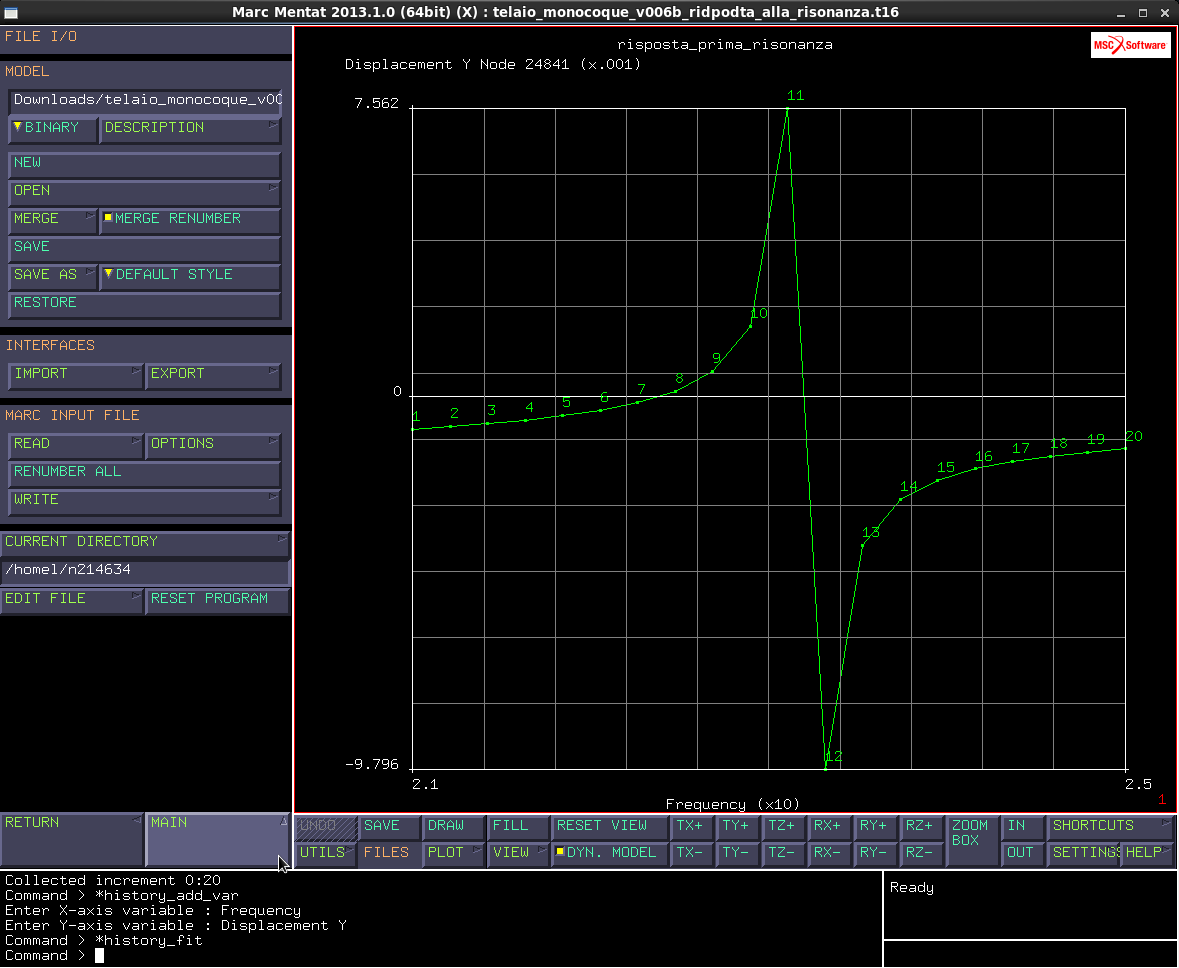
Ottenendo così il grafico.

Dove vedo valori finiti dello spostamento, perché campionando è assai improbabile prendere l’esatta frequenza di risonanza, il programma ci va solamente molto vicino, i valori massimi pertanto, non sono da prendersi come riferimento.

La risposta va bene per campionare i punti tranne quelli di risonanza. I valori massimi individuati non hanno significato fisico, la risposta massima di un sistema non smorzato eccitato è più infinito. Eventualmente inserendo un piccolo smorzamento anche campionando sulla risonanza non ho risposta più infinito con asintoto ma inserisco un taglio la cui quota è inversamente proporzionale allo smorzamento.

Dal wiki apro il file piramide_buckling_base_v000.mfd, di una struttura piramidale dove fare l’analisi di buckling, essa è soggetta a un carico verticale di 1000 N verso il basso applicato al vertice compressivo, mentre la base è vincolata in modo da risultare incastrata al piano; tale struttura è troppo complessa per poter essere studiata con formule analitiche, perché ho equazioni differenziali di secondo grado per ognuna delle 8 travi soggette al carico, che poi sono connesse tra di loro con condizioni al contorno (rotazione e spostamento comune).

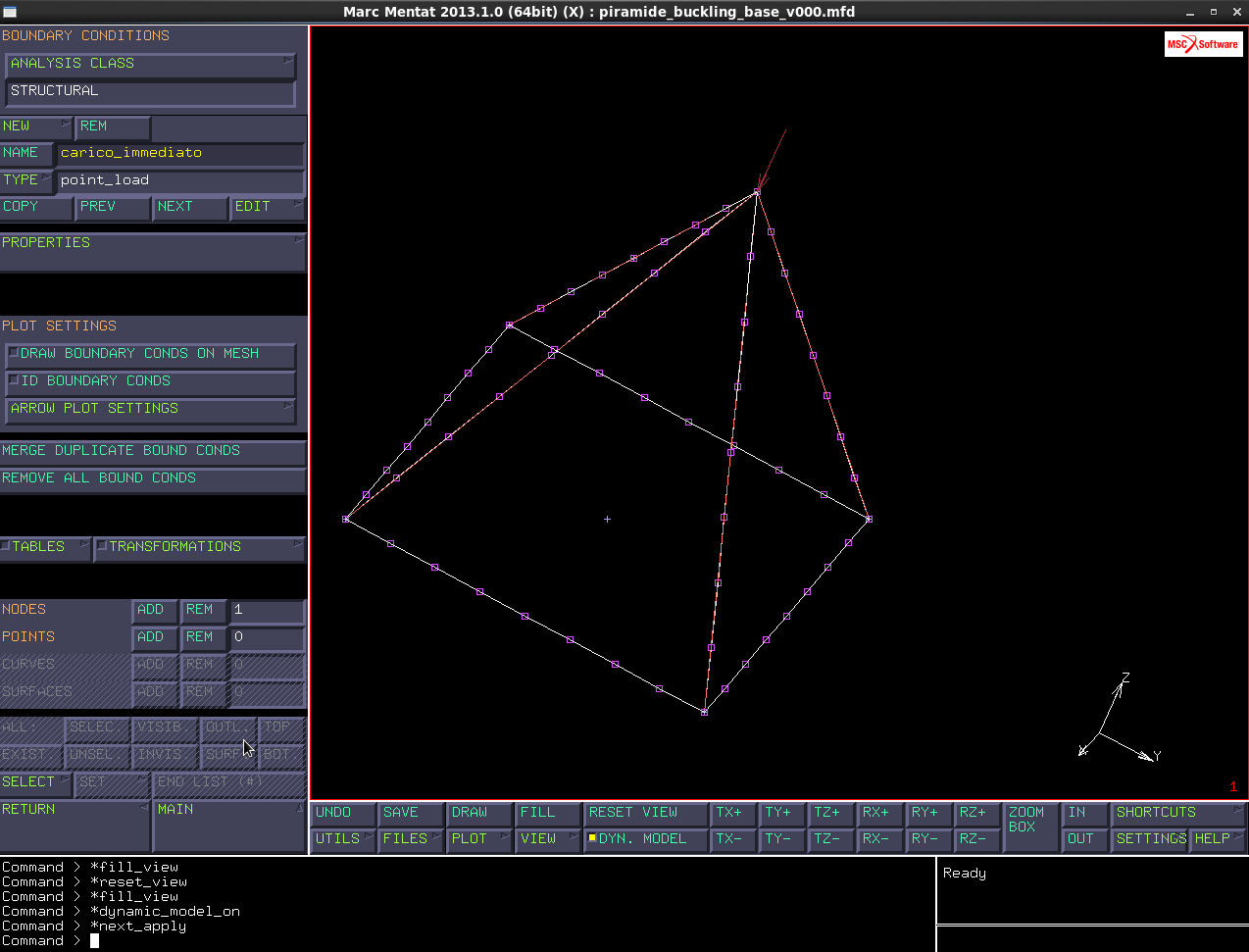
Per cui va fatta un’analisi come descritto in precedenza, per trovare autovalori e autovettori.

Considero due stati di carico: a 0 la struttura è scarica, in 1 ho un carico a piacere che può essere anche il peso proprio della piramide, oppure i 1000 N considerati.

*Loadcase → new → buckle→ name: “ estrazioni fattori modi critici ”

Per ottenere i λ critici, e non metto nessuna proprietà, solo quelle numeriche (defualt).

*Job → new → structural → name : “buckling”

• Properties → initial loads → tutto selezionato, vincoli e sistema di carico stato 1

*→ seleziono il loadcase creato

*Run → submit → open post file

*Open post-file result → deformed shape settings → automatic

Per far vedere il caricamento non lineare, si introduce una piccola perturbazione; un nodo di un lato della piramide non è allineato agli altri, ma lo scostamento è minimo (su 600mm è pari a 1), perciò non è grave.

Se il sistema si comportasse linearmente a 10000 N la deformata sarebbe compressiva.

*→Next e si vede che il primo modo proprio si ha per λ= 8.461, quindi, essendo F0=0 e F1=1000 N, il carico critico è a 8461 N, e la deformata coinvolge tutta la struttura. Oltre tale carico la soluzione ottenuta col modello lineare perde validità, ma non è detto che ci sia il collasso della struttura.

*→Next al secondo modo proprio, per λ= 8.871 ho cedimento su entrambi i lati, poi ho anche modi propri con cedimenti torsionali.

Si aggiunge tale modo proprio:

*job → parameters → buckle nodes = 20

• → Positive bakle nodes = 20

Così facendo si vedono i primi 20 modi di instabilità. Ma è di interesse solo il primo carico critico, che è il carico minimo oltre il quale poi si perde linearità.

*Run → submit.

Cosi facendo, si estraggono i modi e si nota che il terzo è torsionale, per λ=10.1; poi seguono altri modi propri.