Indice
Lezione Progetto del Telaio del 9 maggio 2016 Ing Daniele Spinello - Ferrari GES
Ottimizzazione Strutturale BOZZA
Cos'è l'ottimizzazione?
L'ottimizzazione è quella disciplina che si occupa di cercare di dare ad ogni problema la risposta migliore possibile, ossia la soluzione migliore compatibilmente con i vincoli che ci vengono imposti. I campi di applicazione dell’ottimizzazione strutturale sono molteplici:
- aerospace, in cui è importante il contenimento del peso strutturale per aumentare il possibile carico pagante;
- motorsport, in cui è importante ottenere il minimo peso della struttura mantenendo i requisiti di robustezza e rigidezza;
- automotive, in cui si è avuto, negli ultimi anni, un significativo impulso alla riduzione del peso per migliorare perfomance e consumi e contemporaneamente un aumento dei requisiti di sicurezza imposti, oltre alla necessità di contenere i costi (economie di scala)
Analizzando il flusso tipico di progettazione di un prodotto abbiamo:
- definizione delle specifiche, ovvero la fase zero dello sviluppo, in cui vengono definiti gli obiettivi principali
- da queste specifiche un gruppo di specialisti produrrà un progetto iniziale, abbastanza sommario e rappresentativo, e sicuramente non rispondente ai requisiti (o non in modo ideale) [A]
- a questo punto si passa alla fase di analisi iniziale, che ci consente di estrarre dal progetto iniziale il livello di performance in base ai parametri che vengono stabiliti nella fase di definizione [B]
 Da questo primo loop, con ogni probabilità, uscirà un prodotto con performance inaccettabile, per cui sarà necessaria una serie di revisioni. L’ottimizzazione si va a porre esattamente in questa fase di revisione del progetto, per renderlo più rispondente agli obiettivi, e si va ad integrare con il contributo umano, introducendo quelle caratteristiche di ripetibilità e sostanzialità che prescindono dall’esperienza e della capacità individuale del progettista.
Integrando nello sviluppo del prodotto un’ottimizzazione di tipo formale il processo guadagna molto in robustezza e anche in velocità: basti infatti pensare che questo loop può essere automatizzato, quindi anche prescindendo dalla qualità delle innovazioni introdotte dal progettista, il processo automatico porta sicuramente un guadagno almeno sul fattore tempo.
L'attività di analisi è una parte integrante di tutto il processo di sviluppo prodotto, poiché consente di verificare immediatamente se il progetto modificato sia effettivamente più rispondente agli obiettivi di quanto fosse al loop precedente. Le fasi di analisi e di ottimizzazione sono state sviluppate, a livello applicativo, come due cose distinte; oggi però, tutti i sistemi di ottimizzazione più avanzati presentano queste due fasi del processo integrate, eliminando la perdita di informazioni nel passaggio di dati. L’ottimizzatore dispone direttamente di tutte le variabili/grandezze prodotte dall’analisi, senza bisogno di traduzione delle informazioni da un ambiente all’altro, massimizzando così l’efficienza del loop.
Da questo primo loop, con ogni probabilità, uscirà un prodotto con performance inaccettabile, per cui sarà necessaria una serie di revisioni. L’ottimizzazione si va a porre esattamente in questa fase di revisione del progetto, per renderlo più rispondente agli obiettivi, e si va ad integrare con il contributo umano, introducendo quelle caratteristiche di ripetibilità e sostanzialità che prescindono dall’esperienza e della capacità individuale del progettista.
Integrando nello sviluppo del prodotto un’ottimizzazione di tipo formale il processo guadagna molto in robustezza e anche in velocità: basti infatti pensare che questo loop può essere automatizzato, quindi anche prescindendo dalla qualità delle innovazioni introdotte dal progettista, il processo automatico porta sicuramente un guadagno almeno sul fattore tempo.
L'attività di analisi è una parte integrante di tutto il processo di sviluppo prodotto, poiché consente di verificare immediatamente se il progetto modificato sia effettivamente più rispondente agli obiettivi di quanto fosse al loop precedente. Le fasi di analisi e di ottimizzazione sono state sviluppate, a livello applicativo, come due cose distinte; oggi però, tutti i sistemi di ottimizzazione più avanzati presentano queste due fasi del processo integrate, eliminando la perdita di informazioni nel passaggio di dati. L’ottimizzatore dispone direttamente di tutte le variabili/grandezze prodotte dall’analisi, senza bisogno di traduzione delle informazioni da un ambiente all’altro, massimizzando così l’efficienza del loop.

Coi tempi della F1 tutto ciò assume la massima importanza, perché l'esecuzione di un maggior numero di calcoli consente di avvicinarsi maggiormente all’ottimo, e perciò farli velocemente fa la differenza. Per questo in F1 si spinge tantissimo sull’ottimizzazione, tanto che forse, per intensità di investimenti, sono i maggiori utilizzatori, anche perché va fatto tutto al primo tentativo altrimenti si sforano i tempi (il telaio viene congelato a settembre e le revisioni di progetto da un anno all’altro sono abbastanza sostanziali - spesso il telaio è all’80% nuovo - e il tutto deve essere completato nel giro di 6-7 mesi, mentre un telaio automotive stradale ha una genesi di 1,5/2 anni).
Aspetti formali di definizione del problema
 Il problema generale di ottimizzazione si formula in questi termini: l’obiettivo è trovare il minimo di una F(x) sul dominio x. Dicendo minimo si coprono tutte le possibili casistiche, perché nel caso dovessimo trovare un massimo basta cambiare di segno la funzione.
La F(x) è soggetta a due tipi di vincoli:
Il problema generale di ottimizzazione si formula in questi termini: l’obiettivo è trovare il minimo di una F(x) sul dominio x. Dicendo minimo si coprono tutte le possibili casistiche, perché nel caso dovessimo trovare un massimo basta cambiare di segno la funzione.
La F(x) è soggetta a due tipi di vincoli:
- behavioural constraints, ovvero le funzioni che dal punto di vista pratico impongono dei vincoli per rendere fisico il processo di ottimizzazione (es. massa > 0, tensione massima nella struttura < della massima ammissibile dal materiale, ecc..)
- side constraints, cioè i vincoli che danno una prescrizione sul margine di variabilità della variabile x, definendo quindi il margine di manovra sulle grandezze in input.
Questa è la formulazione più generale possibile, ma partire da questa si possono fare vari distinguo, in base alla natura delle funzioni e delle variabili:
- le funzioni possono essere lineari o non lineari
- i vincoli possono essere presenti o meno,
- l’ottimizzazione può essere continua, se le variabili possono assumere tutti i valori reali, o discreta, se le variabili possono assumere solo alcuni valori
- si può avere un solo obiettivo oppure più di uno
- si può avere un solo punto di minimo oppure più di uno
- l’ottimizzazione può essere deterministica o non deterministica, nel caso in cui non conosciamo con esattezza il valore di una variabile (es. spessore di un lamierato: ha un valore nominale ma c’è una tolleranza, quindi è descritto solo in termini statistici; è stata sviluppata una base teorica che tratta l’ottimizzazione di grandezze definite in termini statistici, estraendo le caratteristiche statistiche dell’obiettivo e del minimo a partire dalla distribuzione delle grandezze di input).
Applicazione pratica
Esempio
Poniamo di essere in montagna e di trovarci in un punto (stella nell'immagine). L’obiettivo è arrivare al punto più basso (minimo) della valle, nel modo più rapido possibile. Come procediamo? Ci guardiamo intorno, cerchiamo di capire qual è la direzione che ci consente di scendere più rapidamente, e la imbocchiamo; quando siamo a metà strada verifichiamo nuovamente se è la direzione migliore in base al nuovo panorama che vediamo, e così via: per step iterativi, andremo a raggiungere una posizione per cui muovendoci in qualunque direzione non scendiamo più, e quindi siamo arrivati al punto di minimo.
Applichiamo ora il metodo contenuto nell'esempio in ambito astratto, quindi ad una funzione di cui non si conosce l'andamento. Siamo quindi nella stessa condizione ma non abbiamo punti di riferimento. La soluzione più ovvia è quella di calcolare tutti i punti della funzione, analizzare l’andamento della superficie e, in base a ciò, decidere in che direzione compiere il primo passo. Nella pratica questo tipo di approccio non è facilmente applicabile, poiché riuscire ad individuare ogni singolo punto della superificie è un processo abbastanza dispendioso, in termini di tempo e capacità di calcolo: serve un metodo più efficiente. Si può però restringere il campo di calcolo della funzione ad un intorno del punto di partenza di ogni iterazione, in modo da “tastare” localmente l'andamento, e prendere quindi la direzione più conveniente.
Dal punto di vista analitico, trovare la pendenza di una superificie in un suo punto, nota la funzione F, equivale a trovarne il gradiente, cioè il vettore che ha come componenti le derivate parziali della funzione in tutte le singole variabili. Il gradiente di fatto individua, di una superficie, la direzione di maggiore ripidità. Perciò, per trovare il punto di minimo, si prende il negativo del gradiente. Questo viene chiamato S, e il metodo che fa uso di questo gradiente negativo è detto metodo steep descent.
 Se partiamo da un punto X0, valutiamo S, che ci darà la direzione in cui muoverci, e ci muoviamo nel punto X1, che sarà individuato dalla formula X1 = X0 + alpha*S, dove alpha è uno scalare. Iterativamente, spostandoci di una quantità che dipende da quanto varia la funzione, andiamo a convergere fino a un punto in cui la funzione ha gradiente nullo, cioè non cresce più in nessuna direzione. Questo è il nostro punto di minimo.
Se abbiamo un vincolo sulle variabili utilizziamo la stessa logica, ma, quando tocchiamo la frontiera del campo di libertà della variabile, ci muoviamo lungo di essa fino a trovare il punto di minimo compatibile col vincolo.
Se partiamo da un punto X0, valutiamo S, che ci darà la direzione in cui muoverci, e ci muoviamo nel punto X1, che sarà individuato dalla formula X1 = X0 + alpha*S, dove alpha è uno scalare. Iterativamente, spostandoci di una quantità che dipende da quanto varia la funzione, andiamo a convergere fino a un punto in cui la funzione ha gradiente nullo, cioè non cresce più in nessuna direzione. Questo è il nostro punto di minimo.
Se abbiamo un vincolo sulle variabili utilizziamo la stessa logica, ma, quando tocchiamo la frontiera del campo di libertà della variabile, ci muoviamo lungo di essa fino a trovare il punto di minimo compatibile col vincolo.

Ottimizzazione discreta
Normalmente, gli elementi strutturali con cui si ha a che fare sono disponibili solo con dimensioni discrete (es. viteria, spessori lamine/pelli, ecc…). É necessario, perciò, utilizzare una variabile che possa assumere solo valori discreti (o discontinui), e per ottenere questo ci sono varie strategie possibili. La strategia più semplice consiste nel trovare il minimo con valori continui, e poi arrotondare al valore immediatamente superiore o inferiore. Una logica più raffinata è il conservative discrete design, che consiste nello scegliere, per ogni variabile che possa assumere solo valori discreti, il valore immediatamente precedente o successivo a quello ottimale, optando per quello che viola meno i vincoli. Questo richiede, in fase di analisi, definito n il numero di variabili di progetto, un numero pari 2*n simulazioni. Una logica ancor più sofisticata è il design of experiments, dove per ogni variabile per la quale abbiamo un valore finale dell’ottimizzazione che cade tra 2 valori discreti candidati, si fa una verifica di quello che succede facendo assumere alla variabile il valore immediatamente precedente o successivo, coprendo però tutte le combinazioni possibili. In questo caso il numero di simulazioni diventa molto più elevato, pari a 2^n simulazioni, il che porta a tempi di elaborazione inaccettabili per ogni iterazione. Fortunatamente ci sono algoritmi che consentono di estrarre, da una popolazione di variabili di partenza, dei campioni statisticamente rappresentativi, permettendo di limitiare il numero di verifiche a 2^16, limite ritenuto accettabile.
Ottimizzazione multi-obiettivo
 Spesso capita di avere più obiettivi in fase di progetto, spesso in antitesi l’uno rispetto all’altro (es. massimizzare le prestazioni minimizzando i consumi, massimizzare la sicurezza passiva minimizzando il peso, ecc..). É pertanto necessario fare qualche considerazione accessoria. Vediamo due funzioni i cui punti di minimo sono individuati separatamente (figura). Se ci poniamo sul punto M1 (minimo della funzione 1) vediamo che la funzione 1 è al suo minimo, ma la funzione 2 è ben distante dal minimo. Le stesse considerazioni si applicano al punto M2. Supponiamo ora di voler cercare, a partire da M1, dei valori che rendono la funzione 2 più vicina al valore minimo: notiamo che, se ci muoviamo nella direzione in cui la funzione 2 decresce, questo va a scapito del minimo della funzione 1, e viceversa partendo da M2. I punti compresi tra M1 ed M2 sono detti punti ottimali secondo Pareto, ed individuano le funzioni non di ottimo, ma di miglior compromesso tra due funzioni obiettivo che hanno minimi di funzione diversi.
Se trasferiamo queste due funzioni in uno spazio detto spazio delle funzioni obiettivo, in cui mettiamo sulle ascisse i valori della funzione 1, e sulle ordinate i valori della funzione 2, otteniamo è la frontiera di Pareto, che individua l’insieme delle configurazioni che danno il risultato di miglior compromesso tra due obiettivi in conflitto. Questa curva è molto utilizzata nella pratica ingegneristica, e aiuta nello stabilire come muoversi per ottenere il compromesso desiderato. Ad esempio, se vogliamo dare priorità alla riduzione della funzione 2, potremo andare a scegliere una soluzione nell’intorno del punto B e vediamo che nell’intorno del punto B, dove la funzione 2 ha un margine di variabilità abbastanza alto senza che questo risulti in una variazione elevata per la funzione 1. Viceversa, se vogliamo dare priorità alla riduzione della funzione 1, potremo andare a scegliere una soluzione nell’intorno del punto C, dove abbiamo un margine di variabilità abbastanza ampio per la funzione 1 senza che questo risulti in una perdita eccessiva per la funzione 2.
Nei casi più complicati, in cui non è possibile una rappresentazione grafica su due assi, si richiedono metodi più complessi, che possono, per esempio, ridurre una ottimizzazione multi-obiettivo ad una ottimizzazione mono-obiettivo utilizzando come funzione macro-obiettivo una funzione F che sia la combinazione delle funzioni obiettivo individuali. La funzione F può essere costruita con vari metodi, quali, per esempio, una somma pesata dei vari termini delle funzioni obiettivo individuali, lavorando anche sui coefficienti per assegnare una priorità (un coefficiente maggiore darà maggior peso alla funzione).
Spesso capita di avere più obiettivi in fase di progetto, spesso in antitesi l’uno rispetto all’altro (es. massimizzare le prestazioni minimizzando i consumi, massimizzare la sicurezza passiva minimizzando il peso, ecc..). É pertanto necessario fare qualche considerazione accessoria. Vediamo due funzioni i cui punti di minimo sono individuati separatamente (figura). Se ci poniamo sul punto M1 (minimo della funzione 1) vediamo che la funzione 1 è al suo minimo, ma la funzione 2 è ben distante dal minimo. Le stesse considerazioni si applicano al punto M2. Supponiamo ora di voler cercare, a partire da M1, dei valori che rendono la funzione 2 più vicina al valore minimo: notiamo che, se ci muoviamo nella direzione in cui la funzione 2 decresce, questo va a scapito del minimo della funzione 1, e viceversa partendo da M2. I punti compresi tra M1 ed M2 sono detti punti ottimali secondo Pareto, ed individuano le funzioni non di ottimo, ma di miglior compromesso tra due funzioni obiettivo che hanno minimi di funzione diversi.
Se trasferiamo queste due funzioni in uno spazio detto spazio delle funzioni obiettivo, in cui mettiamo sulle ascisse i valori della funzione 1, e sulle ordinate i valori della funzione 2, otteniamo è la frontiera di Pareto, che individua l’insieme delle configurazioni che danno il risultato di miglior compromesso tra due obiettivi in conflitto. Questa curva è molto utilizzata nella pratica ingegneristica, e aiuta nello stabilire come muoversi per ottenere il compromesso desiderato. Ad esempio, se vogliamo dare priorità alla riduzione della funzione 2, potremo andare a scegliere una soluzione nell’intorno del punto B e vediamo che nell’intorno del punto B, dove la funzione 2 ha un margine di variabilità abbastanza alto senza che questo risulti in una variazione elevata per la funzione 1. Viceversa, se vogliamo dare priorità alla riduzione della funzione 1, potremo andare a scegliere una soluzione nell’intorno del punto C, dove abbiamo un margine di variabilità abbastanza ampio per la funzione 1 senza che questo risulti in una perdita eccessiva per la funzione 2.
Nei casi più complicati, in cui non è possibile una rappresentazione grafica su due assi, si richiedono metodi più complessi, che possono, per esempio, ridurre una ottimizzazione multi-obiettivo ad una ottimizzazione mono-obiettivo utilizzando come funzione macro-obiettivo una funzione F che sia la combinazione delle funzioni obiettivo individuali. La funzione F può essere costruita con vari metodi, quali, per esempio, una somma pesata dei vari termini delle funzioni obiettivo individuali, lavorando anche sui coefficienti per assegnare una priorità (un coefficiente maggiore darà maggior peso alla funzione).
Punti di minimo plurimi
 Esistono casi in cui il punto di minimo non è unico, ma ne esiste più di uno. Da un punto di vista grafico la soluzione è ovvia, ma diventa più complicata nel caso in cui non si conosca l’andamento delle funzioni. Con riferimento alla figura, se abbiamo una funzione come quella nel grafico a sinistra, da qualsiasi punto di partenza si convergerà nel punto di minimo A. Se invece abbiamo una funzione come quella nel grafico a destra, a seconda del punto di partenza si convergerà sul punto P o sul punto Q. Nessuno dei 2 è errato, ma Q è una soluzione migliore rispetto a P. La logica utilizzata dagli ottimizzatori è quella di utilizzare un numero elevato di punti di partenza, ben sparpagliati, in modo tale da riuscire a coprire il più possibile lo spazio delle variabili, ed individuare così la miglior soluzione.
Esistono casi in cui il punto di minimo non è unico, ma ne esiste più di uno. Da un punto di vista grafico la soluzione è ovvia, ma diventa più complicata nel caso in cui non si conosca l’andamento delle funzioni. Con riferimento alla figura, se abbiamo una funzione come quella nel grafico a sinistra, da qualsiasi punto di partenza si convergerà nel punto di minimo A. Se invece abbiamo una funzione come quella nel grafico a destra, a seconda del punto di partenza si convergerà sul punto P o sul punto Q. Nessuno dei 2 è errato, ma Q è una soluzione migliore rispetto a P. La logica utilizzata dagli ottimizzatori è quella di utilizzare un numero elevato di punti di partenza, ben sparpagliati, in modo tale da riuscire a coprire il più possibile lo spazio delle variabili, ed individuare così la miglior soluzione.
Esempio
Prendiamo una struttura semplice, con dei requisiti di prodotto, di cui minimizzare una funzione di costo. É un problema semplice ma richiede un approccio articolato.
 La struttura è una colonna, vincolata con 2 cerniere alla base e al punto più alto, su cui abbiamo un carico P. Vogliamo definire le caratteristiche in termini di diametro medio e di spessore in modo da minimizzare il costo, che è definito dalla funzione C. Abbiamo due behavioural constraints, il primo dei quali stabilisce che la tensione media sulla sezione debba essere inferiore alla tensione ammissibile (del materiale), mentre il secondo impone che la tensione sia sempre inferiore al carico di buckling; inoltre abbiamo due side constraints, che definiscono lo spazio di variabilità sia del diametro medio che dello spessore.
Il primo passo consiste nel formulare il problema secondo il formalismo utilizzato per la definizione generale di ottimizzazione: prendiamo una variabile X, data da un vettore con componenti x1 e x2, a cui noi assegnamo diametro medio d e spessore t. In questi termini ridefiniamo la funzione costo C in funzione di X, così come i vincoli.
Ora possiamo creare un grafico, in cui avremo sulle ascisse il diametro medio e sulle ordinate lo spessore. Disegniamo i side constraints, che assumeranno la forma di un rettangolo entro il quale dobbiamo muoverci. Disegniamo poi l’andamento della tensione statica, in funzione di d e t, esplicitato in t: otteniamo una iperbole, ed essendo una disuguaglianza questa restringerà il nostro spazio alla zona situata a destra della curva. Disegniamo infine il vincolo sulla tensione di buckling, in funzione di d e t, esplicitato in t: ne risulta un’altra iperbole, che limita ulteriormente il nostro spazio alla zona situata alla sua destra.
La struttura è una colonna, vincolata con 2 cerniere alla base e al punto più alto, su cui abbiamo un carico P. Vogliamo definire le caratteristiche in termini di diametro medio e di spessore in modo da minimizzare il costo, che è definito dalla funzione C. Abbiamo due behavioural constraints, il primo dei quali stabilisce che la tensione media sulla sezione debba essere inferiore alla tensione ammissibile (del materiale), mentre il secondo impone che la tensione sia sempre inferiore al carico di buckling; inoltre abbiamo due side constraints, che definiscono lo spazio di variabilità sia del diametro medio che dello spessore.
Il primo passo consiste nel formulare il problema secondo il formalismo utilizzato per la definizione generale di ottimizzazione: prendiamo una variabile X, data da un vettore con componenti x1 e x2, a cui noi assegnamo diametro medio d e spessore t. In questi termini ridefiniamo la funzione costo C in funzione di X, così come i vincoli.
Ora possiamo creare un grafico, in cui avremo sulle ascisse il diametro medio e sulle ordinate lo spessore. Disegniamo i side constraints, che assumeranno la forma di un rettangolo entro il quale dobbiamo muoverci. Disegniamo poi l’andamento della tensione statica, in funzione di d e t, esplicitato in t: otteniamo una iperbole, ed essendo una disuguaglianza questa restringerà il nostro spazio alla zona situata a destra della curva. Disegniamo infine il vincolo sulla tensione di buckling, in funzione di d e t, esplicitato in t: ne risulta un’altra iperbole, che limita ulteriormente il nostro spazio alla zona situata alla sua destra.
 A questo punto non resta che disegnare la funzione di costo C in funzione di d e t, che si presenta come una serie di iperboli, ad ognuna delle quali corrisponde un valore di C. Avendo limitato lo spazio delle variabili, possiamo escludere tutte le iperboli che non ricadono nello spazio ammissibile, in quanto rappresentano soluzioni del problema che violano i vincoli imposti. Tra tutte le iperboli che intersecano lo spazio ammissibile, e quindi rappresentano soluzioni ammissibili, scegliamo quella corrispondente al minor costo (C = 0,64). Essa tocca lo spazio delle soluzioni ammissibili in un solo punto, al quale corrispondono un valore di diametro medio ed uno di spessore, e che saranno soluzione del problema.
A questo punto non resta che disegnare la funzione di costo C in funzione di d e t, che si presenta come una serie di iperboli, ad ognuna delle quali corrisponde un valore di C. Avendo limitato lo spazio delle variabili, possiamo escludere tutte le iperboli che non ricadono nello spazio ammissibile, in quanto rappresentano soluzioni del problema che violano i vincoli imposti. Tra tutte le iperboli che intersecano lo spazio ammissibile, e quindi rappresentano soluzioni ammissibili, scegliamo quella corrispondente al minor costo (C = 0,64). Essa tocca lo spazio delle soluzioni ammissibili in un solo punto, al quale corrispondono un valore di diametro medio ed uno di spessore, e che saranno soluzione del problema.

Ottimizzazione: metodi pratici
Size optimization
Il primo metodo di ottimizzazione che è stato sviluppato è il metodo di Size Optimization. Secondo questo metodo si parte da una struttura che ha una forma assegnata. Di questa struttura si variano i parametri strutturali che assumono il significato di variabili. I parametri strutturali sono per esempio lo spessore, i diametri, le dimensioni delle sezioni; sono variabili parametrizzate a seconda delle caratteristiche geometriche della struttura.
Partendo da una struttura di questo tipo in cui non si fa particolare attenzione ai vincoli di robustezza, ci si pone il problema di trovare una struttura di peso minimo che ci garantisca una deformata massima sotto un determinato carico.
 L’ottimizzazione di tipo size va ad aumentare le sezioni che lavorano di più e va a ridurre le sezioni che non danno un grosso contributo dal punto di vista del vincolo.
L’ottimizzazione di tipo size va ad aumentare le sezioni che lavorano di più e va a ridurre le sezioni che non danno un grosso contributo dal punto di vista del vincolo.
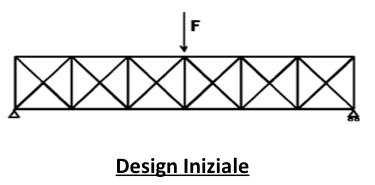 Da notare che nonostante la struttura sia stata ridimensionata la forma è rimasta la stessa, sarà poi compito del progettista valutare se mantenere gli elementi strutturali che sono stati ridotti.
Da notare che nonostante la struttura sia stata ridimensionata la forma è rimasta la stessa, sarà poi compito del progettista valutare se mantenere gli elementi strutturali che sono stati ridotti.
Shape optimization
Un altro tipo di ottimizzazione che si usa in ambito strutturale è l’ottimizzazione di forma. Il grosso della forma della struttura è assegnato, quello che l’ottimizzazione fa variare è la forma delle caratteristiche geometriche della struttura in particolare i raggi di raccordo, forme di alleggerimento, le grandezze che caratterizzano la geometria fine della struttura.
La shape optimization partirà dalla configurazione iniziale e andrà a perturbare la forma delle caratteristiche geometriche secondo quelli che sono dei vettori di perturbazione (pi). I vettori di perturbazione sono definiti dall’utente.
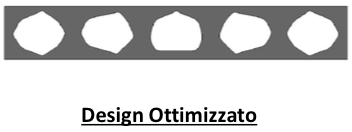 La forma finale sarà una combinazione lineare di questi vettori. L’ottimizzazione ha come scopo quello di trovare la combinazione dei coefficienti di scalatura dei vettori di perturbazione ottimale che ci garantisce il rispetto dei vincoli mantenendo il peso più basso.
La forma finale sarà una combinazione lineare di questi vettori. L’ottimizzazione ha come scopo quello di trovare la combinazione dei coefficienti di scalatura dei vettori di perturbazione ottimale che ci garantisce il rispetto dei vincoli mantenendo il peso più basso.
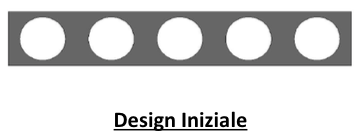 L’entità della deformazione dipende dalla quantità dei vettori di perturbazione che si usano.
L’entità della deformazione dipende dalla quantità dei vettori di perturbazione che si usano.
Topography optimization
Un caso particolare di shape Optimization è la Topography Optimization. In questo tipo di ottimizzazione, le funzioni di deformazione anziché essere definite dall’utente sono già precostituite. Le funzioni che si usano sono già inserite all’interno delle simulazioni e vengono parametrizzate da un numero limitato di parametri.
Vengono tipicamente utilizzate per lamierati o pareti a spessore costante.
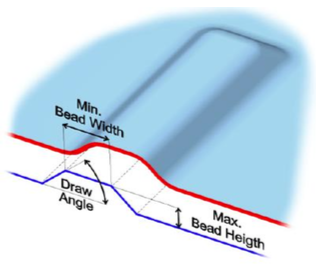
Esempio topography Optimization: L’obbiettivo di questa ottimizzazione è quello di ridurre il più possibile la deformabilità del punto di applicazione del puntone di sospensione. L’ottimizzazione di forma va a costruire dei corrugati attorno al supporto. Questi sono i risultati appena dopo dall’ottimizzazione, il passo successivo è quello di creare un modello più ingegnerizzato.

Topology optimization
Abbiamo visto fino ad ora tipi di ottimizzazione che non ci danno indicazioni su come cambiare la forma della struttura in modo da renderla più efficiente. Per avere un’ottimizzazione che ci dica qual è la distribuzione migliore del materiale che massimizza un certo tipo di performance strutturale è l’ottimizzazione topologica. E’ il tipo di ottimizzazione che da più indicazioni dal punto di vista progettuale. Non c’è bisogno di scegliere una forma della struttura, l’unico vincolo che abbiamo è quello di assegnare la massima libertà possibile all’ottimizzazione. Bisogna far occupare alla struttura di partenza la più grande quantità di volume a disposizione.
L’ottimizzazione si occuperà di scaricare la struttura del materiale inutile, ma in modo tale da mantenere i vincoli assegnati.

Come risultato ci si aspetta una struttura con una buona distinzione tra parti piene e parti vuote, quello che sarebbe interessante vedere è una soluzione di tipo binario cioè vedere se una parte funziona al 100% e una parte invece che non funziona. Non è utile vedere delle zone grigie cioè con delle parti che collaborano un po’ si un po’ no.

L’ottimizzazione topologica può essere vista come un’ottimizzazione di size portata all’estremo in cui la variabile di progetto è la densità di ogni singolo elemento di cui la struttura è costituita. Tipicamente viene fatta su modelli di strutture a elementi finiti in cui le strutture vengono divise in una serie di cellette ognuna delle quali ha un comportamento relativamente semplice da descrivere. Di contro per avere un buon risultato è necessario utilizzare un numero molto grande di queste cellette.
Ogni rigidezza e densità delle cellette diventa variabile di progetto per cui anche su una struttura piuttosto semplice il numero delle variabili diventa difficile da gestire soprattutto per un ottimizzazione di tipo discreto. Si è quindi deciso di trasformare questo tipo di ottimizzazione da discreta a continua facendo variare la densità del materiale tra il valore nominale e il valore 0. Pensiamo di mettere una relazione lineare tra la densità e la sua rigidezza, con questo tipo di relazione il risultato dell’ottimizzazione sarà una struttura povera dal punto di vista costruttivo. Per ovviare a questo problema è stato introdotto un termine di penalizzazione in modo di non avere una legge lineare.
Utilizzando queste curve riusciamo ad avere come risultato dell’ottimizzazione delle strutture che hanno una suddivisione molto più netta tra quelle che sono le zone di materiale che lavora molto e le zone di materiale che lavora poco. La topologica è uno strumento molto utile per le strutture a trave.
Ottimizzazione: esempi pratici
Esempio: pedale freno con carico applicato sulla pedana
 Imponiamo che lo spostamento delta sia inferiore a un certo limite, vogliamo trovare la forma che deve avere per avere il peso più basso.
Il volume della struttura è diviso in due parti: una parte è quella designabile l’altra parte è quella che non può essere modificata.
Ottimizzazione di tipo topologico:
Imponiamo che lo spostamento delta sia inferiore a un certo limite, vogliamo trovare la forma che deve avere per avere il peso più basso.
Il volume della struttura è diviso in due parti: una parte è quella designabile l’altra parte è quella che non può essere modificata.
Ottimizzazione di tipo topologico:
creare un modello a elementi finiti della struttura: la struttura è stata sostituita a una mesh piuttosto fine e sono stati assegnati a questi elementi delle proprietà di un materiale che può essere simile all’alluminio.

Si applica il metodo dell’ottimizzazione topologica secondo il modello di materiale isotropo con il penalty factor di 4. Quello che risulta è una distribuzione del materiale secondo le densità. dalla mappa risultante delle densità si possono notare 2 cose: il materiale non designabile è rimasto al suo valore di densità nominale
il materiale designabile della struttura invece è variato; una porzione della struttura è a densità molto basse, la parte restante è a densità 1.
Si nota che la transizione tra materiale a bassa densità e il materiale a alta densità è compressa, il che è un risultato positivo, c’è una separazione piuttosto netta tra la parte di materiale che collabora e la parte di materiale che è superflua.
Non sappiamo molto però dal punto di vista delle indicazioni costruttive. Per avere delle indicazioni più ingegneristiche si possono tagliare le porzioni di materiale che hanno densità sotto un certo limite
 Si può notare che le parti rosse della mappa di densità sono sopravvissute.
Molta parte della struttura iniziale è stata eliminata perché evidentemente ai fini dell’ottimizzazione non dava alcun contributo.
Si può notare che le parti rosse della mappa di densità sono sopravvissute.
Molta parte della struttura iniziale è stata eliminata perché evidentemente ai fini dell’ottimizzazione non dava alcun contributo.
Questo tipo di forma è sicuramente la più efficiente, ma purtroppo non è realizzabile.
Per rendere la strutture realizzabili sono inseriti all’interno delle simulazioni dei codici di vincolo che vanno a interagire con il processo di ottimizzazione in modo tale da indirizzarlo a produrre delle strutture che siano compatibili con dei metodi di produzione standard.
 Per esempio si può imporre che la geometria finale possa essere realizzata per fusione o estrusione. Si possono anche inserire dei vincoli più complessi tale per cui la struttura finale presenti una simmetria. Il risultato finale è molto simile a quella che sarà la realizzazione
Per esempio si può imporre che la geometria finale possa essere realizzata per fusione o estrusione. Si possono anche inserire dei vincoli più complessi tale per cui la struttura finale presenti una simmetria. Il risultato finale è molto simile a quella che sarà la realizzazione
Esempio: ottimizzazione compositi laminati
Le strutture in carbonio vengono costruite mettendo su degli stampi una sequenza di pelli, dando orientazione e spessore in base al tipo di carichi ed al comportamento che si vuole fare assumere alla struttura. In questo caso le variabili di costruzione della nostra struttura non sono solo i volumi di partenza ma possiamo variare:
- Il numero di pelli, cioè quanto spessore diamo ad ogni singola porzione della struttura;
- La forma delle pelli: tutte le pelli ricoprono la struttura oppure possiamo tagliarle e metterne di più nelle zone più caricate;
- Orientazione delle pelli: i compositi, in particolare gli unidirezionali, hanno delle caratteristiche diverse di rigidezza a seconda che vengano sollecitati nella direzione longitudinale o trasversale. La direzione longitudinale, inoltre può essere orientata secondo un sistema di assi sulla struttura, a seconda del risultato che si vuole raggiungere in termini di deformata e di carichi della struttura stessa;
- Materiale delle pelli;
- Sequenza di laminazione: a parità del numero di pelli si possono ottenere dei comportamenti diversi a seconda di come vengono messe le pelli l’una su l’altra. Un problema di questo tipo è quello tipico per cui si devono affrontare le tematiche per ottimizzazione di valori discreti, in quanto le pelli sono disponibili in una varietà limitata di spessori che tipicamente vanno da 2*10^(-4) a 4*10^(-4) mm.
Si divide anche qui la struttura in No Design Volume ed Design Volume e come nel caso dell’ottimizzazione topologica dovremmo partire da una struttura che è sovrabbondante, in senso di materiale composito, cioè in termini di numero, orientamento e spessore delle pelli; in modo tale da dare all’ottimizzatore la possibilità di andare ad eliminare la parte che non serve e tenere solo quella che utile. Questo tipo di algoritmo di ottimizzazione viene denominata ottimizzazione free-size che risulta essere il corrispettivo dell’ottimizzazione topologica applicata ai compositi. Il termine size indica che si va a variare lo spessore delle pelli mentre free perché non si lavora sulle macro aree della struttura, ma ogni singolo elemento ha una variabile che può variare indipendentemente dalle altre e quindi diventa ottimizzabile. Nell’esempio in figura sono stati utilizzati 5 spessori dove ogni colore rappresenta un orientamento ed un materiale. Tipicamente nelle strutture complesse non si conoscono a priori le zone più sollecitate e quindi si cerca di mettere un numero di pelli sovrabbondanti con materiale, spessore ed orientazione variabili per coprire la struttura a 360°. L’ottimizzazione Free-Size ci darà una distribuzione di spessore anziché una distribuzione di densità.
Come si vede dalla figura sopra, ci sono delle zone che vengono scaricate molto (esempio la parte superiore cerchiata in rosso) e zone invece caricate di più (zone colorate in rosso).
Gli spessori sono ottenuti tramite una sequenza di pelli che vengono ridisegnate e ritarate, con lo spessore a seconda del materiale, dall’ottimizzazione. L’ottimizzatore produce una sequenza di pelli di forma e spessore variabili, che sono il primo risultato del processo di ottimizzazione di questa parte in composito.
Questa fase elimina dalle variabili la forma delle pelli, perché bisogna ottimizzare solo lo spessore. Quindi, non si ha più una Free-Size Optimization perché la forma è stata definita, ma si ha un’ottimizzazione meno complessa che è solo una Size.
Questa sarebbe un’ottimizzazione ottimale ma in realtà bisogna fare alcune considerazioni:
- Se si guardano bene le pelli si notano alcune con spessore molto basso e altre con spessore molto alto, quindi ci sono delle pelli che dal punto di vista del risultato non daranno un grosso contributo mentre altre guideranno il comportamento della struttura.
- Le pelli avranno sicuramente delle forme ottimali dal punto di vista della geometria, ma per quanto riguarda la fase costruttiva, risultano essere scomode per via della forma delle stesse.
In merito a queste considerazioni, bisogna quindi, rendere le forme delle pelli ingegnerizzabili (semplici e fattibili costruttivamente) ed in più eliminare le pelli con spessore troppo piccolo in quanto non daranno un grosso contributo ai fini del risultato. Tuttavia non bisogna stravolgere completamente la forma, in quanto, più ci si sposta dal modello dato come risultato dall’ottimizzatore e più ci si discosta dal punto di ottimo.
In questa sequenza di tre immagini delle fasi dell’ottimizzazione Size, le pelli descritte in precedenza vengono disposte e sequenziate sulla struttura facendo variare lo spessore, finché nel rispetto dei vincoli non si raggiunge il punto di ottimo che corrisponde alla minore massa della struttura. Come risultato finale si avrà un Layout più regolare ed una distribuzione di pelli fisicamente realizzabile, con spessori distribuiti nelle zone della struttura più sollecitate.
Come ben noto, un laminato ha caratteristiche diverse a seconda del fatto che certi tipi di materiale si trovino a metà dello spessore oppure verso l’estremità dello stesso. Inoltre, ci sono delle altre considerazioni di tipo costruttivo, le quali consigliano che la prima pelle in una struttura in laminato non sia unidirezionale ma in tessuto; questo perché la struttura risulta così più robusta e compatta con maggiore facilità di laminazione sulla stessa. In sostanza, con le considerazioni sopra fatte, si potrebbe compiere un ulteriore passo, che consiste nella ricercare dell’orientazione ottimale nella sequenza delle pelli.Passo che comunque non comporta una variazione ulteriore di peso della struttura. E stato descritto un metodo di ottimizzazione topologica con due percorsi alternativi ma potrebbero esistere altre ottimizzazioni con l’integrazione tra i diversi metodi a diversi livelli di avanzamento del progetto.
















Discussione
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
I passaggi e le immagini rispettano le regole di composizione e il testo risulta fruibile.
Il testo proposto è coerente con gli appunti personali del revisore?
La trattazione è completa e coerente con gli appunti.
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
Non credo andrebbero aggiunte immagini, ma sarebbe meglio ingrandire quelle presenti nella parte sull’ottimizzazione multi-obiettivo per renderle comprensibili anche stampando il testo e migliorare la disposizione delle immagini nella parte di ottimizzazione dei compositi.
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
Uno studente che non ha seguito la lezione riuscirebbe tranquillamente a preparare gli argomenti trattati in questa lezione.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
Non è necessario un intervento del docente.
Varie ed eventuali.
Nella parte della topology optimization ci sono 3 errori di battitura, nella seconda riga bisogna correggere “quel è”, nella seconda riga dopo la seconda immagine “vengono diversi” e nella quinta “ogni rigidezze”. Nella parte dell’applicazione pratica della ricerca del minimo specificherei che la stella di partenza è quella più in alto.
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
no
Il testo proposto è coerente con gli appunti personali del revisore?
si
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
.no,sono tutte presenti
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
si.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
no
Varie ed eventuali.
lavoro svolto correttamente
Spazio per eventuali note destinate al solo curatore (da non comunicarsi agli autori).
…
Ore dedicate a questa revisione
1/2 ore.