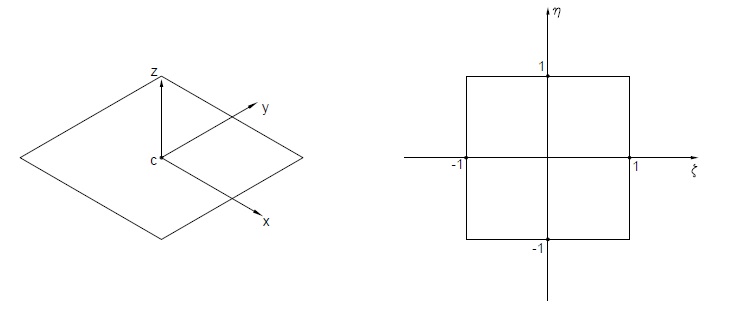Indice
Componenti di deformazione entro piano e fuori piano
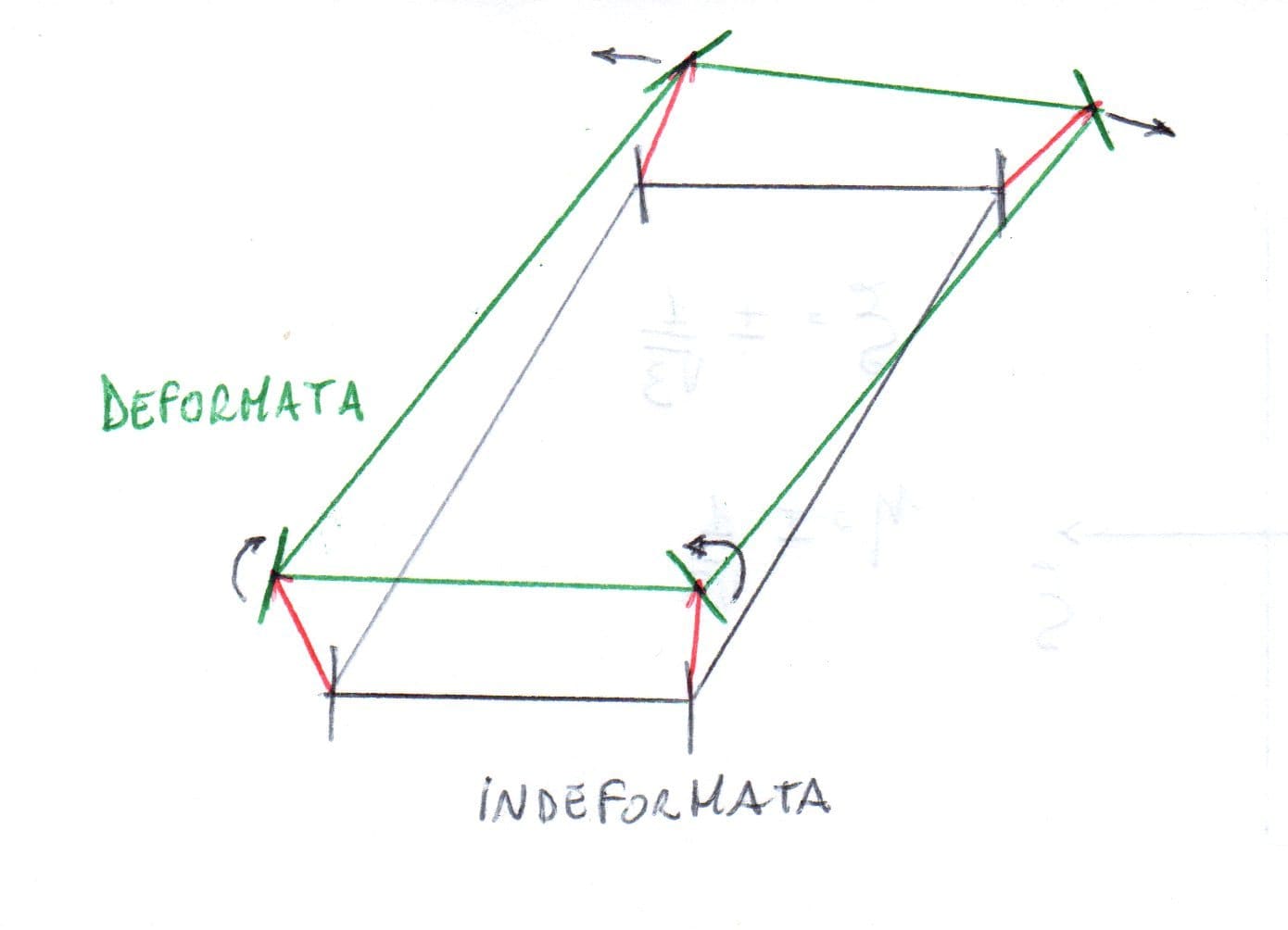
Abbiamo definito un elemento a quattro nodi, quadrilatero con quattro condizioni di forma con coordinate naturali x y z.
Utilizziamo le funzioni di forma che servono ad interpolare i valori degli spostamenti delle rotazioni dei nodi, così da ottenere spostamenti e rotazioni all' interno del volume dell' elemento.
Le informazioni sul volume dell' elemento sono descritte come informazione sul piano di riferimento, e successivamente estrapolate secondo la cinematica del segmento rigido. Quindi è sufficiente dare spostamenti e rotazioni al piano di riferimento per ricavare spostamenti e rotazioni di ogni punto entro il volume occupato dal materiale elastico per un singolo elemento.
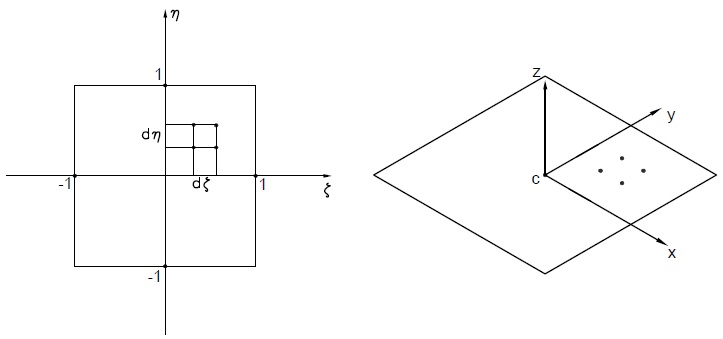
Ora rappresentiamo un sistema di riferimento locale con centro di elemento C di assi x,y,z; Parallelamente avremo un sistema di riferimento reale $\xi,\eta$ con coordinate da 1 a -1.
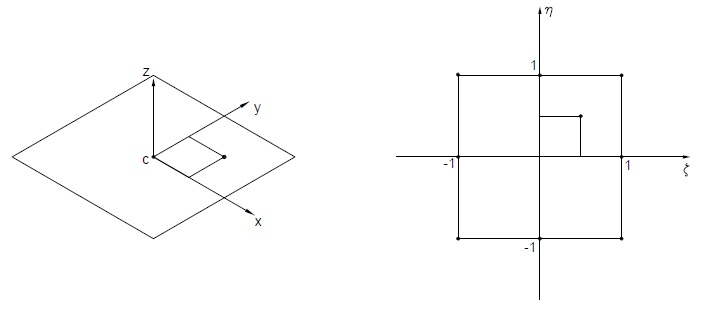
Vado a posizionare uno specifico punto con coordinate ($\xi,\eta$) del piano naturale , quindi avendo note le coordinate dei quattro nodi, possiamo trovare il punto specifico sul piano fisico di riferimento.
Noto questo punto sul piano fisico possiamo descrivere con le sue roto traslazioni, il moto di tutto il materiale rispetto al segmento rigido normale al piano che passa dal nostro punto specifico.
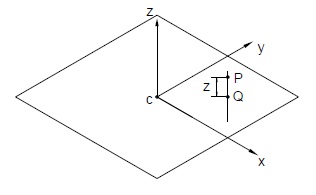
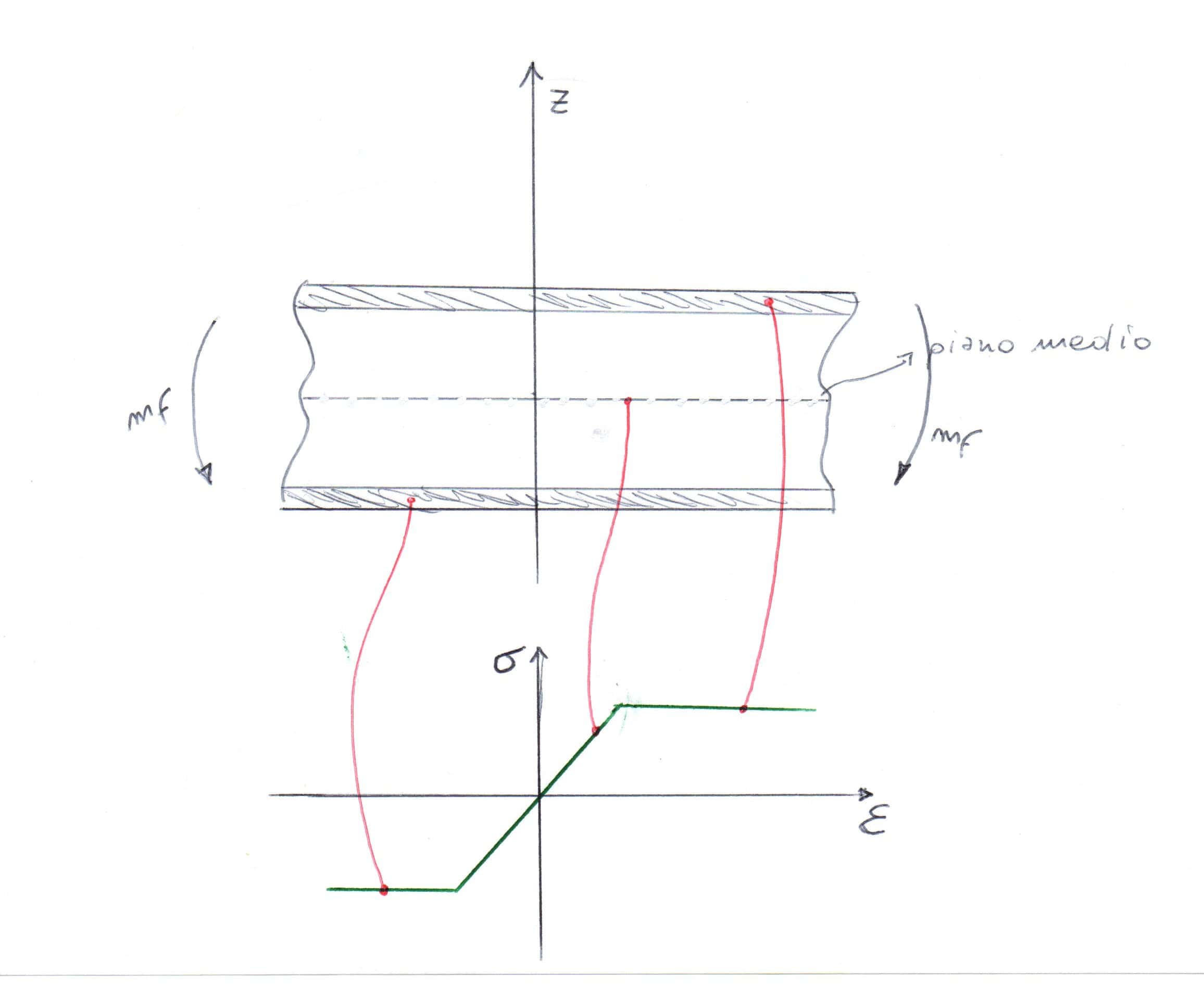
Vogliamo conoscere deformazioni per un dato punto entro il volume. Conoscendo il punto Q sul piano di riferimento ( z=0 )e il punto P fuori dal piano di riferimento sul segmento rigido a una distanza z
Possiamo definire le deformazioni come vettore composto dalle tre componenti entro piano.
$$ \underline{\epsilon}= \begin{bmatrix} \epsilon_x \\ \epsilon_y \\ \gamma_{xy} \end{bmatrix} $$
Nel punto descritto dal piano reale $\xi,\eta$ per una questione di semplicità
dalla teoria della piastra è nota la relazione:
$$ \underline{\epsilon}(\xi,\eta,z)=\underline{\bar{\epsilon}}(\xi,\eta) + z \underline{\kappa} (\xi,\eta) $$
Che ha componenti:
deformazione a piano medio in funzione di $\xi,\eta$ che è funzione dei spostamenti dei nodi in direzione x,y locali
$$ \underline{\bar{\epsilon}}= \begin{bmatrix} \bar{\epsilon}_x \\ \bar{\epsilon}_y \\ \bar{\gamma}_{xy} \end{bmatrix} $$
più la quota z per le curvature in funzione di $\xi,\eta$ , che è in funzione delle rotazioni dei nodi rispetto a x,y
$$ \underline{\kappa}= \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} $$
Poiché le componenti membranali di deformazioni sono definite sulla base degli spostamenti al piano di riferimento abbiamo
$$ \begin{bmatrix} \bar{\epsilon}_x \\ \bar{\epsilon}_y \\ \bar{\gamma}_{xy} \end{bmatrix} = \underbrace{ \begin{bmatrix} 1 && 0 && 0 && 0 \\ 0 && 0 && 0 && 1 \\ 0 && 1 && 1 && 0 \end{bmatrix} }_{\mathrm{H}^\prime} \begin{bmatrix} \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} \\ \frac{\partial v}{\partial y} \end{bmatrix} = \mathrm{H}^\prime \mathrm{Q}^\ast (\xi,\eta) \begin{bmatrix} \mathrm{u} \\ \mathrm{v} \end{bmatrix} $$
Le componenti di curvatura sono invece definite sulla base delle sole rotazioni (e non delle di $w$), da cui
$$ \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} = \underbrace{ \begin{bmatrix} 0 && 0 && +1 && 0 \\ 0 && -1 && 0 && 0 \\ -1 && 0 && 0 && +1 \end{bmatrix} }_{\mathrm{H}^{\prime\prime}} \begin{bmatrix} \frac{\partial r}{\partial x} \\ \frac{\partial r}{\partial y} \\ \frac{\partial s}{\partial x} \\ \frac{\partial s}{\partial y} \end{bmatrix} = \mathrm{H}^{\prime\prime} \mathrm{Q}^\ast (\xi,\eta) \begin{bmatrix} \mathrm{r} \\ \mathrm{s} \end{bmatrix} $$
possiamo definire per blocchi (1° blocco: 3×8, 2° blocco: 3×4, 3° blocco: 3×8) una matrice $\mathrm{B}^\prime(\xi,\eta,z)$ 3×20 di legame spostamenti - deformazioni
$$ \underline{\epsilon}(\xi,\eta,z)= \begin{bmatrix} \mathrm{H}^\prime \mathrm{Q}^\ast (\xi,\eta) & \mathrm{0} & z \; \mathrm{H}^{\prime\prime} \mathrm{Q}^\ast (\xi,\eta) \end{bmatrix} \begin{bmatrix} \mathrm{u} \\ \mathrm{v} \\ \mathrm{w} \\ \mathrm{r} \\ \mathrm{s} \end{bmatrix} $$
da cui, raccolti entro $\mathrm{d}$ vettore gradi di libertà nodali,
$$ \underline{\epsilon}(\xi,\eta,z)= \mathrm{B}^\prime(\xi,\eta,z) \mathrm{d} $$
ovvero, separando i termini di $\mathrm{B}^\prime$ in due distinte matrici in base a loro ordine in $z$
$$ \underline{\epsilon}(\xi,\eta,z)= \left( \mathrm{B}^\prime_0(\xi,\eta) + \mathrm{B}^\prime_1(\xi,\eta) z \right) \mathrm{d} $$
Facendo un passaggio analogo per le Componenti di deformazione tagliante fuori piano
Le componenti di deformazione $\gamma_{yz}$ e $\gamma_{zx}$ possono essere definite sulla base dello scostamento tra le derivate in $x,y$ dello spostamento normale al piano $w$ e le componenti di rotazione $r,s$; in particolare
$$ \gamma_{yz}= \frac{\partial w}{\partial y} - r, \quad \gamma_{zx}= \frac{\partial w}{\partial x} + s $$
da cui
$$ \begin{bmatrix} \gamma_{zx} \\ \gamma_{yz} \end{bmatrix} = \mathrm{Q} (\xi,\eta) \mathrm{w} + \begin{bmatrix} 0 & +\mathrm{N}(\xi,\eta) \\ -\mathrm{N}(\xi,\eta) & 0 \end{bmatrix} \begin{bmatrix} \mathrm{r} \\ \mathrm{s} \end{bmatrix} $$
ovvero
$$ \begin{bmatrix} \gamma_{zx} \\ \gamma_{yz} \end{bmatrix} = \underbrace{ \begin{bmatrix} \mathrm{0} & \mathrm{0} & \mathrm{Q} (\xi,\eta) & \begin{matrix} 0 \\-\mathrm{N}(\xi,\eta) \end{matrix} & \begin{matrix} \mathrm{N}(\xi,\eta) \\ 0 \end{matrix} \end{bmatrix} }_{\mathrm{B}^{\prime\prime} (\xi,\eta)} \begin{bmatrix} \mathrm{u} \\ \mathrm{v} \\ \mathrm{w} \\ \mathrm{r} \\ \mathrm{s} \end{bmatrix}= \mathrm{B}^{\prime\prime} (\xi,\eta) \; \mathrm{d} $$
con $\mathrm{B}^{\prime\prime}$ è definita per affiancamento di 5 blocchi 2×4.
Quindi in conclusione con le matrici $\mathrm{B}^{\prime}$ e $\mathrm{B}^{\prime\prime}$ è possibile definire i legami tra i gradi di libertà del elemento e le componenti deformazioni fuori piano ed entro piano.
Densità di energia elastica
$\mathrm{e}$ densità energia elastica
$$ \ e = \frac{1}{2} \, \underline{\epsilon}^{T}\, \underline{\delta} + \begin{bmatrix} \frac{1}{2} \, \underline{\gamma_{z*}}^{T} \,\underset{=}{\mathrm{D}}_{\gamma z} \gamma _{zx} \end{bmatrix} $$
La prima parte della relazione individua le componenti entro piano invece la seconda, tra le parentesi quadre, rappresenta le componenti fuori piano.
La prima parte ha come coefficienti:
- $\underline{\epsilon}^{T} $componenti entro piano di deformazione;
- $\underline{\delta} $ che è composta da $ \underset{=}{\mathrm{D}} $, matrice di legame costitutivo, per $\underline{\epsilon} $ componenti entro piano di deformazione
La seconda parte ha come coefficienti:
- $\underline{\gamma}_{z*}^{T}$ componenti fuori piano di deformazione
- $\underset{=}{\mathrm{D}}_{\gamma z} $ pezzo di legame costitutivo avete matrice con modulo di taglio
$$ \underset{=}{\mathrm{D}}_{\gamma \mathrm{z}} = \begin{bmatrix} \mathrm{G_{zx}} & 0 \\ 0 & \mathrm{G_{zy}} \end{bmatrix} $$
Avendo definito:
$$ \underline{\epsilon}= \underset{=}{{\mathrm{B}}^{\prime}} \,\underline{\mathrm{d}} $$
$$ \underline{\gamma}_{z*}^{T}= \underset{=}{{\mathrm{B}}}^{\prime\prime} \,\underline{\mathrm{d}} $$
Possiamo riscrivere la densità dell'energia elastica:
$$ \ e = \frac{1}{2} \, \underline{\mathrm{d}}^{T}\, {\underset{=}{[\mathrm{B}^{\prime}]}}^{T} \, \underset{=}{\mathrm{D}}\, \underset{=}{{\mathrm{B}}^{\prime}}\, \underline{\mathrm{d}} + \frac{1}{2} \, \underline{\mathrm{d}}^{T}\, {\underset{=}{[\mathrm{B}^{\prime\prime}]}}^{T} \, \underset{=}{{\mathrm{D}}_{\gamma z}}\, \underset{=}{{\mathrm{B}}^{\prime\prime}}\, \underline{\mathrm{d}} $$
energia potenziale elastica totale
Definiamo l'energia potenziale elastica totale come:
$$ E = \iiint_{V}\,e\, dV $$
Per integrare il volume su un dominio che è un quadrilatero nello spazio con uno spessore associato, possiamo integrare sul piano x,y con descrizione del domino complessa.
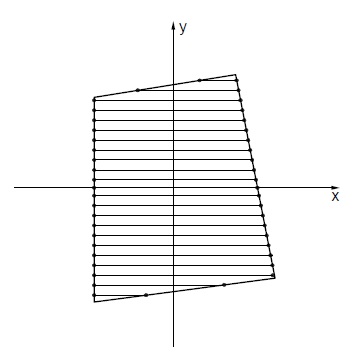
Avendo un generico quadrilatero visto dall'alto
procediamo interpolando in dx e dy lungo i seguenti segmenti
si può notare che una integrazione $\iint_{a}\,f(x,y)\, dxdy$ è molto complessa, usiamo un diverso approccio.
Ora integriamo rispetto al sistema naturale $(\xi,\eta)$
$$ \int_{-1}^{1}\int_{-1}^{1}\,f(\xi,\eta)\, d\xi,d\eta $$
Quindi possiamo ridefinire l'energia potenziale elastica totale come:
$$ E = \iiint_{V}\,e\, dV = \int_{offset-\frac{1}{2}}^{offset+\frac{1}{2}}\iint_{a} f(\xi,\eta)\, da\,dz $$
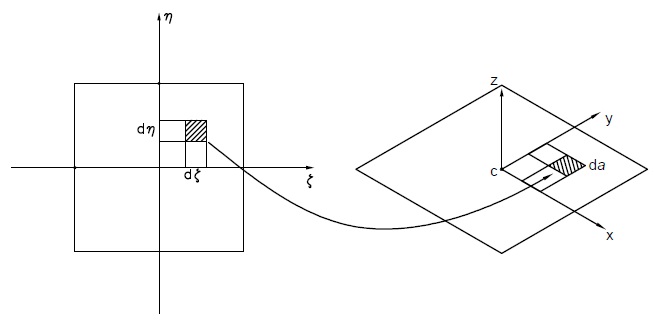
Possiamo notare che l'integrale su una dimensione fisica $da$ che non è uguale a $d\xi\,d\eta$. Prendiamo in considerazione dei contributi infinitesimi nel dominio naturale applicata all'area dimensionale $d\xi\,d\eta$
Questa aria individuata può essere riportata nel sistema fisico, considerando le coordinate dei vertici dell’aria nel dominio naturale, e trovarne le corrispettive coordinate nel dominio fisico
Trovate le coordinate fisiche dei vertici nel domino fisico, possiamo costruirci un quadrilatero o due triangoli
Ora riusiamo a calcolare l'aria del elemento infinitesimo nel piano fisico, che rappresenta l’immagine del area $d\xi\,d\eta$ sul piano naturale.
Tramite vari passaggi si può dimostrare che in questo modo l'aria $da$ è legata l'aria $d\xi\,d\eta$
$$ da \, [mm^2\,] = \,\, \begin{vmatrix} \underset{=}{J}\,(\xi,\eta) \end{vmatrix} d\xi \,d\eta $$
il termine $\begin{vmatrix} \underset{=}{J}\,(\xi,\eta) \end{vmatrix}$ indica il determinante della matrice jacobiana della trasformazione da coordinate naturali a coordinate fisiche.
Quindi avremo che:
$$ E = \int_{offset-\frac{1}{2}}^{offset+\frac{1}{2}}\int_{-1}^{1}\int_{-1}^{1}\, f(\xi,\eta)\, \begin{vmatrix} \underset{=}{J}\,(\xi,\eta) \end{vmatrix} d\xi\,d\eta $$
Quadratura gaussiana
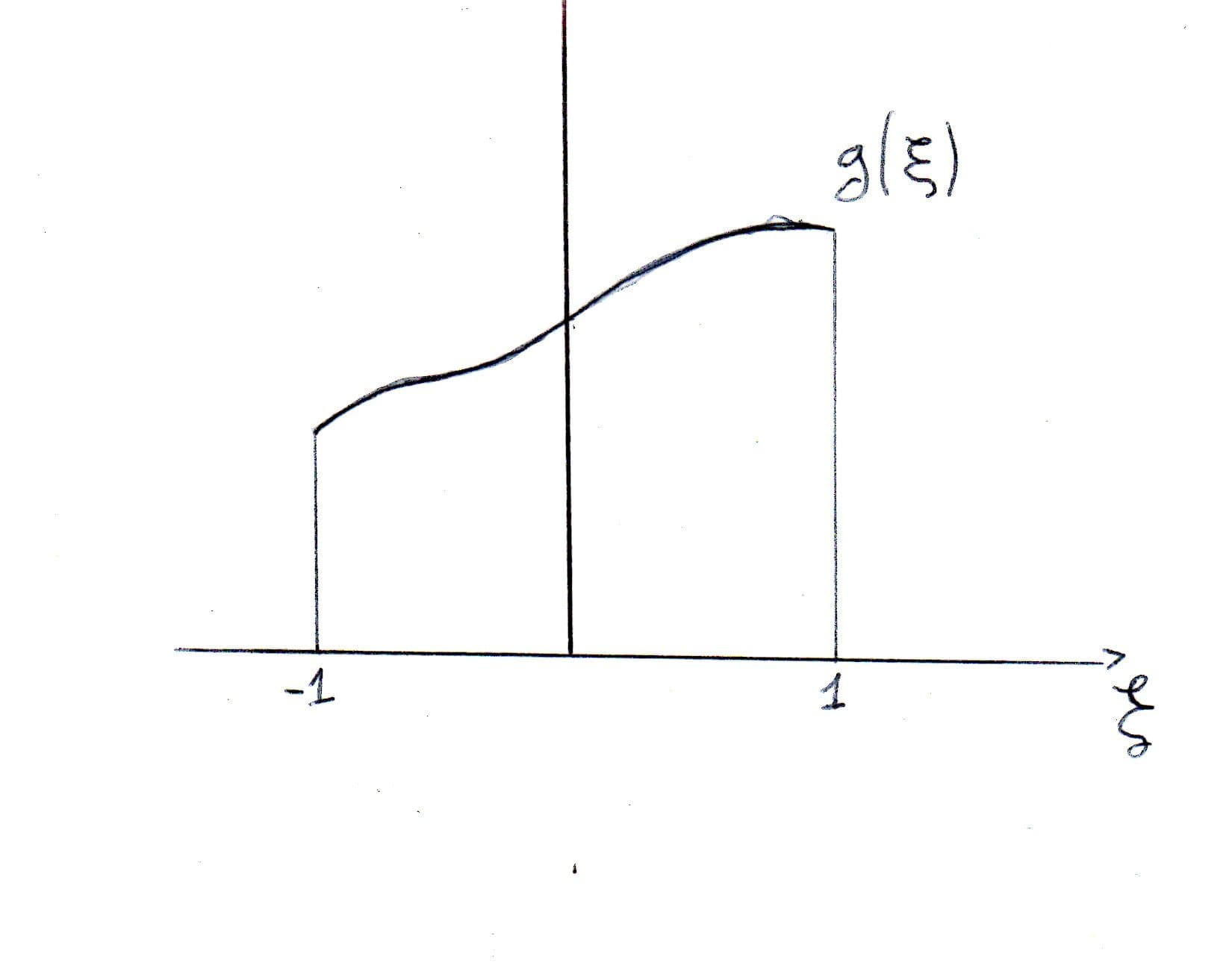
E' definita in un intervallo da -1 a 1 (unidimensionale). Ho un unico asse $\xi$ o $\eta$ (consideriamo $\xi$) e una funzione $g(\xi)$ da integrare da -1 a 1. Quindi la quadratura gaussiana definisce un metodo per approssimare l'integrale da -1 a 1 di una generica funzione $g(\xi)$. Si ammette un errore sul risultato e si rappresenta questo integrale come
$\int_{-1}^{1}g(\xi)d\xi \simeq \sum_{j=1}^{n}w_{j}g(\xi_{j})$
dove $w_{j}$ sono specifici pesi e $g(\xi_{j})$ sono valori della funzione campionata in specifici punti di campionamento. Si parla di quadratura gaussiana quando si usa uno specifico set di pesi ottimale.
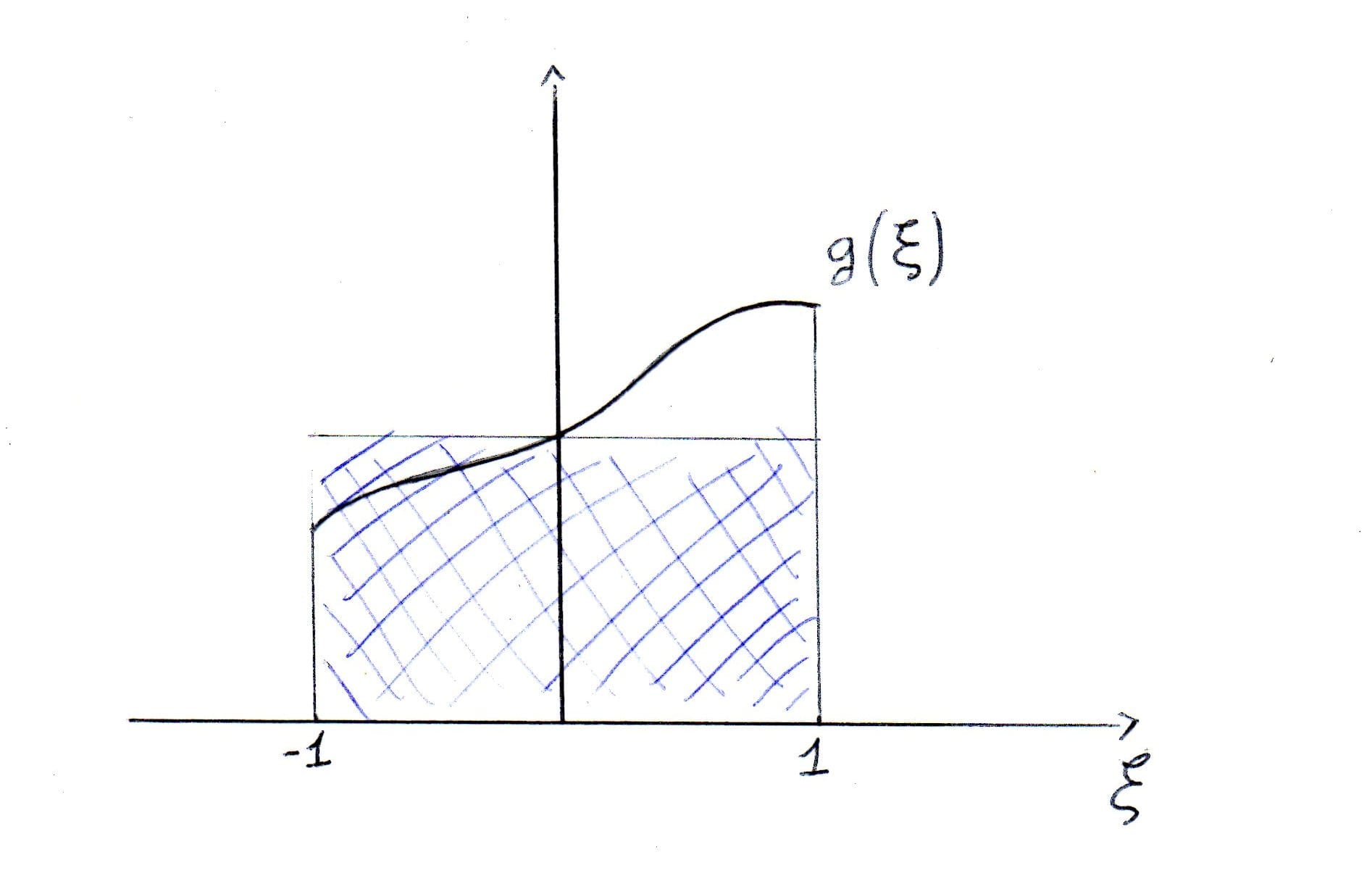
Quadratura a un punto di campionamento
Ho un solo punto di campionamento, quindi la sommatoria di cui sopra ha un solo termine. Questo punto è $\xi_{1}=0$ con $w_{1}=2$. Vul dire che approssimo l'area sottesa alla funzione con il valore campionato nell'unico punto di Gauss che è 0, moltiplicato per l'estensione totale dell'inervallo che è 2. Quindi approssimo l'area sottesa con il rettangolo così definito. Il punto $\xi_{1}$ è ottimale perchè campionando solo qui riesco a trovare l'integrale esatto di un polinomio di ordine 1. In generale i punti di Gauss sono quei punti (e quei pesi) tali per cui con n punti riesco ad integrare esattamente un polinomo di ordine $2n-1$.
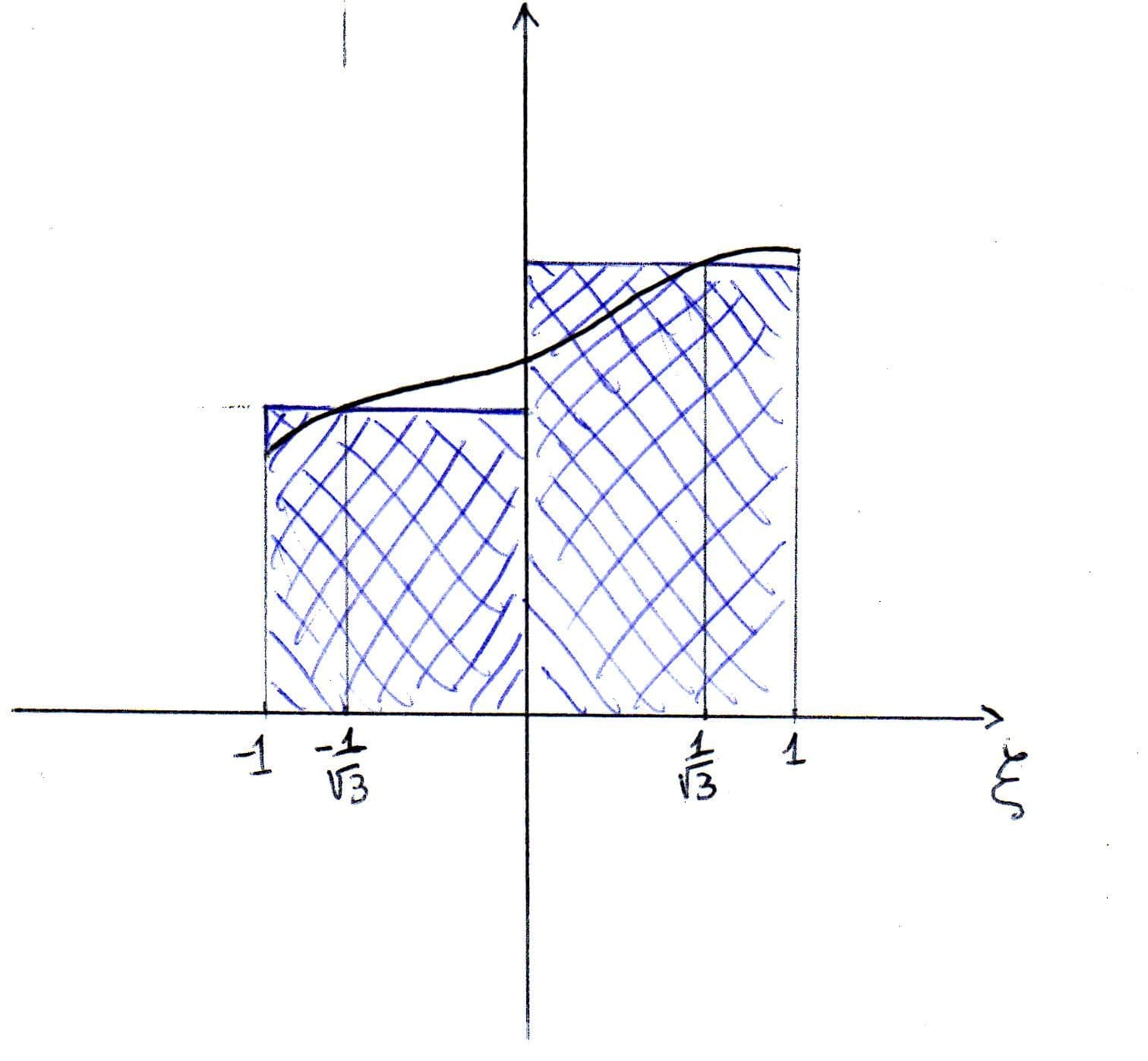
Quadratura a due punti di campionamento
I due punti sono $\xi_{1}=-\frac{1}{\sqrt{3}}$ e $\xi_{2}=+\frac{1}{\sqrt{3}}$ e i pesi associati sono $w_{1}=w_{2}=1$. Quindi approssimo l'area sottesa alla funzione con l'area sottesa ai due rettangoli di altezza pari ai valori campionati nei punti di Gauss e ampiezza 1, come in figura.
In questo modo riesco ad integrare esattamente un polinomio di ordine $2n-1=3$. Questa è la regola utilizzata tipicamente negli isoparametrici a 4 nodi quando si rappresentano elementi piastra.
Quadratura a tre punti di campionamento
I punti di campionameno sono $\xi_{1}=0$ , $\xi_{2}=+\frac{\sqrt{3}}{5}$ , $\xi_{3}=-\frac{\sqrt{3}}{5}$ e i relativi pesi sono $w_{1}=\frac{{8}}{9}$ , $w_{2}=\frac{{5}}{9}$ , $w_{3}=\frac{{5}}{9}$ .
In questo modo riesco a integrare esattamente un polinomio di ordine $2n-1=5$
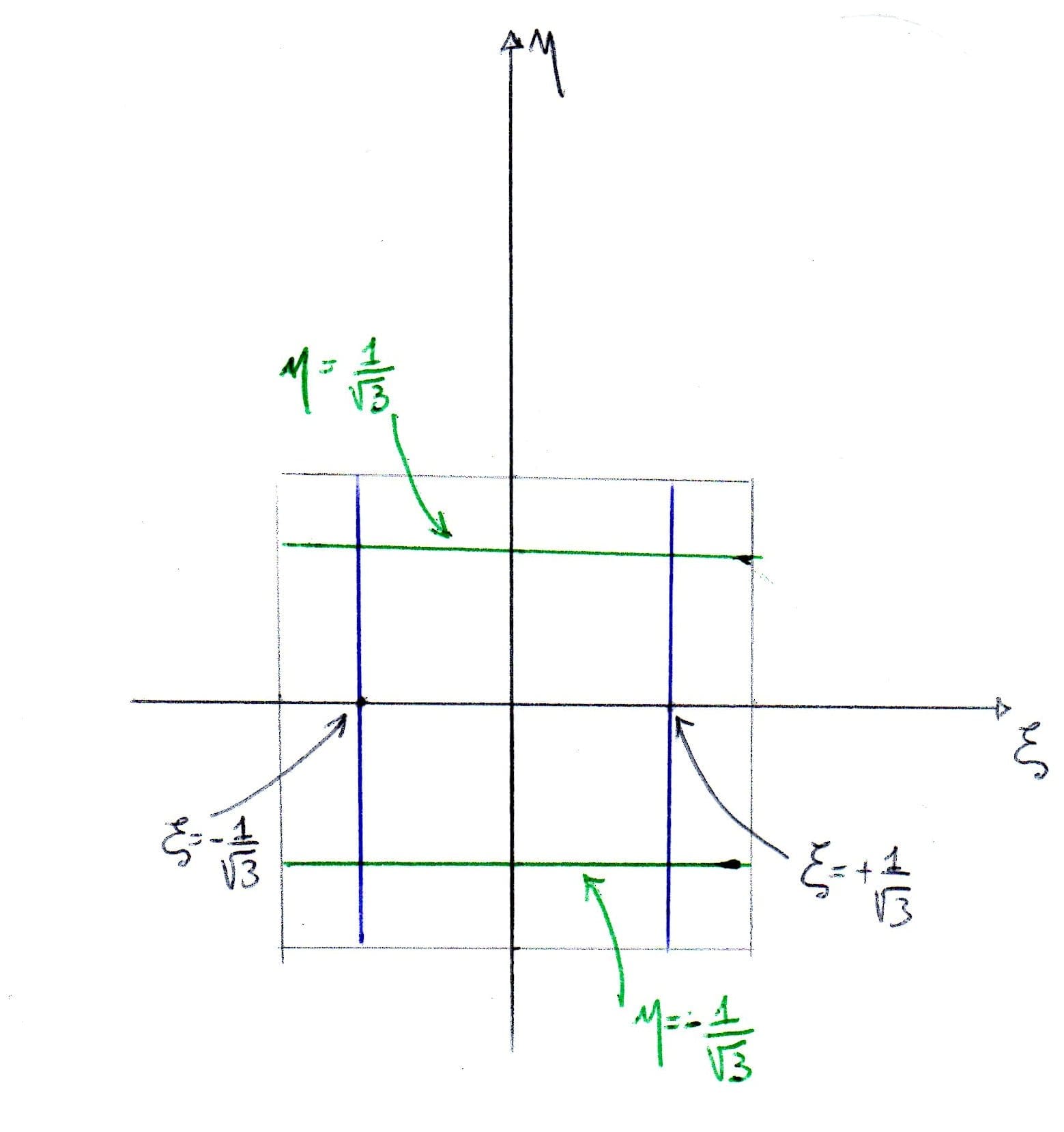
Mediante la quadratura numerica abbiamo quindi la definizione di punti di campionamento su ogni singolo asse $\xi$ ed $\eta$ del nostro quadrato elementare. Quando integro su due assi utilizzando ad esempio un campionamento a due punti, dato l'integrale
$\int_{-1}^{1}\int_{-1}^{1}f(\xi,\eta)|J(\xi,\eta)|d\xi d\eta$
Questo oggetto sarà integrato prima numericamente ad esempio lungo l'asse $\xi$, quindi per ogni valore di $\eta$ campiono la funzione nei due punti $\xi_{1}=-\frac{1}{\sqrt{3}}$ e $\xi_{2}=+\frac{1}{\sqrt{3}}$. Quando risolvo numericamente l'integrale più interno, la funzione viene campionata solamente ai punti di Gauss. Il secondo integrale, se viene svolto numericamente, prevede il campionamento di due soli valori di $\eta$ che sono $\eta_{1}=-\frac{1}{\sqrt{3}}$ e $\eta_{2}=+\frac{1}{\sqrt{3}}$. In definitiva se procedo a ricavare l'integrale con legge di quadratura gaussiana su ogni asse e due punti per asse, campiono la funzione integranda solamente in quattro punti sull'elememto.
Infatti se guardiamo il manuale dell'elemento 75 di Marc Mentat, notiamo che l'energia potenziale elastica dell'lemento è campionata solamente in questi quattro punti. I pesi in questi quattro punti sono unitari. Se uso una regola di campionamento ad un punto di Gauss per asse, rimane un solo punto di campionamento che è il centroide ($\xi=\eta=0$) e il peso è $w=4$ ($w=2$ per ogni asse). Se lavoro con tre punti per asse è un'integrazione a nove punti. Se la funzione integranda non è un polinomio di ordine $2n-1$ in $\xi$ e $\eta$, il risultato dell'integrale non è esatto. Tipicamente l'integrando non è una funzione polinomiale semplice e quindi si genera un errore nella valutazione dell'energia potenziale elastica. In realtà il risultato ottenuto con questo errore non è ingegneristicamente pessimo e quindi non avrebbe senso spendere tempo per rappresentare meglio questo integrale. Infatti per l'isoparametrico a 4 nodi si usa una regola povera (2 punti per asse) o poverissima (1 punto per asse). La funzione integranda è una funzione razionale fratta che si riduce ad un polinomio se lo Jacobiano è uniforme lungo l'elemento. Se ciò accade, l'elemento non è distorto (è un parallelepipedo) e la funzione può essere integrata esattamente mediante un polinomio di Gauss di un qualche ordine. L'elemento 75 viene definito a piena integrazione (full integration) perchè utilizza la regola di integrazione gaussiana più bassa possibile che però restituisce un risultato esatto dell'integrale nel caso l'elemento non sia distorto, ossia lo Jacobiano sia uniforme. Gli elementi a ridotta integrazione (reduced integration) sono quegli elementi che hanno un numero di punti di Gauss insufficiente per integrare in forma esatta l'energia potenziale elastica sull'elemento non distorto. Se l'elemento è distorto, l'integrazione è sempre errata ma l'errore viene coperto dall'errore di discretizzazione.
Dopo aver risolto questo integrale entro piano, potrei procedere allo stesso modo lungo lo spessore ed è conveniente farlo se il materiale è omogeneo (utilizzare almeno una regola a due punt di campionamento lungo lo spessore). Non si usa questo metodo nel caso di materiale compositi o elastoplastici. Nel caso di materiali compositi, la funzione da integrare lungo lo spessore è quadratica a tratti e quindi si scosta molto da un polinomio quadratico e quindi non è più rappresentabile con una campionatura a due punti di gauss.
Nel caso di materiali elastoplastici, se applico un momento flettente su una parete sottile può succedere che il materiale più vicino alle superfici superiore e inferiore raggiunge il carico di snervamento, mentre il materiale più interno può essere in campo lineare. In questo caso ci sarebbe disuniformità di legame costitutivo, in particolare il materiale che è andato in plasticizzazione ha un legame costitutivo a bassissima pendenza $\sigma-\epsilon$, mentre il materiale che non è andato in plasticizzazione avrà una pendenza $\sigma-\epsilon$ data dal modulo di Young. Per cui il materiale non è omogeneo del punto di vista del legame tensioni-deformazioni e quindi l'integrazione a due punti fornisce un risultato macroscopicamente sbagliato. Quindi lungo lo spessore non ci si affida più alla ottimalità dei punti di Gauss, ma si campiona a intervalli equispaziati. Se il materiale è omogeneo e elastico, o utilizzo i punti di Gauss oppure campiono a top, bottom e middle. Se il materiale è sempre omogeneo ma può snervare lungo lo spessore (elastoplastico), allora descrivo una pluralità di punti di campionamento (solitamente dispari per avere il punto al middle) per determinare la densità di energia potenziale elastica. Maggiore è il numero dei punti di campionamento, maggiore è la risoluzione con cui riesco a seguire l'avanzamento del fronte di snervamento lungo lo spessore. Nel caso di materiale composito invece, dispongo i punti per laminato: posso scegliere di mettere o un solo punto al centro del laminato oppure un numero definito di punti su ogni lamina. Il FEM restituisce i valori tensionali e deformativi ai punti di Gauss.
L'integrale sul volume dell'energia potenziale elastica vine calcolato separando i due assi entro piano dal terzo asse lungo lo spessore e, portando fuori i termini che non dipendono dal volume, si ottiene
$E=\int \int \int_{V} e dV=\frac{1}{2} d^{T}d\int \int \int_{V} \underline{B}^{T}\underline{D}\underline{B}dV$
La funzione integranda è una matrice e l'integrale rappresenta la matrice di rigidezza dell'elemento indicata con $\underline{k}$. Contiene informazioni sul legame costitutivo, sulla geometria dell'elemento. Dall'equazione tra il lavoro delle forze esterne e l'energia potenziale elastica si ricava
$\frac{1}{2} d^{T}F=\frac{1}{2} d^{T}\ \underline{k} d$
Poichè questa deve valere per ogni$d$, troviamo che, se il sistema è in equilibrio:
$F=\underline{k} d$
Consideriamo un elemento indeformato. Assegnando ad ogni nodo uno spostamento e una rotazione ottengo la configurazione deformata dell'elemento. La deformata è descritta dagli spostamenti nodali e dalle rotazioni nodali, per cui è descritta dal vettore $d$. Se non applico azioni dall'esterno questa deformata non è in equilibrio. La matrice $\underline{k}$ è quella matrice che moltiplicata per $d$, che descrive una specifica deformazione dell'elemento, mi da un vettore F che rappresenta le forze esterne. In particolare è quel vettore (composto da forze e momenti) che mantiene l'elemento in quella specifica configurazione deformata, per ogni possibile configurazione deformata. La matrice $\underline{k}$ definisce la reazione elastica dell'elemento. La matrice $\underline{k}$ di rigidezza dell'elemento è singolare e quindi non invertibile. Infatti se considero un moto di corpo rigido per un elemento traslandolo in direzione x di 1mm, ho il vettore $d=t_{x}$ diverso da 0. Ma se moltiplico $\underline{k}$ per $t_{x}$ ottengo le forze che devo applicare dall'esterno per equilibrare le reazioni elastiche associate a questo moto. Le forze necessarie per equilibrare un corpo elastico semlicemente traslato nella sua configurazone indeformata sono nulle, quindi:
$\underline{k} t_{x} = 0$
Quindi sto trasformando il vettore $t_{x}$ non nullo in un vettore nullo e le matrici non singolari questo non possono farlo. La matrice $\underline{k}$ è tante volte singolare quanti sono i moti di corpo rigido ammessi, nel caso particolare tre traslazioni e tre rotazioni.
Abbiamo detto che, per ogni $d$, l'energia potenziale elastica vale:
$E=\frac{1}{2} d^{T}\ \underline{k} d$
Nell'indeformata $d$ è uguale ad un vetture nullo. $E$ n0n può essere minore di zero perchè l'indeformata rappresenta un minimo energetico. Di conseguenza la matrice $\underline{k}$ è semi-definita positiva. La matrice di rigidezza dell'elemento serve per associare ad una configurazione deformata dell'elemento, delle azioni esterne che è necessario applicare in condizioni di equilibrio per mantenere l'elemento in quella configurazione deformata.
Supponiamo di avere una struttura composta da più elementi. Consideriamo una struttura a tetto composta da quatro elementi e nove nodi.
Esiste un unico sistema di riferimento globale O,X,Y,Z e una molteplicità di sistemi locali perchè la normale varia. Se consideriamo solo i nodi senza elementi, ad uno spostamento nodale della struttura non ho energia elastica associata e quindi non devo applicare nessun lavoro per distorcere la struttura. Quando invece inseriamo gli elementi, le deformazioni che coinvolgono i nodi associati all'elemento devono essere associate a forze applicate. Gli elementi fanno da ponte elastico tra i nodi. Ogni elemento dà un suo contributo all'energia potenziale elastica della struttura. Quando lavoro sul singolo elemento utilizzo un sistema locale x,y,z mentre quando considero tutta la struttura son costretto a lavorare nel sistema globale X,Y,Z. Quindi tutti i gradi di libertà locali dovranno essere convertiti in equivalenti globali tramite trasformazioni di coordinate. Indico con $d^{g}$ il vettore che contiene le traslazioni e le rotazioni di tutti i nodi della struttura per distinguirlo dai vettori $d$ di ogni singolo elemento. Allo stesso modo avrò le quattro matrici di rigidezza dei quattro elementi. Per ogni elemento ci sarà una mappatura tra il numero di nodi locale e il numero di nodi globale e in più ci sarà per ogni elemento una trasformazione di coordinate da sistema locale a sistema globale. Dalla corrispondenza tra le due numerazioni e dalle trasformazioni, si troverà una matrice che lega i gradi di libertà locali con quelli globali.
| Autore/Revisore | Ore |
|---|---|
| Michele Pio Granatiero | 7 |
| Pasquale Valente | 7 |
| Nicola Frisone | 7 |
| Revisore 1 | |
| Revisore 2 | |
| Revisore 3 | |
| Totale |