Analisi del gradiente delle componenti di deformazione
grafico da foro_in_lastra_infinita_v003eps.wxmx
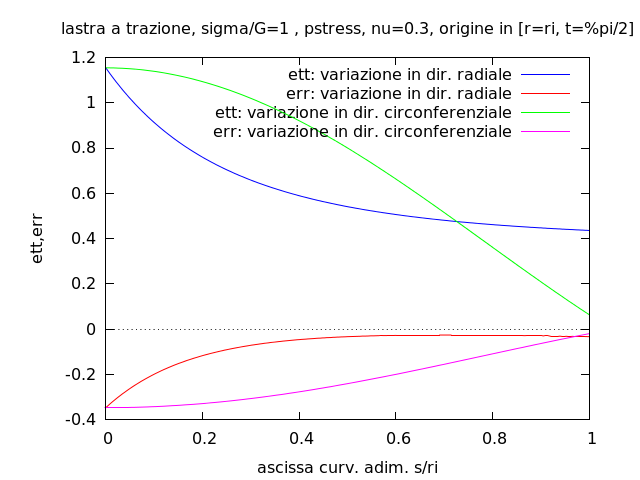
Notiamo che nel'intorno del punto in cui lo stato tensionale è massimo, $\epsilon_\theta$ è dominante, in particolare $\frac{\epsilon_\theta}{ \left | \epsilon_r \right | }=\frac{1}{\nu} \approx 3.3$.
Risulta inoltre che $\epsilon_\theta$ ha derivata direzionale nulla in direzione circonferenziale, mentre ha derivata direzionale rilevante in direzione radiale.
Un elemento isoparametrico 4 nodi a ridotta distorsione (es. trapezio rettangolo con ridotto scarto tra le basi e tra basi e altezza, diciamo quasi quadrato) riesce a rappresentare mediante una deformazione trapezia un campo di deformazioni con componente circonferenziale lineare in $r$ ma solo costante in $\theta$.
Tale comportamento permette quindi ad una mesh di elementi isoparametrici 4 nodi di rappresentare la componente di deformazione dominante con un andamento lineare a tratti nella direzione in cui la variazione della stessa è più rapida (massima derivata direzionale).
La natura costante a tratti delle componenti di deformazione normalmente associata agli elementi a campo di spostamenti lineare / bilineare caratterizza nell'isoparametrico 4 nodi
- l'andamento della componente di deformazione non dominante $\epsilon_r$ nella direzione di massima derivata direzionale
- l'andamento della componente di deformazione dominante $\epsilon_\theta$ nella direzione in cui la derivata direzionale è nulla o quantomento limitata.
Nel caso dell'elemento triangolare 3 nodi lo stato deformativo è invece strettamente costante a tratti, e in ogni direzione.
Tale coincidenza tra direzione preferenziale per la rappresentazione della tensione circonferenziale propria dell'elemento iso4 e l'effettiva rapida variazione della stessa nella soluzione esatta rende l'elemento is4 nettamente superiore al triangolare CST nella rappresentazione dello stato tensionale nell'intorno degli intagli.